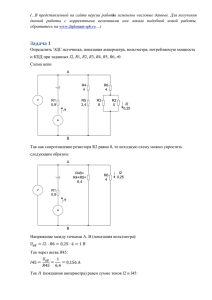
КУРСОВАЯ РАБОТА по предмету: Теория телетрафика
реклама
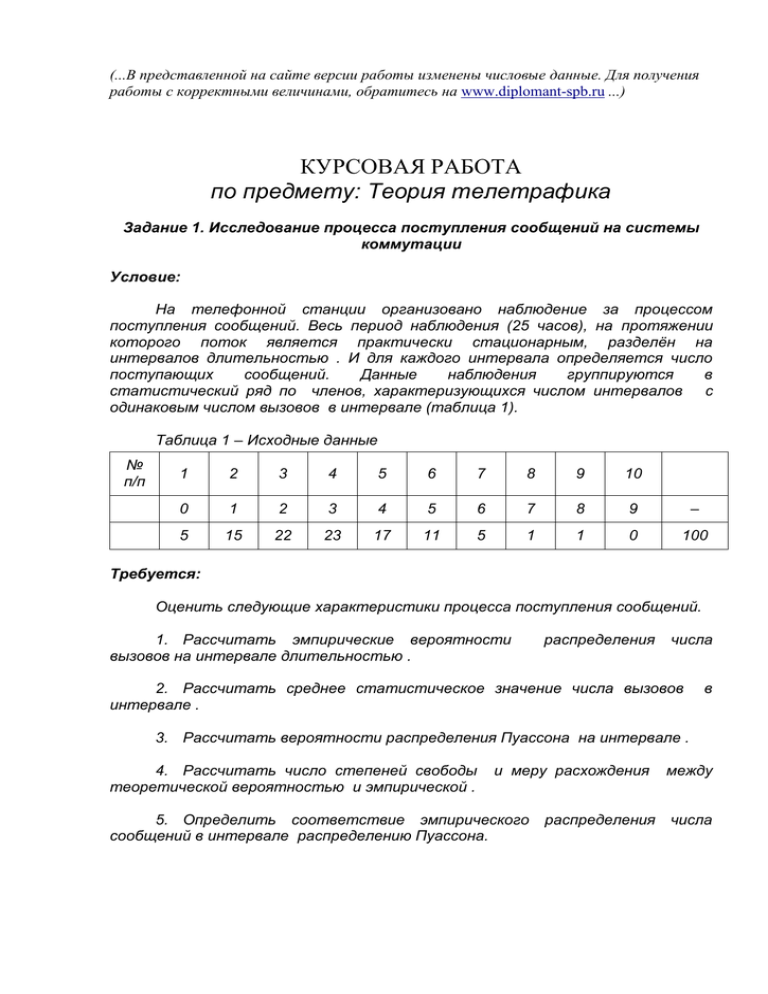
(...В представленной на сайте версии работы изменены числовые данные. Для получения
работы с корректными величинами, обратитесь на www.diplomant-spb.ru ...)
КУРСОВАЯ РАБОТА
по предмету: Теория телетрафика
Задание 1. Исследование процесса поступления сообщений на системы
коммутации
Условие:
На телефонной станции организовано наблюдение за процессом
поступления сообщений. Весь период наблюдения (25 часов), на протяжении
которого поток является практически стационарным, разделён на
интервалов длительностью . И для каждого интервала определяется число
поступающих
сообщений.
Данные
наблюдения
группируются
в
статистический ряд по членов, характеризующихся числом интервалов с
одинаковым числом вызовов в интервале (таблица 1).
Таблица 1 – Исходные данные
№
п/п
1
2
3
4
5
6
7
8
9
10
0
1
2
3
4
5
6
7
8
9
–
5
15
22
23
17
11
5
1
1
0
100
Требуется:
Оценить следующие характеристики процесса поступления сообщений.
1. Рассчитать эмпирические вероятности
вызовов на интервале длительностью .
распределения
числа
2. Рассчитать среднее статистическое значение числа вызовов
интервале .
в
3. Рассчитать вероятности распределения Пуассона на интервале .
4. Рассчитать число степеней свободы
теоретической вероятностью и эмпирической .
и меру расхождения
5. Определить соответствие эмпирического
сообщений в интервале распределению Пуассона.
между
распределения числа
(...В представленной на сайте версии работы изменены числовые данные. Для получения
работы с корректными величинами, обратитесь на www.diplomant-spb.ru ...)
Решение:
Рассчитаем эмпирические вероятности распределения числа вызовов на
заданном интервале по формуле:
[1]
Результаты расчётов эмпирических вероятностей приведены в таблице 1.
Таблица 1 – Результаты расчётов эмпирических вероятностей
№
п/п
Сумма
1
1
1
1
1
1
1
1
1
11
1
1
1
1
1
1
1
1
1
1
–
1
11
11
11
11
11
1
1
1
1
111
1,11
1,11
1,11
1,11
1,11
1,11
1,11
1,11
1,11
1
1
Рассчитаем среднее статистическое значение числа вызовов
заданном интервале:
в
[1]
Рассчитаем вероятности
интервале по формуле:
распределения
Пуассона
на
заданном
[1]
Результаты
расчётов
приведены в таблице 1.
вероятностей
распределения
Пуассона
Таблица 1 – Результаты расчётов вероятностей распределения
Пуассона
№
п/п
1
1
1
1
1
1
1
1
1
11
Сумма
(...В представленной на сайте версии работы изменены числовые данные. Для получения
работы с корректными величинами, обратитесь на www.diplomant-spb.ru ...)
1,111 1,111 1,111 1,111 1,111 1,111 1,111 1,11 1,111 1,111
1
Рассчитаем меру расхождения между теоретической вероятностью и
эмпирической по формуле:
[1]
Таблица 1 – Расчёт меры расхождения
№ п/п
1
1
1
1
1
1
1
1
1
11
1,11
1,11
1,11
1,11
1,11
1,11
1,11
1,11
1,11
1
1,11
1
1,11
1
1,111
1,11
1
1,11
1
1,111
1,11
1
1,11
1,11
1
1,111
11,1
11,1
111,1
1
111,
1
11,1
1
1111,
1
PP 10
2
k
k
P
k
6
11,1
111
1
111
1111
1
X1=
6
100
(76.9
58.8
215.86
160.7
96.39
1469.
83.3
5000
500
200
10
2.
Рассчитать число степеней свободы по формуле:
[1]
где – число независимых условий, налагаемых на вероятности , и
определению вероятности
того, что величина, имеющая
распределение
с
степенями свободы, превзойдёт данное
значение . В данном случае .
По значениям и определяем вероятность того, что величина, имеющая
распределение с степенями свободы, превзойдёт данное значение. Значениям
и соответствует вероятность
(...В представленной на сайте версии работы изменены числовые данные. Для получения
работы с корректными величинами, обратитесь на www.diplomant-spb.ru ...)
Задание 3. Оценка пропускной способности управляющих устройств
систем коммутации
Условие:
Ступень группового искания координатной АТС с индивидуальными
управляющими устройствами (маркерами) для каждого блока комплектуется
из S коммутационных блоков. Средняя длительность занятия входа ступени
ГИ – tвх. На ступень искания поступает нагрузка yвх . Управляющие устройства
работают по системе с ожиданием. Средняя длительность занятия одним
вызовом управляющего устройства – h , допустимое время ожидания – tдоп.
Требуется:
1. Определить следующие качественные показатели работы управляющих
устройств ступени искания при постоянной и экспоненциально распределенной
длительности обслуживания:
- вероятность ожидания для поступившего вызова – P{ >0};
- вероятность ожидания свыше допустимого времени t для любого
поступившего вызова - P{ >t} при фиксированных значениях tдоп.
- вероятность ожидания свыше допустимого времени t для задержанного
вызова - P{з>t} при фиксированных значениях tдоп.
- среднее время ожидания для любого поступившего вызова и задержанного
вызова з
2. Определить среднее число ожидающих вызовов j при экспоненциально
распределенной длительности обслуживания.
3. По результатам расчетов построить графические зависимости:
- вероятности P{ >t} от величины t при удельной поступающей нагрузке на
управляющее устройство c для постоянной и экспоненциально распределенной
длительности обслуживания P{ >t}= f (t) при V=1, c = const;
- вероятности P{з >t} от величины t при поступающей нагрузке на
управляющее устройство c для постоянной и экспоненциально распределенной
длительности обслуживания P{з>t}= f (t) при V=1, c = const;
(...В представленной на сайте версии работы изменены числовые данные. Для получения
работы с корректными величинами, обратитесь на www.diplomant-spb.ru ...)
4. Определить изменения (в процентах) качественных показателей
обслуживания {>t}для фиксированных значений tдоп при постоянной и
экспоненциально распределенной длительности обслуживания, если нагрузка
на ступень искания увеличится на 5%.
Исходные данные :
S=2
tвх = 64 c
yвх = 32 Эрл
h = 0,54 с
tдоп1 = 0,81 с
tдоп2 = 1,08 с
tдоп3 =1,62 с
Решение.
1. Определим нагрузку, поступающую на входы одного блока ГИ по формуле:
yбл = yвх / S
32
убл= 2 16 Эрл
Определим расчетное значение:
.674
yp
yр.бл = yp 0
ур бл =
16
0
.
674
16
18
.
7
Эрл
Определим Удельную расчетную нагрузку :
cр = h * yр.бл / tвх
ср= 1,11 * 11,1 / 11 = 1,11 Эрл
Для однолинейного пучка (V=1) всегда P{ >1}= cр = 1,11 Эрл
( - длительность ожидания начала обслуживания)
Определение P{ > t} для экспоненциально распределенной длительности
обслуживания выполняют с помощью функции Эрланга.
(...В представленной на сайте версии работы изменены числовые данные. Для получения
работы с корректными величинами, обратитесь на www.diplomant-spb.ru ...)
При V=1 и, принимая y = cр = 1,11 Эрл, получаем из (1) :
P{ >t} = cр * e - (1- Cр) t, где t = tдоп / h ;
Тогда
при t1 = tдоп1 / h = 1,11 / 1,11 = 1,1
при t1 = tдоп1 / h = 1,11 / 1,11 = 1
при t1 = tдоп1 / h = 1,11 / 1,11 = 1
-
P{ > t1} = cр * e - (1- Cр) t1 = 1,111
P{ > t1} = cр * e - (1- Cр) t1 = 1,11
P{ > t1} = cр * e - (1- Cр) t1 = 1,111
Определение P{ > t}для постоянной длительности обслуживания выполняют
при помощи кривых Кроммелина.
При V=1 и, принимая ал = cр = 1,11 Эрл – (среднее использование одной линии),
находим из кривых Кроммелина :
при t1 = 1,1
при t1 = 1
при t1 = 1
-
P{ > t1} = 1,111
P{ > t1} = 1,111
P{ > t1} = 1
Определяем вероятности P{з > t}по соотношению :
P{з > t} = P{ > t} / cр
- для экспоненциально распределенной длительности обслуживания :
P{з > t1} = P{ > t1} / cр = 1,111 / 1,11 = 1,11
P{з > t1} = P{ > t1} / cр = 1,11 / 1,11 = 1,11
P{з > t1} = P{ > t1} / cр = 1,111 / 1,11 = 1,111
- для постоянной длительности обслуживания :
P{з > t1} = P{ > t1} / cр = 1,111 / 1,11 = 1,111
P{з > t1} = P{ > t1} / cр = 1,111 / 1,11 = 1,111
P{з > t1} = P{ > t1} / cр = 1/ 1,11 = 1
Определим среднее время ожидания для любого поступившего вызова
задержанного вызова з.
- для экспоненциально распределенной длительности обслуживания :
и
(...В представленной на сайте версии работы изменены числовые данные. Для получения
работы с корректными величинами, обратитесь на www.diplomant-spb.ru ...)
0
P
c
p
1
и 3 1cp
1
c
p
1
c
h
.16
0
0
.19
1
0
.16
3
1
1
.19
1
0
.16
- для постоянной длительности обслуживания :
c
P
0
2
(
1
c
) 2
(
1
c
)и
p
h
1
2(1cp)
3
p
0
.
16
1
0
.
095
0
.
59
2
(
1
0
.
16
)
2
(
1
0
.
16
)
3
1. Определим среднее число ожидающих вызовов j при экспоненциально
распределенной длительности обслуживания как :
j = P{ >1}* cр / (1 - cр ) = cр1 / (1 - cр )
j = 1,111 / 1,11 = 1,11
1. Графики P{ >t}= f (t) при V=1, c = const и P{з>t}= f (t) при V=1, c = const
приведены на рисунках 1 и 1.
1. Определим изменения качественных показателей P{ >t}для 1-х значений tдоп
при
постоянной
и
экспоненциально
распределенной
длительности
обслуживания, если нагрузка на ступень искания увеличится на 1% и составит
y /вх = 1,11 * 11 = 11,1 Эрл.
При этом : y /бл = y /вх / S = y /вх = 11,1 Эрл
y /р.бл = 11,1 Эрл
c /р = h * y /р.бл / tвх = 1,11 * 11,1 / 11 = 1,11 Эрл
- для экспоненциально распределенной длительности обслуживания :
при t1 = tдоп1 / h = 1,11 / 1,11 = 1,1
при t1 = tдоп1 / h = 1,11 / 1,11 = 1
при t1 = tдоп1 / h = 1,11 / 1,11 = 1
Изменения составляют :
-
P /{ > t1} = c /р * e - (1- C ` р) t1 = 1,111
P /{ > t1} = c /р * e - (1- C ` р) t1 = 1,111
P /{ > t1} = c /р * e - (1- C ` р) t1 = 1,111
(...В представленной на сайте версии работы изменены числовые данные. Для получения
работы с корректными величинами, обратитесь на www.diplomant-spb.ru ...)
при t1 = 1,1
при t1 = 1
при t1 = 1
-
( 1,111 - 1,111) / 1,111 = 1,111 = 1,1 %
( 1,111 - 1,11) / 1,11 = 1,111 = 1,1 %
( 1,111 - 1,111) / 1,111 = 1,111 = 1,1 %
При постоянной длительности обслуживания определить изменения качества
при изменении значения cр от
до не представляется возможным, так как
кривые Кроммелина заданы через дискретные значения 1,1 Эрл.
P{y>t}
0,05
0,045
0,04
0,035
0,03
0,025
0,02
0,015
0,01
0,005
0
эксп
пост
t
1,5
2
Рис.1
3
(...В представленной на сайте версии работы изменены числовые данные. Для получения
работы с корректными величинами, обратитесь на www.diplomant-spb.ru ...)
P{y3 >t}
0,3
0,25
эксп
0,2
0,15
0,1
пост
0,05
0
t
1,5
2
3
Рис.2
(...В представленной на сайте версии работы изменены числовые данные. Для получения
работы с корректными величинами, обратитесь на www.diplomant-spb.ru ...)
ЛИТЕРАТУРА
1
Мамонова Н. П. «Теория телетрафика: методические
рекомендации к изучению дисциплины. Заочное обучение» –
СПб.: СПбГУТ, 2002.
2
Лившиц Б. С., Пшеничников А. П., Харкевич А. Д. «Теория
телетрафика. Учебник для ВУЗов» – М.: Связь, 1979.