Контрольные работы по теории вероятности и математической статистике. СОДЕРЖАНИЕ

(...В представленной на сайте версии работы изменены числовые данные. Для получения
работы с корректными величинами, обратитесь на www.diplomant-spb.ru ...)
Контрольные работы по теории вероятности и математической
статистике.
СОДЕРЖАНИЕ
?. ТЕОРИЯ ВЕРОЯТНОСТЕЙ ........................................................................... ?
?.?. Задача ?. ............................................................................................................................... ?
?.?. Задача ?. ............................................................................................................................... ?
?.?. Задача ?. ............................................................................................................................... ?
?.?. Задача ?. ............................................................................................................................... 7
?. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА. .................................................... ??
?. СЕТЕВОЕ ПЛАНИРОВАНИЕ. .................................................................... ??
?. ВЫПУСК ПРОДУКЦИИ ПРИ НЕОПРЕДЕЛЕННОМ СПРОСЕ. ....... ??
?. ЗАДАЧА О КОНКУРИРУЮЩИХ СУПЕРМАРКЕТАХ. ....................... ??
2
(...В представленной на сайте версии работы изменены числовые данные. Для получения
работы с корректными величинами, обратитесь на www.diplomant-spb.ru ...)
?. ТЕОРИЯ ВЕРОЯТНОСТЕЙ
?.?. Задача ?.
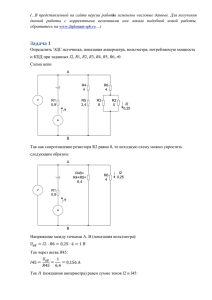
Покупатель может приобрести акции трех компаний. Надежность
первой компании в течении года оценивается экспертами на уровне a%,
второй – на уровне b%, третьей – на уровне с%. Чему равна вероятность того,
что: а) все компании в течении года не станут банкротами; б) наступит хотя
бы одно банкротство. Решить задачу при следующих данных: а=8?, b=88,
с=9?.
Решение.
Обозначим события:
А – первая компания в течении года не станет банкротом,
В – вторая компания в течении года не станет банкротом,
С – третья компания в течении года не станет банкротом.
По условию задачи вероятности этих событий равны:
Р(А) = ?.8?, Р(А) = ?.88, Р(А) = ?.9?
1.
Событие D, состоящее в том, что все три компании года не станут
банкротами, произойдет в том случае, если произойдут все три события: А,
В, С. Это значит что событие D равно:
D=A*B*C
Т.к. события А, В, С являются независимыми, то по теореме
умножения
вероятностей
вероятность
произведения
событий
равна
произведению вероятностей:
P(D) = P(A) * P(B) * P(C)
P(D) = ?.8? * ?.88 * ?.9? = ?.7?89?
Вероятность того, что все компании в течении года не станут
банкротами, равна ?.7?89?.
3
(...В представленной на сайте версии работы изменены числовые данные. Для получения
работы с корректными величинами, обратитесь на www.diplomant-spb.ru ...)
?. Пусть Е – событие, состоящее в том, что наступит хотя бы одно
банкротство. Противоположное событие состоит в том, что все компании не
станут банкротами, т.е.
ED
Поскольку сумма вероятностей противоположных событий равна ?, то
P
(
E
)

1

P
(
E
)

1

P
(
D
)

1

0
.
71896

0
.
28104
Вероятность того, что наступит хотя бы одно банкротство =
?.?8???
?.?. Задача ?.
Вероятность того, что новый товар будет пользоваться спросом на
рынке, если конкурент не выпустит в продажу аналогичный продукт, равна
р?. Вероятность того, что товар будет пользоваться спросом при наличии на
рынке
конкурирующего
товара,
равна
р?.
Вероятность
того,
что
конкурирующая фирма выпустит аналогичный товар на рынок, равна q. Чему
равна вероятность того, что товар будет иметь успех? Решить задачу при
следующих данных: р? = ?.7?, р? = ?.??, q = ?.??.
Решение:
Обозначим события:
А – событие, состоящее в том, что товар будет иметь успех;
Н? – событие, состоящее в том, что не выпустит в продажу
аналогичный продукт;
Н? - событие, состоящее в том, что выпустит в продажу аналогичный
продукт.
По условию задачи известны условные вероятности:
A
P( )0.75
H
1
A
P( )0.42
H
2
4
(...В представленной на сайте версии работы изменены числовые данные. Для получения
работы с корректными величинами, обратитесь на www.diplomant-spb.ru ...)
События Н? и Н? являются несовместимыми и образуют полную
группу, поэтому сумма вероятностей этих событий равна единице:
Р(Н?) + Р(Н?) = ?
Отсюда следует, что:
Р(Н?) = ? – Р(Н?) = ? – ?.?? = ?.??
Для определения вероятности события А применим формулу полной
вероятности:
A
A
P(A)

P(
)
*
P(
)

P(
)
*
P(
)
H
H
1
2
H
H
1
2
Подставляя числовые значения, получим:
Р(А) = ?.?? * ?.7? + ?.?? * ?.?? = ?.???
Вероятность того, что товар будет иметь успех, равна ?.???.
?.?. Задача ?.
В ходе аудиторской проверки строительной компании, аудитор
случайным образом собирает n счетов. Известно, что а% счетов содержат
ошибки. Требуется:
 Составить таблицу распределения вероятностей правильных
счетов;
 Найти числовые характеристики этого распределения;
 Записать функцию распределения вероятностей и построить ее
график;
 Определить вероятность того, что хотя бы один счет будет с
ошибкой.
Решить задачу для следующих данных: n = ?, а = ??.
Решение:
5
(...В представленной на сайте версии работы изменены числовые данные. Для получения
работы с корректными величинами, обратитесь на www.diplomant-spb.ru ...)
Число правильных счетов есть случайная величина Х, которая может
принимать значения: ?, ?, ?, ?, ?, ?. Вероятности этих событий определяются
по формуле Бернулли: pn(m) = Cnm * pm * qn-m, где q = ?.?? – вероятность
неправильного счета, р = ? – q = ? – ?.?? = ?.?9 – вероятность правильного
счета. Получим:
0
0
5
P(X

0)

(0)

*
*

0
.
0029
p
C
0.69
0.31
5
5
1
1
4
P(X

1)

(1)

*
*

0
.
0319
p
C
0.69
0.31
4
4
2
2
3
P(X

2)

(2)

*
*

0
.
1418
p
C
0.69
0.31
3
5
3
3
2
P(X

3)

(3)

*
*

0
.
3157
p
C
0.69
0.31
5
5
4
4
1
P(X

4)

(4)

*
*

0
.
3513
p
C
0.69
0.31
5
5
5
5
0
P(X

5)

(5)

*
*

0
.
1564
p
C
0.69
0.31
5
5
Сделаем проверку:
?.???9 + ?.???9 + ?.???8 + ?.???7 + ?.???? + ?.???? = ?
Распределение вероятностей случайной величины Х содержится в
следующей таблице:
X
P
?
?
?
?
?,???9 ?,???9 ?,???8 ?,???7
?
?,????
?
?,????
Математическое ожидание дискретной случайной величины Х находим
по формуле:
n
M
(
X
)
p
x
i*
i
i
1
Где xi – возможные значения Х; pi – соответствующие вероятности.
М(Х) = ? * ?.???9 + ? * ?.???9 + ? * ?.???9 + ? * ?.???7 + ? * ?.???? + ? *
?.???? = ?.??
Дисперсию случайной величины Х находим по формуле:
D(X) = M(X?) – (M(X))?.
6
(...В представленной на сайте версии работы изменены числовые данные. Для получения
работы с корректными величинами, обратитесь на www.diplomant-spb.ru ...)
Т.к. М(Х?) = ? * ?.???9 + ? * ?.???9 + ? * ?.???9 + 9 * ?.???7 + ?? * ?.???? +
?? * ?.???? = ??.97?
Тогда
D(X) = ??.97? – ?.??? = ??.97? – ??.9??? = ?.??9?
Среднее квадратичное отклонении случайной величины Х равно:

(
X
)

D
(
X
)

1
.
0695

1
.
0341
Найдем функцию распределения вероятностей F(x).
Если х ≤ ?, то F(x) = ?
Если ? < х ≤ ?, то F(x) = ?.???9
Если ? < х ≤ ?, то F(x) = ?.???7
Если ? < х ≤ ?, то F(x) = ?.?7??
Если ? < х ≤ ?, то F(x) = ?.?9??
Если ? < х ≤ ?, то F(x) = ?.8???
Если х > ? , то F(x) = ?.8??? + ?.???? = ?
Событие А, состоящее в том, что хотя бы один счет будет с ошибкой,
является противоположным к событию, что все счета будут правильными,
следовательно:
Р(А) = ? – Р(Х=?) = ? – ?.???? = ?.8???
График функции f(x) изображен на рисунке ?.
7
(...В представленной на сайте версии работы изменены числовые данные. Для получения
работы с корректными величинами, обратитесь на www.diplomant-spb.ru ...)
1,2000
1,0000
0,8436
y=F(x)
0,8000
0,6000
0,4923
0,4000
0,2000
0,0029
0,0000
0
0,1766
0,0347
1
2
3
4
5
x
Рис ?. – График функции y=F(x)
Вероятность того, что хотя бы один счет будет с ошибкой, равна
?.8???.
?.?. Задача ?.
Годовой выпуск продукции мебельной фабрики приблизительно
распределен по нормальному закону со средним значением, равным m
тыс.ед. продукции, и стандартным отклонением σ тыс.ед. Найти вероятность
того, что годовой выпуск продукции :
 Окажется ниже b тыс.ед.
 Превысит а тыс.ед.
Решить задачу для следующих данных: m = ??8, s = ?7, b = 9?, a = ???.
Решение:
Обозначим через Х – годовой выпуск продукции мебельной фабрики.
Это непрерывная случайная величина, имеющая нормальное распределение с
параметрами m и σ. Поэтому вероятность попадания случайной величины в
промежуток [a,b] вычисляется по формуле:
8
(...В представленной на сайте версии работы изменены числовые данные. Для получения
работы с корректными величинами, обратитесь на www.diplomant-spb.ru ...)
b
m
a
m
P
(
a

X

b
)

Ô(
)

Ô(
),


Где
2
1 t
Ô(x)
 edt
- функция Лапласа.
2

x
2


Вероятность того, что годовой выпуск продукции окажется ниже b = 9?
тыс.ед.:
96
118

118
P
(


X

96
)

Ô(
)

Ô(
)

Ô(-1
0

0
.
09
17
17


118
151
118
P
(
151

X


)

Ô(
)

Ô(
)

1
Ô(1.9

17
17
1

0
.
9739

0
.
0261
Таким образом, с меньшей вероятностью, годовой выпуск продукции
будет находиться между 9? и ??? тыс.ед.
Расчет в Excel представлен на рисунках ниже:
9
(...В представленной на сайте версии работы изменены числовые данные. Для получения
работы с корректными величинами, обратитесь на www.diplomant-spb.ru ...)
Рис ? – Лист Excel в табличном режиме
10
(...В представленной на сайте версии работы изменены числовые данные. Для получения
работы с корректными величинами, обратитесь на www.diplomant-spb.ru ...)
Рис ? – Лист Excel в режиме проверки формул.
?. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА.
Имеются статистические данные об объемах лесных грузов, в
тыс.куб.м.,
перевозимых
еженедельно
от
лесозаготовительных
к
деревообрабатывющим предприятиям: {xi}i=?.n.
Требуется
произвести
первичную
обработку
данных
методами
математической статистики. Для этого необходимо:
 Составить статистический ряд;
 Для каждого частичного интервала определить частоты, относительные
частоты, накопленные частоты, накопленные относительные частоты;
 Построить полигоны, кумуляты и гистограмму;
 Определить
выборочные
характеристики
статистического
распределения.
Решить задачу для следующих статистических данных:
??
??
??
?8
??
??7
??
??
?8?
??
??
??8
87
?8?
??
98
??
??
??
?7?
?8
?7?
??
???
??
???
??
?8?
7?
?8?
??
???
??
8?
??
??7
??
?
?8?
8?
8?
?7
7
9?
??
??
???
??9
??
9
9?
?9?
Решение:
Имеем выборку объемом n = ?? из генеральной совокупности Х,
представляющей собой еженедельный объем грузов.
Среди элементов выборки определим минимальное и максимальное
значения: xmin = ?, xmax = ?8?. Уменьшим xmin и xmax до «хороших» чисел, и
возьмем несколько больший промежуток от ? до ?88.
11
(...В представленной на сайте версии работы изменены числовые данные. Для получения
работы с корректными величинами, обратитесь на www.diplomant-spb.ru ...)
Вычислим размах выборки R = ?88 – ? = ?88.
Количество групп определим по формуле k = ? * Lg n = ? * Lg?? = 8.
Длину интервала найдем по формуле: h = R / k = ?88 / 8 = 8?.
Расчет параметров проведем с помощью MS Excel.
Рис. ? – Вид листа в табличном виде.
Переведем лист в режим проверки формул:
A
?
?
?
?
?
?
7
8
9
C
D
E
F
G
H
Статистические данные
??
??
??
??
?8?
98
??
??
??
?8
??
??
??
??8
??
??7
87
?7?
??
?8?
?8
B
?7?
??
???
??
???
??
?8?
7?
?8?
??
???
??
8?
??
??7
??
?
?8?
8?
8?
?7
7
9?
??
??
???
??9
??
9
9?
?9?
12
(...В представленной на сайте версии работы изменены числовые данные. Для получения
работы с корректными величинами, обратитесь на www.diplomant-spb.ru ...)
??
Макс
=МАКС(
A?:H8)
?88
Мин
=МИН(A?:
H8)
?
Группа
?
Лев.гран
=C??
??
?
?7
??
??
n
R
k
h
??
??
??
??
=B??-C??
8
=B??/E??
Прав.гран.
=F??
Середина
=B??+(C??B??)/?
Отн.част.
=E??/$A$??
Нак.част.
=E??
Н.о.част
=G??/$A$??
=C??
=B??+$F$??
=B??+(C??B??)/?
=E??/$A$??
=G??+E??
=G??/$A$??
?
=C??
=B?7+$F$??
=B?7+(C?7B?7)/?
=E?7/$A$??
=G??+E?7
=G?7/$A$??
?8
?
=C?7
=B?8+$F$??
=B?8+(C?8B?8)/?
=E?8/$A$??
=G?7+E?8
=G?8/$A$??
?9
?
=C?8
=B?9+$F$??
=B?9+(C?9B?9)/?
=E?9/$A$??
=G?8+E?9
=G?9/$A$??
??
?
=C?9
=B??+$F$??
=B??+(C??B??)/?
=E??/$A$??
=G?9+E??
=G??/$A$??
??
7
=C??
=B??+$F$??
=B??+(C??B??)/?
=E??/$A$??
=G??+E??
=G??/$A$??
??
8
=C??
=B??+$F$??
=B??+(C??B??)/?
Частота
=ЧАСТОТ
А(A?:H8;C?
?:C??)
=ЧАСТОТ
А(A?:H8;C?
?:C??)
=ЧАСТОТ
А(A?:H8;C?
?:C??)
=ЧАСТОТ
А(A?:H8;C?
?:C??)
=ЧАСТОТ
А(A?:H8;C?
?:C??)
=ЧАСТОТ
А(A?:H8;C?
?:C??)
=ЧАСТОТ
А(A?:H8;C?
?:C??)
=ЧАСТОТ
А(A?:H8;C?
?:C??)
=СУММ(E?
?:E??)
=E??/$A$??
=G??+E??
=G??/$A$??
??
??
??
??
Средне
е
=СРЗН
АЧ(A?:
H8)
Дисп.
=ДИСП(
A?:H8)
=СУММ(F?
?:F??)
Ср.кв.откл
.
=КОРЕНЬ(
B??)
На основе полученных данных построим графики:
13
(...В представленной на сайте версии работы изменены числовые данные. Для получения
работы с корректными величинами, обратитесь на www.diplomant-spb.ru ...)
Полигон частот
Частоты
35
30
25
20
15
10
5
0
43
129
215
301
387
473
559
645
Середины интервалов
Накопленные частоты
Кумулятата частот
60
50
40
30
20
10
0
43
129
215
301
387
473
559
645
Середины интервалов
14
(...В представленной на сайте версии работы изменены числовые данные. Для получения
работы с корректными величинами, обратитесь на www.diplomant-spb.ru ...)
Гистограмма выборки
35
y
30
25
20
15
10
5
0
43
129
215
301
387
473
559
645
х
?. СЕТЕВОЕ ПЛАНИРОВАНИЕ.
Построить сетевую модель и произвести расчет ее временных
параметров методом сетевого планирования на основе заданной структуры.
Работа
Опирается на работы
Длит.
а?
-
-
-
7
а?
-
-
-
?
а?
-
-
-
?
а?
-
-
-
?
а?
а?
-
-
?
а?
а?
-
-
?
15
(...В представленной на сайте версии работы изменены числовые данные. Для получения
работы с корректными величинами, обратитесь на www.diplomant-spb.ru ...)
а7
а?
а?
-
?
а8
а?
а?
-
?
а9
а?
а?
-
7
а??
а?
а7
-
?
а??
а?
а?
а8
?
а??
а?
а?
а8
?
а??
а?
а?
а8
7
а??
а9
а??
-
?
а??
а??
-
-
?
а??
а??
а??
а??
7
Решение:
Для работы с сетевым графиком необходимо провести упорядоченную
нумерацию событий. События являются упорядоченными, если для каждой
работы номер ее начального события меньше номера ее конечного события.
3
5
7
0
6
2
1
8
4
16
(...В представленной на сайте версии работы изменены числовые данные. Для получения
работы с корректными величинами, обратитесь на www.diplomant-spb.ru ...)
?. ВЫПУСК ПРОДУКЦИИ ПРИ НЕОПРЕДЕЛЕННОМ СПРОСЕ.
В результате производства и реализации единицы продукции А?, А?, А?
завод получает чистый доход, зависящий от спроса на продукцию, который
может принимать одно из состояний В?, В?, В?, В? (заранее неизвестно, какое
именно). Возможные значения дохода представлены платежной матрицей. В
17
(...В представленной на сайте версии работы изменены числовые данные. Для получения
работы с корректными величинами, обратитесь на www.diplomant-spb.ru ...)
каких пропорциях следует выпускать продукцию А?, А?, А?, чтобы
гарантировать максимальный чистый доход при любом состоянии спроса.
Для этого необходимо:
 Представить задачу о выпуске продукции как матричную игру
предприятия с «природой», считая спрос на продукцию полностью
неопределенным;
 Произвести упрощение платежной матрицы, используя принцип
доминирования;
 Найти оптимальные стратегии игроков и цену игры;
 Определить оптимальные пропорции в выпускаемой продукции с
целью получения максимальной выгоды предприятию;
 Определить наиболее выгодный для завода вид продукции, используя
критерии Лапласа, Вальда и Сэвиджа.
Платежная матрица имеет вид:
Вид
Доход в зависимости от спроса на продукцию
продукции
B?
B?
B?
B?
A?
?
8
?
8
A?
8
9
8
?
A?
?
?
?
?
Решение:
Рассмотрим поставленную задачу как матричную игру двух лиц: игрок
А – завод (три чистых стратегии) и игрок В – «природа» (четыре чистых
стратегии)
Проведем расчеты в Excel:
18
(...В представленной на сайте версии работы изменены числовые данные. Для получения
работы с корректными величинами, обратитесь на www.diplomant-spb.ru ...)
Подготовим лист для расчетов:
 Ячейки В?:Е? – элементы платежной матрицы
 Ячейки G?:G? – вероятности применения чистых стратегий игроком А
 Ячейки В?:Е? - вероятности применения чистых стратегий игроком В
Для расчетов воспользуемся надстройкой «Поиск решения»
19
(...В представленной на сайте версии работы изменены числовые данные. Для получения
работы с корректными величинами, обратитесь на www.diplomant-spb.ru ...)
Продолжим вычисление (кнопка «Выполнить») и получим следующие
значения:
Обратимся к процедуре «Поиск решения»:
Продолжим вычисление (кнопка «Выполнить») и получим следующие
значения:
20
(...В представленной на сайте версии работы изменены числовые данные. Для получения
работы с корректными величинами, обратитесь на www.diplomant-spb.ru ...)
Из полученных результатов находим:
 В ячейках G?:G? оптимальную стратегию игрока А, Р*=(?.??????,
?.??????, ?.??????);
 В ячейках В?:Е? оптимальную стратегию игрока В, Q* = (?, ?, ?, ?);
 В ячейках I? и F8 цену игры vmin = ?.??? и vmax = 9.
21
(...В представленной на сайте версии работы изменены числовые данные. Для получения
работы с корректными величинами, обратитесь на www.diplomant-spb.ru ...)
?. ЗАДАЧА О КОНКУРИРУЮЩИХ СУПЕРМАРКЕТАХ.
Три супермаркета конкурируют между собой с целью привлечения
возможно большего количества покупателей. На ? января известно
распределению покупателей по супермаркетам в процентах. Фирма по
изучению рынка подметила за прошлый год некоторые закономерности в
средних ежемесячных переходах покупателей из одного супермаркета в
другой. Требуется сделать прогноз о возможном количестве покупателей в
каждом
супермаркете,
предполагая
общее
количество
покупателей
постоянным.
Решить задачу при следующих данных. На ? января магазин А
посещало ??%, магазин В – ??%, магазин С – ??% всех покупателей.
За предыдущий год в среднем за месяц:
Магазин А сохранил 87% своих покупателей и получил 8%
покупателей магазина В и ?% покупателей магазина С.
Магазин В сохранил ??% своих покупателей и получил ??%
покупателей магазина А и ??% покупателей магазина С.
Магазин С сохранил 88% своих покупателей и получил 7%
покупателей магазина А и ?% покупателей магазина В.
Решение:
Рассмотри переход покупателей как цепь Маркова.
?.??
S2
0.21
0.15
0.08
0.87
0.05
S1
S3
0.88
0.07
0.05
22
(...В представленной на сайте версии работы изменены числовые данные. Для получения
работы с корректными величинами, обратитесь на www.diplomant-spb.ru ...)
Матрица переходных вероятностей имеет вид:
.870
.080
.05
0



P

.210
.640
.15
0

0

.050
.88
 .070

По условию вектор начальных вероятностей равен π? = (?.?; ?.?; ?.?).
Поэтому прогноз на ? февраля равен:
π = π * Р = (?.?; ?.?; ?.?) *
(?)
?
.87 0
.08 0
.05
0



.21 0
.64 0
.15
0
=
0

.05 0
.88
 .07 0

(?.?9?; ?.???; ?.???)
Прогноз распределения покупателей на ? марта:
π(?) = π? * Р = (?.?9?; ?.???; ?.???) *
.87 0
.08 0
.05
0



0
.
21
0
.
64
0
.
15

=(?.?78;
0

.
07
0
.
05
0
.
88


?.???; ?.??)
Для оценки состояния рынка в установившемся режиме необходимо
решить систему уравнений π = π * Р. В матричном виде эта система
уравнений имеет вид:
(π?; π?; π?) *
.87 0
.08 0
.05
0



0
.
21
0
.
64
0
.
15

=(π?;
0

.
07
0
.
05
0
.
88


0
.
87

1

0
.
21

2

0
.
07

3


1


0
.
08

1

0
.
64

2

0
.
05

3


2


0
.
05

1

0
.
15

2

0
.
88

3


3

=>
π?; π?), откуда

0
.
13

1

0
.
21

2

0
.
07

3


1


0
.
08

1

0
.
36

2

0
.
05

3


2


0
.
05

1

0
.
15

2

0
.
12

3


3

Дальнейший расчет проведем с помощью MS Excel:
23
(...В представленной на сайте версии работы изменены числовые данные. Для получения
работы с корректными величинами, обратитесь на www.diplomant-spb.ru ...)
В режиме проверки формул лист будет выглядеть следующим образом:
Воспользуемся надстройкой «Поиск решения»:
24
(...В представленной на сайте версии работы изменены числовые данные. Для получения
работы с корректными величинами, обратитесь на www.diplomant-spb.ru ...)
Продолжим вычисление и получим следующий результат:
Таким образом, получено решение системы уравнений
π = (?.??89; ?.???; ?.?8??)
25
(...В представленной на сайте версии работы изменены числовые данные. Для получения
работы с корректными величинами, обратитесь на www.diplomant-spb.ru ...)
Это значит что при длительной работе магазин А будут посещать
??.89% покупателей, магазин В – ??.?% покупателей, магазин С – ?8.??%
покупателей).
Дата
Посещаемость супермаркетов
А
В
С
? января
??
??
??
? февраля
?9.?
??.?
??.?
? марта
?7.8
??.?
??
??.89
??.?
?8.??
………..
Длительный срок
Из таблицы видно, что происходит снижение активности в магазинах
А и В, и увеличение покупательской активности в магазине С с ??% до
?8.??%.
26