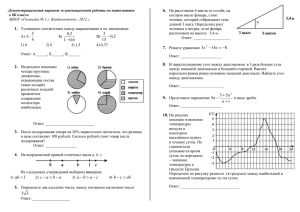
Четырехугольники І. Произвольный четырехугольник АВСD.
реклама
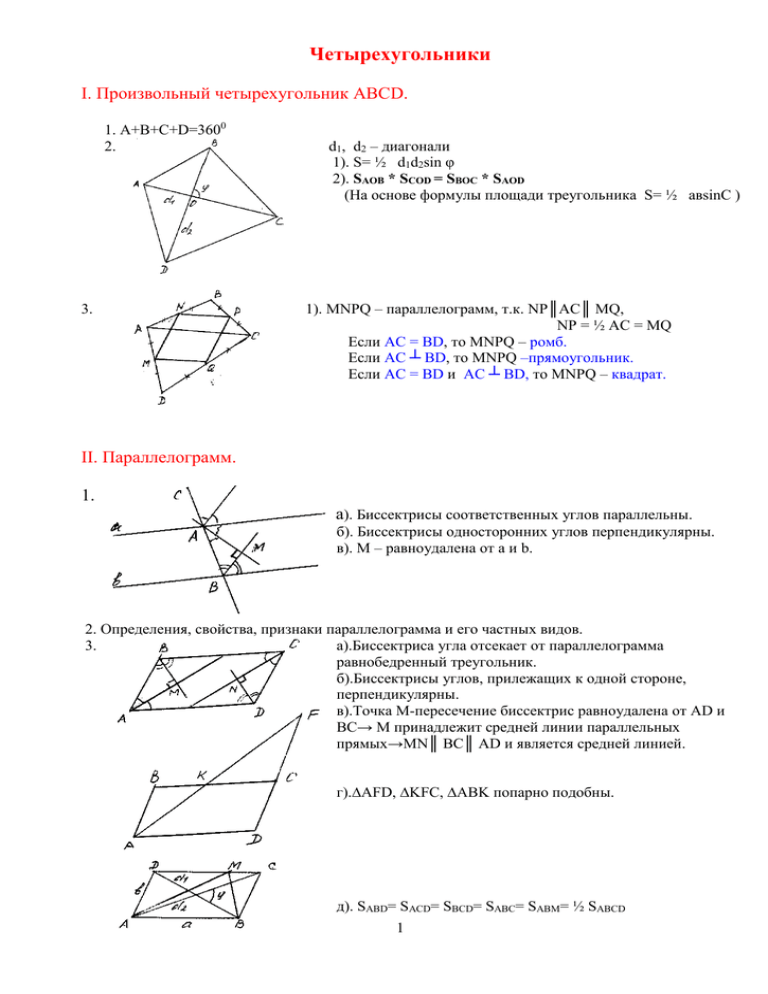
Четырехугольники І. Произвольный четырехугольник АВСD. 1. А+В+С+D=3600 2. 3. d1, d2 – диагонали 1). S= ½ d1d2sin φ 2). SАОВ * SСОD = SВОС * SАОD (На основе формулы площади треугольника S= ½ авsinС ) 1). МNPQ – параллелограмм, т.к. NP║AC║ MQ, NP = ½ AC = MQ Если AC = BD, то MNPQ – ромб. Если AC ┴ BD, то MNPQ –прямоугольник. Если AC = BD и AC ┴ BD, то MNPQ – квадрат. ІІ. Параллелограмм. 1. а). Биссектрисы соответственных углов параллельны. б). Биссектрисы односторонних углов перпендикулярны. в). М – равноудалена от а и b. 2. Определения, свойства, признаки параллелограмма и его частных видов. 3. а).Биссектриса угла отсекает от параллелограмма равнобедренный треугольник. б).Биссектрисы углов, прилежащих к одной стороне, перпендикулярны. в).Точка М-пересечение биссектрис равноудалена от АD и ВС→ М принадлежит средней линии параллельных прямых→MN║ BC║ AD и является средней линией. г).∆AFD, ∆KFC, ∆ABK попарно подобны. д). SABD= SACD= SBCD= SABC= SABM= ½ SABCD 1 е).d12 +d22 =2(а2 +в2) ж). S= ahа= bhb = absinA = ½ d1d2sinφ ІІІ.Трапеция. 1. а).∆АВF- равнобедренный б).<AMB = 900, <CND = 900 в). М, N равноудалены от прямых ВС и АD→ МN лежит на средней линии трапеции. а). SABD = SACD , SABC = SDBC , SAOB = SCOD 2. б). S2AOB = SBOC* SAOD. в).SAOD ∕SCOB = а2/в2 =АО2/ОС2 ; SAOB/SAOD = OB/OD; SBOC/SCOD = OB/OD =CO/OA = b/a г). S = ½(a+b)h = MN *h , т.к. MN – средняя линия MN= ½ (a+b) д). SAQB = ½ SABCD 3. Если AD= BC, то AC = BD, <DAB =<CBA, <D= <C. AH = MN (средняя линия), S = AH *CH. 4. Дополнительные построения. а).Высоты из вершин меньшего основания. б). в). CM║AD→CM = AD, BM = a-b CM║DB→ CM = DB, AM = a+b, SACM=SABCD г). MQ║AD , MP║CB → QP = a-b, <QMP = <(DA, CB) 2 Геометрия четырехугольника (подготовка к ЕГЭ-2011). 1.В прямоугольный треугольник с катетами 3 и 5 вписан квадрат, имеющий с треугольником общий прямой угол. Найдите периметр квадрата. 2. В параллелограмме ABCD AB = 4, AD = 8. Биссектрисы углов пересекаются в точке К, углов С и Д – в точке М. Найдите КМ. A и В 3. Биссектрисы углов A и D параллелограмма АВСD пересекают сторону BC в точках K и M соответственно, причем эти точки делят сторону BC на три равные части. AK =8, DM = 6. Найдите периметр параллелограмма. 4. На стороне AB параллелограмма ABCD отмечены точки K и M так, что AK = KM = MB. Отрезки CK и DM пересекаются в точке O. Площадь параллелограмма равна 40. Найдите площадь треугольника COD. 5. Дан ромб ABCD, его диагонали равны 6 и 8. Из вершины тупого угла В проведены высоты ВЕ и BF. Найдите площадь четырехугольника. 6. Найдите площадь параллелограмма, если длины его сторон равны a и b , а угол между диагоналями, противолежащий стороне длиной a, равен α. 7. Найдите площадь параллелограмма, если длины его диагоналей равны m и n , а угол параллелограмма, противолежащий диагонали n , равен φ. 8. В выпуклом четырехугольнике ABCD точки K, L, M и N являются серединами сторон AB, BC, CD, DA соответственно. O– точка пересечения отрезков KM и LN. Известно, что <LOM = 900 и KM = 3LN. Найдите длины диагоналей AC и BD , если площадь четырехугольника KLMN равна S . 9. Основания трапеции равны 6 и 10, а боковые стороны 2 и 4. Биссектрисы углов при одной боковой стороне пересекаются в точке А, а при другой – в точке В. Найдите АВ. 10. Сумма углов при одном основании трапеции равна 900, а основания равны a и b. Найдите расстояние между серединами оснований. 11. Дана трапеция ABCD с боковыми сторонами AB = 36, CD = 34 и верхним основанием BC = 10. Известно, что cos<ABC = ─1/3 . Найдите BD. 3 12. Диагонали равнобедренной трапеции перпендикулярны и точкой пересечения делятся в отношении 3:4. Площадь четырехугольника с вершинами в серединах сторон трапеции равна 196. Найдите боковую сторону трапеции. 13. Диагонали равнобедренной трапеции перпендикулярны, одно из оснований равно 17, а площадь равна 81. Найдите второе основание трапеции. 14. В трапеции ABCD основания равны 13 и 26, одна из боковых сторон равна 5, а <C ─ <A = 900. Найдите площадь трапеции. 15. Основание AD равнобедренной трапеции ABCD в 5 раз больше основания BC. Высота BH пересекает диагональ в точке M, площадь треугольника AMH равна 4. Найдите площадь трапеции. 16. В трапеции ABCD с длинами оснований AD = 12, BC = 8 на луче BC построена такая точка M, что прямая AM делит трапецию на две равновеликие фигуры. Найдите длину CM. 17. Сумма длин высоты и средней линии равнобедренной трапеции равна площадь трапеции равна S. Найдите угол между диагоналями трапеции. c, а 18. В трапеции ABCD основания AD и BC равны a и b соответственно. Через точку Е, принадлежащую стороне AB и делящую ее в отношении AE: BE = m : n, проведена прямая, параллельная основаниям трапеции и пересекающая сторону CD в точке F. Докажите, что EF =( an +bm)/ (m+n). (Или : Найдите EF). 19. На боковых сторонах AB и CD трапеции ABCD с основаниями AD и BC отмечены точки P и Q соответственно, причем PQ ║AD. Прямая PQ разбивает трапецию на две трапеции, площади которых относятся как 1: 2 . Найдите PQ ,если AD = a и BC = b. 20. В трапеции основания равны 28 и 14, а боковые стороны 13 и 15. Через точку пересечения диагоналей параллельно основаниям проведена прямая. Найдите площадь получившихся трапеций. 21. В трапеции диагонали равны 3 и 5, а отрезок, соединяющий середины оснований, равен 2. Найдите площадь трапеции. 4