Задания .
реклама
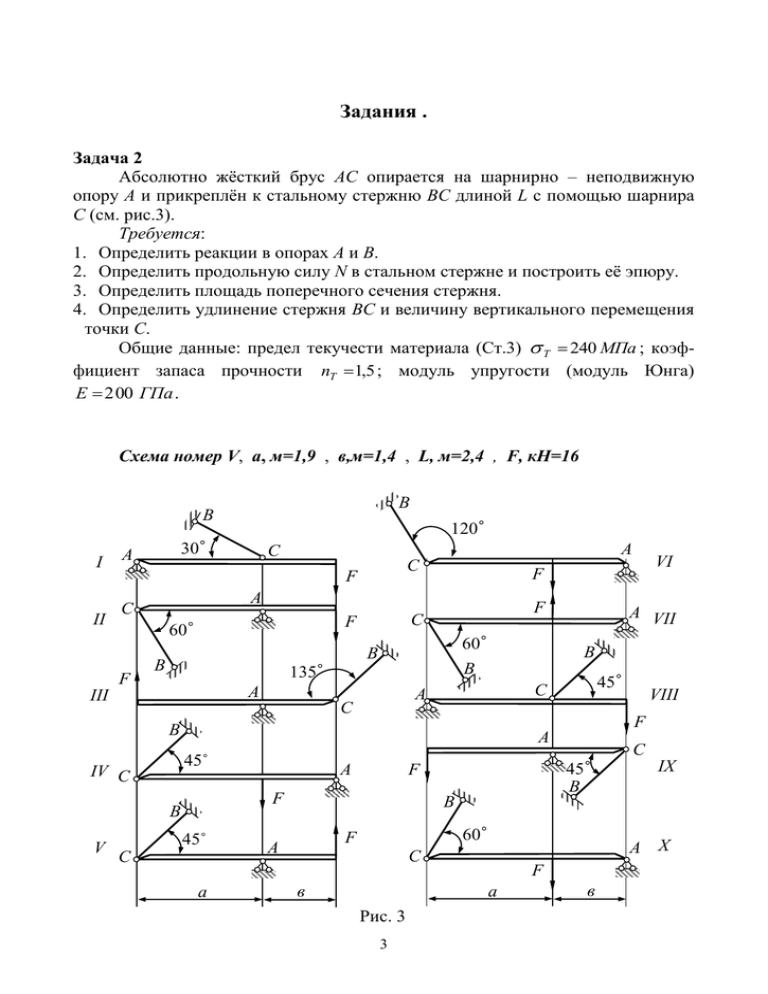
Задания . Задача 2 Абсолютно жёсткий брус АС опирается на шарнирно – неподвижную опору А и прикреплён к стальному стержню ВС длиной L с помощью шарнира С (см. рис.3). Требуется: 1. Определить реакции в опорах А и В. 2. Определить продольную силу N в стальном стержне и построить её эпюру. 3. Определить площадь поперечного сечения стержня. 4. Определить удлинение стержня ВС и величину вертикального перемещения точки С. Общие данные: предел текучести материала (Ст.3) Т 240 МПа ; коэффициент запаса прочности nT 1,5 ; модуль упругости (модуль Юнга) E 2 00 ГПа . Схема номер V, а, м=1,9 , в,м=1,4 , L, м=2,4 , F, кН=16 B I II 30˚ А B 120˚ А C C F 60˚ B B 60˚ B 135˚ B B IV C А FB B 45˚ C а 45˚ B F B F а Рис. 3 3 IX B А X C в C B 60˚ F А VIII F А 45˚ B 45˚ B C А C А VII B BB А III F C F VI F А C F V B B в Задача 3 К стальному валу приложены три вращающих момента (рис.4). Требуется: 1. Определить реактивный момент в заделке. 2. Построить эпюру крутящих моментов. 3. Определить диаметр вала (расчёты произвести из условия прочности и условия жёсткости). 4. Построить эпюру углов закручивания. Общие данные: допускаемое касательное напряжение 50 МПа ; допускаемый относительный угол закручивания 0 ,5 o м 1 ; модуль сдвига G 80 ГПа . Схема номер V а, м=1,9 в, м=1,4 с, м=0,5 М1, кН·м=9 , М2, кН·м=5 М3, кН·м=4 М3 М2 М1 М1 I М2 М3 VI М3 М2 М1 М1 М2 М3 М3 М2 М1 М1 М2 М3 М1 М2 М3 М1 М2 М3 II III VIII М3 М2 М1 IV IX М2 М3 М1 V X а в с а Рис. 4 4 в Таблица 4 с Задача 4 Даны две схемы стальных балок (рис.5). Требуется: Для схемы «б»: 1. Построить эпюры поперечной силы Q и изгибающего момента M. 2. Подобрать сечения следующей формы: прямоугольное (h[b = k); круглое; кольцевое (α = d[D); состоящее из двух швеллеров; двутавровое. 3. Оценить эффективность формы сечения. Общие данные: предел текучести материала Т 240 МПа ; коэффициент запаса прочности nT 1,5 ; модуль упругости (модуль Юнга) E 200 ГПа . Схема "б" номер V а1, м=1,0 М, кН·м=25 а2, м=1,4 q, кН/м=18 F, кН=25 α=0,8 k=2,5 M q q F I F q M q II q M q III F M F q q IV q M q V F a1 a1 a2 a2 б) a) Рис. 5 5 Задача 8 Стальной стержень длиной l сжимается силой F (рис.9). Требуется: 1. Найти размеры поперечного сечения стержня при допускаемом напряжении на центральное сжатие 160 МПа , пользуясь методом последовательных приближений. 2. Найти величину критической силы, если предельная гибкость пред 100 . 3. Найти коэффициент запаса устойчивости. Схема номер I Форма сечения I F, кН=400 6 l, м=2,5 F a a II a I a I l 0.2a 1.5a a IV a III F 1.5a II 0.2a l 2d V a d VI F 2d a a III l VII VIII d d 0.2d F IV X a IX 2a a l 2a 0.2a Рис. 9 7 Примеры решения задач Задача 2 (рис.12) Постановку задачи см. в практической части задания к курсовой работе (задача 2). Исходные данные: Предел текучести материала стержня (Ст. 3) T 240 МПа ; коэффициент запаса прочности nT 1,5 ; модуль Юнга E 200 ГПа ; a = 1м; b = 2м; L = 2м; F = 20 кН. Решение: I. Определяем реакции в опорах D и В. Рассматриваемая система является статически определимой, поскольку число связей, накладываемых на систему, соответствует числу уравнений равновесия статики в плоскости. Последних всегда три. В нашем случае в опоре В возникает только одна реакция в направлении продольной оси стержня ВС (реакция R В ), в опоре D – две ( R D и H D ), так как она является шарнирно неподвижной опорой (см. рис. 12, а). Составляем уравнения равновесия статики. Желательно каждое уравнение представить так, чтобы оно содержало только одну неизвестную. F a b 20 1 2 M D 0; F a b RB a sin 0 RB a sin 60 1 0,866 69,3 кН . Y 0; RB sin RD F 0 X 0; RB cos H D 0 RD RB sin 60 F 69 ,3 0,866 20 40 кН . H D RB cos 69 ,3 0,5 34 ,65 кН . Проверка правильности определения реакций: M C F b RD a 0, 20 2 40 1 0, 0 0 . Проверка обязательна. Полученное тождество свидетельствует о правильности результатов. II. Определяем продольную силу N в стальном стержне и строим её эпюру. Пользуясь методом сечения, определяем значение продольной силы N в сечении m – n стержня ВС (см. рис. 12, б): N RB 69 ,3 кН . Строим эпюру продольной силы. Поскольку при изменении значения координаты сечения m – n в пределах длины стержня продольная сила остаётся постоянной, эпюра продольной силы представляет собой прямую, параллельную оси абсцисс (см. рис. 12, б). C RB ΔL Y C2 Δверт α RB B B n L m 8 X C1 RD N III. Определяем площадь поперечного сечения стержня ВС. Условие прочности при растяжении для пластичных материалов: max , где max N max A ; max - наибольшее по абсолютной величине расчётное растягивающее напряжение, возникающее в сечении с продольной силой Nmax и с площадью поперечного сечения А. 240 Допускаемое напряжение T 160 МПа . nT 1,5 Из условия прочности решаем проектировочную задачу, математическая A N max . формулировка которой: Предельное значение площади 69 ,3 103 A 4,33 10 4 м 2 4,33 см 2 . 6 160 10 IV. Определяем удлинение стержня ВС и величину вертикального перемещения точки С. Удлинение стержня ВС определяем согласно закону Гука для абсолютных удлинений на основании следующей формулы: NL 69 ,3 103 2 L 1,6 10 3 м 1,6 мм . 11 4 E A 2 10 4,33 10 Вертикальное перемещение точки С находим, заменяя дугу (радиусом L L ) перпендикуляром С2С1 на первоначальное направление стержня (см. рис. 12, а). Малая величина удлинения L 1,6 10 3 м по сравнению с длиной стержня L 2 м допускает такую замену при весьма незначительной погрешности результата. Из треугольника СС1С2 находим, что вертикальное перемещение L 1,6 10 3 Δверт СС1 1,85 10 3 м 1,85 мм . sin 0,866 9 Задача 3 Постановку задачи см. в практической части задания к курсовой работе (задача 3). Решение типовой задачи см. в [1] пример 6.1; c. 195-199. Задача 4 Схема «а» (рис.13) Постановку задачи см. в практической части задания к курсовой работе (задача 4, схема «а»). Исходные данные: F 15 кН , q 10 кН м , а1 2 м , а2 1 м , T 240 МПа , nT 1,5 . Решение: I. Построим эпюры поперечной силы Q и изгибающего момента M. Получим выражения для Q и M по участкам. Заданная балка имеет два участка нагружения: по длине первого участка распределена равномерная нагрузка q, прекращение действия которой означает начало второго участка (см. рис. 13, а). На рисунке z1 и z 2 - координаты поперечных сечений первого и второго участков. Для каждого участка выбирается своя система координат. 0 z1 a1 . I – ый участок: Рассматривая равновесие левой отсечённой части балки (см. рис. 13, б), запишем выражения для Q z1 и M z1 : Q z1 F q z1 . Полученное выражение представляет собой уравнение наклонной прямой, следовательно, для её построения необходимо определить координаты двух точек. Мы выберем крайние точки: z1 0, Q z1 F 15 кН ; z1 a1 2 м , Q z1 F q a1 15 10 2 5 . z M z1 F z1 q z1 1 . 2 Равнодействующая распределённой нагрузки q на участке z1 равняется q z1 и приложена в середине участка, то есть расстояние от силы q z1 до сечения равно z1 2 . Данное выражение изгибающего момента представляет собой уравнение кривой второго порядка, имеющей экстремум в сечении с координатой z 0 , в котором Q z0 0 (см. ответ на вопрос 3 раздела 6). Следовательно, для построения эпюры M требуются координаты трёх точек: q a12 10 2 2 z1 0, M z1 0 ; z1 a1 2 м M z1 F a1 15 2 10 кН м . 2 2 F 15 При z1 z0 Q z0 F q z0 0 z0 1,5 м . q 10 q z02 10 1,52 Тогда M z0 F z0 15 1.5 11,25 кН м . 2 2 10 II – ой участок: 0 z 2 a2 . Рассматривая равновесие левой части, отсечённой сечением с координатой z 2 (см. рис. 13, в), запишем выражения для Q z 2 и M z 2 : Q z 2 F q a1 15 10 2 5 кН const . Полученное выражение представляет собой уравнение прямой, параллельной оси эпюры. M z2 F a1 z2 q a1 0,5 a1 z2 . q q а) M(z1) z1 F F z1 Q(z1) z2 a2 a1 б) M(z2) q 15 0 + + 0 10 q Y 11.25 Q(z2) в) 0 z0 Э M, кН·м z2 a1 F Э Q, кН 5 Z 5 0 F z1 z2 г) Рис. 13 В данном случае мы получили уравнение прямой, наклонной к оси эпюры. Для её построения определим координаты двух крайних точек: z2 0, M z2 F a1 0,5 q a12 15 2 0,5 10 22 10 кН м ; z2 a2 1 м; M z2 F a1 a2 q a10,5a1 a2 152 1 10 20,5 2 1 5 кН м. Строим эпюры Q и M. Результат представлен на рис. 13, а. II. Определяем максимальное нормальное напряжение в балке сложного поперечного сечения, уже рассмотренного в задаче 1. Для этого следует воспользоваться формулой M max 11.25 103 max 0,06368 109 Па 63,68 МПа . 6 Wx 176 ,66 10 III. Определяем фактический коэффициент запаса прочности как 240 nT* T 3,77 . max 63,68 11 Конструкция пригодна к эксплуатации, так как действительный запас прочности больше нормативного nT* nT , то есть 3,77 > 1,5. IV. Определяем прогиб конца консоли аналитическим методом. Составляем приближённые дифференциальные уравнения изогнутой оси балки по участкам с соблюдением условий Клебша (см. ответ на вопрос 11 раздела 6). Необходимо отметить, что в этом случае выбирается только одна система координат с началом в крайней левой точке балки (см. рис. 13, г). Если в этой точке балка жёстко или шарнирно зафиксирована, то прежде чем приступить к составлению уравнений, необходимо определить реакции в опорах. Для нашего случая: q z12 0 z a I – ый участок: ; EI X y z1 F z1 1 1, 2 q z 22 q z 2 a1 2 II – ой участок: a1 z 2 a1 a2 , EI X y z 2 F z 2 . 2 2 Дважды интегрируем дифференциальные уравнения EI y z1 F z12 2 q z13 6 C1 1 I - ый участок X 3 4 2 EI X y z1 F z1 6 q z1 24 C1z1 D1 . EI X y z2 F z22 2 q z23 6 q z2 a1 3 6 C2 3 II - ой участок 4 3 4 EI X y z2 F z2 6 q z2 24 q z2 a1 24 C2 z2 D2 . 4 Рассматриваем граничные условия и доказываем равенство постоянных интегрирования на обоих участках. При z1 z 2 a1 (на границе двух смежных участков балки) y1 y 2 , y1 y 2 , так как они являются углами поворота и прогибами, соответственно, одного и того же сечения. Тогда, учитывая формулы (1) и (3), получим: 3 2 Fa1 qa13 Fa12 qa13 qa1 a1 C1 C2 , откуда C1 C2 C . 2 6 2 6 6 Из формул (2) и (4) получим 4 Fa13 qa14 Fa3 qa4 qa1 a1 Ca1 D1 1 1 Ca1 D2 , откуда D1 D2 D . 6 24 6 24 24 Следовательно, имеют место только две постоянных интегрирования: C, D. Из начальных условий определяем значения постоянных интегрирования C и D. Первое условие: при z 2 a1 a2 3 м y z 2 0 , то есть в защемленном конце балки угол поворота равен нулю, иными словами сечение не поворачивается. Тогда согласно формуле (3) EI X y z 2 3 15 32 2 10 33 6 10 3 23 6 C 0 . Откуда C 24,2 кН м2 . 12 Второе условие: при z 2 a1 a2 3 м , y z 2 0 , то есть в защемленном конце балки прогиб равен нулю – сечение не перемещается вертикально. Тогда в соответствии с формулой (4) EI X y z 2 3 15 33 6 10 34 24 10 3 24 24 C 3 D 0 . Откуда D 33,4 кН м3 . Вычисляем прогиб конца консоли Для этого воспользуемся формулой (2) при z1 0 : y z1 D EI X 38,4 103 8 8 10 3 м 8 мм . 2 10 2395 ,52 10 Согласно принятому направлению координатных осей (см. рис. 13, г) при решении задачи аналитическим методом знак «+» указывает на то, что прогиб конца консоли балки направлен вверх. 11 Задача 4 Схема «б» (рис.14) Постановку задачи см. в практической части задания к курсовой работе (задача 4, схема «б»). Исходные данные: M 20 кН м , q 16 кН м , а1 1 м , а2 2 м , T 240 МПа , nT 1,5 . Решение: I. Построим эпюры поперечной силы Q и изгибающего момента M. Определяем опорные реакции балки. Заданная балка зафиксирована в двух сечениях с помощью шарнирно-подвижной и шарнирно-неподвижной опор (см. рис. 14). Характер прикладываемой нагрузки обуславливает необходимость определения только вертикальных реакций опор R A и RB , так как горизонтальная составляющая реакции в опоре А равна нулю ( H A 0 ). a2 0,5 qa22 M 0,5 16 22 20 26 кН . M A 0, RB a2 qa2 2 M 0 RB a2 2 a2 0,5 qa22 M 0,5 16 22 20 6 кН . M В 0, RAa2 M qa2 2 0 RA a2 2 Проверка: Y 0, R A RB qa2 ; 6 26 32 0; 0 0 . Полученное тождество свидетельствует о правильности результатов. Записываем уравнения для Q и M по участкам. Для каждого участка выбирается своя система координат 0 z1 a1 . I – ый участок: Рассматриваем равновесие левой части балки: Q z1 0, M z1 M 20 кН м const . 0 z 2 a2 . II – ой участок: Рассматриваем равновесие правой части балки: Q z 2 RB qz 2 . 13 z 2 0, Q z 2 RB 26 кН ; z 2 a 2 , Q z 2 RB qa 2 26 32 6 кН . M z 2 RB z 2 0.5 qz22 . z 2 0, M z 2 0; z 2 a2 2 м , M z 2 RB a2 0,5 qa22 26 2 0,5 16 2 2 20 кН м. R 26 При z 2 z0 Q z0 RB qz0 0 z0 B 1,625 м , q 16 qz02 16 1,625 2 тогда M z0 RB z0 26 1,625 21,125 кН м . 2 2 q Строим эпюры Q и M. РеRB RA M зультат представлен на рис. 14. A II. B Подбираем сечения указанных в задании форм. z1 z2 Условие прочности при изгибе по a2 a1 нормальным напряжениям для плаЭ Q, z0 стичных материалов: 6 кН 0 M max max , WX T 240 160 МПа . 26 где nT 1,5 21,125 20 Тогда условие проектировочной задачи принимает следующий вид: + Э M, M кН·м WX max . h Рис. 14 Так как M max 21,125 кН м (см. рис.14), то предельное значение осевого момента сопротивления: 21,125 103 WX 0,132 10 3 м3 . 6 160 10 Подбираем прямоугольное сечение. Соотношение сторон h b 2 (рис.15). y Так как для прямоугольного сечения момент сопротивления относительно оси X ( см. рис. 15) W X bh 2 6 и x по условию b h 2 , то: h 3 12WX 3 12 0,132 103 0,1166 м 11,66 см , b h 2 11,66 2 5,83 см , b Рис. 15 y d x Aпр h b 0,1166 0,0583 67 ,98 104 м2 . Подбираем круглое сечение. Для круглого сечения осевой момент сопротивления (рис. 16) W X D 3 32 ; тогда 14 Рис. 16 D 3 32WX 3 32 0,132 103 0,1104 м 11см ; Aкр D2 4 0,1104 2 4 0,0096 м2 . Подбираем кольцевое сечение. Отношение диаметров d D 0,8 (рис. 17). Для кольцевого сечения осевой момент сопротивления WX D3 32 1 4 . Тогда x d D y D 3 Рис.17 32WX 1 4 3 32 0,132 10 3 1 0,84 0,1316 м 13,16 см ; d D 0,8 0,1316 0,8 0,1053 м 10,53 см ; Aкц D2 1 2 4 0,1316 2 1 0,82 4 48,97 104 м2 . Подбираем сечение, состоящее из двух швеллеров. В основе определения осевого момента сопротивления лежит соотношение W X I X y max (см. решение задачи 1, пункт VI). Рассматриваемое сечение сложное (см. решение задаx чи 1, пункт V), состоит из двух равных частей (рис. 18): I Xшв1 I Xшв2 2 I Xшв I Xшв WX 2 2 W Xшв . y max y max y max Рис. 18 M M По условию проектировочной задачи W X 2W Xшв max W Xшв max . 2 Тогда предельное расчётное значение осевого момента сопротивления для одy ного швеллера WXшв 0,066 м3 66 см3 . По таблице ГОСТ 8240-72 выбираем швеллер № 14 с ближайшим большим моментом сопротивления ГОСТWXшв 70,2 см3 . Следовательно, площадь всего сече- A 2 ГОСТAшв 2 15,6 104 31,2 104 м2 31,2 см2 . y Подбираем двутавровое сечение. Условие проектировочной задачи для балки с двутавровым сеx чением (рис. 19): M ГОСТ WXдв max 0,132 10 3 м3 . По таблице ГОСТ 8239-72 выбираем двутавровую балку Рис.19 № 18 с ближайшим значением момента сопротивления, значение которого отвечает условию проектировочной задачи: ГОСТ WXдв 143 см3 ; ГОСТAдв 23,4 см2 . III. Оцениваем эффективность формы сечения. Для этого сравниваем площади всех подобранных сечений: ния балки 15 Aпр Aдв 67 ,98 2 ,91; 23,40 Aкр Aдв Aкц 96 ,00 4 ,10; 23,40 48 ,97 Aшв 31,20 2 ,09; 1,33. Aдв 23,40 Aдв 23,40 Наиболее эффективной формой сечения балки (балка с наименьшим весом) является двутавровое сечение, наименее эффективной – круглое сплошное сечение. 16 Задача 8 (рис. 21) Постановку задачи см. в практической части задания к курсовой работе (задача 8). Исходные данные: F 400 кН , L 3 м , E 200 ГПа , 1 (μ – коэффициент, зависящий от условий закрепления стержня, табличная величина). Решение: I. Находим размеры поперечного сечения стержня при допускаемом напряжении на центральное сжатие 160 МПа , пользуясь методом последовательных приближений. Записываем выражение для определения площади поперечного сечения стержня из условия устойчивости. F Условие устойчивости , A F F тогда , A (5) L А А d 2d A-A 3d где - коэффициент уменьшения допускаемого напряжения на сжатие, или коэффициент продольного изгиба. В расчётной формуле (5) имеются две неизвестные величины – коэффициент и искомая площадь A. Поэтому при подборе сечения необходимо использовать метод последовательных приближений. Для упрощения расчётов выполним вспомогательные преобразования. Так как проектируемое сечение сложное, минимальный момент инерции (потеря устойчивости происходит в плоскости наименьшей жёсткости) определяется следующим образом: b h3 d 4 3d 2d 3 d 4 I min 1,95 d 4 . 12 64 12 Рис. 21 Площадь поперечного сечения d2 A 2d 2d 5,21 d 2 . 4 d 0 ,44 A . Тогда Минимальный радиус инерции imin I min 1,95 d 4 0,61 d . A 5,21 d 2 imin 0,61 d . 17 64 (6) (7) Выполняем первое приближение. В первом приближении коэффициент продольного изгиба обычно принимают 1 0 ,5 , тогда A1 F 400 103 0,005 м 2 . 1 0,5 160 10 Используя соотношения (6) и (7), получим: d1 0,44 0,005 3,1102 м 3,1см ; 6 imin1 0,61 d1 0,61 3,1102 1,89 102 м . Тогда расчётная гибкость колонны: L 1 3 1 159 . imin1 1,89 10 2 По таблице ([1], табл. 13.1, с. 493) определяем значение коэффициента 1 , соответствующего гибкости 1 159 . 150 0,32; 160 0,29. Путём линейной интерполяции 0,32 0,29 1 0,32 9 0,293 . 10 Проверим выполнение условия устойчивости в первом приближении. Для этого вычислим рабочие напряжения первого приближения следующим образом: F 400 103 1 80000 103 Па 80 МПа . A1 0 ,005 Затем определим допускаемые напряжения по устойчивости в первом приближении как у 1 0,293 160 46,88 МПа . Из приведённых вычислений следует, что условие устойчивости не выполняется, так как 1 у 80 МПа 46,88 МПа . В этом случае перенапряжение составляет 1 у 80 46 ,88 1 100 % 100 % 70 ,65 % , у 46 ,88 что недопустимо. Следовательно, необходимо второе приближение. Выполняем второе приближение. Во втором приближении коэффициент продольного изгиба 0,5 0,293 2 1 1 0,396 . 2 2 Тогда площадь сечения F 400 103 2 A2 0 , 0063 м . 2 0,396 160 106 Диаметр d2 0,44 0,0063 3,5 102 м 3,5 см ; 18 радиус инерции imin 2 0,61 d2 0,61 3,5 102 2,135 10 2 м . Гибкость колонны 2 L 1 3 140 ,5 . 2,135 10 2 Определяем значение коэффициента 2 , соответствующего этой гибкости: 140 0,36; imin 2 150 0,32; 0,36 0,32 0,5 0,358 . 10 Проверим выполнение условия устойчивости во втором приближении. Для этого вычислим рабочие напряжения второго приближения F 400 103 2 63492 103 Па 63,492 МПа . A2 0,0063 Затем определим допускаемые напряжения по устойчивости во втором приближении у 2 0,358 160 57 ,28 МПа . Из приведённых вычислений следует, что условие устойчивости не выполняется, так как 2 у 63,492 МПа 57 ,28 МПа . В этом случае перенапряжение составляет 2 у 63,492 57 ,28 2 100 % 100 % 10 ,84 % , у 57 ,28 что опять недопустимо, так как перенапряжение превышает 5%. Следовательно, необходимо третье приближение. Выполняем третье приближение. В третьем приближении коэффициент продольного изгиба 0,396 0,358 3 3 3 0,377 . 2 2 Тогда площадь сечения F 400 103 2 . A3 0 , 0066 м 3 0,377 160 106 2 0,36 Диаметр d3 0,44 0,0066 3,6 102 м 3,6 см ; радиус инерции imin 3 0,61 d3 0,61 3,6 10 2 2,196 102 м . Гибкость колонны 3 L 1 3 136 ,6 . 2,196 10 2 Определяем значение коэффициента 3 , соответствующего этой гибкости. imin3 19 130 0,40; 140 0,36; 0,40 0,36 6,6 0,374 . 10 Проверим выполнение условия устойчивости в третьем приближении. Для этого вычислим рабочие напряжения третьего приближения F 400 103 3 60606 103 Па 60 ,606 МПа . A3 0,0066 Затем определим допускаемые напряжения по устойчивости в третьем приближении у 3 0,374 160 59,84 МПа ; 3 0,40 3 у 60 ,606 МПа 59,84 МПа . Из чего следует, что условие устойчивости не выполняется, однако перенапряжение составляет 3 у 60 ,606 59 ,84 3 100 % 100 % 1,28 % 5 % , у 59 ,84 что допустимо, так как оно не превышает 5%. То есть окончательно принимаем d 0,036 м 36 мм . Следовательно, сечение имеет размеры 72×108 см; I min 1,95 d 4 1,95 3,64 327 ,5 см4 ; 136,6 . II. Находим величину критической силы. Так как пред , то есть 136 ,6 100 , то используем формулу Эйлера для определения критической силы: 2 E I min 2 2 1011 327 ,5 10 8 3 Fкр 718 , 29 10 Н 718 ,29 кН . L 2 1 32 III. Определяем коэффициент запаса устойчивости следующим образом: Fкр 718 ,29 kу 1,8 . F 400 Задача 9 Постановку задачи см. в практической части задания к курсовой работе (задача 9). Решение типовой задачи см. в [1] пример 14.2; с. 537 – 540. Библиографический список 1. Дарков А.В., Шпиро Г.С. Сопротивление материалов. – М.: Высш. школа, 1989. – 624 с. 2. Писаренко Г.С. Сопротивление материалов. – Киев: Высш. школа, 1986. – 775 с. 3. Феодосьев В.И. Сопротивление материалов. – М.: Наука, 1986. – 512 с. 20 21