Чертежи

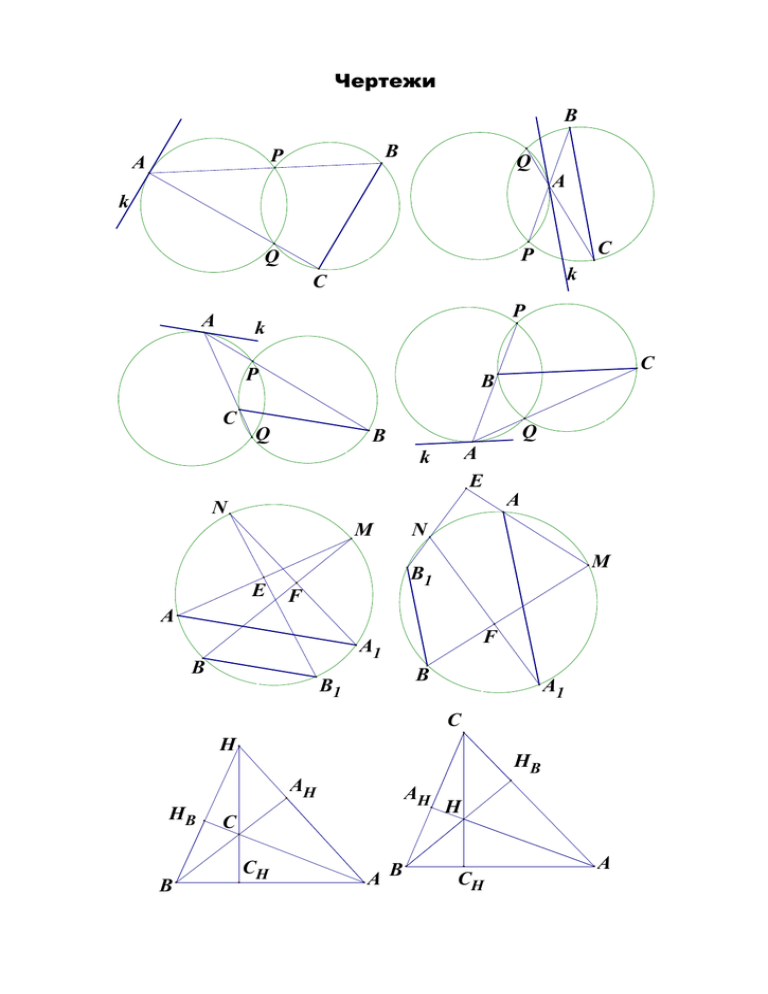
Чертежи
B
B
P
A
Q
A
k
C
P
Q
k
C
A
P
k
C
P
C
B
Q
Q
B
A
k
E
A
N
N
M
E
M
B1
F
A
F
A1
B
B
B1
A1
C
H
HB
AH
HB
B
AH
C
CH
A
B
H
CH
A
Направленные углы
1.
2.
3.
4.
5.
Величиной ориентированного угла между прямыми l1 и l2 (обозначение
(l1; l2)), будем называть величину угла, на который нужно повернуть против
часовой стрелки прямую l1 так, чтобы она стала параллельна прямой l2. При
этом, углы, отличающиеся на 180 n, где n – целое, считаются равными.
Свойства ориентированных углов:
1. l1 || l2 тогда и только тогда, когда (l1; l2) = 0o.
2. (l1; l2) + (l2; l1) = 0o;
3. (l1; l2) + (l2; l3) = (l1; l3);
4. Точки A, B, C и D лежат на одной прямой или принадлежат одной
окружности тогда и только тогда, когда (AB, BC) = (AD, DC).
Лемма. Для точек А и С ГМ точек Х, для которых (AХ, ХC) = α есть
окружность без точек А и С, либо точки А, Х, С лежат на одной прямой, если
α = 0.
Через M и K проведены прямые AB и СD соответственно, пересекающие
первую окружность в точках A и C, вторую – в точках B и D. Докажите, что
AC параллельна BD.
Две окружности пересекаются в точках Р и Q. Через точку А первой
окружности проведены прямые АР и АQ, пересекающие вторую окружность в
точках В и С. Докажите, что касательная в точке А к первой окружности
параллельна прямой ВС.
На окружности даны точки А, В, М и N. Из точки М проведены хорды МА1 и
МВ1, перпендикулярные прямым NB и NA соответственно. Докажите, что
АА1 ║ ВВ1.
Докажите, что высоты треугольника пересекаются в одной точке.
На плоскости дано восемь точек А1, А2, А3, А4, В1, В2, В3, В4. Оказалось, что
четвёрки точек (А1, А2, В1, В2), (А2, А3, В2, В3), (А3, А4, В3, В4), (А4, А1, В4, В1),
(А1, А2, А3, А4) лежат на одной окружности каждая. Докажите, что точки В1, В2,
В3, В4.лежат либо на одной прямой, либо на одной окружности.
Для самостоятельного решения
6. На плоскости дана четверка прямых общего положения. Вокруг каждого
треугольника, образованного любыми тремя из них описана окружность.
Докажите, что эти четыре окружности имеют общую точку (точка Микеля).
7. Окружности S1 и S2 пересекаются в точке А. Через точку А проведена прямая
пересекающая S1 в точке В, S2 в точке С. в точках С и В проведены
касательные к окружностям, пересекающиеся в точке D. Докажите, что угол
BDC не зависит от выбора прямой, проходящей через А.