Домашняя работа 2
реклама

Домашнее задание 2
Студента(-ки) Иванова Ивана Петровича, группа АБВ123
Инструкции по оформлению:
1. Пользуйтесь этим файлом, заменив имя вверху (и в названии файла) на Ваше.
2. В пунктах, где оставлены пустые поля, впишите Ваши решения и ответы. Размер поля
никак не соответствует ожидаемому размеру решения: пишите всё необходимое.
Все решения (кроме применения программы BF.m в последнем разделе) должны быть
сделаны «вручную», т.е без применения каких-либо программ.
3. Помимо данного файла, Вы должны будете сдать программу фильтра BF.m (см. последнее
задание). Упакуйте все файлы (выполненное задание в этом файле, и BF.m) в .zip (с Вашим
именем латиницей в названии), и отправьте мне.
4. Задачи со * - бонусные. Рекомендую интересующимся и всем, у кого были проблемы с
первой домашней работой, для дополнительных баллов.
1 Преобразование Радона (задача из лекции)
4
2
x1
x2
x3
x4
Рис. 2
4
2
3
x1
x2
3
3
x3
x4
3
3
Рис. 1
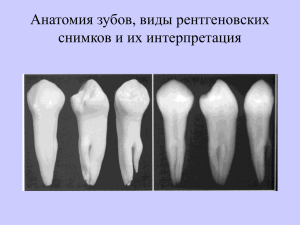
Рассмотрим задачу нахождения четырех неизвестных xi из их «рентген-проекций», определяемых
как суммы (например, x1+ x3=4).
A. Найдите значения xi на Рис. 2, используя x4 как независимую переменную:
B. Назовем решение задачи на Рис. 2 гладким, если значения xi минимально отклоняются от
своего среднего:
x
1
4
4
x
i
1
4
E
x x
2
i
min
1
Подобное условие гладкости может быть рассмотрено как полезное на практике условие
подавления нежелательных ошибок (шумов) в изображении.
Найдите xi в случае гладкого решения (напишите решение и ответ ниже):
C. Найдите решение в А. при добавлении еще одной «рентгеновской» проекции x2+ x3=3 (Рис.
1):
D. Что можно сказать о решениях в B. и C., какое из них будет более предпочтительным для
применения в клинике (и почему)?
2 Формула билатерального фильтра
Как было определено на лекции, формула применения билатерального фильтра находится как
решение Y следующей задачи:
E ( y)
n
( xn yn ) 2
ukn ( yk yn ) 2 min
kN r
(Eq. 1)
где зашумленное изображение X (с яркостями пикселей xi) приближается более гладким
изображениям Y (с яркостями пикселей yi).
Nr – окрестность радиуса r с центром в пикселе yn ( dist( yk yn ) r ), коэффициенты ukn – некоторые
постоянные.
A. Найдите отсюда yn - т.е. покажите, что уравнения для его вычисления имеет вид
w
1 w
xn
yn
nk y k
Nr
(Eq. 2)
nk
Nr
B. Выразите коэффициенты wkn в ((Eq. 2) через ukn и λ в ((Eq. 1):
C. Как мы обсуждали, билатеральный фильтр вычисляется итерационно:
y n(0) xn ,
w y
1 w
xn
y n( M 1)
(M )
nk k
Nr
nk
Nr
где М – номер итерации. Докажите, что такой фильтр инвариантен относительно равных
смещений яркости (shift-invariant): если мы увеличим все исходные xn на некоторую
постоянную δ, то все ynM увеличатся на нее же:
В чем, по-вашему, заключается практическое значение (и полезность) этого свойства?
D. *
Можете ли Вы предложить не-итерационное (но применимое на практике, т.е.
(Eq. 3)
эффективное) решение (Eq. 2), вместо (Eq. 3)? Явные решения системы (Eq. 2) не
предлагать: как было отмечено, у реальных изображений число точек (пикселей) может
достигать миллионов, и прямое обращение матрицы «миллион на миллион»
неосуществимо практически.
3 Применение билатерального фильтра
A. Напишите Matlab-программу BF.m, применяющую билатеральный фильтр для удаления
шума из томографического изображения. Используйте в ней окрестность Nr радиуса r=6, и
yn yk 2
wnk
e
2
1 dist 2 yn yk
где dist обозначает расстояние между пикселями yn и yk на плоскости. Используйте σ=200.
В качестве исходного изображения используйте DICOM-файл Low (снимок при низкой
радиационной дозе), а в качестве идеала, к которому надо стремиться при фильтровании – файл
High. Я прилагаю набросок программы в файле BF0.m, где уже определена функция LoadRData для
загрузки изображения. Вам надо написать функцию BFilter(L), которая берет изображение L,
фильтрует его, и возвращает как отфильтрованное F= BFilter(L). В качестве L берем Ims(:,:,2), а
отфильтрованное F сохраняем в Ims(:,:,3). Ims(:,:,1) содержит качественный сномок High.
Замените в BF0.m места с “TODO” на Ваш код. Не забудьте переименовать BF0.m в BF.m.
B. Пользуясь данной программой, профильтруйте изображение, используя одну итерацию в
(Eq. 3), и три разных значения λ: {0.01, 0.5, 2}. Программа должна показать три снимка
(High, отфильтрованный Low, Low) в один ряд. Скопируйте этот результат (три
профильтрованных снимка, показанных вместе в один ряд) как скриншот1 ниже, для
соответствующих значений λ:
a. λ=0.01
b. λ=0.5
1
Скриншот должен включать только сам снимок, и ничего более. Размер его настройте так, чтобы три
снимка занимали всю ширину страницы (между полями).
c. λ=2
C. Как отличаются эти три снимка по уровню гладкости их яркостей? Как это связано с
регуляризационным параметром λ в исходной постановке задачи ((Eq. 1)?
D. Пользуясь результатами с тремя λ выше, постарайтесь визуально подобрать оптимальное λ
так, что отфильтрованный с ним снимок Low стал бы как можно ближе к High. Сделайте это
как минимум одним из двух способов:
a. Меняя значение λ в BF.m, и сравнивая снимки визуально
b. * Реализовав некий численный метод для вычисления оптимального λ (включите
его код в BF.m, и опишите принцип его действия в поле ниже). Подсказка –
используйте качественное изображение High, и постарайтесь Вашим численным
методом найти такое λ, чтобы шум в отфильтрованном Low стал таким же, как в
High.
Независимо от способа a. или b., скопируйте ниже полученные при найденном Вами
оптимальном λ снимки (три скриншота в формате задания 3B выше)
λ=__________________:
E. *
Расчет билатерального фильтра занимает значительное время. Я поместил в программу
tic-toc для показа времени, но снимок маленький, и на больших данных все будет
значительно медленнее. Предложите какой-нибудь способ ускорения вычисления
значений фильтра.