Построение сечений многогранников

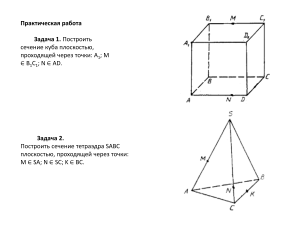
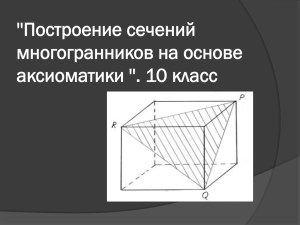
Земскова Людмила Николаевна учитель математики МБОУГимназия№4 г. Красноярск
Урок математики в 10 классе «Построение сечений многогранников»
Цели:
 формировать навыки решения задач на построение сечения многогранника;
 развивать пространственное воображение
Ход занятия:
Теоретическая часть.
I.

Знакомство с понятием сечения, виды сечения.
Если многогранник лежит по одну сторону от данной плоскости, то он может:
1. не иметь общих точек;
2. иметь одну общую точку – вершину многогранника;
3. иметь общий отрезок – ребро многогранника;
4. иметь общий многоугольник – грань многоугольника.
Если у многоугольника имеются точки, лежащие по разные стороны от данной
плоскости, то общей частью плоскости и многогранника будет многоугольник,
называемый сечением многогранника. (Показать на моделях).
Секущая плоскость пересекает грани многогранника по отрезкам. Многоугольник,
сторонами которого являются эти отрезки, называется сечением многогранника.
Так как тетраэдр имеет четыре грани, то его сечением может быть только
треугольник и четырехугольник. Параллелепипед имеет шесть граней. Его сечением
может быть: треугольник, четырехугольник, пятиугольник и шестиугольник.

Проверка знаний основных понятий данной темы
Математический диктант
1. Может ли в сечении куба плоскостью получиться:
а) треугольник;
б) правильный треугольник;
в) равнобедренный треугольник;
г) прямоугольный треугольник;
д) тупоугольный треугольник.
2. Может ли в сечении куба плоскостью получиться:
а) четырехугольник;
б) квадрат;
в) прямоугольник;
г) неравнобедренная трапеция;
д) прямоугольная трапеция.
3. Сколько диагональных сечений имеет n – угольная призма.
4. Опишите сечение куба плоскостью, имеющее наибольшую площадь.
5. Какие многоугольники можно получить в сечении четырехугольной
пирамиды плоскостью?
(Ответы на вопросы обсудить во фронтальной беседе с учащимися).

Формирование алгоритма построения сечения многогранника.
Учитель на примерах различных задач рассказывает, как строятся сечения
тетраэдра и параллелепипеда. Учащиеся делают соответствующие записи в
тетрадях. Рассказ учителя сопровождается показом слайдов.
(презентация 1)
II.
Отработка навыка построения сечений многогранников.
Работа в группах: (проверка и обсуждение решений через показ слайдов)
Деятельность учащихся
1. решение задач №1 -№4
2. защита решений (чертеж на доске)
3. обсуждение способов решения
задачи
4. проверка с помощью презентации
Деятельность учителя
Учитель консультирует учащихся, если у
них возникают затруднения при решении
задачи.
При обсуждении способов решений обратить особое внимание учащихся на тот факт, что
если секущая плоскость пересекает две противоположные грани параллелепипеда по каким-то
отрезкам, то эти отрезки параллельны. Следует обосновать это утверждение: плоскости
противоположных граней параллелепипеда параллельны, поэтому согласно утверждению 1 из
п. 11 секущая плоскость пересекает их по параллельным прямым.
Задача 1.
Дан тетраэдр ABCS. Построить сечение плоскостью, проходящей через точки M, N, K,
которые принадлежат соответственно ребрам SA, AC, SB.
Задача 2.
Дан тетраэдр ABCS. Построить сечение плоскостью, проходящей через точки M, N, К.
Точки М и N принадлежат соответственно ребрам SA, SC, а точка К принадлежит
плоскости АВС
Задача 3.
Построить сечение плоскостью проходящей через
точки А, В, С
А
B
C
Задача 4.
Построить сечение плоскостью проходящей через
точки А, В, С
B
А
C
III.
Итог урока.
Оценивание работы по группам.
Фронтальная беседа по готовым рисункам. Правильно ли выполнено сечение.
М
В
К
А
С
N
L б)
а)
P
P
A
B
A
B
г)
в)
C
C
IV.
Домашнее задание.
Записи в тетрадях, №72, № 73 (учебник Атанасяна Л. С. Геометрия 10 – 11)