Анализ результатов репетиционного экзамена по математике за

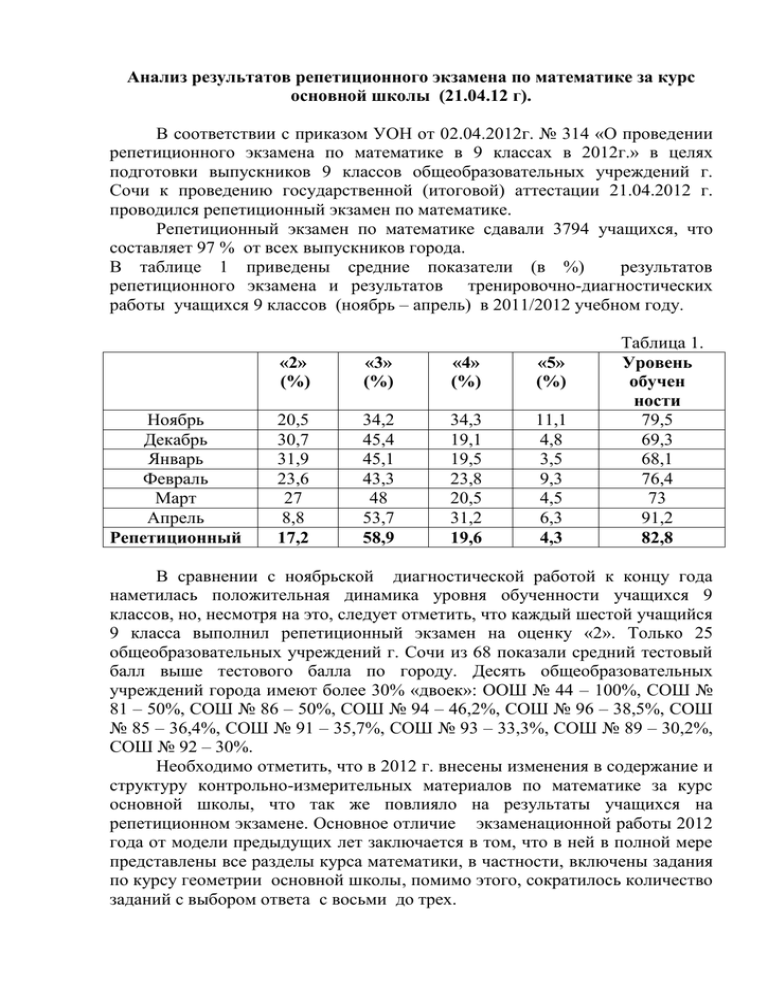
Анализ результатов репетиционного экзамена по математике за курс
основной школы (21.04.12 г).
В соответствии с приказом УОН от 02.04.2012г. № 314 «О проведении
репетиционного экзамена по математике в 9 классах в 2012г.» в целях
подготовки выпускников 9 классов общеобразовательных учреждений г.
Сочи к проведению государственной (итоговой) аттестации 21.04.2012 г.
проводился репетиционный экзамен по математике.
Репетиционный экзамен по математике сдавали 3794 учащихся, что
составляет 97 % от всех выпускников города.
В таблице 1 приведены средние показатели (в %)
результатов
репетиционного экзамена и результатов тренировочно-диагностических
работы учащихся 9 классов (ноябрь – апрель) в 2011/2012 учебном году.
Ноябрь
Декабрь
Январь
Февраль
Март
Апрель
Репетиционный
«2»
(%)
«3»
(%)
«4»
(%)
«5»
(%)
20,5
30,7
31,9
23,6
27
8,8
17,2
34,2
45,4
45,1
43,3
48
53,7
58,9
34,3
19,1
19,5
23,8
20,5
31,2
19,6
11,1
4,8
3,5
9,3
4,5
6,3
4,3
Таблица 1.
Уровень
обучен
ности
79,5
69,3
68,1
76,4
73
91,2
82,8
В сравнении с ноябрьской диагностической работой к концу года
наметилась положительная динамика уровня обученности учащихся 9
классов, но, несмотря на это, следует отметить, что каждый шестой учащийся
9 класса выполнил репетиционный экзамен на оценку «2». Только 25
общеобразовательных учреждений г. Сочи из 68 показали средний тестовый
балл выше тестового балла по городу. Десять общеобразовательных
учреждений города имеют более 30% «двоек»: ООШ № 44 – 100%, СОШ №
81 – 50%, СОШ № 86 – 50%, СОШ № 94 – 46,2%, СОШ № 96 – 38,5%, СОШ
№ 85 – 36,4%, СОШ № 91 – 35,7%, СОШ № 93 – 33,3%, СОШ № 89 – 30,2%,
СОШ № 92 – 30%.
Необходимо отметить, что в 2012 г. внесены изменения в содержание и
структуру контрольно-измерительных материалов по математике за курс
основной школы, что так же повлияло на результаты учащихся на
репетиционном экзамене. Основное отличие экзаменационной работы 2012
года от модели предыдущих лет заключается в том, что в ней в полной мере
представлены все разделы курса математики, в частности, включены задания
по курсу геометрии основной школы, помимо этого, сократилось количество
заданий с выбором ответа с восьми до трех.
На репетиционном экзамене 21.04.2012 года работа предлагалась в 6
вариантах, которые были составлены в соответствии с единой
спецификацией, и состояла из 2 частей, на выполнение которых учащимся
предлагалось 180 минут.
Часть 1 состояла из 18 заданий (из них 3 задания с выбором ответа, 14
заданий с кратким ответом и 1 – на установление соответствия между
объектами двух множеств) в совокупности охватывающих следующие
разделы курса: числа, буквенные выражения, преобразования алгебраических
выражений, уравнения, неравенства, числовые последовательности,
координаты на прямой и плоскости, функции и графики, элементы теории
вероятностей и статистики, геометрия. Часть 1 направлена на проверку
овладения содержанием курса на базовом уровне.
Часть 2, репетиционного экзамена, содержала 3 задания и была
направлена на проверку владения материалом на повышенном и высоком
уровнях.
При проверке работы за каждое правильно решенное задание 1 части
выставлялся 1 балл.
За выполнение заданий 2 части, учащийся получал установленный балл
(19 задание – 2 балла, 20 – 3 балла, 21 – 3 балла), или балл на 1 меньше
установленного (в случае если решение содержит несущественный недочет
или даже несущественную ошибку),
поэлементное оценивание не
предусматривалось. Максимальное количество баллов за работу составлял
18 × 2+3+3=26 баллов. Для положительной отметки ученик должен был
набрать 8 баллов из всей работы. В таблице 2 показана шкала оценивания
работ учащихся.
Отметка по
«2»
пятибалльной
шкале
Общий балл
Выполнено менее 8
заданий
«3»
«4»
Таблица 2.
«5»
8-14
баллов
15-21
баллов
22-26
баллов
Анализ выполнения Части 1 репетиционного экзамена.
В таблице 3 представлен процент выполнения заданий 1 части
учащимися на репетиционном экзамене.
Таблица 3.
№
1 2 3 4 5 6 7 8 9 10
задания
%
66 58 61 75 73 57 68 58 58 85
выполне
ния
11
12
13
14
15
16
17
18
63
49
51
44
33
42
64
34
Рассмотрим уровень выполнения заданий по блокам содержания.
Числа и вычисления. Задание 1 с кратким ответом типа «Найдите
значение выражения 4,2 1,8 . », проверяло умение выполнять действия с
6,3
десятичными дробями, с которым справилось 66 % учащихся, при этом на
диагностической работе
такое задание выполнило 83% учащихся. С
заданием 3 решение задач на проценты, например, «Вес тела на Луне
составляет 16% веса этого же тела на Земле. Сколько будет весить на Луне
космонавт, если на Земле весит 70 кг?» справилось 61% учащихся, в то
время, как на диагностической работе с задачей на проценты справлялось
73% учащихся. Из этого следует, что, как минимум, у 12 % выпускников
города не сформировано понятие процента. Учителям математики
необходимо обратить на это внимание и провести уроки обобщающего
повторения по теме «Проценты». Задание 5 с выбором ответов проверяло
умение учащихся решать задачи на сравнение (выполнило 73%).
Наибольшую трудность вызвали задания на сравнение квадратных корней с
натуральными числами, например: «Укажите наименьшее из чисел: 1) 8;
2)√60; 3) 3√6; 4) 4√5». В целом, по блоку «Числа и вычисления» учащиеся
показали не высокий уровень знаний. При организации повторения с
учащимися необходимо обратить внимание на темы: «Действия с
десятичными и обыкновенными дробями», «Решение задач на проценты».
Алгебраические выражения. В данном разделе было предложено задание 9
a  b a 2  b2
с кратким ответом типа «Упростите выражение
и найдите его
:
2
4
значение при a  3,2 и b   4,2 .». С задачами такого вида справилось только
половина учащихся города, что говорит о незнании формул сокращенного
умножения и проблемах с вычислительными навыками у учащихся.
Уравнения и неравенства. С задание 7 с кратким ответом, проверявшим
умение решать линейные уравнения, например, «Решите уравнение 2 (х +
1) – 6 = 4 (х – 2)», справилось 68% учащихся, что показывает на
непрочное усвоение учащимися алгоритма решения линейных уравнений.
Задание 18 проверяло умение решать квадратные неравенства «Решите
х 2  64  0 ». С заданиями такого типа справилось только
неравенство
34% учащихся, что говорит о неумении применять метод интервалов при
решении неравенств. С заданием 17 типа «Из формулы частоты обращения
N
n
выразите число полных оборотов N», проверявшим умение выражать
t
одну переменную через другую, справилось 64% учащихся. Подводя итог по
блоку уравнения и неравенства, можно отметить, что данная тема усвоена
учащимися города на невысоком уровне, особое внимание при обобщающем
повторении необходимо уделить теме «Решение неравенств».
Тема числовые последовательности была представлена заданием 13 и
проверяла
умение учащихся решать задачи на арифметическую и
геометрическую прогрессии, например, «Арифметическая прогрессия задана
несколькими первыми членами: 2; -1; -4… Найдите сумму первых десяти её
членов». Несмотря на то, что учащимся, предлагался справочный материал с
необходимыми формулами, с задачами такого типа справилось только 51%.
Это указывает на то, что выпускники 9 классов не умеют анализировать
текст задачи и выбирать необходимые для решения формулы.
Функции и графики. В данной теме задания 2 и 10 проверяли умение
читать графики и диаграммы реальных зависимостей. Задание 2 вида, «По
графику движения туристов определите, сколько часов потребовалось, чтобы
добраться до вершины горы?», выполнило 58% учащихся.
Задание 2 по уровню сложности посилен для слабых учащихся и при
правильной организации обучения решению этих задач можно достичь
лучшего результата.
Задание 10 на умение читать диаграммы выполнило 85% учащихся. С
заданием 12 на установление соответствия между объектами двух множеств,
например,
«Установите соответствие между графиками функций и формулами, которые
их задают.»
1
2
1) у = - х +3
2) у = ( х – 3 )2 – 4
1
0 1
x
4) у = х + 2
y
y
y
1
3) у = 2х + 2
1
x
0 1
x
0 1
а)
б)
в)
справилось 49% учащихся.
Координаты на прямой и плоскости. Задание 4 с кратким ответом на
сравнение чисел на координатной прямой вида,
На координатной прямой отмечены числа a и b .
a
0
b
Из следующих выражений выберите верное. 1. a  b  0
ba  0
2.
2a
b
0
3.
4. b  a  0 , выполнило 74% учащихся. Задание 16 на умение
находить координаты точки на плоскости выполнило только 42% учащихся.
Геометрия. Геометрические задачи в первой части репетиционного экзамена
были представлены 4 заданиями. Задание 6 на нахождение расстояний
(выполнило 57, 1%),например, «Используя данные, приведенные на рисунке
найдите высоту мачты АВ».
Задание 8 проверяло умение находить элементы в прямоугольном
треугольнике, умение применять знание свойств центральных и вписанных
углов при решении задачи (справилось 58,3%), например,
В треугольнике АВС угол C равен 90°, CH – высота, угол A равен 34°.
Найдите угол BCH.
Задание 14 вида «Одна из сторон параллелограмма равна 12, другая равна 5,
а один из углов —
. Найдите площадь параллелограмма.» выявляло
умение учащихся находить площади плоских фигур (выполнило 44,1%),
Задание 15 с выбором ответа проверяло знание теоретических вопросов из
курса планиметрии (выполнило 32,9%). Например.
Укажите номера верных утверждений.
1) Через любую точку плоскости можно провести прямую.
2) Через любую точку плоскости можно провести единственную прямую.
3) Существует точка плоскости, через которую можно провести прямую.
4). Через точку, не лежащую на данной прямой, можно провести на
плоскости не более одной прямой, параллельной данной.
5). Существует точка плоскости, через которую нельзя провести ни одной
прямой.
Подводя итог по блоку геометрических задач, который первый год был
включен в экзаменационные материалы, следует отметить, что учащиеся на
недостаточном уровне овладели знаниями по курсу планиметрии. Учителям
при организации уроков повторения по геометрии необходимо обратить
внимание на следующие темы:
 применение теоремы Пифагора;
 применение свойств подобных треугольников;
 тригонометрические функции углов;
 формулу расстояния между точками на координатной плоскости;
 теоремы о сумме углов треугольника и о внешнем угле
треугольника;
 свойства углов при параллельных прямых;
 теорему о сумме углов выпуклого многоугольника;
 свойства углов, вписанных в окружность;
 таблицы тригонометрических функций;
 формулу углов между векторами на координатной плоскости;
 формулу углов между прямыми на координатной плоскости.
 формулы
площади
треугольника,
прямоугольника,
параллелограмма, ромба, трапеции, круга и его частей;
 свойства площадей подобных фигур.
Задание 11 проверяло умение решать простейшие вероятностные задачи.
Необходимо было вычислить вероятность события по частоте. «Катя, Настя,
Игорь, Даша и Андрей бросили жребий – кому начинать игру. Найдите
вероятность того, что начинать игру должен будет мальчик» уровень
выполнения данных заданий составил 63,2%.
Подводя итоги выполнения заданий 1 части необходимо отметить, что по
десяти заданиям из 18 учащиеся города выполнили задания на уровне 60% и
ниже. К ним относятся:
 интерпретация графиков реальных зависимостей;
 действия с алгебраическими дробями;
 соотнесение графика функции с ее формулой;
 арифметическая и геометрическая прогрессии;
 решение квадратного неравенства;
 нахождение координаты точки на плоскости;
 геометрические задачи.
С тремя заданиями справились 65 – 85 % писавших выпускников:
 действия с десятичными дробями;
 сравнение чисел на координатной прямой;
 чтение диаграмм реальных зависимостей.
Рекомендации учителям по содержанию:
 провести уроки обобщающего повторения по теме: «Проценты»,
«Решение линейных уравнений и неравенств», «Действия с
алгебраическими дробями», «Интерпретация графиков реальных
зависимостей», «Функции», «Формулы сокращенного умножения»;
 обратить внимание на работу по закреплению вычислительных
навыков учащихся (например, с помощью устной работы на уроках:
применение арифметических законов действий при работе с
рациональными числами), что позволит успешно выполнять
задания, избегая досадных ошибок;
 особое внимание обратить на преподавание геометрии, включив в
повторение темы по которым учащиеся, по результатам
репетиционного экзамена, испытывают затруднение;
 для отработки заданий первой части кафедра физикоматематических дисциплин рекомендует использовать тренажер для
подготовки к ГИА, расположенный на сайте ККИДППО
www.idppo.kubannet.ru в разделе кафедра физико-математических
дисциплин.
Рекомендации по организации работы с учащимися:
 на дополнительных занятиях для отработки навыков счета можно
привлечь учителей начальных классов или учителей математики, не
работающих в выпускных классах;
 выделить «проблемные» 3-4 темы в каждом конкретном классе и
работать над ликвидацией пробелов в знаниях и умениях по этим
темам, по мере достижения уровня выполнения заданий до 85-90%
подключать другие темы;
 с учащимися, имеющими большие пробелы в знаниях, в первую
очередь закрепить достигнутые успехи, предоставляя им
возможность на каждом уроке
выполнять 15-20 минутную
самостоятельную работу, в которую включены задания на
отрабатываемую тему, по мере усвоения добавлять в
самостоятельную работу новые задания;
 определить индивидуально для каждого учащегося перечень тем, по
которым у них есть хоть малейшие продвижения, и работать над их
развитием;
 с учащимися, имеющими хорошие знания, помимо ежеурочной
тренировки в решении задач базового уровня сложности (в виде
самостоятельных работ), проводить разбор методов решения задач
повышенного уровня сложности, проверяя и усвоение этих методов
на самостоятельных работах и дополнительных занятиях.
Задания для подготовки учащихся к итоговой аттестации можно найти
в текстах краевых диагностических работ прошлых лет, в открытой базе
ГИА на сайте www.mathgia.ru/ , а также в учебных пособиях по подготовке к
ГИА.
1. Математика: ГИА: Учебно-справочные материалы для 9 класса.
(Серия «Итоговый контроль: ГИА») / Л.В. Кузнецова, С.Б. Суворова и др. /
М.; СПб.: Просвещение, 2012.
2. Тематический сборник тестовых заданий по алгебре для подготовки
к государственной (итоговой) аттестации в новой форме. Базовый уровень. /
Под редакцией Е.А. Семенко. – Краснодар: Просвещение-Юг, 2008.
3. Тематический сборник заданий по алгебре для подготовки к
государственной (итоговой) аттестации в новой форме. Повышенный
уровень. / Под редакцией Е.А. Семенко. – Краснодар: Просвещение-Юг, 2008
Методист ОЕМиТО СЦРО
С.В. Исаева