Инструкция по проведению районной диагностической работы (РДР) № 4
реклама

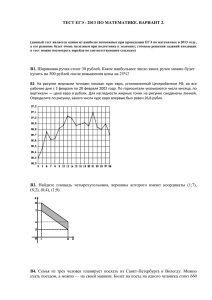
Инструкция по проведению районной диагностической работы (РДР) № 4 по математике в 11 классе Тема: ПРОИЗВОДНАЯ. ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ. СВОЙСТВА И ГРАФИК ФУНКЦИИ . Цель: -отследить уровень усвоения учащимися следующих тем: 1. Определение производной и техника дифференцирования; 2. Геометрический и физически смысл производной; 3. Применение производной для исследования свойств функции (монотонность, экстремумы, наибольшее и наименьшее значения) и построения ее графика; 4. Практическое применение производной; 5. Применение свойств функций при решении уравнений, неравенств; 6. Графический метод решения уравнений, неравенств, а так же задач с параметрами. - планомерная подготовка к ЕГЭ 2013 года по математике. Задачи: 1. Планомерная подготовка учащихся к написанию ЕГЭ. 2. Проявление пробелов в знаниях учащихся, с целью дальнейшего их устранения. 3. Ознакомление учащихся с особенностями ЕГЭ по математике. О проведении работы: 1. Работа состоит из 2 частей: 1 часть (задания В1 – В6) – базовый (общеобразовательный) уровень, задания формулируются на языке ЕГЭ, 2 часть (С1 – С2) состоит из заданий аналогичных тем, которые раньше требовались при поступлении в технические ВУЗы. Используемые материалы при составлении работы: задания открытого банка (mathege.ru) и задания различных сборников по подготовке к поступлению во ВТУЗы, а также разработки ФИПИ и др.. 2. Время написания работы: 45 минут (1 урок). 3. Система оценивания работы: 1). За верное выполнение заданий части 1 учащийся получает 1 балл. 2). За любое неверное выполнение задания части 1 - 0 баллов. 3). Оценивание заданий 2 части: С1 – от 0 до 2 баллов, С2 – от 0 до 4 баллов (см. также критерии оценивания). Максимальный балл за всю работу – 12 баллов. Использование калькуляторов, сотовых телефонов, а также справочных материалов запрещается. Таблица перевода баллов в традиционную оценку: Набранный балл менее 3 баллов 3 – 5 баллов 6 – 8 баллов 9 и выше баллов Оценка 2 3 4 5 Вариант 1. Часть 1 Ответом на задания В1 — В6 является целое число или конечная десятичная дробь. Единицы измерений писать не нужно. В1. На рисунке изображен график y f x — производной функции f x , определенной на интервале 17;2 . Найдите количество точек минимума функции f x , принадлежащих отрезку 12;1 . В2. На рисунке изображён график функции y f x и шесть точек на оси абсцисс: x1 , x2 ,, x6 . В скольких из этих точек производная функции f x положительна? В3. На рисунке изображён график функции y f x . Пользуясь рисунком, вычислите F (6) F (2) , где F (x) — одна из первообразных функции f x . В4. Найдите наибольшее значение функции отрезке В5. . на В6. Для получения на экране увеличенного изображения лампочки в лаборатории используется собирающая линза с главным фокусным расстоянием см. Расстояние от линзы до лампочки может изменяться в пределах от 55 до 70 см, а расстояние от линзы до экрана — в пределах от 260 до 300 см. Изображение на экране будет четким, если выполнено соотношение . Укажите, на каком наименьшем расстоянии от линзы можно поместить лампочку, чтобы еe изображение на экране было чeтким. Ответ выразите в сантиметрах. Часть 2 Задания С1 ― С2 выполняются с полным обоснованным решением и с записью ответа. С1. а) Решите уравнение 5 б) Найдите все корни этого уравнения, принадлежащие отрезку 4 ; 2 С2. Найдите все значения a, при каждом из которых уравнение имеет единственный корень. Вариант 2. Часть 1 Ответом на задания В1 — В6 является целое число или конечная десятичная дробь. Единицы измерений писать не нужно. В1. На рисунке изображен график y f x — производной функции f x , определенной на интервале 5;15 . Найдите количество точек максимума функции f x , принадлежащих отрезку 0;14 . В2. На рисунке изображён график функции y f x и десять точек на оси абсцисс: x1 , x2 ,, x10 . В скольких из этих точек производная функции f x отрицательна? В3. На рисунке изображён график функции y f x . Пользуясь рисунком, вычислите F (5) F (3) , где F (x) — одна из первообразных функции f x . В4. Найдите наименьшее значение функции на отрезке . В5. В6. Для получения на экране увеличенного изображения лампочки в лаборатории используется собирающая линза с главным фокусным расстоянием f 45 см. Расстояние от линзы до лампочки может изменяться в пределах от 50 до 70 см, а расстояние от линзы до экрана — в пределах от 160 до 180 см. Изображение на экране будет четким, если выполнено соотношение . Укажите, на каком наименьшем расстоянии от линзы можно поместить лампочку, чтобы еe изображение на экране было чeтким. Ответ выразите в сантиметрах. Часть 2 Задания С1 ― С2 выполняются с полным обоснованным решением и с записью ответа. С1. а) Решите уравнение 3 б) Найдите все корни этого уравнения, принадлежащие отрезку ;3 2 С2. Найдите все значения a, при каждом из которых уравнение имеет единственный корень. Вариант 3. Часть 1 Ответом на задания В1 — В6 является целое число или конечная десятичная дробь. Единицы измерений писать не нужно. В1. На рисунке изображен график y f x — производной функции f x , определенной на интервале 10;12 . Найдите количество точек минимума функции f x , принадлежащих отрезку 9;10 . В2. На рисунке изображён график функции y f x и восемь точек на оси абсцисс: x1 , x2 ,, x8 . В скольких из этих точек производная функции f x положительна? В3. На рисунке изображён график функции y f x . Пользуясь рисунком, вычислите F (6) F (2) , где F (x) — одна из первообразных функции f x . В4. Найдите наибольшее значение функции на отрезке . В5. . В6. Для получения на экране увеличенного изображения лампочки в лаборатории используется собирающая линза с главным фокусным расстоянием f 50 см. Расстояние от линзы до лампочки может изменяться в пределах от 60 до 80 см, а расстояние от линзы до экрана — в пределах от 120 до 150 см. Изображение на экране будет четким, если выполнено соотношение . Укажите, на каком наименьшем расстоянии от линзы можно поместить лампочку, чтобы еe изображение на экране было чeтким. Ответ выразите в сантиметрах. Часть 2 Задания С1 ― С2 выполняются с полным обоснованным решением и с записью ответа. С1. а) Решите уравнение 7 б) Найдите все корни этого уравнения, принадлежащие отрезку 2 ; 2 С2. Найдите все значения a, при каждом из которых уравнение имеет единственный корень. Вариант 4. Часть 1 Ответом на задания В1 — В6 является целое число или конечная десятичная дробь. Единицы измерений писать не нужно. В1. На рисунке изображен график y f x — производной функции f x , определенной на интервале 12;8 . Найдите количество точек максимума функции f x , принадлежащих отрезку 8;7 . В2. На рисунке изображён график функции y f x и двенадцать точек на оси абсцисс: x1 , x2 ,, x12 . В скольких из этих точек производная функции f x отрицательна? \ В3. На рисунке изображён график функции y f x . Пользуясь рисунком, вычислите F (7) F (5) , где F (x) — одна из первообразных функции f x . В4. Найдите наименьшее значение функции отрезке на . В5. В6. Для получения на экране увеличенного изображения лампочки в лаборатории используется собирающая линза с главным фокусным расстоянием f 60 см. Расстояние от линзы до лампочки может изменяться в пределах от 100 до 120 см, а расстояние от линзы до экрана — в пределах от 120 до 140 см. Изображение на экране будет четким, если выполнено соотношение . Укажите, на каком наименьшем расстоянии от линзы можно поместить лампочку, чтобы еe изображение на экране было чeтким. Ответ выразите в сантиметрах. Часть 2 Задания С1 ― С2 выполняются с полным обоснованным решением и с записью ответа. С1. а) Решите уравнение log 3 sin x sin 2 x 27 3. 7 ;2 . б) Найдите все корни этого уравнения, принадлежащие отрезку 2 С2. Найдите все значения a, при каждом из которых уравнение имеет единственный корень. Ответы и критерии оценивания заданий части 2. Ответы: Задание С1 С2 Вариант 1 2 а ) к; 2к 3 10 8 б ) 4 ; ;3 ; 3 3 2 2 а ; a0 3 7 а) Вариант2 к; 1к 1 2 6 3 11 5 б) ; ; 2 6 2 4 a 0; a4 9 к а) Вариант 3 к; 1к Вариант 4 к 2 6 13 5 17 7 б) ; ; ; 6 2 6 2 2 2 а ; a0 3 7 а) к; 2к 3 7 б ) 3 ; ;2 3 1 1 а ; a 0 3 Примечание: Уважаемые коллеги, во избежание недоразумений, проверьте ответы. С уважением Васильев Г.Г.. Критерии: Задание С1 баллы 2 1 0 содержание критериев Верное и обоснованное решение Верно решен один из пуктов а) или б); допущена вычислительная ошибка, но решение доведено до ответа (возможно не верного) Во всех остальных случаях Задание С2 4 3 2 1 0 Верное и обоснованное решение Допущена вычислительная ошибка; рассмотрены все возможные случаи, но в ответе некоторые значения были утеряны; не достаточно обосновано построение графика Указаны все возможные случаи, но полностью верно разобран только один случай или ошибки при построении графика Существенное продвижение в решении, например: неверно построен график (грубые ошибки при построение, но алгоритм решения ученик знает) Во всех остальных случаях С уважением методисты ИМЦ по математике!