Задания для 7В класса по геометрии. Решить задачи по готовым
реклама

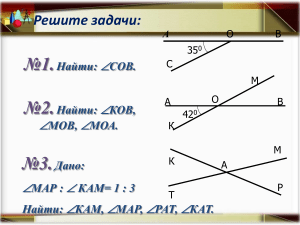
Задания для 7В класса по геометрии. 1. Решить задачи по готовым чертежам ( см. ниже), в тетради для домашней работы. Таблица 7.3 с 1-4 устно, с 5-10 письменно. Таблица 7.4 с 1-4 устно, с 5 -8 письменно. Задания для 7А,В классов по геометрии. Проверочный тест (выполнить в тетради для домашней работы) 1. Точка С лежит на луче АВ. Какая из точек А, В, С лежит между двумя другими? а) А; б) В или С; в) С; г) В. 2. Отрезок ХМ пересекает прямую а. Отрезок ХD пересекает прямую а. Пересекает ли прямую а отрезок МД? а) да; б) может не пересекать; в) никогда не пересекает; г) нет правильного ответа. 3. Один из углов, образованных при пересечении двух прямых,- прямой. Остальные углы… а) Острые и прямой; б) тупые и прямой; в) прямые; г) нет правильного ответа. 4. Сумма двух углов, образованных при пересечении двух прямых, равна 180 градусам. Эти углы: а) Смежные; б) вертикальные; в) нет правильного ответа; г)могут быть смежными, могут быть вертикальными. 5. Если точка В принадлежит отрезку АС, то… а) АВ+ВС=АС; б) АВ +АС=ВС; в) ВС+АС=АВ; г) нет правильного ответа . 6. Если луч ОС проходит между сторонами угла АОВ, то… а) <АОС=<ВОС; б) <АОС+<ВОС=<АОВ; г)<АОС+<АОВ=<ВОС. в) <АОВ+<ВОС=<АОС; 7. Если точка В- середина отрезка АС, то… а) АВ+ВС=АС; б) АС=ВС; в) АВ=2АС; г) АС=2АВ. 8. Луч ОС- биссектриса угла АОВ, то а) <АОВ=<АОС+<ВОС; б) <АОС=<АОВ; в) <АОС=<ВОС; г) <АОВ‡<ВОС. Самостоятельная работа. 1. Точка С- середина отрезка АВ, точка D- середина отрезка АС, ВD=15,3 см. Найдите длину отрезка АС и выразите ее в миллиметрах. 2. Отрезки РЕ и НМ лежат на перпендикулярных прямых и пересекаются в точке К. Внутри угла РКН взята точка А, а внутри угла МКЕ- точка В, <АКН=40°, <МКВ=50°. а) Найти углы РКА и ВКЕ. б) Лежат ли точки А, К, В на одной прямой? 3. Развернутый угол АОВ разделяет плоскость на две части. Луч ОМ лежит в одной части, а луч ОК – в другой. Известно что углы МОА и КОВ- прямые. а) Равны ли углы ВОМ и КОА? б) Являются ли прямые МК и АВ взаимно перпендикулярными? 4. Можно ли расположить 6 точек на 4-х отрезках, не лежащих на одной прямой, так, чтобы каждому отрезку принадлежало по три точки? 5. Расположите шесть отрезков так, чтобы каждый из них имел общие точки ровно с тремя другими и число всех этих точек было равно пяти. ТЕТРАДИ С РЕШЕНИЯМИ ПО ОКОНЧАНИЮ АКТИРОВАННЫХ ДНЕЙ СДАТЬ УЧИТЕЛЮ МАТЕМАТИКИ ШАРАПОВОЙ С.Г.