Раздел 1. Теория статистики
реклама
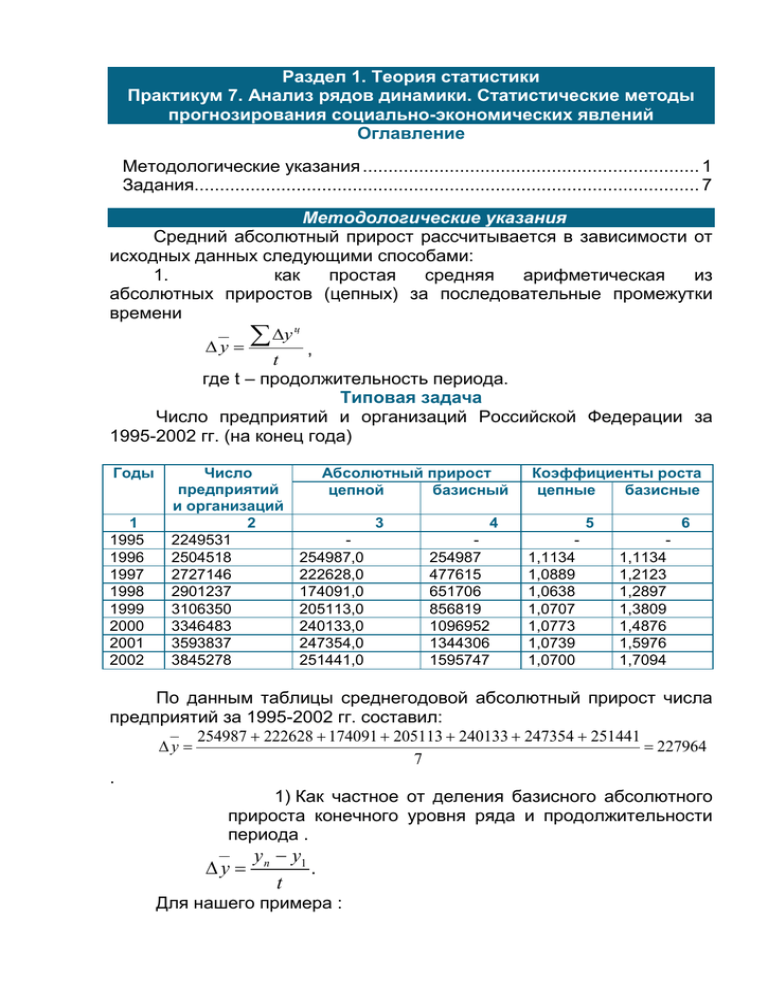
Раздел 1. Теория статистики Практикум 7. Анализ рядов динамики. Статистические методы прогнозирования социально-экономических явлений Оглавление Методологические указания .................................................................. 1 Задания................................................................................................... 7 Методологические указания Средний абсолютный прирост рассчитывается в зависимости от исходных данных следующими способами: 1. как простая средняя арифметическая из абсолютных приростов (цепных) за последовательные промежутки времени y ц y , t где t – продолжительность периода. Типовая задача Число предприятий и организаций Российской Федерации за 1995-2002 гг. (на конец года) Годы 1 1995 1996 1997 1998 1999 2000 2001 2002 Число предприятий и организаций 2 2249531 2504518 2727146 2901237 3106350 3346483 3593837 3845278 Абсолютный прирост цепной базисный 3 254987,0 222628,0 174091,0 205113,0 240133,0 247354,0 251441,0 Коэффициенты роста цепные базисные 4 254987 477615 651706 856819 1096952 1344306 1595747 5 1,1134 1,0889 1,0638 1,0707 1,0773 1,0739 1,0700 6 1,1134 1,2123 1,2897 1,3809 1,4876 1,5976 1,7094 По данным таблицы среднегодовой абсолютный прирост числа предприятий за 1995-2002 гг. составил: 254987 222628 174091 205113 240133 247354 251441 y 227964 7 . 1) Как частное от деления базисного абсолютного прироста конечного уровня ряда и продолжительности периода . y y n y1 . t Для нашего примера : 3845278 2249531 227964 . 7 Через накопленный (базисный) абсолютный прирост (Δуб): y y б y . t Для нашего примера (графа 4) Δуб2002= 1595747. 1595747 227964 . Тогда y 7 Средний коэффициент роста (снижения) показывает, во сколько раз в среднем за единицу времени изменяется уровень ряда динамики. Для вычисления среднего коэффициента роста используется формула геометрической средней. В зависимости от наличия исходных данных расчет проводится следующим образом: 1. если исходной информацией служат цепные коэффициенты роста, то формула имеет вид: K t K1ц K 2ц ... K3ц t ПK ц , где "П" означает произведение цепных показателей динамики. Для нашего примера K 7 1,1134 1,0889 1,0638 1,0707 1,0773 1,0739 1,07 7 1,7094 1,0796 . 2. Через базисный конечного периода: коэффициент роста б K t K конечного периода . Для нашего примера графа 6 Кб2002= 1,7094, тогда K 7 1,7094 1,0796 . 3. Если известны уровни динамического ряда: K t yn y1 . Для нашего примера: 3845278 K 7 1,7094 1,0796 . 2249531 Средний темп роста представляет собой средний коэффициент роста, выраженный в процентах (T K 100 ). Соответственно, средний темп прироста равен: T T 100 . Для нашего примера число предприятий в России с 1995 по 2002 гг. увеличивались в среднем на 7,96% в год. Метод скользящей средней состоит в том, что расчет средних уровней по укрупненным интервалам проводится путем последовательного смещения начала отсчета на единицу времени, т.е. постепенно исключаются из интервала первые уровни и включаются последующие. Рассмотрим условный пример: уi – объем чистой ссудной задолженности коммерческого банка. Год Фактические уровни ряда уi, млн. руб. Сглаженный уровень (скользящие средние) yt 1994 1995 1996 1997 1998 1999 2000 2001 2002 2003 2004 500 550 602 644 729 810 896 956 1084 1168 1300 , млн. руб. 550,7 598,7 658,3 727,7 811,7 887,3 978,7 1069,3 1184,0 - Для имеющегося ряда динамики имеем: 500 550 602 y1 550,7млн. руб. 3 y5 729 810 896 811,7млн. руб. 3 550 602 644 598,7млн. руб. 3 810 896 956 887,3млн. руб. 3 y2 y6 y3 602 644 729 658,3млн. руб. 3 896 956 1084 978,7млн. руб. 3 644 729 810 727,7млн. руб. 3 y7 y4 y8 y9 956 1084 1168 1069,3млн. руб. 3 1084 1168 1300 1184,0млн. руб. 3 Метод аналитического выравнивания состоит в построении аналитической функции, характеризующей зависимость уровней ряда от времени. Расчет параметров значительно упрощается, если за начало отсчета времени (t=0) принять середину ряда динамики. При нечетном числе уровней в нашем примере получим такие значения t: Годы t 1994 -5 1995 -4 1996 -3 1997 -2 1998 -1 1999 0 2000 1 2001 2 2002 3 2003 4 2004 5 При четном числе уровней: Годы t 1994 -4,5 1995 -3,5 1996 -2,5 1997 -1,5 1998 -0,5 1999 0 2000 0,5 2001 1,5 2002 2,5 2003 3,5 2004 4,5 В обоих случаях Σt=0. Тогда система уравнений принимает вид: y an 2 . y t b t Отсюда: a b y ; n y t 0 t 2 . t Результаты расчетов представим в таблице Год 1 1994 1995 1996 1997 1998 1999 2000 уi 2 500 550 602 644 729 810 896 t2 t 3 -5 -4 -3 -2 -1 0 1 4 25 16 9 4 1 0 1 у∙t 5 -2500 -2200 -1806 -1288 -729 0 896 y t a bt 6 444 523 602 682 761 840 919 2001 2002 2003 2004 Итого 956 1084 1168 1300 9239 a 2 3 4 5 0 4 9 16 25 110 1912 3252 4672 6500 8709 998 1078 1156 1236 9239 9239 8709 839,9млн.руб. ; b 79,2млн.руб. . 11 110 y t 839,9 79,2t . На основе найденного уравнения рассчитываются выравненные уровни, соответствующие во времени фактическим уровням ряда динамики (графа 6 таблицы). Наиболее часто употребляемый метод измерения сезонных колебаний – это так называемый "индекс сезонности". В стационарных рядах динамики расчет индекса сезонности состоит в определении простой средней арифметической за одни и те же внутригодовые промежутки времени всего изучаемого периода. Затем полученные средние сопоставляются с общей средней динамического ряда. Формула расчета: is yi 100, y где y i - средний уровень по одноименным внутригодовым отрезкам времени (месяцам, кварталам). При наличии тренда, т.е. в нестационарных рядах динамики, порядок расчета индекса сезонности следующий: 1. По одноименным внутригодовым уровням ряда (месячным, квартальным) за ряд лет определяют расчетные (выравненные) уровни ( y t ) при помощи скользящей средней или методом аналитического выравнивания. 2. Определяется процентное отношение фактических уровней ряда (уi) и расчетных (выравненных) уровней. 3. Получение показателей сезонности усредняются за все годы. Упрощенная формула расчета индекса сезонности для нестационарных рядов динамики выглядит так: y i is 100 : n. y t Рассмотрим порядок расчета индекса сезонности на условном примере. При внутригодовом планировании деятельности сберегательных учреждений необходимо учитывать, что вклады населения подвержены сезонным колебаниям, которые могут быть вызваны сезонностью отпусков, сезонным характером экономической деятельности в сельской местности и т.п. Допустим, по результатам выборочного обследования счетов физических лиц коммерческого банка были получены следующие данные об изъятии вкладов, представленные в таблице: Расчет индексов сезонности изъятия вкладов в коммерческом банке. Год Квартал Объем выданных вкладов, млн. руб., уi Скользящие четырехквартальные 2001 2002 2003 I II III IV I II III IV I II III IV 3,42 3,54 5,38 3,38 3,78 3,88 5,90 3,72 4,10 4,24 6,44 4,06 средние, 3,98 4,06 4,17 4,28 4,36 4,45 4,56 4,67 - Индекс сезоннос ти, % yt 135,18 83,25 90,65 90,65 135,32 83,60 89,91 90,79 - Для получения обобщенной оценки сезонности за весь период нужно рассчитать средние показатели сезонности за каждый квартал. Расчет оформим в таблице. Расчет средних индексов сезонности объема изъятия вкладов в коммерческом банке Кварталы I II III IV Средний индекс сезонности, % ( i s ) 90,65 89,91 90,28 2 90,65 90,79 90,72 2 135,18 135,22 135,25 2 83,25 83,60 83,43 2 На графике явно выражен период максимального изъятия вкладов – это третий квартал и минимального изъятия вкладов – это четвертый квартал. Задания Задача 1 Основные статьи актива баланса коммерческого банка региона по кварталам. Млн. руб. 04.01.03 01.07.03 5 01.01.03 4 01.10.02 3 01.07.02 2 Денежные средства и счета в ЦБ РФ Государственные долговые обязательства Средства в кредитных организациях Вложения в ценные бумаги для перепродажи Ссудная задолженность 01.04.02 1 01.01.02 Вар-т Активы 67,3 105,8 120,1 89,6 112,4 154,2 113,1 54,0 47,5 47,5 49,6 55,1 58,1 42,3 75,3 211,3 169,9 170,4 82,7 316,2 502,7 6,7 24,2 31,2 25,1 7,6 10,1 12,74 158,9 177,0 201,2 250,1 264,4 299,4 273,1 На основе соответствующих вашему варианту данных определить: 1. Цепные и базисные показатели динамики: абсолютный прирост, темп роста, темп прироста. 2. Средний уровень ряда динамики. 3. Средний абсолютный прирост, средний темп роста, средний темп прироста. 4. Произвести сглаживания ряда динамики трехлетней скользящей (подвижной) средней. 5. Изобразить фактический и выравненный ряды графически. Задача 2 Исходные данные по Российской Федерации Вариант Показатели 1 Число предприятий и организаций на конец года Число малых предприятий на конец года, тыс. Удельный вес убыточных предприятий % от общего числа предприятий Рентабельность проданных товаров и активов организаций (%) ВВП млн руб (до 1998г – млрд) 2 3 4 5 1997 1998 1999 2000 2001 2002 2003 2727146 2901237 3106350 3346483 3593837 3845278 4149815 861,1 868 890,6 879,3 843 882,3 890,9 50,1 53,2 40,8 39,8 37,9 43,5 43,0 6,3 8,1 18,5 18,9 14,4 10,9 10,2 2228584,3 2424047,7 4149289,6 6219253,8 7741381,3 9409991,8 11582339,7 На основе соответствующих вашему варианту данных требуется 1. Рассчитать показатели динамики и сделать выводы о тенденции развития уровней динамического ряда. 2. Обоснуйте выбор уравнения тренда и определите его параметры. 3. Определите прогнозное значение для тренда, продленного на единицу времени. Задание 3 Имеются данные о потреблении электроэнергии (квт-час) в одной семье по кварталам. Квартал 1 2 3 4 2004 г. 574 354 306 422 2005г. 588 380 304 532 2006 г. 600 384 368 524 Требуется: 1. Рассчитать индексы сезонности. 2. Построить график индекса сезонности. 3. Объяснить полученные результаты. Задание 4 Имеются данные, характеризующие ввод в эксплуатацию жилых домов в городе за счет всех источников финансирования за 19992004 гг. Ввод в эксплуатацию жилых домов за счет всех источников финансирования, тыс. кв. м. общей площади. 1999 2000 2001 2002 2003 2004 1073 1081 1118 1213,7 1757,9 2032 Коэффициент роста (по отношению к предыдущему году) 1,007456 1,034228 1,085599 1,448381 1,155925 Абсолютный прирост (по сравнению с предыдущим годом) 8 37 95,7 544,2 274,1 Требуется: 1. Определить средние показатели динамики, используя разные способы расчета. 2. Объяснить полученные результаты. Задание 5 Имеются данные о динамике цен на первичном рынке жилья по отдельным регионам страны: %% Российская Федерация Центральный федеральный округ Белгородская область Брянская область Владимирская область Воронежская область Ивановская область Калужская область Первичный рынок жилья 1997 1999 2000 2001 2002 115,3 146,3 113,1 125,1 122,5 2003 118,8 103,5 154,8 105,1 116,8 123,1 124,1 106,1 133,5 116,9 120,9 139,1 118,4 99,0 96,5 129,3 123,8 103,6 119,2 115,5 138,4 142,8 126,4 130,9 140,7 99,0 119,2 101,4 112,7 118,5 123,7 131,9 114,5 131,5 135,8 120,9 91,6 133,5 126,1 114,3 110,0 161,3 На основе данных варианта, который устанавливается для конкретного региона, требуется: 1. Определить базисный коэффициент роста цен за 2000-2003 гг. 2. Рассчитать средний темп прироста цен за 1997-1999 гг. и за 2000-2003 гг. 3. Рассчитать показатели, указанные в п.1 и п. 2 по данным индексов цен страны в целом. 4. Сравнить полученные результаты.

