Документ 777664

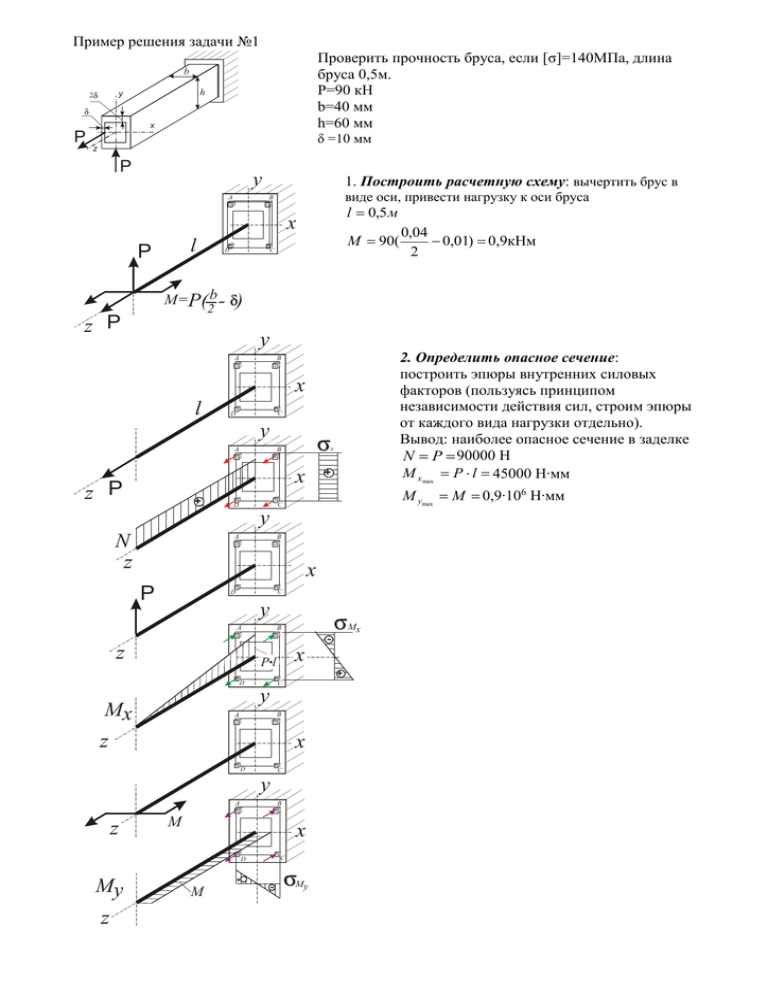
Пример решения задачи №1
Проверить прочность бруса, если [σ]=140МПа, длина
бруса 0,5м.
P=90 кН
b=40 мм
h=60 мм
b
h
у
2
х
P
δ =10 мм
z
P
y
1. Построить расчетную схему: вычертить брус в
виде оси, привести нагрузку к оси бруса
B
A
l  0,5 м
x
l
P
M=P( b -
y
2. Определить опасное сечение:
построить эпюры внутренних силовых
факторов (пользуясь принципом
независимости действия сил, строим эпюры
от каждого вида нагрузки отдельно).
Вывод: наиболее опасное сечение в заделке
N  P  90000 Н
M x max  P  l  45000 Н∙мм
B
A
x
l
C
D
y
B
A
N
+
x
z P
+
M ymax  M  0,9∙106 Н∙мм
C
D
y
N
z
B
A
x
P
C
D
y
A
z
Mx
B
x
Pl
+
D
C
y
Mx
z
B
A
x
D
C
y
B
A
z
M
x
+
D
My
z
M
0,04
 0,01)  0,9кНм
2
)
2
z P
M  90(
C
D
C
My
При данной форме сечения можно сразу указать
опасные точки
y
N
A
B
Mx
N
Mx
x
My
+
+
+
D
C
My
3. В опасном сечении определить
опасную точку:
Для того, чтобы определить опасную
точку в сечении любой
геометрической формы необходимо:
1) построить нейтральную линию; 2)
провести прямые параллельные
нейтральной линии и касательные к
контуру сечения.
Точки касания –точки наиболее
удаленные от нейтральной линии опасные точки.
Наибольшее растягивающее напряжение в точке D,
наибольшее сжимающее – в точке B
Построение нейтральной линии:
а) Определяем геометрические характеристики сечения:
Площадь поперечного сечения A= b  h  (b  2 )  (h  4 )  40∙60-20∙20=2000мм2
Момент инерции сечения относительно оси x
(когда балка изгибается в вертикальной плоскости, все её сечения поворачиваются относительно оси x.
Момент инерции сечения показывает насколько легко можно повернуть сечение данной геометрической
формы относительно этой оси – т.е. определяет жесткость балки)
b  h3 (b  2 )  (h  4 )3 40  603 20  203
=720000-13333,3=706666,7мм4



12
12
12
12
h
Расстояние от оси x до наиболее удаленной от нее точки сечения ymax=  30мм
2
Момент инерции сечения относительно оси y
h  b3 (h  4 )  (b  2 )3 60  403 20  203
Iy 



 320000-13333,3=306666,7мм4
12
12
12
12
Ix 
(момент инерции относительно y меньше, значит и сечение развернуть легче – меньше жесткость в этом
направлении)
b
 20мм
2
б) Составляем уравнение нейтральной линии.
Составим уравнение по которому можно определить
Mx
N
напряжение в любой точке опасного сечения – для
x
этого возьмем точку, координаты которой
y
+
положительны (чтобы знак координаты не
+
накладывался на знак напряжения). Знаки
напряжений в этой точке берем с эпюр напряжений.
N M y M x
My
  x  y .
A
Ix
Iy
Чтобы найти напряжение в любой точке сечения, достаточно подставить в это уравнение
координаты точки с соответствующим знаком. Если подставить в это уравнение координаты
точки, лежащей на нейтральной линии, то напряжение будет равно 0.
Получаем уравнение нейтральной линии:
M x
N M y
90000 45000  yн 900000  xн
н   x н  y н 


 45  0,064 yн  2,9 xн  0
A
Ix
Iy
2000 706666,7 306666,7
Решая уравнение получим: при x=0 y=703мм; при y=0 x=15,5мм
Строим сечение в масштабе, находим положение нейтральной линии и опасных точек
Расстояние от оси y до наиболее удаленной от нее точки сечения xmax 
y
+
x
н. л
Максимальное растягивающее напряжение в точке D
M x
N M y
h
b
 D   x D  y D  45  0,064( )  2,9( ) 
A
Ix
Iy
2
2
45  0,064  30  2,9  29  131М31     140МПа
Максимальное сжимающее напряжение в точке B
M x
N M y
h
b
 B   x B  y B  45  0,064   2,9  
A
Ix
Iy
2
2
B
A
45  0,064  30  2,9  29  41МПа
 B     140МПа
Условие прочности выполняется.
C
D
+
B
D
Задача №2
Дано:
a=55мм
b=90мм
l=260мм
d1=145мм
d2=295 мм
N=8кВт
ω=30,5об/с
   70МПа
Для промежуточного вала двухступенчатого редуктора
требуется: а) построить эпюру крутящих моментов,
эпюры изгибающих моментов в вертикальной и
горизонтальной плоскостях, эпюру продольных сил; б)
определить требуемый диаметр вала. Расчет вести по
гипотезе наибольших касательных напряжений.
Принять T=0,37P; A=0,14P.
Полученное по расчету значение диаметра (в мм)
округлить
до
ближайшего
большего
числа,
оканчивающегося на 0; 2; 5; 9.
1. Представить вал в виде оси. Перенести
к оси все нагрузки
260
90
YB
XB
55
260
90
55
0,37P1
P1
2
1
0,14P2
0,37P2
N  M 
Передаваемый валом момент равен:
N 8000
M  
 262,3Н  м
 30,5
Из условия равновесия вала относительно оси Z
следует:
Z
0,37P1
0,14P2
YA
P2
P2 d 2
2
B
P
1
P2
XA
YB
XB
Z
d1
B
2
YA
A
ZA
P
1
0,37P2
0,14P2
P1
d1
P2 d 2
XA
2
d2
A
2
262,3
262,3
 3593,2 Н ; P2 
 1772,3Н
0,073
0,148
T=0,37P; T1  0,37 P1  1329,5Н ;
T2  0,37P2  655,8Н
A=0,14P; А2  0,14P2  248,1Н
При переносе осевой силы А к оси,
возникает изгибающий момент
d
0,295
A2 2  248,1
 36,6 Н  м
2
2
P
1
ZA
2
d1
d
d
0,145
 P2  2  M ; P1  1  P1 
 262,3 ;
2
2
2
2
d
0,295
P2  2  P2 
 262,3
2
2
P1 
P1 
260
90
YB
XB
55
Z
1329,5Н
248,1Н
YA
B
1772,3Н
XA
A
ZA
3593,2Н
262,3Нм
655,8Н
36,6Нм
262,3Нм
2. Определить опасное сечение. Для этой цели, пользуясь принципом независимости действия
нагрузок, рассмотреть отдельно каждый вид деформаций
YB
262,3Нм XB
Z
B
262,3Нм
YA
XA
P1
A
Мкр
ZA
Первый вид деформации – кручение.
Момент 262,3Нм закручивает участок вала между первым
и вторым колесом.
Второй вид деформации – сжатие.
 FZ  Z A  248,1  0 ; Z A  248,1Н
Третий вид деформации – изгиб в вертикальной
плоскости.
 M A  1329,5  0,055  655,8  0,145  36,6  YB  0,26  0
1329,5  0,055  36,6  655,8  0,145
 56,3H
0,26
 M B  36,6  655,8  0,115 1329,5  0,205  YA  0,26  0
YB 
1329,5  0,205  36,6  655,8  0,115
 617,4 H
0,26
Проверка:
 FY  132,9  655,8  YB  YA  0
YА 
YB
XB
262,3Нм
Z
YA
XA
Y
N
ZA
_
A
115
248,1Н
90
55
YB =56,3Н
36,6Нм
Z
1329,5Н
B
3593,2  0,055  1772,3  0,145
 1748,5H
0,26
 M B  1772,3  0,115  3593,2  0,205  X A  0,26  0
XB 
3593,2  0,205  1772,3  0,115
 3617 H
0,26
Проверка:
 FX  1772,3  3593,2  X B  X A  0
XА 
YA=617,8Н
655,8Н
A
MX
34Нм
6,5Нм
115
XB=1748,5Н
90
B
55
1772,3Н
XA =3617Н
3593,2Н
MY
201Нм
199Нм
F
 1772,3  3593,2  1748,5  3617  0
Суммарный момент изгибающий
X
M из  M X2  M Y2
В сечении под первым колесом момент изгибающий
равен:
30,1Нм
A
F
 1329,5  655,8  56,3  617,4  0
Эпюры моментов изгибающих располагают со стороны
сжатого волокна.
Четвертый вид деформации – изгиб в горизонтальной
плоскости
 M A  3593,2  0,055 1772,3  0,145  X B  0,26  0
B
248,1Н
M из  34 2  199 2  201,9 Нм
В сечении под вторым колесом момент изгибающий
равен:
M из  30,12  2012  203,2 Нм
Наиболее опасно сечение под вторым колесом.
Условие прочности при изгибе с кручением имеет вид:

М из2  М кр2
0,1d 3
   ;
103  203,2 2  262,32
 70 ;
0,1d 3
103  311,8
 70 . Определяем диаметр вала:
0,1d 3
d  10  3
311,8
 35,5 мм ; Примем d=39мм
0,1  70
Задача №3
Растет на сопротивление усталости. Усталостное разрушение обычно происходит при напряжениях в
несколько раз меньших, чем предельные. Причинами такого разрушения являются: динамический характер нагрузки
(циклически изменяющаяся нагрузка) и реакция материала детали на такую нагрузку, наличие концентраторов
напряжения (шпоночные канавки, проточки, сверления, резкий перепад размеров), упрочнение поверхности и др.
Расчет выполняют в форме проверки коэффициента S запаса прочности, .минимально допустимое значение
которого принимают в диапазоне [S] = 1,5 - 2,5.
S
S S
S  S
2
2
 S ; S 
 1
K
 a    m
 
; S 
 1
K
 
 a   m
Проверочный расчет на усталостную прочность выполним только для сечения вала под зубчатым
колесом. Концентратором напряжения в этом сечении является шпоночный паз.
Нормальные напряжения изменяются по ассимметричному циклу:
N 248,1
248,1
=0,21МПа;


2
d
392
A


4
4
M
203,2 103 203,2 103
амплитудное напряжение -  a  из 
=34,3МПа;

Wиз
0,1d 3
0,1 393
среднее напряжение -  m 
Касательные

напряжения
изменяются
по
пульсирующему
(отнулевому)
циклу
-
Mк
262,3 10
262,3 10


 11,1МПа
3
2 Wк  2
0,2d  2
0,2  393  2
 1  230МПа ;  1  135МПа - пределы выносливости гладких образцов выбранного материала – даны
m  a 

3
3
в условии задачи.
Для углеродистых сталей    0,10 ,    0,20 - коэффициенты чувствительности материала к
асимметрии цикла.
K и K - коэффициенты учитывающие влияние концентратора напряжений.
Значения K и K для валов со шпоночной канавкой принимаем по графику.
Например, для  пч  530МПа примем K =1,68 и K =1,57
  и  - масштабные факторы. Т.е. коэффициенты, учитывающие влияние на усталостную
прочность размеров детали.
Значения   и  примем в соответствии с графиком
Для d=39мм и  пч  530МПа примем   =  =0,8
 - коэффициент учитывающий влияние шероховатости поверхности. При Ra  0,32  2,5 мкм
принимают   0,97  0,90 . Примем   0,97 - дано в условии задачи
230
135
=3,1; S 
=5,7;
S 
1,68
1,57
34,3  0,2  0,21
11,1  0,111,1
0,8  0,97
0,8  0,97
3,1 5,7
S
 2,7  2,5 - Усталостная прочность вала обеспечена.
3,12  5,7 2