Метод использования вычислительной техники и её возможностей для приближенного нахождения корня

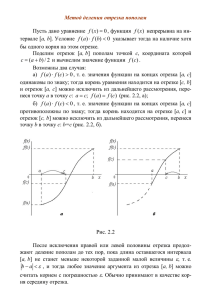
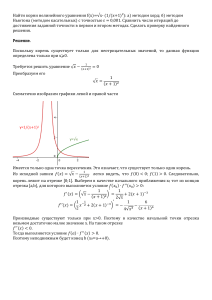
Министерство науки и высшего образования Российской Федерации
Федеральное государственное бюджетное образовательное учреждение
высшего образования
«Алтайский государственный технический университет им. И.И. Ползунова»
Факультет информационных технологий
Кафедра информационных технологий
Отчёт защищён с оценкой
Преподаватель
(подпись)
«
Е.М.Гельфанд
(и.о. фамилия)
»
2024 г.
Отчёт по лабораторной работе №1
«Решение нелинейных уравнений с одной неизвестной»
по дисциплине «Численные методы»
Вариант - 20
Студент группы
ИСП-22
К. В. Чернаков
Преподаватель
Е. М. Гельфанд
БАРНАУЛ 2024
В данной лабораторной работе нам требуется решить трансцендентное
уравнение 3 * ln2 x + 6 * ln x -5 с заданной точностью 0.001, найдя его корень
на указанном промежутке [1; 3]
Первый метод.
Метод использования вычислительной техники и её возможностей для
приближенного нахождения корня
Строим график функции с помощью сайта для построения диаграмм
yotx.ru
Рисунок 1 – График функции
2
Из данной картинке видно, что корень данного уравнения находиться
на промежутке от [1,8;1,9]
Для нахождения шага из конечной координаты вычитаем начальную и
делим это на 10 шагов. Соответственно шаг будет равен (1,9 – 1,8)/10 =0,1
Рисунок 2 – Точки первого отрезка
Считая на отрезке от точки 1,8 до точки 1,9 вычислив 10 шагов, мы
обнаружили смену знака, после чего мы на этом отрезке перестаём считать.
Делаем следующую итерацию уменьшая данный отрезок до [1,88;1,89].
Следующий шаг будет равен (1,89 – 1,88)/10 =0,01
Рисунок 3 – Точки второго отрезка
Считая на отрезке от точки 1,88 до точки 1,89 вычислив 5 шагов, мы
обнаружили смену знака после чего мы на этом отрезке перестаем считать.
Делаем следующую итерацию уменьшая данный отрезок до [1,883;1,884].
Следующий шаг будет равен (1,884 – 1,883)/10 =0,0001
3
Рисунок 4 – Точки третьего отрезка
Считая на отрезке от точки 1,883 до точки 1,884 вычислив 4 шага, мы
обнаружили смену знака после чего мы на этом отрезке перестаем считать.
Так как наши вычисления в точке 1,8832 и в точке 1,8833 оказались меньше
заданной точности. Находим корень как среднее арифметическое границ, где
у нас выполняется точность.
Первый этап лабораторной работы выполнен. Найден корень х = 1.883.
4