Численное решение уравнений Метод половинного деления
реклама

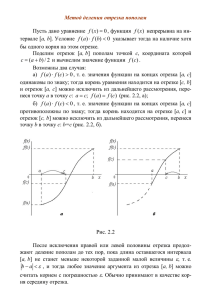
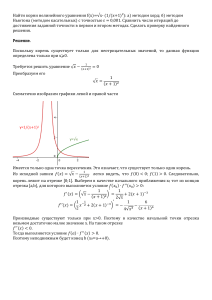
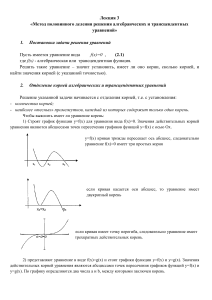
Косаренко Нина, 10 класс МОУ СОШ п.Донское Численное решение уравнений Метод половинного деления 2006 г. f(x) = 0 (1) Рассмотрим функцию у = f(x) на отрезке [a; b ] Если f(x) – непрерывная и монотонная на отрезке [a; b] функция, то утверждение о том, что уравнение (1) имеет на отрезке [ a; b] единственный корень равносильно тому, что f(a)*f(b)<0 При этом если изобразить график функции y=f(x), то кривая графика будет пересекать ось Ох в точке , которая и будет являться корнем уравнения (рис. 1). Рисунок 1. Для нахождения корня отрезок [a; b] делится пополам (рис.2) Рисунок 2. хi = а +(b-а)/2 – и выбирается тот полуинтервал, на концах которого знаки f(х) разные. Для определения знаков функции достаточно вычислить ее значение в точках a, xi и b соответственно. Полученные значения сравниваются следующим образом: 1. Если одно из найденных значений равно нулю, т. е. f(a) = 0 or f(xi) = 0 or f(b) = 0, то найден соответствующий корень уравнения. Процесс прекращается. 2. Если (f(a) > 0 and f(xi) < 0) or (f(a) < 0 and f(xi) > 0), то корень находится на отрезке [a, xi]. Примечание Это сложное условие легко заменяется более простым. А именно, с учетом правил действия со знаками в математике легко записать: если (f(xn)*f(xi) < 0), то ... . Действительно, при умножении чисел с разными знаками всегда получается отрицательное число. Тогда пункт 2: Если (f(xi) > 0 and f(b) < 0) or (f(xi) < 0 and f(b) > 0), то корень находится на отрезке [xi, b] заменим условием: если (f(xi)*f(b) < 0), то... . Рисунок 3 Если длина выбранного отрезка еще не стала меньше некоторого наперед заданного числа ε – точности вычислений (т. е. в нашем случае | b-xi | < ε), то процесс деления отрезка пополам повторяется уже для нового отрезка. Пусть дано уравнение: 5sin(2x-1)-0,7=0. Найдем корни уравнения, принадлежащие отрезку [1;10]. Решать задачу будем в 2 этапа: Выделим отрезки, на которых уравнение имеет единственный корень Методом деления пополам найдем корни на каждом из выделенных отрезков. 1. Чтобы выделить отрезки, на которых уравнение имеет единственный корень, разобьем отрезок на [1;10] малые отрезки (длиной 0,1) и на каждом из отрезков проверим условие: f(xi)*f(xi+1)<0, где [xi ; xi+1] - один из отрезков. Все отрезки, для которых условие выполняется, будем выводить на экран. Программа выделения отрезков Результат работы программы (найденные отрезки): Программа, реализующая метод половинного деления : Окно выполнения: Результаты работы программы (найденные корни): на [2;2.1]: на [3.7;3.8]: на [5.1;5.2]: на [6.8;6.9]: на [8.2;8.3]: на [9.9;10]: x = 2,000488 ≈ 2 x = 3,711719 ≈ 3,71 x = 5,141406 ≈ 5,14 x = 6,853907 ≈ 6,85 x = 8,283594 ≈ 8,28 x = 9,994531 ≈ 9,99 Таким образом, мы приближенно решили данное уравнение на отрезке [1 ;10] с точностью 0.001 методом половинного деления.