Методы оптимизации

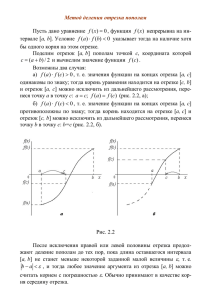
МЕТОДЫ
ОПТИМИЗАЦИИ
§ 1. Основные понятия
Под оптимизацией понимают
процесс выбора наилучшего варианта
из всех возможных
В процессе решения задачи оптимизации
обычно необходимо найти оптимальные значения
некоторых параметров, определяющих данную задачу.
При решении инженерных задач их принято называть
проектными параметрами,
а в экономических задачах их обычно называют
параметрами плана.
Выбор оптимального решения или
сравнение двух альтернативных решений
проводится с помощью
некоторой зависимой величины (функции),
определяемой проектными параметрами.
Эта величина называется целевой функцией
(или критерием качества).
u  f  x1 , x2 , , xn 
В процессе решения задачи оптимизации
должны быть найдены такие значения
проектных параметров, при которых
целевая функция имеет минимум (или максимум).
Задачи оптимизации.


Безусловная задача оптимизации состоит в отыскании
максимума или минимума действительной функции от n
действительных переменных и определении
соответствующих значений аргументов
Условные задачи оптимизации, или задачи с
ограничениями, — это такие, при формулировке которых
задаются некоторые условия (ограничения) на множестве.
Теория и методы решения задач оптимизации
при наличии ограничений
составляют предмет исследования
одного из важных разделов прикладной математики —
математического программирования.
§ 2. Одномерная оптимизация
Одномерная задача оптимизации в общем случае
формулируется следующим образом:
Найти наименьшее (или наибольшее)
значение целевой функции у = f(x),
заданной на множестве 
и определить значение проектного параметра
x 
при котором целевая функция принимает
экстремальное значение.
Существование решения поставленной задачи
вытекает из следующей теоремы:
Теорема Вейерштрасса.
Всякая функция f(x), непрерывная на отрезкеa,b 
принимает на этом отрезке наименьшее и наибольшее
значения, т. е. на отрезке a,b 
существуют такие точки
x1 и x2
что для любогоx  a ,b
имеют место неравенства
f  x1   f  x   f  x2 
.
Методы поиска.
Численные методы поиска экстремальных значений
функции рассмотрим на примере нахождения
минимума функции f(x) на отрезкеa,b 
Будем предполагать, что целевая функция
унимодальна,
т. е. на данном отрезке она имеет только один минимум.
Погрешность приближенного решения задачи определяется
разностью между оптимальным значением х
проектного параметра и приближением к нему x
Потребуем, чтобы эта погрешность была
по модулю меньше заданного допустимого значения
x  x  
Процесс решения задачи методом поиска
состоит в последовательном сужении
интервала изменения проектного параметра,
называемого интервалом неопределенности
В начале процесса оптимизации его длина равна b – a,
а к концу она должна стать меньше
т. е. оптимальное значение проектного параметра
должно находиться в интервале неопределенности —
отрезке xn , xn  1 
причем xn  1  xn  
Тогда для выполнения условия
x  x  
в качестве приближения к оптимальному значению
можно принять любое
x  xn , xn  1 
x  xn
Например,
или x  xn  1 , или x   xn  xn  1  / 2
В последнем случае достаточно выполнения неравенства
xn  1  xn  2
Метод золотого сечения.
Метод состоит в построении
последовательности отрезков
a0 ,b0  , a1 ,b1,…,
 стягивающихся к точке минимума
функции f(x).
На каждом шаге, за исключением первого,
вычисление значения функции f(x)
проводится лишь в одной точке.
Эта точка, называемая золотым сечением,
выбирается специальным образом.
1 шаг
внутри отрезка a0 ,b0 
выбираем некоторые внутренние точки
x1
и
x2
и вычисляем значения целевой функции
f  x1 
и
f  x2 
f  x3 
f  x2 
f  x1 
a0
x1
f  x1 
x2
b0
a1  a0
x3
x1
b1  x2
Поскольку в данном случае
f  x1  < f  x2 
очевидно, что минимум расположен
на одном из прилегающих к x1
отрезков:
a0 ,x1 
или x1 ,x2 
Поэтому отрезок x2 ,b0 
можно отбросить, сузив тем самым
первоначальный интервал неопределенности.
Второй шаг
проводим на отрезкеa1 ,b1 
a1  a0 b1  x2
Нужно снова выбрать две внутренние точки,
но одна из них
x1
где
осталась из предыдущего шага,
поэтому достаточно выбрать лишь одну точкуx3
вычислить значение f  x3 
и провести сравнение.
Поскольку здесь
f  x3  < f  x1 
ясно, что минимум находится на отрезке
x3 ,b1 
Обозначим этот отрезокa2 ,b2 
снова выберем одну внутреннюю точку
и повторим процедуру сужения
интервала неопределенности.
Процесс оптимизации повторяется до тех пор,
пока длина очередного отрезка
ak ,bk 

не станет меньше заданной величины
Теперь рассмотрим способ размещения внутренних точек
на каждом отрезке
ak ,bk 
Пусть длина интервала неопределенности равна l,
а точка деления разбивает его на части
l1 ,
l2 >
l1
l2
l  l1  l2
Золотое сечение интервала неопределенности
выбирается так, чтобы отношение длины
большего отрезка к длине всего интервала
равнялось отношению длины меньшего отрезка
к длине большего отрезка:
l1 l2

l l1
Из этого соотношения можно найти точку деления,
вычислив отношения
l2
l1


l
l
Преобразуем выражение и найдем значения

l12  l2 l
2
l1
 l1 
   1  0
l
l 
и
l12  l l  l1 

l12  l1l  l 2  0
  1  0
2
1 5

2
Поскольку нас интересует только положительное решение, т
1 5
3 5

 0.618
  1 
 0.382
2
2
Очевидно, что интервал неопределенности можно
разделить в соотношении золотого сечения двояко:
в пропорциях
l2 : l1
и
l1 : l2
x1  a0 l2
В данном случае имеем b  a  l  
0
0
x1  a0   b0  a0 
x1  1   a0  b0
x1  a0  b0
Аналогично,
x2  a0  b0
Начальная длина интервала неопределенности составляет
d0  b0  a0
После первого шага оптимизации получается
новый интервал неопределенности — отрезок
a1 ,b1 
Его длина равна
d 1  b1  a1  x2  a0  a0  b0  a0   b0  a0   d 0  0.618 d 0
На втором шаге отрезок
a1 ,b1 
также делится в соотношении золотого сечения.
При этом одной из точек деления будет точка x1
Покажем это:
x1  a0  b0  a0   1  

 

x2  a0  b0  a0  

Последнее равенство следует из соотношения
 2  1  0
Вторая точка деления x3
выбирается так же, как выбирается точкаx1
при делении отрезка a0 ,b0 
т. е. x3  a1  b1
И снова интервал неопределенности
уменьшается до размера
d 2  b2  a2  b1  x3  b1  a1  b1   b1  a1   d1   2 d0
По аналогии можно записать координаты
точек деления у и z отрезка
ak 1 ,bk 1 
на к-м шаге оптимизации (у < z):
y  ak  1  bk  1
z  ak 1  bk 1
Вычислению, естественно,
подлежит только одна из координат у, z
другая координата берется с предыдущего шага.
При этом длина интервала неопределенности равна
d k  bk  ak   k d0  0.618 k d0
Как и в общем случае метода поиска,
процесс оптимизации заканчивается
при выполнении условия
dk  
Тогда проектный параметр оптимизации
x  ak ,bk 
В качестве приближения к оптимальному значению
можно принять
ak  bk 
x  ak или x  bk , или x 
2
В последнем случае для достижения
требуемой точности достаточно, чтобы
d k  2