Нескучная математика для детей

/ИЛ
Анна Андреева
о Я о
ego
12 14 26
15 18 33
19 11
?
• Математические, логические
и геометрические задачи
• Задачи со спичками
• Магические квадраты и кроссворды
• Числовые и буквенные ребусы
НЕСКУЧНАЯ
МАТЕМАТИКА
ДЛЯ ДЕТЕЙ
ОТ 10 ЛЕТ
Санкт-Петербург
«БХВ-Петербург»
2018
УДК 51:373.34
ББК 22.1я71
А65
А65
Андреева А. О.
Нескучная математика для детей от 10 лет. - С П б .: БХВ-Петербург,
2018. - 160 с.: ил. - (Развивающие головоломки)
ISBN 978-5-9775-3963-0
Книга содержит разнообразные занимательные задания и способ­
ствует развитию логики, аналитических и математических способно­
стей, памяти, внимания и сосредоточенности у детей от 10 лет. Все
задания объединены по темам: магические квадраты, задания со
спичками, логические, математические и геометрические задачи,
кроссворды, ребусы и другие нескучные вопросы.
Приводятся примеры решений, краткие теоретические справки,
разъяснения новых слов и понятий. Ответы на все задания даны в
конце книги.
Детям книга поможет содержательно провести свободное время,
более успешно усвоить школьную программу и участвовать в мате­
матических олимпиадах и конкурсах, учителям - проводить занима­
тельные уроки и дополнительные занятия, родителям - интересно
организовать совместный досуг.
УДК 51:373.34
ББК 22.1я71
Группа подготовки издания:
Главный редактор
Зам. главного редактора
Зав.редакцией
Редактор
Корректор
Компьютерная верстка
и дизайн обложки
Екатерина Кондукова
Л ю дм ила Еремеевская
Екатерина Капалыгина
А нна Кузьмина
Зинаида Дмитриева
М арин ы Д а м би ев о й
«БХВ-Петербург», 1 9 1 0 3 6 , Санкт-Петербург, Гончарная ул., 20.
ISBN 9 7 8 - 5 - 9 7 7 5 - 3 9 6 3 - 0
© Андреева А. О ., 2 0 1 8
© Оформление. ООО «БХВ-Петербург», ООО «БХВ», 2 0 1 8
СОДЕРЖАНИЕ
ДОРОГИЕ ДРУЗЬЯ!
6
РАЗМИНКА
7
Задачи на внимательность
7
Задачи на закономерности
9
Кроссворд, кейворд, филворд
13
Расстановки,маршруты
18
Спички
21
Спичкиифигуры
21
Спички и числа
24
Спички и слова
26
Римскиечисла
28
Арифметические выражения
с римскими числами
29
Спички и равенства
31
Разныезадачисоспичками
32
м а г и ч е с к и е квад раты
34
Построение магических квадратов
34
Магические квадраты 3x3, 5x5, 7x7
40
3
ГЕОМЕТРИЧЕСКИЕ ЗАДАЧИ
Расстановка фигур на доске
42
Геометрическиефигуры
44
Количество кубиков в фигуре
46
Задачи с кубиками
48
Составление квадратов
и прямоугольников
50
Разрезаниефигур
52
Расстановка чисел
54
Деление фигуры на равные части
56
Подсчёт прямоугольников,
треугольников и квадратов
58
ДЕЛИМОСТЬ
60
Признакиделимости
60
Составлениечисел
62
р а в е н с т в а , к а р т о ч к и , р еб ус ы
4
42
67
Знакиарифметическихдействий
67
Числа на карточках
71
Числовыеибуквенныеребусы
72
ЗАКОНОМЕРНОСТИ
76
Числа последовательности
76
Закономерности в числовых ребусах
79
Чётность
85
Чётныеинечётныечисла
85
Может — не может
86
РАЗНЫЕ ЗАДАЧИ
96
Задуманноечисло
96
Наибольшееинаименьшеечисла
97
Выпавшиестраницы
98
Кошки-мышки
100
Неотрываякарандашаотбумаги
102
Разделение линиями
и окружностями
105
Соответствия
106
Тяжёлое-лёгкое
113
Логическиезадачи
114
О тв еты
117
л и тература
148
5
д о р о ги е д р уз ь я !
Решая задачи, которые собраны в этой
книге, вы разовьёте сообразительность,
внимание, математические способности
и сосредоточенность, получите прекрас­
ную возможность интересно проводить
время с друзьями, родителями, братья­
ми или сёстрами, сможете подготовить­
ся к конкурсам и олимпиадам или просто
блеснуть знаниями. Здесь есть и задания
со спичками, и магические квадраты,
и задания на развитие логики, матема­
тические, и даже геометрические зада­
чи. Справиться с задачами вам помогут
«напоминалки» по теории, разъяснения
новых слов и понятий и примеры реше­
ний. Ответы к заданиям тоже есть (они
в конце книги), а к некоторым даже по­
яснения.
Ус п е х о в !
б
разм инка
з а д а ч и н а в н и м ател ь н о с ть
Сколько колец серого цвета изображе­
но на рисунке?
7
2
8
Какой робот отличается от остальных?
разм инка
з а д а ч и на з ак о н о м ер н о с ти
Выберите рисунок, который должен
стоять вместо вопросительного знака.
а)
1.
2.
3.
4.
5.
б)
1.
2.
3.
В - <$> П
10
4.
5.
<*> В
разм инка
Какое число стоит вместо вопроситель­
ного знака?
11
5
12
Определите, какое число соответствует
каждой игрушке.
РАЗМИНКА
кроссворд, КЕЙВОРД, филворд
КРОССВОРД (от Английского СЛОВА
CROSSWORD - п е р е с е ч е н и е слов) гол ов о л о м ка , В которой ряды КЛЕточЕК
п е р е п л е т е н ы . э т и к л е т о ч к и над о
з а п о л н и ть с л о в а м и по з а д а н н о м у
описанию .
КЕйворд, или ключворд - это
кроссворд, в котором о д и н ако в ы м
б уквам с о о тв етс тв ую т одинаковы е
числа.
Филворд - это р а з н о в и д н о с т ь к р о с с в о р д а .
и г р о к у д а н а с е т к а с б у к в а м и и несколько
слов, к о т о р ы е н а д о о т ы с к а т ь в с е т к е .
р а з г а д ы в а т ь н а д о к а к по в е р т и к а л и , т а к и
по г о р и з о н т а л и . с л о в а м о г у т и з г и б а т ь с я .
к а ж д а я б у к в а п р и н а д л е ж и т только о д н о м у
слову
13
Числа замените буквами так, чтобы
получились математические термины
и слова. Одинаковые числа означают
одинаковые буквы. Воспользуйтесь под­
сказкой.
5
8
1
2
2
2
10
6
3
17
14
9
7
14
17
5
5
10
16
7
10
5
4
8
9
1
5
3
11
11
8
2
3
16
7
5
8
7
16
2
15
2
3
5
8
1
2
3
2
2
2
4
3
12
3
3
15
14
11
2
13
17
13
15
2
16
10
7
16
5
3
9
13
10
6
2
10
1
10
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
т Р И
14
РАЗмИнКА
В таблице найдите слова
ДЕЛИТЕЛЬ ПРОПОРЦИЯ МАТЕМАТИКАЛОГИКА
СЛОЖЕНИЕ ЗАДАЧА ГРАДУС ПАРАЛЛЕЛЕПИПЕД
7
МЕРА ЧИСЛО УГОЛ ТРЕУГОЛЬНИК ОБЪЁМ
Слова написаны в различных направ­
лениях, изгибаются под прямым углом.
и
Л
Е
Д
Я
И
ц
Р
т
Е
Л
л
О
А
т
О
л
О
ь
А
Г
М
и
п
с
И
ч
К
и
Е
к
о
м
Е
с
М
А
Т
А
р
А
Р
л
А
Д
А
3
п
Е
Ж
О
Ч
А
Г
Р
А
Н
И
т
Р
Е
У
У
Д
П
Е
ь
Л
О
г
с
У
А
Р
н
И
К
л
О
Г
Л
А
Е
П
Е
дм
Ё
Л
Е
Л
И
П
О
Б
Ъ
15
Ответьте на вопросы и впишите подхо­
дящие слова.
Цифра.
Геометрическаяфигура.
Частьпрямой.
Арифметическоедействие.
Сумма всех сторон прямоугольника.
Единица измерения углов.
Число.
8 . Знакарифметическогодействия.
9.
Инструментдля построения окруж­
ностей.
10. Делимое,делитель,...
1.
2.
3.
4.
5.
6.
7.
1
2
3
4
5
6
7
8
9
10
іб
М
А
Т
Е
М
А
Т
И
к
А
РАЗМИНКА
Расставьте слова.
УРАВНЕНИЕ ПРОПОРЦИЯ ДРОБЬ ЧИСЛО
ГРАФИК ВЫЧИТАНИЕ УМНОЖЕНИЕ КРУГ
РАДИУС Л О Г И К А СЕМЬ
Из букв в закрашенных клетках со­
ставьте слово, означающее число.
Л
0
г
и
к
А
17
р а с с т а н о в к и , м арш руты
10
18
Дорожки в саду расположены так, как
показано на рисунке. Смотритель сада
расставил три фонаря. Как можно уста­
новить ещё четыре фонаря так, чтобы
все дорожки были освещены? Фонари
освещают те дорожки, на пересечении
которых установлены.
РАЗМИНКА
В здании 50 комнат. Коле нужно соста­
вить маршрут так, чтобы оказаться в каж­
дой комнате только один раз и при этом
пройти все помещения. Как Коля может
это сделать?
19
Семь кошельков расставлены так, как
показано на рисунке. Как разложить
98 монет в кошельки так, чтобы в двух
соседних кошельках количество отлича­
лось бы на 3 монеты?
20
спички
го I
□
I
I___ J
спички и ФИГУРЫ
Солнце составлено из
12 спичек. Переложите
б спичектак, чтобы полу­
чилось б треугольников.
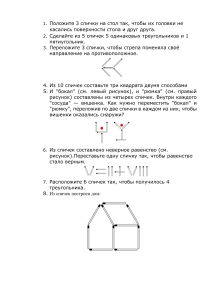
Фигура составлена из 10 спи­
чек. Переложите 2 спички так,
чтобы получилось 2 квадрата
разной величины.
Фигура составлена из 12 спи­
чек. Переложите 4 спички так,
чтобы получилось 2 квадрата
разной величины.
Фигура составлена из
16 спичек. Переложите
8 спичек так, чтобы полу­
чилось 3 квадрата.
21
\_ /
/ V
w
/ \
по
f___I
р
П-1
Фигура составлена
из 16 спичек. Перело­
жите 7 спичек так, что­
бы получилось 5 оди­
наковых квадратов.
Фигура составлеГ Ц “ Ц "|
на из 28 спичек. Пе- г- w
реложите 1 2 спичек
.=*#
так, чтобы получиU
LJ L
лось 9 квадратов.
Фигура составлена из
1 7 спичек.УберитеЗспички и переложите 4 спич­
ки так, чтобы получились
квадрат и прямоугольник.
20
22
Фигура составлена из
16 спичек. Переложите
4 спички так, чтобы полу­
чилось 8 квадратов одно­
го размера и 3 квадрата
другого.
спички
СП
Г -Р
I___ J
Фигура составлена
из 20 спичек. Пере­
ложите 4 спички так,
чтобы
получилось
8 квадратов одного
размера и 4 квадрата
другого размера.
Фигура составлена из
12 спичек. Переложите
б спичек так, чтобы полу­
чилось б квадратов.
22
Фигура составлена из 12 спи­
чек. Переложите б спичек так,
чтобы получилось 10 квадра­
тов.
23
Фигура составлена из 8 спи­
чек. Переложите 4 спички так,
чтобы получилось 14 квадра­
тов.
24
Из 16 спичек сложите 4 одинаковых
прямоугольника и 2 одинаковых квад­
рата.
25
23
\_ /
/ V
w
/ \
по
f___I
р
П-1
спички и ч и с л а
26
В фигуре, составленной из спи­
чек, переложите одну спичку так,
чтобы полученное число дели­
лось на 2.
В фигуре, составленной из спи- #'
чек, переложите одну спичку так,
чтобы полученное число дели­
лось на 3.
В фигуре,
составленной “ ЧГ
из спичек, переложите одну
спичку так, чтобы полученное
число делилось на 4.
29
24
В фигуре, составленной
из спичек,
переложите
одну спичку так, чтобы по­
лученное число делилось
на 5.
спички
CD r -fJ
I_ _ J
В фигуре, составленной
из спичек, переложите
одну спичку так, чтобы по­
лученное число делилось
на б.
В фигуре, составленной
из спичек, переложите
одну спичку так, чтобы по­
лученное число делилось
на 7.
В фигуре, составленной
из спичек, переложите
одну спичку так, чтобы по­
лученное число делилось
на 8.
В фигуре, составленной
из спичек, переложите
одну спичку так, чтобы по­
лученное число делилось
на 9.
30
31
32
33
25
\_ /
/ V
w
/ \
no
t_____)
_
р
П-1
спички и СЛОВА
34
В слове «шут», составленном из 15 спи­
чек, переставьте 2 и уберите 1 спичку
так, чтобы получилась мера длины, рав­
ная 12 дюймам.
35
В слове «честь», составленном из
21 спички, переставьте 1 и добавьте 3 спич­
ки так, чтобы получилась слово, означа­
ющее цифру.
26
спички
Щ
В слове «фетр», составленном из19спичек, переставьте 4 спички так, чтобы по­
лучилась единица измерения длины.
36
В слове «оборона», составленном
из 40 спичек, переставьте 2 и уберите
5 спичек так, чтобы получилось то, чего у
треугольника 3 , а у прямоугольника 4.
37
В слове «ступень», составленном из
32 спичек, переставьте 2 спички так, что­
бы получилось слово, стоящее в выраже­
нии «возведение в...».
38
27
\_ /
/ \_
\/
/л
1
и
&
I_____I
Д
\ Й 7
РИМСКИЕ ЧИСЛА
1
2
3
4
5
б
7
8
9
10
28
г
11
ос
12
не
13
IV
V
VI
VI
VII
IX
X
14
15
16
0
і
17
18
19
20
XI
XII
XIII
XIV
XV
XV!
XVI
XVII
XIX
XX
21
22
23
24
25
26
0
27
28
29
30
XXI
XXII
X X II
XXIV
XXV
XXVI
XXVII
XXVIII
XXIX
XXX
спички
го I
н
□
I
■
а р и ф м е т и ч е с к и е в ы р а ж ен и я
с рим ским и числам и
Уберите в выражении 1 спичку так,
чтобы получилось верное равенство.
Уберите в выражении 1 спичку так,
чтобы получилось верное равенство.
39
40
Переставьте в выражении 1 спичкутак,
чтобы получилось верное равенство.
Переставьте в выражении 1 спичкутак,
чтобы получилось верное равенство.
42
29
\_ /
/ V
w
/ \
43
44
45
46
30
по
f___I
р
П-1
Уберите в выражении 2 спички так,
чтобы получилось верное равенство.
Уберите в выражении 2 спички так,
чтобы получилось верное равенство.
Переставьте в выражении 2 спички так,
чтобы получилось верное равенство.
Переставьте в выражении 2 спички так,
чтобы получилось верное равенство.
спички
CD r -fJ
I_ _ J
Уберите в выражении 3 спички так,
чтобы получилось верное равенство.
Уберите в выражении 3 спички так,
чтобы получилось верное равенство.
47
48
Спички и р а в е н с т в а
Переставьте в выражении 2 спички так,
чтобы получилось верное равенство.
Уберите в выражении 1 спичку так,
чтобы получилось верное равенство.
49
50
31
\_ /
/ V
w
/ \
по
f___I
р
П-1
Переставьте в выражении 1 спичкутак,
чтобы получилось верное равенство.
52
Переставьте в выражении 2 спички так,
чтобы получилось верное равенство.
разны е з а д а ч и со с п и ч к а м и
53
32
Как из 12 спичек получить пять?
спички
CD r -fJ
I_ _ J
Как из 7 спичек получить восемнад­
цать, не ломая их?
Как из 5 спичек получить три?
Как из 9 спичек получить животное?
Как из 17 спичек получить время
года?
54
55
56
57
33
ес к и е квадраты
м а г и ч е с к и й к в ад ра т -
это та б л и ц а С
од инаковы м к о л и ч ес тв о м с т р о к и с тол б ц о в ,
в которой з а д а н н ы е ч и с л а р а с с т а в л ен ы т а к ,
чтобы и х с ум м ы в каж д о м с то л б ц е , в к а ж д о й
с т р о к е и д и а г о н а л я х бы ли равны .
ч.
н а тур ал ь н ы е ч и с л а - ч и с л а , которы м и
п о л ь з ую тс я п ри с ч ё т е , то е с т ь і , 2, 3 и т а к д а л е е .
п о с т р о е н и е м а г и ч е с к и х квад ратов
Прим ер 1
В квадрате 3x3 (три строки и три столб­
ца, говорят «три на три») расставьте на­
туральные числа от 8 до 16 так, чтобы
суммы чисел в каждой строке, каждом
столбце и диагоналях были равны. Опре­
делите эту сумму.
Реш ение.
1. НарисуемквадратЗхЗ.
34
МАГИЧЕСКИЕ КВАДРАТЫ
2. Добавим так называемые «террасы».
3.
Расставим натуральные числа от 8
до 16 по порядку в диагоналях так, как
показано на рисунке, последовательно
переходя на нижестоящуюдиагональ.
4.
Сдвинем закрашенные части внутрь
квадрата так, чтобы каждая часть сопри­
касалась с противоположной стороной
квадрата.
35
ч е с к и е квадраты
5. Получим результат.
Убедимся, что суммы чисел в каждой
строке, каждом столбце и диагоналях
равны.
Суммы чисел в строках:
11 + 16 + 9 = 36;
1 0 + 1 2 + 14 = 36;
15 + 8 + 13 = 36.
Суммы чисел в столбцах:
11 + 1 0 + 1 5 = 36;
16 + 12 + 8 = 36;
9 + 1 4 + 13 = 36.
Суммы чисел на диагоналях:
11 + 12 + 13 = 36;
9 + 1 2 + 15 = 36.
Суммы чисел в каждой строке, каждом
столбце и диагоналях равны 36.
36
м а г и ч е с к и е квадраты
Пример 2
В квадрате 5x5 расставьте натураль­
ные числа от 3 до 27 так, чтобы суммы
чисел в каждой строке, каждом столбце
и диагоналях были равны. Определите
эту сумму.
Решение.
1. Нарисуемквадрат5х5.
2. Нарисуем «террасы».
37
И
МАГИЧЕСКИЕ КВАДРАТЫ
3. РасставимчислаотЗдо27.
3
8
13
9
14
18
23
4
19
24
5
10
15
20
25
6
16
21
26
7
11
12
17
22
27
4. Сдвинем закрашенные части внутрь
квадрата так, чтобы каждая часть сопри­
касалась с противоположной стороной
квадрата.
5. Получим результат.
13 26
38
9
22
5
6
14 27 10 18
19
7
15 23 11
12 20
3
16 24
25
21
4
8
17
м а г и ч е с к и е квадраты
Убедимся, что суммы чисел в каждой
строке, каждом столбце и диагоналях
равны.
Суммы чисел в строках:
: 75;
6 + 144- 27 + 10 + 18 = 75;
19 + 7 + 15 + 2 3 + 1 1 = 75;
12 + 20 + 3 + 16 + 24 = 75;
25 + 8 + 21 + 4 + 17 = 75.
Суммы чисел в столбцах:
= 75;
26 + 14 + 7 + 20 + 8 = 75;
: 75;
22 + 10 + 23 + 16 + 4 = 75;
5 + 1 8 + 1 1 + 2 4 + 1 7 = 75.
39
И
м а г и ч е с к и е квадраты
Суммы чисел на диагоналях:
1 3 + 1 4 + 15 + 1 6 + 17 = 75;
5 + 10 + 15 + 20 + 25 = 75.
Суммы чисел в каждой строке, каждом
столбце и диагоналях равны 75.
м а г и ч е с к и е квад раты 3x 3, 5x 5, 7 x 7
В квадрате 3x3 расставьте
натуральные числа от 15 д о __________
23 так, чтобы суммы чисел
в каждой строке, каждом
столбце и диагоналях были ___ ___ ___
равны. Определите эту сум­
му.
59
40
В квадрате 5x5
расставьте натураль-__________________
ные числа от 10 до
34 так, чтобы суммы
чисел в каждой стро---------------ке, каждом столбце
и диагоналях были
равны. Определите --------------эту сумму.
м а г и ч е с к и е квадраты
В квадрате 7x7 расставьте натуральные
числа от 5 до 53 так, чтобы суммы чисел
в каждой строке, каждом столбце и диа­
гоналях были равны.
41
Щ
ГЕОМЕТРИЧЕСКИЕ ЗАДАЧИ
РАССТАНОВКА ФИГУР НА ДОСКЕ
Пример 3
Можно ли на квадратной до- I I I I I I
ске 6x6 расставить фигурки ц ц ц
і і і і і ітак, чтобы вся доска была I I I I I I
ими покрыта?
Решение.
Доска 6x6 состоит из 36 клеток, а фиг у р к а ^ ^ Ш состоит из 5 клеток. По­
крыть доску такими фигурками нельзя,
поскольку 36 неделится нацело на 5.
Пример 4
Расставьте на доске размером 8x8
фигурки^ ^ так, чтобы вся доска была
покрыта фигурками.
Решение.
Сначала определим, можно ли доску
покрыть такими фигурками. Количество
42
г е о м е т р и ч е с к и е зад
клеток на доске равно 64. В фигурке
4 клетки. Число 64 делится на 4 нацело.
Значит, доску 8x8 можно заполнить та­
кими фигурками. Попробуем:
Пример 5
На доске 6x12 клеток расставьте 8 фигурок^д и 10 ф и гур о к^ Р так, чтобы
вся доска была покрыта фигурками.
Решение.
L
ІГ ч
и
п
L
“L
_р
П
43
гео м етри ч ес к и е зад ачи
На доске 5x9 клеток рас­
ставьте 3 ф и г ур ки ^ и 6 фигурокЩ так, чтобы вся доска
была ими покрыта.
62
На доске 7x8 клеток расставь­
те 5 фигурок^^ и 12 фигурок
□0 так, чтобы вся доска была
ими покрыта.
63
На доске 6x9 клеток рас­
ставьте 8 ф и г у р о к ^ ^ и
11 фигурокш так, чтобы вся
доска ими была покрыта.
64
На доске 4x12 клеток
расставьте б фигурок J
3 фигурки^ А и 4 фигурк и ^ так, чтобы вся доска
была ими покрыта.
гео м етр и ч ес к и е ф игуры
65
Какую из фигур нельзя составить из
д в ухф и г ур о к в и д а ^ 7
1.
44
в
2.
3.
Ачи
гео м етри ч ес к и е
Какую из фигур нельзя составить из
двух фигурок вида
т
1.
3.
2.
4.
Какую из фигур нельзя составить из
двух фигурок в и д а щ ?
1.
67
3. £
2.
Какую из фигур нельзя составить из
двух фигурок в и д а ^ ^ ?
//
1. /~
-о 2
3. £
.
4.
Какую из фигур нельзя составить из
двух фигурок вида^ ^ 7
1.
///
/
У~л 2 .
V
3.
/////
/
~
4.
/
45
ГЕОМЕТРИЧЕСКИЕ ЗАДАЧИ
70
Какую из фигур нельзя составить из
двух фигурок вида^й^ ?
1.
71
Й Ьз.
2.
£
£
Какую из фигур нельзя составить из
д в ухф и г ур о кв и д а ^ ^ 7
1.
а
4.
КОЛИЧЕСТВО КУБИКОВ в ФИГУРЕ
Сколько кубиков использо­
вали для построения фигуры,
изображённой на рисунке?
^
Сколько кубиков использо­
вали для построения фигуры,
изображённой на рисунке?
^
Сколько кубиков использо­
вали для построения фигуры,
изображённой на рисунке?
46
И
гео м етри ч ес к и е
Ачи
Сколько кубиков использо­
вали для построения фигуры,
изображённой на рисунке?
75
Пример 6
На рисунке изображён робот. Сколько
здесь квадратов?
47
гео м етри ч ес к и е зад ачи
Решение.
Считаем количество квадратов:
- 1 квадрат;
і і і і і і і L-LLi - 10 квадратов;
Щ
- 4 квадрата 1х1;1квадрат 2x2;
— 16 квадратов 1x1; 9 квадратов
2x2; 4 квадрата 3x3; 1 квадрат 4x4;
— 2 квадрата.
Привет!
Общее количество квадратов:
1 + 10 + 4 + 1 + 16 + 9 + 4 + 1 + 2 =
= 48.
з а д а ч и с к уб и к а м и
р а з в ё р т к а и гр а л ь н о го к у б и к а -
это ш аб л о н
к у б и к а , к о то ры й м о ж н о п о л у ч и т ь , Если
р а з р е з а т ь к у б и к вдоль н е к о т о р ы х е г о р ё б е р
г р а н ь и гр а л ь н о го к у б и к а - о д н а с т о р о н а
^
48
к уб и к а , на которой н а р и с о в ан ы т о ч к и .
гео м етри ч ес к и е
р е б р о и гр а л ь н о го к у б и к а -
это линия, вдоль
КОТОРОЙ СОЕДИНЯЮТСЯ ДВЕ СОСЕДНИЕ
ГРАНИ КУБИКА.
НА КАЖДОЙ ГРАНИ КУБИКА НАРИСОВАНЫ ТОЧКИ:
НА ОДНОЙ - ОДНА ТОЧКА, НА ДРУГОЙ - ДВЕ ТОЧКИ,
НА ТРЕТЬЕЙ - ТРИ ТОЧКИ. ГРАНЕЙ У КУБИКА 6,
ЗНАЧИТ, МАКСИМАЛЬНО НА ГРАНИ МОЖЕТ БЫТЬ
ШЕСТЬ ТОЧЕК.
На рисунке изображены игральный ку­
бик и его развёртка. Сколько точек нахо­
дится на нижней грани и боковой грани
слева?
На рисунке изображены игральный ку­
бик и развёртка. Сколько точек находит­
ся на боковой грани слева и на боковой
грани справа?
49
гео м етри ч ес к и е зад ачи
78
79
Среди приведённых кубиков найдите
одинаковые.
1. |< Е > | 2 .
4.
3.
На рисунке изображены два одинако­
вых игральных кубика. Сколько точек на­
ходится на нижних гранях кубиков?
іО
а
і< £ ? і
с о с т а в л е н и е кв ад ратов и прям оугольников
Составьте прямоугольник 5хб клеток
из следующих фигур:
[
□
Т2 СП
в
Составьте прямоугольник 6x8 клеток
50
гео м етри ч ес к и е
Ачи
из следующих фигур:
Составьте квадрат 6x6 клеток
из следующих фигур:
Составьте прямоугольник 4x8 клеток
из следующих фигур:
51
ГЕОМЕТРИЧЕСКИЕ ЗАДАЧИ
84
Составьте квадрат 8x8 клеток
из следующих фигур:
[
[
С
РАЗРЕЗАНИЕ ФИГУР
85
Разрежьте прямоугольник 0,5x5 см на
прямоугольники по сторонам клеток так,
чтобы сумма их периметров была рав­
на 14 см. Стороны одной клетки равны
0,5 см.
Разрежьте прямоугольник 1x2 см на
прямоугольники по сторонам клеток
так, чтобы сумма их периметров была
равна 11 см. Стороны одной клетки
равны 0,5 см.
52
гео м етри ч ес к и е
Ачи
Разрежьте квадрат 2x2 см на прямо­
угольники по сторонам клеток так, чтобы
сумма их периметров была равна 16 см.
Стороны одной клетки равны 0,5 см.
87
Разрежьте прямоугольник 1x5 см на
прямоугольники по сторонам клеток
так, чтобы сумма их периметров была
равна 24 см. Стороны одной клетки
равны 0,5 см.
Разрежьте прямоугольник 2x4 см на
прямоугольники по сторонам клеток
так, чтобы сумма их периметров была
равна 28 см. Стороны одной клетки
равны 0,5 см.
53
гео м етри ч ес к и е зад ачи
расстановка ч и с ел
В прямоугольнике 4x9 клеток рас­
ставьте натуральные числа так, чтобы
при любом расположении фигурки вида
j=ppj сумма чисел в её семи клетках была
равна 21, а в каждой фигурке вида №
сумма чисел была равна 12.
Можно ли в квадрате 5x5 клеток рас­
ставить натуральные числа так, чтобы
при любом расположении фигурки вида
^ сумма чисел в её пяти клетках была
равна 9 или 21, а в каждой фигурке вида
ш сумма чисел была равна б?
92
54
В квадрате 6x6 клеток расставьте на­
туральные числа так, чтобы при любом
расположении фигурки в и д а ^ сум­
ГЕОМЕТРИЧЕСКИЕ ЗАД
ма чисел в трёх её клетках была равна
12 или 18, а в каждой фигурке вида
сумма чисел в четырёх её клетках была
равна 20.
Можно ли в прямоугольнике 6x8 кле­
ток расставить натуральные числа так,
чтобы при любом расположении фи­
гурки ви д а^ т Л сумма чисел в её ше­
сти клетках была равна 28, а при любом
расположении фигурки в и д а ^ сумма
чисел была равна 17?
Можно ли в прямоугольнике 4x12 кле­
ток расставить натуральные числа так,
чтобы при любом расположении фигур­
ки в и д а Ш ^ сумма чисел в её четырёх
55
гео м етри ч ес к и е зад ачи
клетках была равна 18, а в каждой фи­
гурке в и д а Ш ^ сумма чисел в трёх её
клетках была равна 11?
д е л е н и е ф и г у р ы н а равны е ч а с т и
95
И
56
Найдите пять способов разрезания
прямоугольника 2x10 клеток на две рав­
ные части так, чтобы линия разреза шла
по сторонам клеток.
Найдите восемь способов разрезания
прямоугольника 6x8 клеток на две рав­
ные части так, чтобы линия разреза шла
по сторонам клеток.
гео м етри ч ес ки е
Ачи
Можно ли прямоугольник 7x5 клеток
разрезать на две равные части так, чтобы
линия разреза шла по сторонам клеток?
Если можно, приведите пример, если
нельзя, объясните почему.
97
Разделите фигуру, изображённую на
рисунке, на две равные части так, чтобы
линия разреза шла по сторонам клеток.
Разделите
фигуру,
изображённую
на рисунке, на пять равных частей так,
чтобы линия разреза шла по сторонам
клеток.
57
Щ
гео м етри ч ес к и е зад ачи
п о д с ч е т прям оугольников , треуго л ь н и к о в
и кв ад ратов
100
Сколько прямоугольников изображено
на рисунке?
1 . 18 .
101
Сколько
рисунке?
1. 2 8 .
102
3. 20.
квадратов
2. 29.
Сколько
рисунке?
1. 4 8 .
58
2 . 19 .
3. 30.
квадратов
2. 4 9 .
3. 50.
4. 21.
изображено
на
4. 31.
изображено
4. 51.
на
ГЕОМЕТРИЧЕСКИЕ
АЧИ
Сколько треугольников изображено на
рисунке?
1. 14.
2. 15. 3. 16.
103
4. 17.
59
п р и з н а к и д ел и м о с т и
• Число делится на 2, если оно оканчи­
вается на 0, 2, 4, 6, 8 (46, 78, 120).
• Число делится на 3, если сумма цифр
числа делится на 3 (345 делится на 3, так
как сумма цифр числа 3 + 4 + 5 = 12
делится наЗ).
• Число делится на 4, если число, об­
разованное последними двумя цифрами
данного числа, делится на 4 (348 делится
на 4, так как 48 делится на 4; 12 380 делит­
ся на 4, так как 80 делится на 4).
• Число делится на 5, если оканчивает­
ся на 5 или на 0 (850 делится на 5, так как
оканчивается на 0; 765 делится на 5, так
какоканчивается на5).
• Число делится на б, если делится на
2 и на 3, то есть оканчивается на 0, 2, 4, 6,
8 и сумма цифр числа делится на 3 (9576
делится на 2, так как оканчивается на б и
делится на 3, так как 9 + 5 + 7 + 6 = 27
делится наЗ).
• Число делится на 8, если число, обра­
зованное последними тремя цифрами дан-
60
ного числа, делится на 8 (456 328 делится
на 8, так как 328 делится на 8; 87 440 де­
лится на 8, так как 440 делится на 8).
• Число делится на 9, если сумма цифр
числа делится на 9 (4329 делится на 9, так
как сумма цифр числа 4 + 3 + 2 + 9 =
= 18 делится на 9).
• Число делится на 10, если оно окан­
чивается на 0 (1180 делится на 10, так как
оканчивается на 0).
• Число делится на 11, если сумма цифр
этого числа, стоящих на чётных местах, даёт
такой же остаток при делении на 11, как
сумма цифр, стоящих на нечётных местах
(23 496 делится нацело на 11, так как сум­
ма цифр, стоящих на нечётных местах 2 +
+ 4 + б = 12 при делении на 11 даёттакой
же остаток 1, как и сумма цифр, стоящих на
чётныхместахЗ + 9 = 12).
• Число делится на 25, если оканчивает­
ся на 00, 25, 50, 75 (525, 700, 875, 150).
• Число делится на 100, если оканчива­
ется двумя нулями (800, 1200, 2300).
61
с о с тав л ен и е ч и с ел
Прим ер 7
Никита и Максим играют в игру. Маль­
чики составляют различныечисла, стира­
ют в них некоторые цифры и предлагают
сопернику определить задуманное чис­
ло с помощью подсказок. Никита приду­
мал число, записал его и стёр несколько
цифр. С помощью подсказок определите
число, придуманное Никитой.
П од сказки .
1. Число шестизначное.
2. Числоделитсяна25.
3. Всецифрычисларазличны.
Реш ение.
1.
Число шестизначное, значит, нужно
найти две недостающие цифры.
62
Р Ч П Ю Я 1
2. Число делится на 25, если оканчи­
вается на 00, 25, 50, 75.
3. В то же время число составлено из
различных цифр, а это значит варианты
00, 25, 75 не подходят, так как в этом
случае в задуманном числе имеются по­
вторяющиеся цифры.
4. Подходит один вариант, когда чис­
ло оканчивается на 50, в этом случае вы­
полняются все условия-подсказки.
Полученное число:
Составьте двухзначное число, деляще­
еся н а 1 2 и н а 1 5 ?
104
Составьте наименьшее натуральное
число, которое делится на 2, 3, 5, 6, 9,
10, 15.
105
Составьте трёхзначное число, которое
делится на 2, 3 ,5 ,9 ,1 1 .
106
63
ДЕЛИМОСТЬ
107
Составьте наибольшее натуральное
число, оканчивающееся на 74, все циф­
ры которого различны.
108
Составьте наименьшее шестизнач­
ное натуральное число, делящееся на 9,
цифры которого различны.
109
Составьте наибольшее семизначное
натуральное число, которое делится
на 8.
110
Составьте наименьшее восьмизнач­
ное натуральное число, которое делится
на 45.
Составьте наименьшее пятизначное
натуральное число, состоящее из раз­
личных цифр, делящееся на б.
Составьте трёхзначное натуральное
число, которое оканчивается на 8, де­
лится на 72, все цифры различны.
113
Составьте трёхзначное число, которое
делится на 3 и 11, оканчивается на 9, а
сумма цифр равна 21.
114
Маша, Саша, Ваня и Дима участвуют
в игре «Найди клад». Ребята нашли сун­
64
Р Ч П Ю Я 1
ЯЕК2
ШШШШ
дук, и теперь им нужно определить не­
достающие цифры кода, чтобы его от­
крыть.
Частично известен код и даны подсказ­
ки.
7 4 1 5 * 0 3 *
2. Числоделитсяна8.
3. Сумма всех цифр равна 28.
Полина придумала пароль,
115
65
а спустя какое-то время забыла две циф­
ры, но помнила, что придуманное число
делится на 15 и 18. Определите пароль,
который придумала Полина.
6 ...8 Д 4 7 6 4
66
РАВЕНСТВА, КАРТОЧКИ, РЕБУСЫ
ЗНАКИ АРИФМЕТИЧЕСКИХ ДЕЙСТВИЙ
Пример 8
Имеется пять пятёрок. Расставьте меж­
ду некоторыми (или всеми) пятёрка­
ми знаки арифметических действий и
скобки так, чтобы получились числа от О
до 10.
Решение.
'і
t r t
1
I
г
Li
(5+ 5-5 -5):5=С>
55: S —СГ_ <Г= -I
( 5 + 5 ): 5 + 5 - 5 =2
(5• 5 - 5 -5):5 = 3
/ Г і Г і C l r-\. Г - Л
5-5+5--5+5 =5"
55:55+і Г=<э
5:5+5:5+5~ 7
(5+ 5+ 5): 5+ 5 = 8
С5-5-&\:5+5 = 9
[5-5+5- 5): s= 3-С
67
РАВЕНСТВА, КАРТОЧКИ, РЕБУСЫ
116
Даны пять семёрок. Расставьте между
некоторыми из них знаки арифметиче­
ских действий и скобки так, чтобы зна­
чение выражения стало равно 5.
7 7 7 7 7=5
117
Даны пять пятёрок. Расставьте между
ними знаки арифметических действий
так, чтобы значение выражения стало
равно 100.
5 5 5 5 5-г00
118
Даны семь троек. Расставьте между не­
которыми тройками знаки арифметиче­
ских действий так, чтобы значение вы­
ражения стало равно 10.
3 3 3 3 3 3 Ъ-ИО
68
р а в е н с т в а , к а р т о ч к и , р еб ус ы
Расставьте между 1, 2, 3, 4, 5, 6, 7, 8
знаки арифметических действий так,
чтобы значение выражения стало рав­
но 11.
119
Даны десять восьмёрок. Расставьте
между некоторыми из них знаки умно­
жения и сложения так, чтобы значение
выражения стало равно 200.
120
8 8 8 8 8 8 8 8 8
2 2-00
-
Даны семь двоек. Расставьте между не­
которыми из них знаки арифметических
действий так, чтобы значение выраже­
ния стало равно 100.
121
я я я я я я х-гоо
69
р а в ен с т в а , к а р то ч к и , реб ус ы
122
Расставьте между восемью десятками
знаки арифметических действий и скоб­
ки так, чтобы значение выражения стало
равно 5.
го го го го го го го го-s
123
Между семью четвёрками расставь­
те знаки арифметических действий так,
чтобы значение выражения стало равно21.
4 4 4 4 4 4 4 —2-It-
124
Между числами 3, 5, 8, 3, 5, 8, 3 рас­
ставьте знаки арифметических действий
и скобки так, чтобы значение выражения
стало равно 5.
3 5 8 3 5 8 3=5
70
р а в е н с т в а , к а р т о ч к и , р еб ус ы
В заданном выражении расставьте
скобки так, чтобы получилось верное
равенство.
125
б а -П Я + З + Д 2 4 = 5 * 2
ч и с л а на к а р т о ч к а х
Вася составляет верные равенства
из карточек, на каждой из которых на­
писана цифра, знаки арифметических
действий или скобки, а затем несколько
карточек переворачивает. Определите,
что написано на перевёрнутых карточках
(1 2 6 -1 3 0 ).
! □Ш1Ѳ @ ВI □1В И
ВПВПВВ0В0ВВІ
ВВПВВВВПИВВИ
126
127
128
71
р а в ен с т в а , к а р то ч к и , реб ус ы
129
130
00B@D00iOD@0
0 і 1 □0 0й Ѳ HIи □і
ч и с л о в ы е и б укв ен н ы е РЕБУСЫ
Прим ер 9
Замените фигурки цифрами так, что­
бы получилось верное равенство. Оди­
наковые фигурки означают одинаковые
цифры.
Реш ение.
Наибольшая сумма при сложении
двух цифр равна 18 (9 + 9). В старший
разряд переходит 1. Сумма двух девяток
и единицы, которая переходит из млад­
шего разряда, равна 19. И в этом случае
в старший разряд опять переходит еди­
ница. Видим, что в старший разряд при
72
р а в е н с т в а , к а р т о ч к и , р еб ус ы
сложении двух цифр может переходить
только единица. Очевидно, что на месте
фигуркип в разряде тысяч стоит циф­
ра 1, значит, в разряде единиц на месте
фигурокптакже стоят 1.
1 ▲• ♦
Получается, на месте фигуркиО в раз­
ряде единиц стоит 2, значит, и в разряде
сотен стоят 2.
Видим, что на месте А в разряде сотен
стоит 4.
Складывая какие числа, можно полу­
чить то же самое число? Складывая нули.
73
р а в ен с т в а , к а р то ч к и , реб ус ы
Значит, в разряде десятков вместо фигурокО стоят 0.
В числовых ребусах вместо звёздочек
поставьте цифры так, чтобы получилось
верное равенство (1 3 1 -1 3 4 ).
1131
а )+ 2 3 *
* 9 5
б)
*
9
*
2 * 6 5
1132
* 8 * 9
4 9 5
133
х
74
б)
1
1 * 8
* 0
9 2 *
б)
9 * * 1
* 7 8 *
7 7
х
8
5 * 0
р а в е н с т в а , к а р т о ч к и , РЕБУСЫ
3* 5*
3 4 *
2 * *
* * 5
“О
б)
* * 6 8
7 *
* 5 *
"| * *
*
134
g *
О
Замените фигурки или буквы цифрами
так, чтобы получилось верное равенство.
Одинаковые фигурки и буквы означают
одинаковые цифры.
135
7 5
з а к о н о м ер н о с ти
ч и с л а п о с л ед о в а тел ь н о с ти
Пример 10
Запишите следующие три числа после­
довательности:
1 ,3 ,6 , 1 0 ,1 5 ,2 1 ..............
Решение.
Сначала определим, как получилась
такая последовательность:
1 + 2 = 3;
3 + 3 = 6;
6 + 4= 10;
10 + 5 = 15;
15 + 6 = 21.
Следующие числа:
2 1 + 7 = 28;
28 + 8 = 36;
36 + 9 = 45.
Ответ: 28; 36; 45.
136
Запишите следующие три числа после­
довательности:
33, 303, 3003, ..., ..., ...
76
9 \
___
Запишите следующие три числа после­
довательности:
137
9, 18, 36, 72, 144, ..., ..., ...
Запишите следующие три числа после­
довательности:
138
6 .1 1 .9 , 1 4 ,1 2 ,1 7 ..............
Запишите следующие три числа после­
довательности:
139
3 ,1 2 ,6 ,2 4 ,1 2 ,4 8 , 24..............
Запишите следующие три числа после­
довательности:
140
169, 144, 121, 100, ..., ..., ...
Запишите следующие два числа по­
следовательности:
141
2,5, 14,41,12 2.........
Запишите следующие два числа по­
следовательности:
142
4, 12, 36, 108, ..., ...
Запишите следующие три числа после­
довательности:
143
4 .5 .9 ,.1 8 ,3 6 ,7 2 ..............
77
з а к о н о м ер н о с ти
1ЧЧ
Запишите следующие три числа после­
довательности:
2 ,7 ,1 5 ,2 6 ,4 0 ..............
145
Запишите следующие три числа после­
довательности:
1 ,8 ,2 , 7, 6, 4, ..., ..., ...
146
Запишите следующие три числа после­
довательности:
98, 97, 94, 89, 82, ..., ..., ...
147
Запишите следующие три числа после­
довательности:
1 ,4 ,1 2 ,1 5 ,4 5 ,4 8 ..............
148
Запишите следующие два числа по­
следовательности:
1,16, 81,625,..., ...
149
Запишите следующие три числа после­
довательности:
3 ,4 ,7 ,1 1 , 18,29..............
150
Запишите следующие три числа после­
довательности:
7, 15, 24, 34, 45, 57, ..., ..., ...
78
К
6
I 1 16 5
14
ч
4
3
/
/
ЗАКОНОМЕРНОСТ
20
4П И 6
15
9
10
Запишите следующие три числа после­
довательности:
151
5, 6, 7, 18, 31, 56, ..., ..., ...
Запишите следующие три числа после­
довательности:
152
5, 15,35,65, 105, ..., ..., ...
Запишите следующие три числа после­
довательности:
153
1 4 ,1 5 ,1 3 ,1 6 ,1 2 ,1 7 ,1 1 ,1 8 ,1 0 ,1 9 ,
ЗАКОНОМЕРНОСТИ В ЧИСЛОВЫХ РЕБУСАХ
Прим ер 11
Определите число, стоящее вместо во­
просительного знака.
Ре ш е н и е .
Попытаемся выяснить, какая зависи­
мость существует между числами:
15 + 47 = 62;
37 + 1 5 = 52.
Ответ: 52.
79
з а к о н о м ер н о с ти
В числовых ребусах определите число,
стоящее вместо вопросительного знака
(1 5 4 -1 5 6 ).
154
155
156
Пример 12
Какие цифры стоят вместо вопроси­
тельных знаков?
Решение.
17834 + 31 155 = 48989.
Ответ: 1;8.
80
Какая цифра стоит на месте вопроси­
тельного знака?
157
Пример 13
Запишите числа, стоящие вместо во­
просительных знаков.
Решение.
Выясним, как числа связаны друг с
другом:
2 1 + 7 = 28;
28 + 7 = 35;
35 + 7 = 42;
42 + 7 = 49;
49 + 7 = 56.
Ответ: 5; 6.
81
з а к о н о м ер н о с ти
В числовых ребусах определите число,
стоящее вместо вопросительного знака
(1 5 8 -1 7 1 ).
158
159
160
7~|| 15 III 31 іГ б З ІГ ?
3
162
163
82
10
11 ЕЖ
Т|д[9І0][2І2][223]
17
|313||233||343
з ак о н о м ерн о с т
164
165
166
167
168
83
рности
170
172
Костя составил последовательность из
пяти чисел. Затем одно число заменил
знаком вопроса и предложил опреде­
лить его Пете. Петя предположил, что это
число 47. Прав ли Петя?
14
84
22
30
38
ч ётн о с ть
Ооооо
ооооо
ооооо
ооооо
ооооо
ч е т н ы е и н еч ёт н ы е ч и с л а
чётны м чи с л о м назы ваю т ЦЕЛОЕ ч и с л о ,
д ел я щ еес я н а 2 БЕЗ остатка
(2 : 2 = 1; 4 : 2 = 2; 6 : 2 = 3).
нечётны м ч и с л о м назы ваю т ц ел о е ч и с л о ,
которое п ри д ел ен и и н а 2 д а ёт остаток 1
(3, 5, 79, ...).
сложение чётных и нечётных чисел
ЧЁТНОЕ + ЧЁТНОЕ = ЧЁТНОЕ ЧИСЛО
ЧЁТНОЕ + НЕЧЁТНОЕ = НЕЧЁТНОЕ ЧИСЛО
НЕЧЁТНОЕ + ЧЁТНОЕ = НЕЧЁТНОЕ ЧИСЛО
НЕЧЁТНОЕ + НЕЧЁТНОЕ = ЧЁТНОЕ ЧИСЛО
в ы ч и тан и е ч ёт н ы х и н еч ётн ы х ч и с ел
ЧЁТНОЕ - ЧЁТНОЕ = ЧЁТНОЕ ЧИСЛО
ЧЁТНОЕ - НЕЧЁТНОЕ = НЕЧЁТНОЕ ЧИСЛО
НЕЧЁТНОЕ - ЧЁТНОЕ = НЕЧЁТНОЕ ЧИСЛО
НЕЧЁТНОЕ - НЕЧЁТНОЕ = ЧЁТНОЕ ЧИСЛО
ум н о ж ен и е ч ё т н ы х и н еч ётн ы х ч и с ел
ч ётн о е • ч ётн о е = ч ётн о е число
ч ё т н о е • НЕЧЁТНОЕ = ЧЁТНОЕ ч и с л о
НЕЧЁТНОЕ • ЧЁТНОЕ = ЧЁТНОЕ ЧИСЛО
НЕЧЁТНОЕ • НЕЧЁТНОЕ = НЕЧЁТНОЕ ЧИСЛО
85
Чётность
м о ж е т - н е м о ж ет
Пример 14
Можно ли разменять 45 рублей при
помощи 16 монет достоинством в 1, 3,
5, 7 рублей? Если да, напишите как.
Решение.
Нет, нельзя. В данной задаче представ­
лены монеты в 1, 3, 5, 7 рублей — числа
нечётные. 45 рублей нужно разменять
шестнадцатью монетами. Сумма шест­
надцати нечётных чисел является числом
чётным, а 45 рублей — число нечётное,
значит, выполнить предложенный раз­
мен невозможно.
Пример 15
Катя пригласила несколько девочек на
свой день рождения. Каждая девочка на
празднике съела столько конфет, сколь­
ко исполнилось лет Кате. Могло ли так
86
Чётность
ооооо
ооооо
ооооо
ооооо
ооооо
получиться, что всего было съедено не­
чётное число конфет, если Кате исполни­
лось 8 лет?
Решение.
Каждая девочка на празднике съела
8 конфет (число чётное), так как Кате
исполнилось 8 лет. Сумма чётных чисел
(независимо от количества) является
чётным числом, значит, такого быть не
могло.
Коля купил б игрушек, каждая из ко­
торых стоила 45, 65 или 77 рублей. Мог
ли он заплатить 383 рубля?
Оля, Катя, Ира и Лиза вырезают сне­
жинки. Каждая девочка вырезала нечёт­
ное число снежинок от 10 до 20 штук.
Могло ли получиться так, что всего де­
вочки вырезали 65 снежинок?
173
174
87
ч ёт н о с т ь
175
176
177
Люба, Ира и Полина собирают цветы.
Каждая девочка собрала букет из нечёт­
ного числа цветов. Могло ли получиться
так, что всего девочки собрали 100 цве­
тов?
Костя придумал три натуральных не­
чётных числа и сложил их. Получилось
120. Подумайте, не ошибся ли Костя, а
если ошибся, объясните почему.
Без вычислений определите чётной
или нечётной является сумма всех на­
туральных чисел от 101 до 200? Затем
найдите эту сумму.
Пример 16
Даша и Гоша написали на карточках
числа от 5 до 15, затем их перемешали.
Даша взяла себе пять карточек, а Гоша
три, оставшиеся карточки отложили.
Даша, посмотрев свои карточки, сказа­
ла Гоше: «Сумма чисел, написанных на
твоих карточках, нечётная». Какие числа
написаны на карточках Гоши? Возможны
ли другие варианты?
88
Чётность
ооооо
ооооо
ооооо
ооооо
ооооо
Решение.
Карточки можно разделить на две
группы: с чётными числами и с нечёт­
ными числами. Всего 5 чётных чисел
и б нечётных.
Если у Даши все 5 карточек с чётными
числами, то у Гоши могут быть карточ­
ки только с нечётными числами, а сум­
ма любых трёх нечётных чисел является
нечётным числом, о чём Даша и сказала
Гоше.
Если же Даше попались или все нечёт­
ные, или и чётные, и нечётные числа, то
неясно, сколько чётных и нечётных чи­
сел попалось Гоше, а значит, нельзя сде­
лать вывод о том, чётна или нечётна их
сумма.
Полина, Кристина и Юля написали на
карточках по четыре числа. Полина на­
писала 54, 23, 5, 12, Кристина написала
18, 76, 15, 1, а Юля - 65, 43, 2, 8. За­
тем каждая девочка отдала своим под­
ругам по две карточки. У Полины сумма
каких-то двух полученных карточек со­
178
89
Чётность
ставила 91. У Юли сумма чисел на кар­
точках оказалась нечётной. Какие числа
написаны на карточках, которые получи­
ла Юля, если их сумма меньше 50?
Полина
Кристина
Юля
179
90
В магазине работают 23 продавца,
причём в смене работает 5 человек. М о­
жет ли так оказаться, что через какое-то
время каждый продавец с остальными
работал ровно один раз?
ооооо
ооооо
ооооо
ооооо
ооооо
Чётность
Пример 17
Может ли конь, стоящий на клетке В8,
через 8 ходов оказаться на клетке А8?
8
t
7
6
5
4
3
2
1
А
в
с
D
Е F
G н
Решение.
Делая один ход, конь встаёт на клетку
другого цвета. Делая ещё шаг, конь вста­
ёт на клетку, цвет которой совпадает с
цветом клетки, на которой стоял перво-
91
ч ёт н о с т ь
начально. При чётном количестве ходов
конь встаёт на клетку, цвет которой со­
впадает с цветом первоначальной клет­
ки. При нечётном количествеходов конь
встаёт на клетку, цвет которой не совпа­
даете цветом первоначальной клетки.
Клетка В8 —чёрная, значит, через 8 хо­
дов конь должен встать также на чёрную
клетку. Клетка А8 белая, поэтому такого
быть не может.
180
Может ли конь, стоящий на клетке D1,
через 25 ходов оказаться на клетке F1?
Пример 18
Вове в домашнем задании попалась
следующая задача: «Определите чётным
или нечётным является произведение
(11х - 1 2 у + 5 ) • (5х + 1 8 у - 2),
где х , у — натуральные числа».
Помогите Вове решить задачу.
Решение.
Сложим множители данного выраже­
ния:
1 1 х - 1 2 у + 5 + 5х + 1 8 у - 2 =
— 16х + 6у + 3.
92
Чётность
ооооо
ооооо
ооооо
ооооо
ооооо
Слагаемые 16х и 6у являются чётны­
ми, а число 3 — нечётное, значит, вы­
ражение 16х + бу + 3 является не­
чётным. Поскольку сумма множителей
11 х - 12 у + 5 и 5х + 18у - 2 за­
данного выражения является нечётным
числом, значит, одно из слагаемых 11 х - 12у + 5 и 5х + 18у - 2 чётно, другое
нечётно. Следовательно, произведение
является чётным числом.
Полине на математической олимпиаде
попалась задача: «Определите чётным
или нечётным является выражение
181
(15х + 24у + 5) •(17х + 18у + 4) + 7,
где х, у — натуральные числа».
У Полины получилось чётное число.
Права ли Полина?
На доске 5x5 стоят 25 фишек, по одной
в каждой клетке. Миша передвинул все
фишки так, что каждая фишка оказалась
на соседней по стороне клетке, причём
несколько фишек могут оказаться на
182
93
Чётность
одной клетке. Докажите, что какая-то
клетка останется пустой.
183
Записаны четыре числа: 7, 8, 9, 11.
За один ход разрешается прибавить 3 к
любым двум из этих чисел. Можно ли за
несколько ходов получить четыре оди­
наковых числа?
184
Костя в ряд выписал натуральные чис­
ла от 15 до 24. Можно ли расставить
между числами «+» и «-» так, чтобы по­
лучилось 2.
185
За круглым столом сидят 12 детей, ко­
торые решают примеры, причём количе­
ство решённых примеров у детей, сидя­
94
Чётность
ооооо
ооооо
ооооо
ооооо
ооооо
щих по соседству, отличается на 1. Могли
ли дети в сумме решить 77 примеров?
У Саши есть 54 кубика. Может ли Саша
в ряд составить из кубиков пять башен
так, чтобы количество кубиков, из ко­
торых составлены соседние башни, от­
личалось бы на чётное число кубиков,
причём первая башня составлена из трёх
кубиков?
186
95
Щ І
РАЗНЫЕ здддчи
ЗАД/МАННОЕ ЧИСЛО
П р и м ер 19
Миша задумал число. Прибавил к чис­
лу 4, затем умножил на 5, вычел 19 и по­
делил на 3. Получилось 17. Определите
задуманное число.
Реш ение.
Решим задачу по действиям, но в об­
ратном порядке, то есть заменим дей­
ствия обратными (деление — умноже­
нием, сложение — вычитанием и так
далее):
1 7 - 3 = 51;
5 1 + 1 9 = 70;
7 0 : 5 = 14;
14-4=
10.
Ответ: 10.
187
96
Катя задумала число. Отняла от числа
23, поделила на 4, вычла 31 и умножила
на б. Получилось 18. Определите число,
которое задумала Катя.
РАЗНЫЕ ЗАДАЧИ t. «
Ира задумала число. Прибавила к чис­
лу 15, поделила на 11, вычла 1, умно­
жила на 17, прибавила к полученному
числу 40. Получилось 74. Определите
число, которое задумала Ира.
Никита задумал число. Прибавил к
числу 50, умножил на 2, вычел 45, по­
делил на 3, прибавил 41, поделил на 2.
Получилось 38. Определите число, кото­
рое задумал Никита.
188
189
НАИБОЛЬШЕЕ И НАИМЕНЬШЕЕ ЧИСЛА
В заданном числе зачеркните две циф­
ры так, чтобы получилось наибольшее
число.
190
10Я52 4
В заданном числе зачеркните три циф­
ры так, чтобы получилось наименьшее
число.
31420S4Z
97
Щ І
РАЗНЫЕ ЗАДАЧИ
192
В заданном числе зачеркните три циф­
ры так, чтобы получилось наибольшее
число.
Ь
<Я
Ъ
Ъ
0
193
05
5
В заданном числе зачеркните четыре
цифры так, чтобы получилось наимень­
шее число.
<bZ24057322
ВЫПАВШИЕ СТРАНИЦЫ
П р и м е р 20
У Саши из книги выпало несколько
страниц, первая из которых имеет номер
365. Номер последней страницы запи­
сывается теми же цифрами, но в другом
порядке. Определите номер последней
страницы и количество выпавших ли­
стов.
Реш ение.
Если первая страница начинается с не­
чётного числа, то последняя страница бу-
98
разны е з а д а ч и
«. I *5 Щ Ш
дет чётной. Поскольку в числе 365 толь­
ко одна чётная цифра, номер последней
страницы оканчивается на б. Получает­
ся два варианта — 356 или 536, но но­
мер последней страницы не может быть
меньше первой. Номер последней стра­
ницы — 536.
Количество выпавшихлистов:
(536 - 365 + 1) : 2 = 86.
Мы разделили на 2, так как на одном
листе две страницы.
У Маши из книги выпало несколько
страниц. Номер первой страницы 683.
Номер последней страницы записывает­
ся теми же цифрами, но в другом поряд­
ке. Определите номер последней стра­
ницы.
У Полины из книги выпало 10 страниц.
Сумма номеров всех выпавших страниц
275. Определите номер первой и по­
следней страниц, выпавших из книги.
194
195
99
щ і
разны е з а д а ч и
к о ш к и -м ы ш ки
Пример 21
Мышке до норки 27 шагов. Кошке до
мышки 5 прыжков. За один прыжок кош­
ки мышка делает 4 шага. Один прыжок
кошки равен 12 шагам мышки. Догонит
ли кошка мышку, или мышка успеетспрятаться в норке?
Решение.
Один прыжок кошки равен 12 ша­
гам мышки. Пока кошка делает прыжок,
мышка делает4 шага. Получается каждый
раз расстояние между кошкой и мышкой
уменьшается на 8 шагов. Запишем рас­
стояния в шагах мышки. Сначала рассто­
яние от кошки до мышки 5 прыжков, то
есть 60 шагов мышки. Запишем:
100
РАЗНЫЕ ЗАДАЧИ і. §
Расстояние
от кошки
до мышки
Расстояние
от мышки
до норки
Сначала
60
27
1-й прыжок
кошки
52
23
2-й прыжок
кошки
44
19
3-й прыжок
кошки
36
15
4-й прыжок
кошки
28
11
5-й прыжок
кошки
20
7
6-й прыжок
кошки
12
3
7-й прыжок
кошки
4
L
Мышка успеет убежать от кошки.
101
щ і
196
разны е з а д а ч и
Лягушке до пруда 18 прыжков. Кошке
до лягушки 4 прыжка. За один прыжок
кошки лягушка делает 3 прыжка. Один
прыжок кошки равен 7 прыжкам лягуш­
ки. Догонит ли кошка лягушку, или ля­
гушка успеет спрятаться в пруду?
н е отры вая к а р ан д а ш а от б / м а ги
Пример 22
Можно ли, не отрывая карандаша от
бумаги и не проводя дважды по одной
линии, нарисовать следующий рисунок?
Если можно, приведите пример.
Решение.
Не отрывая карандаша от бумаги и не
проводя по одной линии дважды, мож-
102
РАЗНЫЕ ЗАДАЧИ і. §
но нарисовать рисунок, если он имеет не
больше двух узлов с нечётным количе­
ством исходящихлиний.
Например:
• в узле 8 исходящих линий
• в узле 5 исходящих линий^^ /
.
В задании нет нечётных узлов, поэтому
данный рисунок, не отрывая карандаша
и не проводя по одной линии дважды,
нарисовать можно.
103
Щ І
197
РАЗНЫЕ ЗАДАЧИ
Можно ли, не отрывая
УЧ
карандаша от бумаги и не
/
\
проводя дважды по одной
линии, нарисовать с л е д у - ________
ющий рисунок?
і
Можно ли, не отрывая
карандаша от бумаги и
не проводя дважды по
одной линии, нарисо­
вать следующий рису­
нок?
199
104
Можно ли, не отрывая
карандаша от бумаги и
не проводя дважды по
одной линии, нарисовать
следующий рисунок?
і
разны е з а д а ч и
і
I
3
Можно ли, не
отрывая каранда­
ша от бумаги и не
проводя дважды
по одной линии,
нарисовать следу­
ющий рисунок?
200
р а з д ел е н и е л и н и я м и и окружностями
Четырьмя линиями отделите цветы на
цветочной поляне друг от друга.
201
105
ho
РАЗНЫЕ ЗАДАЧИ
02
Четырьмя окружностями отделите ку­
бики друг отдруга.
СООТВЕТСТВИЯ
П р и м е р 23
Ира, Маша, Лиза и Паша заняли пер­
вые четыре места в городских соревно­
ваниях по шашкам. Определите, какое
место занял каждый из участников со­
ревнований, если:
• девочки не заняли первое место;
• Маша заняла второе или четвёртое
место;
• Ира и Маша не были последними.
106
РАЗНЫЕ ЗАДАЧИ і. §
Решение.
Составим таблицу.
1. Девочки не заняли первое место.
Место
Ира
Маша
Лиза
1
—
—
—
Паша
2
3
4
107
щ і
разны е з а д а ч и
2.
Паша.
Видим, что первое место занял
Место
Ира
Маша
Лиза
Паша
1
—
—
—
+
2
3
4
3.
Паша, заняв первое место, не мог
занятьдругое место.
Место
Ира
Маша
Лиза
Паша
1
—
—
—
+
2
—
3
—
4
—
4.
Маша заняла второе или четвёр­
тое место, значит, Маша не могла занять
третье место.
108
Место
Ира
Маша
Лиза
Паша
1
2
—
—
—
+
—
РАЗНЫЕ ЗАДАЧИ #. §
Место
Ира
3
Маша
Лиза
—
Паша
—
4
—
5.
Ира и Маша не были последними,
значит, девочки заняли не четвёртое ме­
сто.
Место
Ира
Маша
Лиза
Паша
1
—
—
—
+
2
3
4
—
—
—
—
—
—
б.
Из таблицы видно, что Маша заня­
ла второе место, а, значит, Ира и Лиза не
могли занять второе место.
Место
Ира
Маша
Лиза
Паша
1
—
—
—
+
2
—
+
—
—
3
4
—
—
—
—
—
109
Щ І
РАЗНЫЕ ЗАДАЧИ
7. Ира заняла третье место, а Лиза чет­
вёртое.
203
110
Место
Ира
Маша
Лиза
Паша
1
2
3
4
—
—
—
+
—
+
—
—
+
—
—
—
—
—
+
—
Дима, Вова, Миша и Ваня занимаются
футболом, теннисом, хоккеем и баскет­
болом. Каждый из мальчиков занима­
ется одним видом спорта. Определите,
каким видом спорта занимается каждый
из мальчиков, если:
• Дима занимается командным видом
спорта с мячом;
• Миша занимается индивидуальным
видом спорта;
• Ваня не занимается ни футболом, ни
хоккеем.
РАЗНЫЕ ЗАДАчИ #. §
Спорт
Дима
Вова
Миша
Ваня
Футбол
Теннис
Хоккей
Баскетбол
Костя, Рома и Сергей — друзья. Один
из них инженер, другой — программист,
третий — врач. Один из них любит путе­
шествовать, другой — читать, а третий —
рисовать. Костя учился в техническом
вузе. Врач пригласил своих друзей на х у ­
дожественную выставку, на которой вы­
ставили его работы. Профессия и увле­
чение Ромы начинаются с одной и той
же буквы. Определите, у кого из друзей
какая профессия и увлечение.
204
111
Щ І
РАЗНЫЕ ЗАДАЧИ
Имя
Профессия
Увлечение
Костя
Рома
Сергей
205
Ире, Полине, Лизе и Марине 5, б, 7 и
8 лет. На вопрос, сколько девочкам лет,
были даны следующие ответы:
• Ире 5 лет, Марине б лет;
• М а р и н е 6 ле т,Л и зе 7 ле т;
• Ире7 лет, Лизе 8 лет.
Определите, сколько лет каждой д е ­
вочке, если в любом утверждении одна
часть ответа правильная, а другая — нет.
Имя
Ира
Полина
Лиза
Марина
112
Возраст
РАЗНЫЕ ЗАДАЧИ і
«
ТЯжЁЛОЕ - ЛЁГКОЕ
Пример 24
Масса 7 яблок и 5 груш равна массе
9 яблок и 2 груш. Что тяжелее: 10 груш
или 7 яблок? Яблоки имеют одинаковую
массу, груши имеют одинаковую массу.
Решение.
7 яблок + 5 груш = 9 яблок + 2 груши.
Уберём справа и слева по 7 яблок и 2 гру­
ши.
3 груши = 2 яблока;
1 груша = I яблока.
Сравним 10 груш и 7 яблок.
Поскольку
1 груша = - яблока,
113
РАЗНЫЕ ЗАДАчИ
10 груш
= 1 03-= —3 = 6 -я
блок,
ГУ
3
значит, 7 яблоктяжелее 10 груш.
Ответ: 7 яблоктяжелее 10 груш.
206
Масса 12 абрикосов и 7 слив равна
массе 15 абрикосов и 3 слив. Опреде­
лите, что тяжелее: 14 слив или 11 абри­
косов?
ло ги ч ес к и е з а д а ч и
П р и м е р 25
Три брата — Гоша, Паша и Никита — ба­
ловались во время обеда, и кто-то из них
разбил чашку с блюдцем. Никита сказал:
«Чашку разбил Паша». Гоша сказал: «Это
не я разбил чашку». Впоследствии вы­
яснилось, что одно из этих утверждений
является верным, а другое утверждение
не верно. Кто из братьев разбил чашку?
114
РАЗНЫЕ ЗАДАЧИ і
« *з e w *
Щ Щ ш
Решение.
Предположим, что Никита прав, и чаш­
ку с блюдцем разбил Паша. Тогда прав и
Гоша, который сказал, что разбил не он.
Это противоречит условию задачи. По­
лучаем, что прав Гоша, и это не он раз­
бил чашку с блюдцем, а Никита не прав,
а значит, не Паша разбил чашку с блю д­
цем, а Никита.
Три сестры — Оля, Маша и Наташа —
собрали корзинку грибов. Дома девочки
сосчитали общее количество собранных
грибов. Оля сказала: «М ы собрали боль­
ше 32 грибов». Маша сказала: «В корзин­
ке меньше 24 грибов». Наташа сказала:
«Собрано не больше 26 грибов». Одна
из девочек при подсчёте ошиблась. Ка­
кое наибольшее количество грибов мог­
ло лежать в корзинке? Определите, какая
девочка ошиблась?
207
Lb
115
208
116
Брат в три раза старше сестры и в че­
тыре раза младше отца. Когда отцу будет
44 года, он будет старше дочери в че­
тыре раза. Мать младше отца на 2 года.
Определите текущий возраст каждого
члена семьи?
_ _
ОТВЕТЫ
1 8 6 9
1 3 7 4
.
9 8 6 1
7 7
1. 99.
2. 4, у этого робота количество кно­
пок внизу туловища на 1 меньше, чем у
остальных роботов.
3. а) 3; б) 2.
4. 21.
5.
117
7
18 6 9
о тв еты
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
т Р И БМ Д Н Е К А Л Я В С П О У
М Е
Д И У С
Н
НУС
К
У М М А
В
.п
П
М Б
ВЕК
М И л л и о н
п
и
О Р
И
П Е
н
иМЕР
ИМ Е
ином
и
КВА
118
Р А Т
ОТВЕТЫ
1 8 6 9
>±±
_ 9 8 6 1
7.
119
7
18 6 9
ОТВЕТЫ
8.
1 В 0 с Е м ь
2 К В А
Р А т
3 0 т р Е 3 0 к
4 С Л 0 Ж Е н И Е
5 п Е р И М Е т Р
6 г р А Д У С
7 с Т 0
8 м И н У с
И р к У л ь
9
10 ч А с т н 0 Е
д
ц
9. Девять.
120
ОТВЕТЫ
1 8 6 9 _ 9 8 6 1
4 9 5
g 7 8 4
1 3 7 4
7 7
10.
11
12. 5 ,8,1 1, 14, 17, 20, 23.
121
18 6 9
4 9 5
13 7 4
ОТВЕТЫ
23 ЬН
4. mЧ
і__j
г~Р
і_і
□
СОНЮ
8.
122
BFBFBP
iг_-_Рi
0
24. !g|
ЯЛ
25 Ш -І
VI/
26. •
—J
27Б
28В
29. 4 S
30. ,=
>L{
© ©
и
31-£0
сР ®о
гш
32-40
зз- ЗБ
34. ф у Т
46. |+ ІХ=ѴІ + IV
35. Ш Е С Т Ь
47. Х + ІІ = XII
36. М Е Т Р
48. X— Ѵ-4-ІІ = VII
37. CTQPDHR
49. 3+5=0
38. СТЕПЕНЬ
50. 5+4=9
39. VI —1¥= ІІ
51- ЕЬЕНи
40 . х і + ѵ - і х = : ѵ і 52. g g = g g
41. VII —-III — IV
53. П 5 І Т Ь
42. |X + V! = XV
54. XVIII
43. X — IV — VI
55. 3
44. VI + II + 1= IX 56. К О Т
45. I + II! = IV
57.
осень
1 23
18 6 9
4 9 5
13 7 4
оТВЕТы
58. Сумма равна 57.
59. Сумма равна 110.
60.
26 51 20 45 14 39
9
8
27 52 21 46 15 33
34 10 28 53 22 40 16
17 35 11 29 47 23 41
42 18 36
5
25 43 12 37
30 48 24
6
50 19 44 13 38
124
31 49
7
32
ответы
1 8 6 9
>±±
_ 9 8 6 1
61
62.
63.
64.
65. 2.
66 . 4.
67. 3.
68 . 3 .
125
7
18 6 9
13
7 4
69. 1.
70. 4.
71. 4.
72. 28.
73. 38.
74. 32.
75. 28.
76. Снизу 1, слева б.
77. Слева 4, справа 2.
78. 1 и 4.
79. 5 и 6 .
80.
81
126
ОТВЕТЫ
ОТВЕТЫ
1 8 6 9
>±±
_ 9 8 6 1
82.
83.
84.
85.
86.
87.
88.
127
7
89.
90.
91.
92.
128
18 6 9
ОТВЕТЫ
ОТВЕТЫ
1 8 6 9
>±±
_ 9 8 6 1
Нет, нельзя. Фигурку вида
сумма чисел в клетках которой равна 28,
можно составить из двух фигурок вида
^ — I ^—і—^ , сумма чисел в клетках кото­
рых будет равна 17 + 17 = 34, а при
наложении этих фигур в прямоугольни­
ке суммы должны совпадать.
93.
Нет, нельзя. Прямоугольник 4x12
можно замостить двенадцатью фигурка­
ми вида м м или шестнадцатью ф и гур ­
ками вида ггг. Если весь прямоугольник
4x12 клеток замостить фигурками вида
м м , то сумма всех чисел должна быть
равна 12 • 18 = 216, а если расставить
фигурки вида ггг. то сумма всех чисел
должна быть равна 16 • 11 = 176. Ви­
дим, что суммы не совпадают, значит, та­
кого быть не может.
94.
95.
129
_1_ _5_ _1_ _5_ _1_
7
18 6 9
_5_ _1_ _5_ _1_ _5_
15 15 1
ГГ”
130
ОТВЕТЫ
ОТВЕТЫ
1 8 6 9
>±±
_ 9 8 6 1
97. Нельзя, так как прямоугольник 7x5
состоит из 35 клеток, а 35 не делится на­
цело на 2.
98.
99.
100 . 1 .
101 . 3 .
102 . 3 .
103. 4.
131
__LJL_LJL
7
_LJL_LJL А.
18 6 9
_5_ _1_ _5_ _1_ _5_
_L_5__L_5__L
5 15
15
ОТВЕТЫ
104. 60.
105. 90.
106. 990.
107. 9865321074.
108. 102348.
109. 9999992.
110. 10000035.
111. 10236.
112. 648.
113. 759.
6; 2. Число делится на 8, значит,
число, образованное последними тремя
цифрами данного числа, делится на 8.
«03...» делится на 8, если это 032. По­
следняя цифра 2. Сумма всех цифр числа
равна 28, значит, определим недостаю­
щую цифру: 2 8 - 7 - 4 - 1
- 5 ­
- 0 - 3 - 2 = 6. Код: 74156032.
114.
Число делится на 15, значит, оно
делится на 5. Число делится на 5, если
оканчивается на 5 или 0. Поскольку чис­
ло также делится на 18, оно делится на
115.
132
1 8 6 9
ОТВЕТЫ
>±±
_ 9 8 6 1
2 и на 9. Число делится на 2, если окан­
чивается на 0, 2, 4, 6, 8. Получаем, что
число оканчивается на 0. Число делится
на 9, если сумма цифр делится на 9 : б +
+ 8 + 2 + 4 + 7 + 6 + 4 + 0 = 37.
К 37 нужно добавить 8, чтобы сумма
цифр делилась на 9 (37 + 8 = 45, 45
делится на 9). Пароль: 688247640.
116. (77 - 7 ) : (7 + 7) = 5.
117. 5 • 5 • 5 - 5 • 5 = 100.
118. 33 : 3 - 33 : 33 = 10.
119. 1 + 2 - 3 + 4 - 5 + 6 + 7 -8=11.
120 . 88 + 8 - 8 + 8 + 8 + 8 + 8 +
+ 8 + 8 = 200.
1 2 1 . 222
:
2 - 22 : 2 = 1 0 0 .
122. (10 + 1 0 + 1 0 + 1 0 +
10) х
х 1 0 : ( 1 0 : 1 0 ) = 5.
123. 4 + 4 + 4 - 4 + 4 : 4 - 4 = 21.
124. (3 + 5) : 8 + (3 + 5) : 8 + 3 = 5.
125. 6 0 : ( 1 2 + 3) + 2 • 24 = 52.
126. 2 2 : 2 + 9 -
3 - 5 = 5.
133
7
18 6 9
127. 3 + 9 9 : 1 1 128. 143 -
ОТВЕТЫ
10 = 2.
1 13 - 22 = 8.
129. 17 + 28 + 79 = 124.
130. 153 = 1 12 + 35 + 6.
131. а) + 23 93 75
132.
133.
6 3 2
2 6 7
9 9 8
2 2 6 5
18 6 9
4 9 5
а)
1 3 7 4
1 6
X
5 8
а)
1 2 8
4і
8 0
9 2 8
9 8 6 1
9 7 8 4
7 7
6 5
х 98
5
О
8
6 3 7 0
б) +
б)
б)
6 7 6 8 9 4
6 5 8
7 2
1 8 8
1 8 8
0
134. а) _ 3 6 5 5 4 3
3 4 4
8 5
2 1 5
2 1 5
О
135.
136.
\ +б 3 1 8
а;
6 3 18
12 6 3 6
в)' 9010
8 111
8 99
d U 4 35 2
в) 4 3 5 2
87 04
30003 , 300003 , 3000003 .
137. 288, 576, 1 152 ( 9 * 2 = 18;
18 • 2 = 36;36 • 2 = 72;
134
ОТВЕТЫ
1 8 6 9
>±±
_ 9 8 6 1
72 ■ 2 = 144; 144 2 = 288; 288 3 =
= 576; 576 • 2 = 1152).
138. 15, 20, 18 (6 + 5 = 1 1;
11 - 2 = 9; 9 + 5 = 1 4 ; 1 4 - 2 = 12;
12 + 5 = 1 7 ; 1 7 - 2 = 1 5 ; 1 5 + 5 =
= 20; 2 0 - 2 = 18).
139. 96,48, 192( 3 •4 = 12; 12 : 2 =
= 6; 6 4 = 24; 24 : 2 = 12; 12 • 4 =
= 48; 48 : 2 = 24; 24 ■4 = 96; 96 : 2 =
= 48;48 4 = 192).
140. 8 1 , 6 4 , 4 9 ( 1 3 2 = 169; 122 = 144;
112 = 121; 102 = 100; 92 = 81; 82 =
= 64; 72 = 49).
141. 365, 1094( 2 - 3 - 1 = 5;
5 • 3 - 1 = 14; 14 • 3 - 1 = 41;
41 • 3 - 1 = 122; 1 2 2 - 3 - 1 = 365;
365 ■ 3 - 1 = 1094).
142. 324, 972 (4 - 3 = 12; 12- 3 = 36;
36 •3 = 108; 108- 3 = 324; 3 2 4 - 3 =
= 972).
143. 144, 288, 576 (4 + 5 = 9; 4 +
+ 5 + 9 = 18; 4 + 5 + 9 + 18 = 36;
135
7
18 6 9
ОТВЕТЫ
4 + 5 + 9 + 18 + 36 = 72; 4 + 5 +
+ 9 + 18 + 36 + 72 = 144; 4 + 5 +
+ 9 + 18 + 36 + 72 + 144 = 288;
4 + 5 + 9 + 18 + 36 + 72 + 144 +
+ 288 = 576).
144. 57, 77,100 (2 + 5 = 7 ;7 + 8 =
= 15; 15 + 11 = 26; 26 + 14 = 40;
40 + 17 = 57; 57 + 20 = 77; 77 +
+ 23 = 100).
145. 1, 2, 5 (13 = 1; 23 = 8; З3 = 27;
43 = 64; 53 = 125).
146. 73,62,49(98 -
1 = 97; 97 - 3 =
= 94; 94 - 5 = 89;89 - 7 = 82;
82 - 9 = 73; 73 - 11 = 62; 62 - 13 =
= 49).
147. 144, 147, 441 (1 + 3 = 4; 4 х
х З = 12; 12 + 3 = 15; 15 3 = 45;
45 + 3 = 48; 48 • 3 = 144; 144 +
+ 3 = 147; 147 3 = 441).
1296, 2401 (14 = 1;24 = 16; З4 =
= 81; 54 = 625; б4 = 1296;74 = 2401).
148.
136
ОТВЕТЫ
1 8 6 9
>±±
_ 9 8 6 1
149. 47, 76, 123 (3 + 4 = 7; 4 + 7 =
= 1 1 ; 7 + 1 1 = 1 8 ; 1 1 + 18 = 29;18 +
+ 29 = 47; 29 + 47 = 76; 47 + 76 =
= 123).
150. 70,84, 99 (7 + 8 = 15; 15 + 9 =
= 24; 24 + 10 = 34; 34 + 11 = 45;
45 + 12 = 57;57 + 13 = 70;70 + 14 =
= 84; 84 + 15 = 99).
151. 105, 192, 353 (5 + 6 + 7 = 18;
6 + 7 + 18 = 31; 18 + 31 + 56 =
= 105; 31 + 56 + 105 = 192; 56 +
+ 105 + 192 = 353).
155, 21 5, 285 (5 + 10 = 15;
15 + 20 = 35; 35 + 30 = 65; 65 +
+ 40 = 105; 105 + 50 = 155; 155 +
+ 60 = 215; 215 + 70 = 285).
152.
153. 9 , 2 0 , 8 (14 + 15 -
13 = 16;
15 + 1 3 - 1 6 = 12; 13 + 1 6 - 1 2 =
= 1 7 ; 1 6 + 1 2 - 1 7 = 11; 12 + 1 7 - 1 1 = 1 8 ; 1 7 + 1 1 - 1 8 = 10;11 +
+ 1 8 - 1 0 = 1 9 ; 1 8 + 1 0 - 1 9 = 9;
137
7
18 6 9
ОТВЕТЫ
10 + 19 - 9 = 20; 19 + 9 - 20 = 8).
154. 39( 18 + 15 = 33; 33 + 15 = 48;
24 + 15 = 39; 39 + 15 = 54).
154. 39.
155. 8 (4 х 23 = 92; 12 х 8 = 96).
156. 27 (1 + 7 + 9 =
17; 4 + 8 +
+ 15 = 27).
157. 4 (785 - 243 = 542).
34, 78 (В числах цифры меняем
местами. Верхний ряд: 38, 39, 40, 41,
42, 43; нижний ряд: 92, 91, 90, 89, 88,
87).
158.
159. 32(3 •4 = 12; 5 - 4 = 20; 12 - 4 =
= 48; 8 - 4 = 32).
160. 127( 7 ■2 + 1
= 15;15 •2 + 1 =
= 31;31 - 2 + 1 = 63; 63 -2 + 1 = 127).
161. 15 (3 + 18 = 21; 10 + 11 = 21;
4 + 1 7 = 2 1 ; 6 + 1 5 = 21).
162. 536 (18; 19; 20; 21; 22; 23 и 31;
32; 33; 34; 35; 36).
138
ОТВЕТЫ
1 8 6 9
>±±
_ 9 8 6 1
163. 19( 25 - 1 = 24; 31 - 7 = 24;
37 - 13 = 24; 43 - 19 = 24).
164. 81 ((1 + 4)2 = 25; (2 + 7)2 = 81).
165. 7( ( 1 + 6 + 5 + 14) - (1 + 2 +
+ 3 + 4 ) = 16; (4 + 20 + 6 + 1 5 ) - ( 8 + 11 + 10 + 9) = 7).
166. 82((1 - 2- 3- 5) + (1 - 4 - 3 - 7 ) = 114;
( 3 - 3 1- 2) + (1 - 2 - 4 - 8 ) = 82).
167. 16(1 + 14 + 8 + 7 + 1 5 + 6 = 51;
3 + 21 + 9 + 5 + 1 8 + 1 6 = 72).
168. 30( 12 + 14 = 26; 15 + 18 = 33;
1 9 + 11 = 30).
169. 720 (1 - 2 = 2;2 • 3 = 6;
6 •4 = 24; 24 •5 = 120; 120 •6 = 720).
170. 26( 7 + 3- 1 = 10; 10 + 3 - 2 =
= 16; 16 + 3- 3 = 25; 25 + 3 ■4 = 37;
8 + 4- 1 = 1 2 ; 1 2 + 4 •2 = 20;20 +
+ 4 •3 = 32; 32 + 4 •4 = 48; 11 +
+ 5 -1 = 16; 16 + 5 - 2 = 26; 26 +
+ 5 3 = 41; 41 + 5 - 4 = 61).
171. 96( ( 3 + 4) - (8 + 1) = 63;
(6 + 2) •(7 + 5) = 96).
139
_i__LJL
_LJL
5__LJLA.
_5_ _1_ _5_ _1_ _5_
_L_5__L_5__L
5 15 15
7
5_
2
"
18 6 9
4 9 5
13 7 4
172. Петя не прав. Правильное число 46
(14 + 8 = 22; 22 + 8 = 30; 30 +
+ 8 = 38; 38 + 8 = 46).
173. Нет, не мог. Цена каждый из шести
игрушек - число нечётное. Сумма шести
нечётных игрушек — число чётное, а 383
является нечётным числом.
174. Нет, не могло. Каждая из четырёх
девочек вырезала нечётное число сне­
жинок, а сумма четырёх нечётных чисел
является чётным числом.
175. Нет, не могло. Каждая из трёх дево­
чек собрала нечётное число цветов. Сум­
ма трёх нечётных чисел является числом
нечётным, а Ю О — число чётное.
176. Сумма трёх нечётных чисел являет­
ся нечётным числом, а 120 — число чёт­
ное.
177. Суммачётная, 15050.
178. У Юли 18, 1, 23, 5.
179. Нет, не может. Возьмём какого-
нибудь продавца. Для того чтобы вы-
140
8
6 9 _ 9 8 6 1
4 9 5
1 3 7 4
9 7 8 4
7 7
полнить условие задачи, он должен по­
очередно отработать с 22 коллегами,
причём каждый раз он выходит на ра­
боту с четырьмя новыми продавцами,
а поскольку 22 не делится нацело на 4,
такого быть не может.
180. Нет,неможет.
181. Нет, не права.
182. Раскрасим доску в серый и белый
цвета. Получилось 13 серых и 12 белых
клеток. За один ход 13 фишек, стоящие
на серых клетках, встанут на белые и мо­
гут занять все белые клетки, а вот 12 ф и ­
шек, стоящие на белых клетках, не могут
встать на 13 серых так, чтобы все серые
клетки были заняты.
141
7
18 6 9
ОТВЕТЫ
183. Первоначальная сумма чисел рав­
на 35. Прибавляя каждый раз к двум
числам 3, сумма будет оставаться нечёт­
ной, а сумма четырёх одинаковых чисел
является чётным числом, значит, такого
быть не может.
184. Сумма натуральных чисел от 15до
24 равна 195, число нечётное. Если ме­
нять в выражении « + » на « - » , чётность
не поменяется, сумма останется нечёт­
ной, а число 2 является чётным, значит,
такого быть не может.
185. Нет, не могли. Количество решён­
ных примеров у детей, сидящих по со­
седству, отличается на 1, значит, если у
одного ребёнка решено чётное количе­
ство примеров, у соседей будет реше­
но нечётное число. Шесть детей решили
чётное и шесть нечётное число приме­
ров. Общая сумма чётная, а 77 — число
нечётное.
186. Нет, не может. Количество кубиков,
из которых составлены соседние баш-
142
ОТВЕТЫ
1 8 6 9
>±±
_ 9 8 6 1
ни, отличается на чётное число кубиков,
а первая башня состоит из трёх кубиков,
поэтому каждая башня состоит из нечёт­
ного числа кубиков, а сумма пяти нечёт­
ных чисел является числом нечётным,
а54 — чётное число.
187. ( 1 8 : 6 + 31) •4 + 23 = 159.
188. ( ( 7 4 -4 0 ) : 17 + 1 ) • 11- 15 = 18.
189. ((38 •2 - 4 1 ) •3 + 4 5 ) : 2 - 5 0 = 25.
190. 9584.
191. 10542.
192. 85953.
193. 57382.
194. 836.
195. 23 и 32.
196. Лягушка успеет спрятаться от кош­
ки в пруду.
143
7
18 6 9
ОТВЕТЫ
Расстояние
от кошки
до лягушки
Расстояние
отлягушки
до пруда
Сначала
28
18
1-й прыжок
кошки
24
15
2-й прыжок
кошки
20
12
3-й прыжок
кошки
16
9
4-й прыжок
кошки
12
6
5-й прыжок
кошки
8
3
6-й прыжок
кошки
4
Пруд
Рисунок имеет 8 узлов с нечётным
количеством исходящих линий, поэтому,
не отрывая карандаша от бумаги, такой
рисунок изобразить нельзя.
197.
144
198. Рисунок имеет 4 узла с нечётным
количеством исходящих линий, поэтому,
не отрывая карандаша от бумаги, такой
рисунок изобразить нельзя.
199. Рисунок не имеет узлов с нечётным
количеством узлов, поэтому, не отрывая
карандаша от бумаги, такой рисунок изо­
бразить можно.
Рисунок имеет 18 узлов с нечётным
количеством исходящих линий, поэтому,
не отрывая карандаша от бумаги, такой
рисунок изобразить нельзя.
200.
201 .
145
203.
Спорт
Дима
Вова
Миша
Ваня
Футбол
+
—
—
—
Теннис
—
—
+
—
Хоккей
—
+
—
—
Баскетбол
—
—
—
+
204.
146
Имя
Профессия
Увлечение
Костя
инженер
чтение
Рома
программист
путешествия
Сергей
врач
рисование
1 8 6 9 _ 9 8 6 1
4 9 5
9 7 8 4
1 3 7 4
7 7
205.
Имя
Возраст
Ира
7
Полина
8
Лиза
5
Марина
б
206. 11 абрикосовтяжелее 14слив.
207. 23, Оля ошиблась.
208. Дочери 3 года, сыну 9 лет, матери
34 года, отцу Зблет.
147
ЛИТЕРАТУРА
1. Генкин С. А., Итенберг И. В., Фомин Д. В.
Ленинградские математические кружки: по­
собие для внеклассной работы. - Киров:
АСА, 1994. - 272 с.
2. Инфоурок [Электронный ресурс]. URL:
https://infourok.ru.
3. Улицкий А. Т., Улицкий Л. А. Игры со
спичками. - Минск: «ВУАЛ», 1993. - 96 с.
4. Шарыгин И. Ф., Шевкин А. В. Задачи на
смекалку. - М.: Просвещение, 2010. - 95 с.
148
*ЫіѴ®
www.bhv.ru
Баррет P., Оскей У.
Домашняя лаборатория
для занимательных опытов
О тдел о п т о в ы х п о ста в о к
E-mail: opt@ bhv.spb.su
Соберите более 200 приборов
и проведите более 1600 научных экспериментов!
Книга Раймонда Барретта «Домашняя ла­
боратория для занимательных опытов»
решала смелую задачу: рассказать читате­
лям, как оборудовать домашнюю лабора­
торию, сконструировать приборы для ис­
следований по химии, биологии и физике и
провести с их помощью эксперименты.
Некоторые инструкции и опыты могут
показаться рискованными по современным
меркам, но многие представители преды­
дущих поколений с нежностью вспомина­
ют, какое значение придавали научным
исследованиям раньше.
Современная версия книги, дополненная комментариями и примечания­
ми Уинделла Оскея, покажет, как провести научные исследования
в школе, дома или на работе.
С помощью книги вы смастерите:
•
•
•
•
•
•
•
•
•
собственную лабораторную посуду;
камеру Вильсона для обнаружения космического излучения;
микроскопы с увеличением от 25х до 160х;
барометры, термометры и гигрометры;
магниты, моторы, батареи и конденсаторы;
микротом, анемометр и сейсмограф;
телескоп, спектроскоп и нефоскоп;
генераторы кислорода и водорода;
гелиограф Кэмпбелла - Стокса.
Смастерив приборы, вы сможете провести более 1600 экспериментов,
описанных в книге: добыть водород, вырастить кристаллы, обнаружить
жизнь в капле воды, измерить все (от массы до электропроводности,
скорости метаболизма или космического излучения), создать электриче­
ский двигатель и отслеживать спутники Юпитера!
Рубанцев В.
www.bhv.ru
Развивающие головоломки
Для юных капитанов
О тдел о п т о в ы х п о ста в о к
E-mail: opt@ bhv.spb.su
Книга предназначена для интеллектуального досуга детей млад­
шего и среднего школьного возраста, старшие могут использо­
вать ее как тренажер умственных способностей. Она развивает
внимание, наблюдательность, память, сообразительность, сме­
калку, логическое мышление, целеустремленность, самостоя­
тельность и самоконтроль, аккуратность и обучаемость. В ней
собраны самые популярные современные головоломки на мор­
скую тему: Морской бой, Маяки, Боевые маяки, Морской сапёр.
Для каждого типа задач приведены цветные схемы, иллюстри­
рующие правила и приемы решения. Всего в книге 115 задач,
представленных в виде морских карт, составленных вручную
и тщательно проверенных. Ответы к заданиям даны в конце
книги.
Валерий Д митриевич Рубанцев, автор книг «Хитори: круче, чем судоку» и «Самоучитель Delphi в примерах, играх и программах», член
Клуба ценителей головоломок «Диоген», автор многочисленных голово­
ломок, опубликованных в периодических изданиях: «Поле чудес»,
«Кроссворд-мастер», «Кроссворд-шоу» и др., ведущий занимательных
газетных рубрик: «Знайка» — для детей и «Умницы и умники» — для
взрослых.
Рубанцев В.
^ bhv
www.bhv.ru
Друдлы, пятна Роршаха
и другие загадочные картинки
О тдел о п т о в ы х п о ста в о к
E-mail: opt@ bhv.spb.su
Линейка, ручка, карандаш
Помогут взять на абордаж
Загадки, пазлы, друдлы.
Весело — не трудно!
Книга предназначена для интеллектуального досуга детей младшего
и среднего школьного возраста, старшие могут использовать ее как
тренажер умственных способностей.
В ней собраны рисованные загадки, которые редко встречаются
в подобных изданиях: друдлы, друделки друдлы-самоделки , пятна
Роршаха, фотозагадки, чудесные превращения клякс и кофейных
пятен. Они не имеют однозначных отгадок и потому будоражат во­
ображение, развивают фантазию, творческие способности, нестан­
дартное мышление, умение находить неожиданное, парадоксальное
решение. Особый интерес представляют загадочные картинки: паз­
лы и фотопазлы, фотофрагменты и фотосессии, мандалы и раскрас­
ки, прятки мурмелей и жучиная охота на крендель-брецель. Есть
в книге и традиционные ключворд, чайнворд, маскировочная сетка
для зверушек и другие задания.
Варианты ответов даны в конце книги.
Валерий Дмитриевич Рубанцев, автор книг «Хитори: круче, чем судоку»,
«Самоучитель Delphi в примерах, играх и программах», «Развивающие го­
ловоломки для юных капитанов», член Клуба ценителей головоломок «Дио­
ген», автор многочисленных головоломок, опубликованных в периодиче­
ских изданиях: «Поле чудес», «Кроссворд-мастер», «Кроссворд-шоу» идр.,
ведущий занимательных газетных рубрик: «Знайка» — для детей
и «Умницы и умники» — для взрослых.
,bhv®
Сесери К.
Необычные вещи из обычной бумаги
www.bhv.ru
О тдел о п т о в ы х п о ста в о к
E-mail: opt@ bhv.spb.su
Измените свое отношение к бумаге, и она изменит вашу жизнь!
Бумага — это фантастический матери­
ал. Она легко режется, но при этом
обладает невероятной прочностью. Ее
легко повредить, но также она может
храниться веками. Она может быть
жесткой, как доска, подвижной, как
пружина, или плавать, как лодка. Ее
изобретение навсегда изменило мир.
Книга идеально подходит для детей,
родителей и преподавателей. Она по­
строена на реальных проектах, содер­
жит цветные иллюстрации, подробные
инструкции, списки материалов и шаб­
лоны, — и все это позволит читателю
реализовать описанные в книге проекты или придумать что-то со­
вершенно новое. Создание забавных конструкций из бумаги увлечет
и заинтригует каждого, от новичков и до опытных мастеров.
Вы узнаете, как изготовить:
съедобную рисовую бумагу, прекрасно подходящую для секретных
сообщений
бумажные электрические схемы, выключатели и датчики
бумажную кошку со светящимися глазами
бумажный генератор, вырабатывающий электрический ток
планетоход, движущийся благодаря механизмам из бумаги
плоские бумажные модели, которые при нагреве раскрываются
и становятся объемными
домик-купол из газет, в который можно забраться и играть.
Вы познакомитесь с историей изготовления бумаги и научитесь созда­
вать, применяя творчество и выдумку, свои собственные забавные и не­
обычные конструкции из бумаги.
К эти Сесери является автором забавных и познавательных книг для детей
и семейного чтения.
Т ур С., Б о куч а в а Т.
Учебник-тетрадь
по информатике для 5 класса
Учебник-тетрадь
по информатике для 6 класса
Г р иф К ом итета по о б р а зо в а н и ю С а н кт-П е те р б ур га
152 с., ISBN 978-5-94157-985-3
148 с., ISBN 978-5-94157-986-0
1алгоритмы
и исполнители
Знакомство
с MS Word
1знакомство
с компьютером
Знакомство
с MS Power Point
1знакомство
с ОС Windows
Знакомство
с объектно­
ориентированной
средой програм­
мирования Visual
Basic
1стандартные
приложения
W indows: Блокнот,
Калькулятор, Paint
Методическое пособие по информатике
для учителей 5-6 классов. 2-е изд.
Г р иф К ом итета по о б р а з о в а н и ю С а н кт-П е те р б ур га
448 с., ISBN 978-5-94157-984-6
• Программа курса
• Тематическое и поурочное планирование
• Ответы и решения
• Контроль и оценка результатов
• Электронное пособие на CD
Учебники-тетради для 5-го и 6-го классов и методическое пособие для учителей
5 -6 классов являются частью учебно-методического комплекта по информатике
и информационно-коммуникационным технологиям для общ еобразовательных
школ. Содержания учебников-тетрадей и методического пособия соответству­
ют общепринятой концепции содержания пропедевтического курса инф ормати­
ки в 5 -6 классах с учетом возрастных особенностей.
Т ур С ветлана Н иколаевна, педагог с 18-летним стажем. За заслуги в области
образования награждена нагрудным знаком «Почетный работник образования
Российской Федерации». Автор курса по информатике для общ еобразователь­
ной школы и многочисленных публикаций по методике преподавания инф орма­
тики в школе. Включена в энциклопедию «Лучшие люди России».
С
w w w .b h v .ru
Б о к у ч а в а Т атьяна П етровна, педагог с 13-летним стажем, при­
зер и лауреат Всероссийских образовательных конкурсов и проектов. Автор курса инф орматики для общеобразовательных школ
и публикаций по методике преподавания инф орматики в школе
в специализированных педагогических изданиях.
Отдел оптовы х поставок: E-mail: opt@bhv.spb.su
Дуванов А. и др.
АЗЫ
ПРОГРАММИРОВАНИЯ
АЗЫ ПРОГРАММИРОВАНИЯ.
Факультативный курс. Книга для ученика
Гриф Комитета по образованию
Санкт-Петербурга
352 с., ISBN 978-5-9775-3541-0
Теоретические основы программирования излагаются в нагляд­
ных средах исполнителей Кукарача и Корректор, сложные темы
становятся простыми и ясными. Особое внимание уделяется
основам формализации и построения алгоритмов, тестированию
и отладке программ. Целый раздел посвящен принципам постро­
ения трансляторов. Программные среды исполнителей помеще­
ны на диске, прилагаемом к книге учителя из этого комплекта,
который также содержит решения всех задач и дополнительные
материалы к урокам. Закрепить практический опыт программи­
рования поможет книга «Азы программирования. Задачник».
Дуванов А. и др.
АЗЫ
ПРОГРАММИРОВАНИЯ
АЗЫ ПРОГРАММИРОВАНИЯ.
Факультативный курс. Задачник
160 с., ISBN 978-5-94157-288-5
В книге собраны задачи, которые предлагались на сетевых
турнирах курса «Азы программирования» Роботландского уни­
верситета. Представлены задачи различной тематики: поиск и
сортировка, нахождение экстремума, разнообразные подсчеты,
логические и геометрические задачи; традиционный наиболь­
ший общий делитель и Ханойская башня; нетрадиционные для
школьников рекурсивные определения Бэкуса— Наура, запись
выражения по-польски, стековые вычисления, синтаксический
анализ и построение трансляторов. Задачи ориентированы на
программирование в среде исполнителей Кукарача и Корректор,
подробное описание которых содержит книга «Азы программи­
рования. Книга для ученика».
Дуванов А. и др.
АЗЫ
ПРОГРАММИРОВАНИЯ
АЗЫ ПРОГРАММИРОВАНИЯ.
Факультативный курс. Книга для учителя (+CD-ROM)
496 с., ISBN 978-5-94157-584-8
w w w .b h v.ru
В книге обобщен уникальный многолетний опыт Роботландского
сетевого университета по обучению детей программированию.
Материал излагается в стиле курса «Азы информатики» и зна­
чительно расширяет и углубляет тему программирования, кото­
рая в базовом курсе нацелена на общеобразовательные задачи.
Повышенное внимание уделяется основам формализации и по­
строения алгоритмов, тестированию и отладке программ. Под­
робно рассмотрены алгоритмические конструкции: циклы двух
видов, ветвление, применение процедур, рекурсия; целый раз­
дел посвящен принципам построения трансляторов. Изложена
методика проведения занятий и турниров по программирова­
нию. Прилагаемый компакт-диск содержит программные среды
исполнителей и решения всех заданий учебника и задачника.
Отдел оптовы х поставок: E-mail: opt@bhv.spb.su
Дунаев В.
^bhv®
Занимательная математика.
Множества и отношения
w w w .b h v.ru
Отдел о птовы х поставок:
E-mail: opt@bhv.spb.su
336 с., ISBN 978-5-94157-988-4
П ро сто и д о с т у п н о о л о ги к е и м ы ш л е н и и
ВадимДун*#*
Занимательная
математика
МНОЖЕСТВА И ОТНОШЕНИЯ
«
Г
«...Э та книга о математике не для математиков. Она адресована всем, кто лю ­
бит поразмышлять или порешать задачки и, в первую очередь, тем, кто причис­
ляет себя к людям гуманитарной направленности, чуждым точным наукам —
психологам, социологам, юристам, журналистам, врачам, биологам и т. п.,
а также школьникам старш их классов. Для чтения этой книги не предполагает­
ся сколько-нибудь серьезная математическая подготовка, знаний в пределах
средней школы, даже изрядно подзабытых, вполне достаточно.
Самым занимательным в математике является, пожалуй, не столько интри­
гующ ие и увлекательные ф ормулировки задач и неожиданные ответы на них,
сколько порой драматический поиск решений, собственно мыслительный про­
цесс. Правильный ответ, конечно, важен, но это не главная цель данной книги.
Я хотел бы акцентировать внимание на пути к цели, а не на конечной точке
путеш ествия...»
В. Дунаев, автор книги
Д унаев В адим В яч е сл а в о в ич , канд. техн. наук, специалист в области компью­
терных инф ормационных технологий. Автор более десятка популярных книг:
«Сам себе W eb-дизайнер», «HTML, скрипты и стили», «Основы W eb-дизайна»,
«Сценарии для W eb-сайта. PHP и JavaScript», «Базы данных. Язык SQL» и др.
^Ьпѵ®
w w w .b h v.ru
Голиков Д.
Scratch для юных программистов
192 с., ISBN 978-5-9775-3739-1
Отдел о птовы х поставок:
E-mail: opt@bhv.spb.su
С делай св о ю и гр у!
Д ети н а учатся:
• работать в графическом редакторе;
• редактировать звуки;
• создавать мультфильмы;
• создавать игры;
• сохранять созданные проекты.
Д ети у з н а ю т:
• о логических и математических операторах;
• о циклах и условиях;
• о списках;
• о координатной плоскости;
• о процентах и градусах.
Рассказано, как скачать и установить Scratch, написать первую программу,
мультфильм и игру. Приведены примеры создания более сложных мультфиль­
мов и компьютерных игр. Дети научатся создавать и сохранять проекты, рабо­
тать в графическом редакторе, озвучивать фильмы, использовать логические
операторы, циклы, условия, списки и другие элементы программирования. По­
путно они узнают про координатную плоскость, проценты, десятичные дроби,
градусы и другие математические понятия.
Голиков Д.
40 проектов на Scratch
для юных программистов
192 с., ISBN 978-5-9775-3939-5
Книга написана на основе опыта обучения про­
граммированию на языке Scratch в кружке юных
программистов и протестирована на сотне детей
7 -1 2 лет. Материал рассчитан на самостоятельное,
без помощи взрослых, изучение Scratch школь­
никами 2 -5 классов, имеющими базовые навыки
управления компьютером. Доходчивость изложения
позволит детям сразу начинать создавать увлека­
тельные проекты, а присущий автору юмор сделает это занятие веселым. Боль­
шое количество проектов и заданий для креативной самостоятельной работы
поможет творчески применять многочисленные возможности Scratch.
Юные программисты узнают о логических и математических операторах, цик­
лах и условиях, научатся создавать забавные рисунки и узоры, музыкаль­
ные проекты, мультфильмы и веселые игры под Android и даже продавать их
в магазинах приложений.
tbhv®
w w w .b h v .ru
Отдел о птовы х поставок:
E-mail: opt@bhv.spb.su
Винницкий Ю., Григорьев А.
Scratch и Arduino для юных
программистов и конструкторов
176 с., ISBN 978-5-94157-988-4
Книга написана на основе опыта работы с детьми 3 -7 классов и посвящена
созданию творческих проектов для юных программистов и конструкторов. На
примерах разработки простых компьютерных игр продемонстрированы ба­
зовые приемы визуального программирования в среде Scratch. Рассмотрено
применение плат Arduino, плат расширения и различных внешних датчиков
в детских конструкторских проектах. Даны основы визуального программи­
рования этих устройств в среде mBIock и креативного программирования пу­
тем написания интерактивных компьютерных игр, в которых управление пер­
сонажами осуществляется посредством Arduino. Также дети освоят методы
создания автономных «умны х вещей», работающ их под управлением Arduino
без подключения к компьютеру.
Электронный архив на сайте издательства содержит дополнительные материа­
лы и листинги всех программ.
В и н н и ц к и й Ю рий А н а то л ь е в и ч , кандидат педагогических наук, преподава­
тель информатики, неоднократный победитель проф ессиональных конкурсов,
автор книг и статей по робототехнике и конструированию, автор-разработчик
более 200 электронных ресурсов Единой коллекции циф ровых образователь­
ных ресурсов school-collection.edu.ru.
Г р и го р ь е в А л е к с а н д р Т и хо н о в и ч, психолог, преподаватель робототехники
и конструирования, призер международных соревнований по робототехнике,
автор ряда статей по робототехнике, конструированию и использованию новых
технологий в образовании.
Рудько М.
w w w .b h v.ru
Отдел о птовы х поставок:
E-mail: opt@bhv.spb.su
Раскрась свое настроение.
Цирк
64 с., ISBN 978-5-9775-3731-5
«И я боюсь стать таким, как взрослые, которым ничто не интересно, кроме
цифр. Еще и потому я купил ящ ик с красками и цветные карандаши».
Маленький принц. Антуан де Сент-Экзюпери
Перед вами раскраска для взрослых, которые все еще любят красивый и вол­
шебный мир цирка. На страницах этого альбома гуттаперчевые гимнастки ле­
тают на трапециях, цирковые фургоны приоткрывают свои двери, из-за кулис
выглядывают недобрые клоуны, красивые гадалки раскидывают на столе кар­
ты. Вам остается только взять карандаши и окунуться в веселье.
Бахчина А.
Раскрась свое настроение
80 с., ISBN 978-5-9775-3652-3
Многие, разговаривая по телефону или беседуя, чертят орнаменты. Не случай­
но. Это успокаивает. Но мало кто из нас умеет рисовать. Получается неловко,
и мы с досадой комкаем листок. А вот раскрасить орнамент проф ессиональ­
ного художника, самому подобрать палитру цветов и увидеть, как на кончике
карандаша рождается настоящая картина, — это вдохновляет и поднимает
настроение.