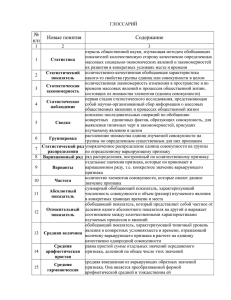
Организация охраны здоровья, программноцелевое планирование, медицинская статистика Занятие 7. «Цели, задачи, теоретические основы медицинской статистики» Этапы статистического исследования: I ЭТАП – составление программы и плана статистического исследования. II ЭТАП – организация и проведение сбора необходимых данных, предусмотренных программой исследования. III ЭТАП – осуществление обработки собранных данных (контроль – проверка полноты и качества собранного материала, группировка, шифровка, сводка в статистические таблицы, вычисление статистических показателей). IV ЭТАП – выводы и предложения на основе анализа полученных результатов исследования. Относительные величины В повседневной практической деятельности врач, как правило, получает любую информацию в абсолютных числах. Абсолютные величины несут важную информацию о размере того или иного явления и могут быть использованы в анализе, в том числе и в сравнительном. Однако они часто не отвечают на все поставленные вопросы. Так, например, врачу интересны сведения о здоровье обслуживаемого населения (показатели заболеваемости и др.), а у него есть информация только о числе зарегистрированных заболеваний (абсолютные числа), которые «заболеваемость» не характеризует. Для более углубленного анализа общественного здоровья и деятельности учреждений здравоохранения, а также деятельности медицинского работника используются обобщающие показатели, называемые относительными величинами. Различают 4 вида относительных величин: 1. Экстенсивные 2. Интенсивные 3. Соотношения 4. Наглядности Экстенсивный показатель – это показатель удельного веса, доли части в целой совокупности, показатель распределения совокупности на составляющие ее части, т.е. показатель структуры. Способ получения экстенсивной величины выглядит следующим образом: часть совокупности (явления или среды) х 100% вся совокупность (явление или среда) Экстенсивный показатель отвечает на вопрос, сколько процентов приходится на каждую конкретную часть совокупности. В зависимости от того, что характеризуют экстенсивные показатели, их называют: • показатели удельного веса части в целом, например, удельный вес гриппа среди всех заболеваний • показатели распределения или структуры (распределение всей совокупности зарегистрированных врачом заболеваний за год на отдельные заболевания). Пример расчета экстенсивных показателей: В районе А. в текущем году было зарегистрировано 500 случаев инфекционных заболеваний, из них: эпидемического гепатита – 60 случаев; кори – 100 случаев; прочих инфекционных заболеваний – 340 случаев. Задание: определить структуру инфекционных заболеваний. Решение: вся совокупность – 500 случаев инфекционных заболеваний принимается за 100%, составные части определяются как искомые. Удельный вес случаев эпидемического гепатита составит: 60 100% 12% 500 Аналогично рассчитывается удельный вес других заболеваний. Вывод: в структуре инфекционных заболеваний доля эпидемического гепатита составила 12%, кори – 20%, прочих инфекционных заболеваний – 68%. Интенсивный показатель – показатель частоты, уровня, распространенности процессов, явлений, совершающихся в определенной среде. Он показывает, как часто встречается изучаемое явление в среде, которая его продуцирует (заболеваемость, смертность, рождаемость и т.д.). Интенсивные показатели используются как для сравнения, сопоставления динамики частоты изучаемого явления во времени, так и для сравнения, сопоставления частоты этого же явления в один и тот же промежуток времени, но в различных учреждениях, на различных территориях и т.д. Способ получения интенсивного показателя выглядит следующим образом: явление х 100 (1000 и т.д.) среда Пример расчета интенсивных показателей: В городе проживает 120 000 человек (среда). В предыдущем году родилось 1080 детей (явление). Задание: определить показатель рождаемости (рассчитывается на 1000 населения). Решение: рождаемость = 1080 1000 9%0 120000 Вывод: рождаемость в городе составила 9%0. Показатель соотношения характеризует соотношение между двумя не связанными между собой совокупностями (обеспеченность населения койками, врачами, дошкольными учреждениями, соотношение родов и абортов, соотношение врачей и медицинских сестер и др.). Для получения этого показателя нужны две совокупности (№1 и №2). Абсолютная величина, характеризующая одну совокупность, делится на абсолютную величину, характеризующую другую, с ней не связанную совокупность и умножается на множитель (100, 1000, 10000 и т.д.): совокупность №1 х 10 000 совокупность №2 Пример расчета показателя соотношения: В городе 120 000 населения, общее число терапевтических коек – 300. Задание: требуется рассчитать обеспеченность населения терапевтическими койками. Решение: число коек – совокупность №1, численность населения – совокупность №2. показатель соотношения = 300 10000 25 120000 Вывод: на 10 000 населения в городе приходится 25 терапевтических коек, или обеспеченность населения города терапевтическими койками равна 25 коек на 10000 населения. Показатель наглядности применяется для анализа однородных чисел и используется, когда необходимо «уйти» от показа истинных величин (абсолютных чисел, относительных и средних величин). Как правило, эти величины представлены в динамике. Для вычисления показателей наглядности одна из сравниваемых величин принимается за 100% (обычно это исходная величина), а остальные рассчитываются в процентном отношении к ней. Примечание: особенно их целесообразно использовать, когда исследователь проводит сравнительный анализ одних и тех же показателей, но в разное время или на разных территориях. Пример расчета показателя наглядности: Задание: рассчитать показатели наглядности для уровней госпитализации в больничные учреждения города Н. в динамике за 5 лет наблюдения (см. таблицу). Таблица Уровень госпитализации в больничные учреждения в городах Н. и К. за 5 лет (на 100 человек населения) Годы 1 2 3 4 5 Уровень госпитализации в городе Н. 24,4 22,8 21,2 20,5 20,7 Показатель наглядности 100% Решение: снижение больных, поступивших в стационары, будет нагляднее, если приравнять показатель исходного уровня госпитализации городе Н. (1 год – 24,4) к 100%, а остальные показатели пересчитать в процентах по отношению к нему. 24,4 – 100% 22,8 – Х Х 22 ,8 100 93,44 % (показатель наглядности для 2-го года) 24 ,4 24,4 – 100% 21,2 – Х Х 21,2 100 86 ,9% (показатель наглядности для 3-го года) 24 ,4 24,4 – 100% 20,5 – Х Х 20 ,5 100 84 % (показатель наглядности для 4-го года) 24 ,4 24,4 – 100% 20,7 – Х Х 20 ,7 100 84 ,8%(показатель наглядности для 5-го года) 24 ,4 Вывод: в динамике за 5 лет наблюдения уровень госпитализации больных в городе Н. снижается. Наиболее часто встречающиеся ошибки в применении относительных величин: Ошибка 1. Когда исследователь сравнивает интенсивные показатели, характеризующие одно явление за периоды наблюдения, не равные по длительности. ВНИМАНИЕ: сравнивать интенсивные показатели можно только за равные промежутки времени (например, уровень травматизма за зимние месяцы предыдущего года сравнивается с уровнем травматизма за аналогичный период изучаемого года). Ошибка 2. Когда при сравнении полученных показателей за несколько месяцев делается заключение о тенденциях к снижению или повышению уровня данного явления. ВНИМАНИЕ: выводы о динамике явления можно делать только по результатам в целом за год при сравнении с уровнями изучаемого явления за несколько предыдущих лет. Ошибка 3. Когда для характеристики какого-либо явления применяется экстенсивный показатель вместо интенсивного. ВНИМАНИЕ: при анализе экстенсивных показателей следует помнить, что они характеризуют состав только данной конкретной совокупности (в нашем приведенном примере в данный момент больше было умерших доношенных детей, в то же время и абсолютное число родившихся доношенными было больше). Пример: В родильном доме из 22 умерших за изучаемый год 14 детей были доношенными, 8 – недоношенными, что составило 63% и 37% соответственно (см. таблицу). Исследователем был сделан неправильный вывод о том, что смертность доношенных детей выше, чем недоношенных. Для того чтобы сделать правильный вывод о сравнении смертности, новорожденных среди доношенных и недоношенных детей, необходимо рассчитать интенсивные показатели: частоту смертности среди всех родившихся доношенными (365 детей) и отдельно – частоту смертности среди всех родившихся недоношенными (52 ребенка). Рассчитанные интенсивные показатели на 100 родившихся составили: 14 100 4 365 8 100 15,4 52 (среди доношенных) (среди недоношенных) Число умерших (абс.) Экстенсивный показатель (в %) Число родившихся (абс.) Интенсивный показатель смертности (на 100 родившихся) Всего: 22 100 417 5,2 доношенные недоношенные 14 63 365 4 8 37 52 15,4 СРЕДНИЕ ВЕЛИЧИНЫ И КРИТЕРИИ РАЗНООБРАЗИЯ ВАРИАЦИОННОГО РЯДА Введение: При изучении общественного здоровья (например, показателей физического развития), анализе деятельности учреждений здравоохранения за год (длительность пребывания больных на койке и др.), оценке работы медицинского персонала (нагрузка врача на приеме и др.) часто возникает необходимость получить представление о размерах изучаемого признака в совокупности для выявления его основной закономерности. Оценить размер признака в совокупности, изменяющегося по своей величине, позволяет лишь его обобщающая характеристика, называемая средней величиной. Для более детального анализа изучаемой совокупности по какому-либо признаку помимо средней величины необходимо также вычислить критерии разнообразия признака, которые позволяют оценить, насколько типична для данной совокупности ее обобщающая характеристика. Вариационный ряд – это ряд числовых значений какого-либо признака, отличающихся по величине и расположенных в определенном порядке. Вариационный ряд является одним из типов распределения признака в статистической совокупности и служит для вычисления средних величин. Назначение вариационного ряда: вариационный ряд используется для определения средней величины (М) и критериев разнообразия признака, подлежащего изучению ( , CV ). Характеристиками вариационного ряда являются: варианта (v) – числовое значение изучаемого признака; частота (р), с которой встречается каждая варианта (число повторений варианты в вариационном ряду); общее число наблюдений, сумма всех частот ( n р ), – знак суммы. vmax иvmin – крайние варианты, ограничивающие вариационный ряд (лимиты ряда) Am – амплитуда ряда (разность между максимальной и минимальной вариантами) Виды вариационных рядов: По частоте встречаемости варианты: простой – ряд, в котором каждая варианта встречается по одному разу (р=1); взвешенный – варианта встречается два и более раз. По объединению вариант в группы: несгруппированный – варианты не объединены в группы; сгруппированный – ряд, в котором где варианты объединяются в группы с указанием частоты встречаемости вариант, входящих в данную группу. Несгруппированный вариационный ряд составляют обычно при малом числе наблюдений (n<30), а сгруппированный ряд – при большом числе наблюдений (n>30). Простой вариационный ряд: Вес в кг v Частота признака p 16 1 17 1 18 1 19 1 20 1 21 1 22 1 23 1 24 1 25 1 26 1 27 1 28 1 Не сгруппированный (взвешенный) вариационный ряд: Вес в кг v Частота признака p 16 1 17 2 18 4 19 6 20 6 21 8 22 10 23 19 24 7 25 7 26 5 Сгруппированный вариационный ряд: Рост в см v Частота признака p 127 – 129 6 130 – 132 16 133 – 135 27 136 – 138 54 139 – 141 57 142 – 144 42 145 – 147 12 При составлении сгруппированного вариационного ряда необходимо выделить интервал (i), показывающий число вариант, объединенных в одну группу. v max v min i r r – число групп Правильно составленный сгруппированный ряд должен отвечать следующим требованиям: общее число выделенных групп должно быть не менее 7 (иначе средняя арифметическая будет неточной) и не более 15, т. к. ряд будет громоздким; каждая новая последующая группа должна начинаться с новой последующей варианты, т.е. одна и та же варианта не должна встречаться в 2-х смежных группах; интервал должен быть одинаковым в каждой группе, т. е., в каждую группу должно входить одинаковое число вариант; каждая группа в сгруппированном вариационном ряду должна иметь начальную и конечную варианты. Под средней арифметической величиной (М) понимается обобщающая характеристика размера изучаемого признака в статистической совокупности. Она позволяет одним числом количественно охарактеризовать качественно однородную совокупность. Применение средних величин: для оценки состояния здоровья – например, параметров физического развития (средний рост, средний вес, средний объем жизненной емкости легких и др.), соматических показателей (средний уровень сахара в крови, средний пульс, средняя СОЭ и др.); для оценки организации медицинских организаций, а также деятельности отдельных врачей и других медицинских работников (средняя длительность пребывания больного на койке, среднее число посещений на 1 ч приема в поликлинике и др.). Существуют разные способы определения средних величин в вариационных рядах: Наиболее просто и быстро можно определить моду (Мо) и медиану (Ме) в не сгруппированных вариационных рядах. Мода (Мо) – это средняя величина, которая соответствует варианте, имеющей наибольшую частоту. Медиана (Ме) – средняя величина, которая делит вариационный ряд на две равные части, занимающая в ранжированном ряду среднее место. В ряду, содержащем нечетное число наблюдений, медианой будет варианта, располагающаяся в середине ряда. В четном ряду медиана равна полусумме двух срединно-расположенных вариант. Способы вычисления средней арифметической: Простая средняя арифметическая: v M n вычисляется в тех случаях, когда варианты встречаются с одинаковой частотой и в совокупности, где n<30 (n – число наблюдений). Взвешенная средняя арифметическая: vp M n вычисляется в тех случаях, когда варианты встречаются с неодинаковой частотой и в совокупности, где n>30. Средняя арифметическая по способу моментов может быть вычислена в тех случаях, когда варианты представлены большими числами и имеется число наблюдений, выраженное сотнями или тысячами случаев: аp M A n A – условная средняя (чаще мода - Мо ); а – отклонение каждой варианты от условной средней. р – частота встречаемости признака; n – число наблюдений. Этапы вычисления средней арифметической по способу моментов в простом не сгруппированном вариационном ряду 1. 2. Выбрать условную среднюю А, за которую можно принять любую варианту, но лучше моду (Мо). Определить условные отклонения (а) каждой варианты от условной средней величины по формуле: a v A 3. 4. 5. Умножить отклонения на соответствующие частоты (ap) для каждой варианты. Суммировать полученные произведения ( ap). Рассчитать среднюю арифметическую по формуле: ap M A n Средняя арифметическая величина по способу моментов для сгруппированного вариационного ряда определяется по формуле: а p M Ai 1 n i – интервал. Этапы вычисления средней арифметической в сгруппированном вариационном ряду 1. 2. Определить количество групп в вариационном ряду по таблице. Определить величину интервала (i) между группами (разность между максимальными и минимальными значением вариант делят на число групп): i 3. 4. 5. v m ax v m in r Определить средину интервала. Выбрать условную среднюю арифметическую A (обычно Мо). Рассчитать отклонения для каждой группы вариант по формуле: a v A 6. Полученное отклонение сократить на величину интервала, т.е. рассчитать сокращенные отклонения: a a1 i 7. Умножить сокращенные отклонения на соответствующие частоты ( a p ). 1 8. Определить сумму полученных произведений а р 1 9. Рассчитать среднюю арифметическую по формуле: ap M Ai 1 n Критерии разнообразия признака в вариационном ряду: Характеризующие границы совокупности: Лимит: Lim vmax vmin Амплитуда или размах: Am vmax vmin Характеризующие внутреннюю структуру совокупности: среднее квадратичное отклонение ( - сигма) – мера колеблемости (вариабельности ряда), выражается в тех же единицах, что и варианты ряда. если n 30 , среднее квадратичное отклонение вычисляется по формуле: 2 а – отклонение от средней величины; р – частоты; n – число наблюдений. a p n если n 30, среднее квадратичное отклонение вычисляется по формуле: 2 a n 1 p Применение среднеквадратического отклонения: 1) для реконструкции вариационного ряда, т.е. восстановления его частотной характеристики на основе правила «трех сигм». В интервале М±3σ находится 99,7% всех вариант ряда, в интервале М±2σ – 95,5% и в интервале М±1σ – 68,3% вариант ряда; Для оценки единичной варианты также можно использовать правило М+3σ, т. е. если единичная варианта лежит в пределах: М+σ – это норма (нормальный рост, вес); М+2σ – рост или масса выше средней нормы; М+3σ – очень высокий или очень низкий рост. 2) для расчета коэффициента вариации; 3) для расчета средней ошибки средней арифметической величины. Коэффициент вариации CV – процентное отношение среднеквадратического отклонения к среднеарифметической величине, вычисляется по формуле: С V M 100 % Применение коэффициента вариации: для оценки разнообразия каждого конкретного вариационного ряда и, соответственно, суждения о типичности отдельной средней (т.е, ее способности быть полноценной обобщающей характеристикой данного ряда). при коэффициенте вариации <10% разнообразие ряда считается слабым, при коэффициенте вариации от 10% до 20% – средним, при коэффициенте вариации >20% – сильным. Сильное разнообразие ряда свидетельствует о малой представительности (типичности) соответствующей средней величины и, следовательно, о нецелесообразности ее использования в практических целях. Средняя ошибка средней арифметической величины: при n > 30 при n<30 m n m n 1 Среднее арифметическое отклонение (средняя ошибка средней арифметической) необходимы для оценки точности выборочного материала.