Оценка вариативности
реклама

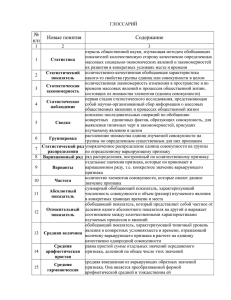
Оценка вариативности Л.Е.Федорова Признак • Признак это свойство, проявлением которого один предмет отличается от другого. • Характерным свойством признака является варьирование при переходе от одной единицы наблюдения к другой Варьирование признака • Вариация – колебания одного признака в массе однородных членов статистической совокупности • Варианта – числовые значения варьирующего признака Причины варьирования признаков: 1. Естественные колебания признака (например, суточное изменение температуры тела) 2. Погрешности (ошибки) измерения • Технические • Личные • Случайные Признаки 1. Качественные (атрибутивные) – нельзя измерить (например, цвет глаз) 2. Количественные – можно измерить • Мерные (метрические) - могут быть дробными (например, рост, вес) • Счетные (меристические) – не могут быть дробными (например, количество детей) Способы группировки первичных данных • Статистические таблицы (простые, сложные) • Статистические ряды (атрибутивные, вариационные, ряды динамики и регрессии, а так же ряды ранжированных значений и ряды накопления частот – производные вариационных рядов) Вариационный ряд • Это двойной ряд чисел, показывающий, каким образом числовые значения признака связаны с их повторяемостью в данной статистической совокупности • Ранжирование – расположение членов ряда в возрастающем или убывающем порядке Ма Ма сс ар еб сс ар еб 3,4 3,3 3,2 3 3,1 9 8 7 6 5 4 3 2 1 0 2,9 Полигон распределения частот 2,8 2,7 ен ка ,к г 2,5 2,6 3,4 3,2 3,3 3 3,1 ен ка ,к г 2,5 2,6 2,7 2,8 2,9 Графики вариационных рядов Гистограмма 9 8 7 6 5 4 3 2 1 0 Средняя арифметическая • Этот показатель является центром распределения, вокруг которого группируются все варианты статистической совокупности. • Она может быть простой и взвешенной Средняя арифметическая • Простая: X=(x1+x2+x3+…+xn)/n = 1/nΣxi • Взвешенная: X= 1/nΣxifi Медиана • Средняя, относительно которой ряд распределения делится на две равные части – в обе стороны от медианы располагается одинаковое число вариант: • 12 14 16 18 20 22 24 26 28; Ме=20 • 6 8 10 12 14 16 18 20 22 24; Ме = (14+16)/2 = 15 Мода • Это величина, наиболее часто встречающаяся в данной совокупности: xi 5 6 7 8 9 10 11 12 fi 2 1 4 7 6 5 4 3 Mo = 8 (встречается 7 раз) Размах вариации • R – это разность между максимальной и минимальной вариантами совокупности R = xmax – xmin • Среднее линейное отклонение – сумма отклонений вариант от их средней, взятая без учета знаков и отнесенная к числу наблюдений dср = Σ|xi - x |/n Дисперсия • Показатель, построенный на квадратах отклонений вариант от средней s2 = Σ(xi - x)2/n s2 = Σfi(xi - x)2/n Среднее квадратическое отклонение • Показатель, представляющий корень квадратный из дисперсии sx = Σ(xi - xс)2/(n-1) Спасибо за внимание!