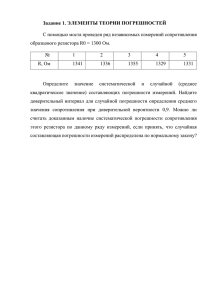
МЕТРОЛОГИЯ
ЛЕКЦИИ 2018/2019 учебный год ФЭА II курс
АВТОРЫ
АЛЕКСАНДРОВА А.П. ГРУППА 7493
БЕЛОВЕНЦОВА А.А. ГРУППА 7492
ГОГАН В.В. ГРУППА 7492
НАУЧНЫЙ РУКОВОДИТЕЛЬ
БИШАРД Е.Г.
РЕДАКТОРЫ
МИГРАНОВ Р.М. ГРУППА 7493
СТРОГАЛЕВ П.Н. ГРУППА 7493
Содержание
1. Предмет и задачи курса ........................................................................................................................................... 3
2. Общее представление об измерениях. Понятия об измерении физической величины. Структурная схема
процесса измерения ...................................................................................................................................................... 4
3. Процесс измерений с точки зрения теории вероятности .................................................................................. 7
4. Классификация измерений ..................................................................................................................................... 8
5. Классификация средств измерений..................................................................................................................... 12
6. Классификация методов измерений.................................................................................................................... 18
7. Нулевой метод на примере потенциометра постоянного тока....................................................................... 23
8. Нулевой метод на примере моста постоянного тока. Мосты равновесные и неравновесные. ................ 24
9. Потенциометр переменного тока ......................................................................................................................... 26
10. Мосты переменного тока ..................................................................................................................................... 27
11. Дифференциальный метод измерения на примерах ...................................................................................... 29
12. Структурные схемы средств измерений прямого преобразования ............................................................ 30
13. Структурные схемы средств измерений компенсационного преобразования с астатической
характеристикой ......................................................................................................................................................... 32
14. Структурные схемы средств измерений компенсационного преобразования со статической
характеристикой ......................................................................................................................................................... 34
15. Автоматический мост для измерения сопротивлений .................................................................................. 37
16. Электронный веберметр ...................................................................................................................................... 38
17. Структурные схемы средств измерений с автоматической коррекцией ................................................... 41
18. Измерительне преобразователи. Классификация: по входным и выходным величинам...................... 43
19. Измерительные преобразователи. Первичные, вторичные. Генераторные, параметрические............ 47
20. Преобразователи с унифицированным выходным сигналом ...................................................................... 48
21. Аналого-цифровые преобразователи. Методы построения АЦП. Квантование. Погрешность
дискретности. ............................................................................................................................................................... 50
22. Классификация измерительных приборов с краткой характеристикой (показывающие,
регистирующие, регулирующие, электромеханические, электронные, цифровые, аналого-дискретные)
........................................................................................................................................................................................ 54
23. Типы отсчетных устройств в измирительных приборах .............................................................................. 59
24. Метрологические характеристики средств измерения в статическом режиме ........................................ 60
25. Динамический режим. Динамические характеристики средств измерений ............................................. 64
26. Нормирование метрологических средств измерений. ................................................................................... 70
27. Нормирование погрешности средств измерений. Класс точности .................................................................. 70
28. Общие сведения о погрешности измерений. Причины появления погрешностей. Классификация ... 73
29. Погрешности систематические и случайные. Описание случайных погрешностей. Понятие
доверительного интервала погрешности ............................................................................................................... 75
30. Идея суммирования погрешности ..................................................................................................................... 79
31. Получение результата измерений при обработке ряда прямых наблюдений........................................... 80
32. Общие сведения об электромеханических приборах. Структурная схема. Моменты, действующие в
приборе. Классификация измерительных механизмов и приборов на их основе кратко ............................ 82
2
33. Магнитоэлектрические приборы. Принцип действия м/э измерительного механизма с механическим
противодействующим моментом ............................................................................................................................. 87
34. Магнитоэлектрические приборы. Принцип действия м/э измерительного механизма с
электрическим противодействующим моментом ................................................................................................ 89
35. Магнитоэлектрические амперметры ................................................................................................................ 90
36. Магнитоэлектрические вольтметры................................................................................................................. 95
37. Индукционные измерительные механизмы .................................................................................................... 96
38. Магнитоэлектрические омметры ...................................................................................................................... 97
39. Индукционный счетчик энергии ....................................................................................................................... 98
40. Электродинамические измерительные механизмы ..................................................................................... 100
41. Электродинамические амперметры ................................................................................................................ 102
42. Электродинамические вольтметры ................................................................................................................ 103
43. Электродинамические ваттметры ................................................................................................................... 104
44. Общие сведения об электронных приборах ................................................................................................... 105
45. Электронный комбинированный вольтметр ................................................................................................ 107
46. Электронные вольтметры постоянного тока с преобразованием спектра ............................................. 109
48. Электронные вольтметры переменного тока ............................................................................................... 112
49. Селективные вольтметры ................................................................................................................................. 115
50. Детекторы электронных вольтметров............................................................................................................ 117
51. Электронный однолучевой осциллограф с электростатическим управлением луча. Упрощенная
структурная схема .................................................................................................................................................... 120
52. Узлы электронного осциллографа и требования к ним .............................................................................. 126
53. Канал вертикального отклонения осциллографа ........................................................................................ 126
54. Канал горизонтального отклонения осциллографа ..................................................................................... 127
55. Понятие о развертке. Непрерывная и ждущая развертка .......................................................................... 128
56. Понятие о синхронизации. Амплитуда синхронизации и частота ............................................................ 131
57. Общие сведения о цифровых (ЦИП) приборах. Методы построения АЦП. Погрешности ЦИП ........ 132
58. Вольтметр на принципе считывания.............................................................................................................. 137
59. Времяимпульсный цифровой вольтметр ....................................................................................................... 138
Приложение................................................................................................................................................................ 141
3
1. Предмет и задачи курса
Пусть мы имеем сколь угодно сложный объект.
Зададимся целью получить о его свойствах достоверную информацию. Что такое
«достоверная» информация? Это такая информация, которая является несомненно
верной для человека, её, эту информацию, воспринимающего. То есть информация
может являться достоверной или недостоверной не «вообще», а только для человека
получающего эту информацию. В нашем предмете, метрологии, вероятность
достоверности информации обычно составляет что-то около 0.9973 и вплоть до 0.999.
Тело
Физ. величина
Явления
Процесс
Совокупность физ.
величин
Система
Сколь угодно сложный
объект измерения
Цель-получение
достоверной
информации о
свойствах объекта.
Что я о тебе знаю?
Для единичных
параметров(+)
Чёрный ящик(ничего не
знаю)
Априорная(исходная)
Для комплексных
параметров(+)
Средства измерений –
чем измеряют (+)
Информационно
измерительные
системы(ИИС)(+)
Измерительно
вычислительные
комплексы(ИВС)(+)
Чтобы получить информацию,
нужно поставить
измерительный эксперимент
Методы измерения(+)
Для того, чтобы
поставить измер.
эксперимент нужно
составить его план (-)
Обработка результатов
измерений(+)
┌Без априорной информации измерение невозможно. Априорной измерительной
информацией является вся сумма знаний об измеряемом объекте и условиях
проведения измерений, которой располагают до начала измерений. Действительно,
если об исследуемом объекте мы ничего не знаем, то не можем начать измерение;
неизвестно, что измерять, каким образом и каким средством измерений измерять и с
какими величинами сравнивать. Априори – знание, полученное до опыта.┘
Метрология – наука о мерах; методах и средствах измерения величин, об
обеспечении единства измерений и точностных характеристиках (способах
достижения требуемой точности).
┌ Предметом метрологии является извлечение количественной информации о
свойствах объектов с заданной точностью и достоверностью (являются методы и
средства измерений, а также методы и средства достижения и обеспечения
установленной точности).
Средством метрологии является совокупность измерений и
метрологических стандартов, обеспечивающих требуемую точность.┘
Единство измерений – состояние измерений, при котором их результаты выражены в
узаконенных единицах, а погрешности известны с определённой вероятностью.
┌(погрешность не выходит за установленные рамки). То есть, здесь нет и быть не
может никакой «неопределённости»: заранее известны единицы измерения величины,
и сама величина (число) должна укладываться в определённые рамки (читай – в
погрешность).┘
4
Узаконенные единицы: СИ, SgSM
Метрология
научная - база измерительной техники,
занимающаяся изучением проблем
измерения в целом и образующих
измерение элементов: средств
измерений, физических величин и их
единиц, методов и методик измерений,
результатов и погрешностей измерений
законодательная - разрабатывает и
внедряет нормы и правила выполнения
измерений.
Существет система: Гос. система
обеспечения единства измерений
(стандарт ГСИ)
Стандартизация – установление и применение правил, с целью упорядочения
деятельности в определённой области на пользу, при участии всех заинтересованных
сторон.
Сертификация – деятельность на подтверждение качества продукции.
Квалиметрия – наука об оценке качества. ┌ То есть изделие не просто оценивается,
как «хорошее / плохое» или «работающее / неработающее», а оценка производится
числом.
┘
2. Общее представление об измерениях. Понятия об измерении физической
величины. Структурная схема процесса измерения
Измерить физическую величину - значит найти её значение опытным путём с
помощью технических средств (физическую величину ищем в узаконенных
единицах(СИ)).
Физическая величина – это свойство, общее или присущее в качественном
отношении многим объектам и предметам, но индивидуально в количественном.
Физические величины:
• Аналоговые (непрерывные);
• Дискретные (квантованные, известные только на определённом интервале);
• Квазидетерминированные (величины, у которых известен закон распределения
во времени, но не их параметры);
• Случайные (меняющиеся случайным образом);
Различают:
• Истинное значение измеряемой величины – значение, которое абсолютным,
истинным образом характеризует данную величину.
• Действительное значение – значение, которое определяется экспериментально
и настолько близко приближенно к истинному, что его можно принять за
истинное.
5
Пример:
x-измеряемая величина;
х =I
I=
𝑈𝑈
𝑅𝑅н +𝑟𝑟𝑖𝑖
Ставим эксперимент:
А
1
𝐼𝐼 ∗ =
𝑈𝑈
𝑅𝑅н +𝑟𝑟𝑖𝑖 +𝑅𝑅𝐴𝐴
2
;
3
4
5
I*=3А –
действительное
значение
Когда будет 𝐼𝐼=𝐼𝐼 ∗ -?, только в случае 𝑅𝑅𝐴𝐴 =0;
Но такого в жизни сложно, невозможно достичь, так как приборы для своей работы
должны потреблять энергию, следовательно 𝐼𝐼 ∗ ≠ 𝐼𝐼
┌Таким образом, искомый ток будет найден тем точнее, чем менее будет
сопротивление выбранного нами амперметра. В идеале оно (сопротивление
амперметра), как известно, должно стремиться к нулю.┘
Точность измерений – качество измерений, отражающее близость результатов
измерений к истинному значению измеряемой величины (т.е. близости к нулю
погрешности результата измерений).
Погрешность результата измерений (мера точности) – разность между измеренным
и истинным значением измеряемой величины. ∆x=∆𝑥𝑥измер -∆𝑥𝑥ист = 𝑥𝑥измер − 𝑥𝑥действ
Погрешность - величина, обратная точности.
Пример:
а) RA=10 Ом
б) RA=1 Ом
в) RA=0,5 Ом !!!
Уравнения измерений:
x=a[q];
q - единица измерений;
х-измеряемая величина;
а-число;
При измерении получаем ряд измерений. Для получения
результата, надо проводить математическую обработку.
6
Пример:
𝑈𝑈вых = 𝑈𝑈а + sin(𝜔𝜔𝜔𝜔)
Генератор синусоидальных
напряжений
Считаем, что сигналы чисто синусоидальны,
следовательно, достаточно посмотреть амплитуду:
а) Амплитудный вольтметр
Амплитудный вольтметр, соответственно измеряет
амплитудное значение
Показания: ux=150В
б) Вольтметр показывает действующее значение
Показания: ux=150В, значит амплитудное значение 150√2
Содержит гармоники:
А1=f1
А2=f2
А3=f3
┌ Первая гармоника f1=1 кГц; вторая f2=2 кГц;
f3=3 кГц …┘
┌Уравнения напряжения, содержащее эти
гармоники: u(t)=U0+U1√2cos(2πf1t+au1)+ U0+U2√2cos(2πf2t+au2)+….
Чистая синусоида
=
f (t ) Fm * cos(ω0t + α ) - тоже ПС, она содержит только 1
A1 = Fm
┘
гармонику (саму себя), т.е.:
Ф1 = α
Вводят такие понятия как:
Правильные измерения – качество измерений, у которых систематическая
погрешность близка к нулю, практически отсутствует или исключена.
Сходимость измерений – качество измерений, отражающее близость результатов
измерений друг к другу, выполненных в одинаковых условиях.
Воспроизводимость – качество измерений, отражающее близость результатов
измерений друг к другу, выполненных в различных условиях, в различное время,
различных местах, разными людьми.
7
Структурная схема процессов измерений
МОИ – множество объектов измерений.
ОИ – объект измерений.
Т - тезаурус – технический словарь моделей, построенный на определенной
структурной схеме, где сведения, собраны и систематизированы.
СО – схема опознавания.
АИ - алгоритм измерения - строгое предписание процедур, ранее выбранных нами,
которые должны выполняться.
СИ – средство измерений.
Р – результат.
Такая схема очень встраивается в систему принятия решений.
3. Процесс измерений с точки зрения теории вероятности
Информация уменьшает долю неопределённости наших знаний о чём-то.
В физике неопределённость связана с энтропией.
┌Энтропия – мера неопределённости ситуации, или в более широком смысле – мера
неопределённости вселенной. ┘
∞
Математически энтропия – это функционал вида H = -∫−∞ 𝑝𝑝(𝑥𝑥) ln 𝑝𝑝(𝑥𝑥) 𝑑𝑑𝑑𝑑
p(x) – плотность распределения (иногда w(x)).
Пример:
А) До измерения
I = x;
Априори знаем
I = 0÷5 A; 𝑥𝑥𝑚𝑚𝑚𝑚𝑚𝑚 ÷ 𝑥𝑥𝑚𝑚𝑚𝑚𝑚𝑚
┌ Величина X может с равным успехом принять любое значение
𝑋𝑋𝑀𝑀𝑀𝑀𝑀𝑀 < 𝑋𝑋 < 𝑋𝑋𝑀𝑀𝑀𝑀𝑀𝑀 из интервала от «икс-минимум» до «икс-максимум». Тогда,
плотность распределения вероятности: ┘
Равномерный закон
8
В этом случае
1
p(x) =
;
𝑥𝑥𝑚𝑚𝑚𝑚𝑚𝑚 −𝑥𝑥𝑚𝑚𝑚𝑚𝑚𝑚
𝑥𝑥𝑚𝑚𝑚𝑚𝑚𝑚
1
1
H = -∫𝑥𝑥
ln
𝑑𝑑𝑑𝑑=ln(𝑥𝑥𝑚𝑚𝑚𝑚𝑚𝑚 −
𝑥𝑥𝑚𝑚𝑚𝑚𝑚𝑚 −𝑥𝑥𝑚𝑚𝑚𝑚𝑚𝑚
𝑚𝑚𝑚𝑚𝑚𝑚 𝑥𝑥𝑚𝑚𝑚𝑚𝑚𝑚 −𝑥𝑥𝑚𝑚𝑚𝑚𝑚𝑚
𝑥𝑥𝑚𝑚𝑚𝑚𝑚𝑚 )
Б) После измерения
┌Например, показания прибора
xп=3А┘
Неопределённость сократилась, но осталась.
∆- погрешность.
𝑥𝑥 +∆ 1
1
Hу = -∫𝑥𝑥 п−∆
ln 𝑑𝑑𝑑𝑑=ln(2∆)
п
2∆
2∆
Количество информации: q= H(x) – Hу(x/xп) = ln
𝑥𝑥𝑚𝑚𝑚𝑚𝑚𝑚 −𝑥𝑥𝑚𝑚𝑚𝑚𝑚𝑚
𝑥𝑥𝑚𝑚𝑚𝑚𝑚𝑚 −𝑥𝑥𝑚𝑚𝑚𝑚𝑚𝑚
2∆
;
- число допустимых градаций (в цифровой технике).
4. Классификация измерений
1. По роду измеряемой величины
• Электрические (I, R, U, P …)
• Электрические измерения неэлектрической величины (давление, механический
момент и т.д.)
2∆
�⃗))
• магнитные измерения (существует единое электромагнитное поле(𝐸𝐸�⃗ , 𝐻𝐻
2. По удалению источника информации от объекта
• непосредственные
• дистанционные (телеизмерения). ┌Телеизмерение измерение на расстоянии средствами телемеханики физических величин, характ
еризующих состояниеконтролируемых объектов.┘
3.
По количеству измерений одной и той же измеряемой величины
• однократные, т.е. один раз померили результат, получили и поверили.
• многократные: в результате получаем ряд измерений, при обработке этого ряда
методами мат. статистики получаем результат.
Многократные измерения проводим, чтобы учесть случайную погрешность. Ведь
очевидно, чем больше раз измерим физическую величину, тем меньше «места»
останется для случайностей.
Примечание: из этого перечисленного выделяются статистические измерения.
4. По точности
• Эталонные (с высочайшей точностью)
• Технические (гарантируют определённую точность)
┌Вовсе неверным было бы считать технические измерения неточными. Они просто не могут называться
эталонными, так как не дают абсолютной точности, которая в технических измерениях и не требуется.
А требуется там только лишь гарантия определённой точности, за что технические измерения
отвечают.┘
5. По поведению измеренной величины во времени
9
• статические (полагаем измеряемую величину неизменной во времени)
• динамические (главный вопрос: как ведёт себя измеряемая величина во
времени?)
Примечание: не путать статические со статистическими
6. По способу снятия показаний
• непрерывные (показания можно снять в любой момент времени)
• дискретные
Дискретная случайная величина – та, значения которой известны только в
отдельно взятые моменты времени.
Пример 1: Непрерывные
Пример 2: Дискретные
┌У радистов это называется набор дискретных сообщений.┘
В зависимости от определённых условий можно по набору дискретных сигналов
восстановить ситуацию, как ведёт себя величина на интервале.
7. По методу измерений
• прямые
• косвенные
• совокупные
• совместные
1. Прямые измерения - измерение, при котором искомое значение физической
величины получают непосредственно в результате выполнения
измерительного эксперимента.
Измеряемая величина X измеряется непосредственно прибором.
Пример:
10
I=X=?
Величину измеряем непосредственно прибором, измеряющим ЭТУ, конкретную
величину (например ток – амперметром, сопротивление – омметром, вес – весами,
длину линейкой или метром и т.д.).
2. Косвенные измерения – определение искомого значения физической
величины на основании результатов прямых измерений других физических
величин, функционально связанных с искомой величиной.
, т.е. Q1 и Q2 связаны с X функцией, которая известна.
Пример:
Расчет мощности: P=?
1) Прямые измерения Pиз – прибор ваттметр.
2) Косвенные: измерить ток и напряжение и использвать формулу P=I*U
Пример
Естественно, по ЗТК, амперметр будет, в
данном случае, мерить не «чистый» ток
нагрузки, а ток нагрузки плюс ток
вольтметра, который хоть и мал (из-за его
большого сопротивления), а всё же имеет
место быть и портит общую картину
измерений.
I=IH+IB
I ≠ IH
По ЗНК для данного контура:
UB=UH+UA
UH ≠ U
И тут наблюдается ошибка.
А в целом, мощность тогда:
PH=IH*UH!!!!!
3. Совокупные - проводимые одновременно измерения нескольких
одноименных величин, при которых искомые значения величин определяют
путем решения системы уравнений, получаемых при измерениях этих величин в
различных сочетаниях. По сути, совокупные измерения – это одновременно
проводимые косвенные измерения. Потом решают данную систему уравнений:
11
𝑓𝑓(𝑥𝑥1 , 𝑥𝑥2 , … , 𝑄𝑄11 , 𝑄𝑄21 , … ) = 0
𝑓𝑓(𝑥𝑥1 , 𝑥𝑥2 , … , 𝑄𝑄12 , 𝑄𝑄22 , … ) = 0 Система уравнений,
………………………
⎨
⎩𝑓𝑓(𝑥𝑥1 , 𝑥𝑥2 , … , 𝑄𝑄1𝑛𝑛 , 𝑄𝑄2𝑛𝑛 , … ) = 0
где x1, x2, … - искомые величины; Q (i) 1, Q (i) 2, …, - значения искомой величины
Исходные данные: интересующие величины (x1, x2, …) находят из решения системы
уравнений, связывающих эти величины с измеряемыми величинами при их различных
сочетаниях.
Пример
В совокупных измерениях все величины должны
быть одной природы.
Магнитные потери: (на рис)
Для измерения Pм есть прибор.
Совокупные измерения связывают одноименные величины
Известно: (f -частота)
Рг = 𝑎𝑎 ∗ 𝑓𝑓 𝑃𝑃вт = 𝑏𝑏 ∗ 𝑓𝑓 2 => 𝑃𝑃𝑀𝑀 = 𝑎𝑎 ∗ 𝑓𝑓 + 𝑏𝑏 ∗ 𝑓𝑓 2
Пусть 𝑄𝑄1 = 𝑃𝑃𝑀𝑀 , 𝑄𝑄2 = 𝑓𝑓,
𝑥𝑥1 = 𝑃𝑃г , 𝑥𝑥2 = 𝑃𝑃вт
Опыт 1:
Опыт 2:
𝑓𝑓1 = 1 кГц
𝑓𝑓2 = 10 кГц
2
𝑃𝑃𝑀𝑀1 = 𝑎𝑎 ∗ 𝑓𝑓1 + 𝑏𝑏 ∗ 𝑓𝑓1 ,
𝑃𝑃𝑀𝑀2 = 𝑎𝑎 ∗ 𝑓𝑓2 + 𝑏𝑏 ∗ 𝑓𝑓22 .
𝑃𝑃 = 𝑎𝑎 ∗ 𝑓𝑓1 + 𝑏𝑏 ∗ 𝑓𝑓12
� 𝑀𝑀1
находим a и b
𝑃𝑃𝑀𝑀2 = 𝑎𝑎 ∗ 𝑓𝑓2 + 𝑏𝑏 ∗ 𝑓𝑓22
Расчет: 𝑃𝑃г = 𝑎𝑎 ∗ 𝑓𝑓; 𝑃𝑃вт = 𝑏𝑏 ∗ 𝑓𝑓 2
4. Совместные – проводимые одновременно измерения двух или нескольких
неодноименных величин для определения зависимости между ними.
Разновидность совокупных – совместные.
Это тоже самое, что совокупные, но только одна величина в этом случае
электрическая, а другая – нет.
Пример:
Есть резистор, и есть солнце, под воздействием коего
этот резистор греется.
Зависимость сопротивления от температуры такая Rt
= F(t).
Примем: 𝑅𝑅 = 𝑅𝑅0 + 𝛼𝛼 ∗ 𝑡𝑡 + 𝛽𝛽 ∗ 𝑡𝑡 2
Причем одна из величин в выражении электрическая
(сопротивление), а другая – неэлектрическая
(температура).
Измеряют сопротивление резистора при трех различных температурах, составляют
систему из трех уравнений и находят значения параметров R0, α и β.
Найти: 𝛼𝛼 и 𝛽𝛽
Опыт 1: t = 0
Опыт 2: t1
=>
𝑅𝑅0 𝛼𝛼 и 𝛽𝛽
Опыт 3: t2
Примечание:
Разница между совокупными и совместными измерениями заключается в том, что
совместные измерения проводятся одновременно для неодноимённых (разной
природы) величин с целью определения зависимостей между ними, а совокупные
⎧
12
измерения проводятся для нескольких одноимённых (одной природы) величин, с
целью их нахождения из системы уравнений.
5. Классификация средств измерений
1) Эталоны
2) Меры
3) Измерительные приборы
4) Измерительные преобразователи
5) Измерительные установки
6) Информационно-измерительные системы (ИИС)
7) Измерительно-вычислительные комплексы (ИВК)
8) Интеллектуальные средства
┌Средство измерения (СИ) – техническое средство, предназначенное для
измерений, имеющее нормированные метрологические характеристики,
воспроизводящее и (или) хранящее единицу физической величины, размер
которой принимают неизменным (в пределах установленной погрешности) в
течение известного интервала времени).┘
Эталоны
Эталоны – средства измерений, предназначенные для воспроизведения, хранения и
передачи единицы физической величины (в СИ).
Международное бюро мер и весов находится на севере Парижа. В Париже на
генеральной конференции по мерам и весам приняты новые определения кг, А, К,
моль. Эталоны будут основаны на квантовых эффектах.
Меры
Мера – средство измерений, предназначенное для воспроизводства и (или) хранения
физической величины одного и нескольких заданных размеров, значения которых
выражены в установленных единицах и известны с необходимой точность.
Мера воспроизводит величину определенного размера и передает другим приборам.
┌Гири. Образцовое сопротивление
Rобр = 100 Ω
В приведенном примере рассмотрена однозначная мера. Существуют и многозначные меры, скажем,
магазин сопротивлений, который воспроизводит любое сопротивление принадлежащее заданному
диапазону.
Набор мер — устройство, воспроизводящее несколько физических величин заданного размера┘
Измерительные приборы
Это средства для выработки сигнала измерительной информации в форме, доступной
для восприятия наблюдателем.
И шкалы, и указатели – различны для приборов, основанных на различных принципах.
13
Примечание: большинство шкал должны быть проградуированы в единицах
физической величины, но есть неградуированные шкалы – такие приборы требуют
дополнительной градуировки (в делениях).
Измерительные приборы делятся на несколько групп как по принципу действия, так и
по применению:
1. Электромеханические приборы – относительно простые, относительно точны
и не требуют для своей работы внешнего источника питания. Это приборы, у
которых под действием измеряемой величины возникает механическая энергия
поворота:
𝑥𝑥 ? → 𝑊𝑊мех → 𝛼𝛼 → 𝑥𝑥п − показания прибора
𝑥𝑥 ≡ 𝑊𝑊эл
┌ Электромеханический прибор состоит из трех частей: измерительная цепь,
измерительный механизм, отсчетное устройство.
Измерительная цепь служит для преобразования измеряемой электрической
величины в другую электрическую величину, непосредственно воздействующую на
измерительный механизм. В измерительном механизме электрическая энергия
преобразуется в механическую энергию, что приводит к перемещению (повороту)
подвижной части. Отсчетное устройство служит для визуального отсчитывания
значений измеряемой величины в зависимости от угла поворота подвижной части.
Так как в измерительном механизме обычно имеет место угловое перемещение
подвижной части, то при анализе их работы рассматриваются моменты,
действующие на подвижную часть. Моменты подразделяются на статические и
динамические. Статическими являются моменты, действующие в механизме
всегда при наличии измеряемой величины (это вращающий и
противодействующий моменты). Динамические моменты действуют на
подвижную часть только при во время ее движения (это момент сил инерции и
момент успокоения).┘
┌Магнитоэлектрические приборы состоят из магнитоэлектрического измерительного
механизма с отсчетным устройством и измерительной цепи. Эти приборы применяются
для измерения постоянных токов и напряжений, сопротивлений, количества
электричества (баллистические гальванометры и кулонметры), магнитного потока, также
для измерения или индикации малых токов и напряжений, кроме того они используются
для регистрации электрических величин (самопишущие приборы и осциллографические
гальванометры).┘
14
2. Электромагнитные приборы
Неподвижная катушка с током с подвижным сердечником.
Применяется и на постоянной, и переменной частоте 50 Гц, 400 Гц
┌Электромагнитные приборы состоят из электромагнитного
измерительного механизма с отсчетным устройством и измерительной
цепи. Они применяются для измерения переменных и постоянных токов,
и напряжений, для измерения частоты и фазового сдвига между переменными токами
и напряжением.
Измерительный механизм. Вращающий момент в этих механизмах возникает в
результате взаимодействия полей одного или нескольких ферримагнитных
сердечников подвижной части и магнитного поля катушки, по обмотке которой
протекает ток.
Электромагнитные измерительные механизмы могут работать в цепях постоянного,
так и переменного тока (примерно до 10 кГц).┘
3. Электродинамический прибор
Применяется и на постоянной, и переменной
частоте.
Самый высокоточный прибор на
переменном токе.
┌ Принцип действия электродинамических
приборов основан на взаимодействии
магнитных полей двух катушек одной,
неподвижно закрепленной, и другой,
сидящей на оси и могущей поворачиваться.
Г) Ферродинамическое устройство
Применяется преимущественно на переменном токе
примерно частотой 50 Гц, 400 Гц!!!
Может работать на постоянном, класс точности
составляет 0,5.
Достоинства:
1)
Обладает большим механическим моментом и
может работать в условиях вибрации и тряски.
2)
Используется на кораблях, в самопишущих
приборов.
Д) Электростатический прибор
Работает на переменном токе.
Достоинства:
Очень широкий частотный диапазон (200 кГц).
Это прибор, который может измерять киловольметры, но может
измерять маленькие В.
15
Ж) Индукционный прибор
Работает на переменном токе, частотой 50 Гц
Измеряет энергию (W, кВт*час)
Достоинства:
Высокочастотный прибор (класс точности 0,2)
┌Принцип действия индукционных измерительных механизмов основан на
взаимодействии переменных магнитных потоков и вихревых токов,
индуктированных магнитными потоками в подвижной части, выполненной в виде
алюминиевого диска.┘
З) Магнитоэлектрический преобразователь
1) Выпрямительный преобразователь
Пример прибора: тестер (мультиметр), может измерять I, U, R,
C.
Работает на частоте 20кГц
2)
Диод – устройство,
которое выпрямляет
Термоэлектрический преобразователь
Прибор может измерять токи частотой f=1МГц
3) Электронный преобразователь – самостоятельная
группа приборов, не относится к магнитоэлектрическим
приборам
Используется в усилителях.
Термопара
Лампочка - триод
Примечание: все приборы на переменном токе измеряют
действующее значение, кроме выпрямителя (з, 1) - он
измеряет среднее значение.
Можно ли померить мгновенное значение?
Достоинства электронных приборов:
1. Высокая чувствительность
2. Широкий частотный диапазон
3. Универсальные, т.е. могут все измерить
4. *только для электронных вольтметров, т.к. у них большое
входное сопротивление.
?? Почему 4* - это достоинство? ??
Недостатки:
1. Сравнительно невысокий класс точности, но
современная техника позволяет повысить
точность измерений электронными приборами.
16
2. Должен быть блок питания
ЭП – электронный прибор (много
схем внутри)
ЭС – электронная схема
УК – устройство калибровки
(установка нуля и калибровки как
таковой)
ППИ – переключатель пределов
измерений
БП – блок питания
м/э им – магнитоэлектрический измерительный механизм
Примечание: кабель позволяет повысить помехозащищенность прибора.
Электронная схема (ЭС)
1. Масштабный преобразователь (пассивные (уменьшают сигнал), например,
делители напряжения, шунты; активные (увеличивают сигнал: усилитель).
2. Преобразователи спектра - преобразуют один вид сигнала в другой
(постоянный в переменный и наоборот).
Например:
Модулятор: постоянный ток → переменный ток
Демодулятор: переменный ток → постоянный ток. Обычно демодуляторы – это
выпрямительные устройства, детекторы, синхронные детекторы.
3. Функциональные преобразователи (интеграторы, дифференцирующие
устройства, квадраторы).
4. Преобразователи импеданса (могут уменьшать/увеличивать входное
сопротивление)
5. Обратные (обращенные) преобразователи (выполняют обратную
функцию:x→1/x. интегратор-дифференциатор)
6. Преобразователи информативного параметра - под этим понятием чаще всего
принимают операции модуляции (амплитудную, фазовую, частотную).
Устройство калибровки (УК)
1) Установка нуля – это первая операция, которая производится перед
измерениями.
У современных приборов
автоматическая установка нуля.
2) Калибровка
Она также проводится перед
измерением.
Выставить калибровочную точку К, потом
перетащить указатель в точку К или красную К.
Калибровка может осуществляться и
автоматически.
Для повышения точности и упрощения работы с
приборами используют микропроцессорные
устройства.
Цифровые измерительные приборы (ЦИП)
Достоинства:
1) Высочайшая точность
17
2) Высокая чувствительность
3) Универсальность
4) Широкий частотный диапазон
5) ! возможность работы с компьютером
Недостатки:
1) Требуют источника питания
2) Требуют большого прогрева (больше часа)
3) Дорогие
4) Напичканы многими приборами, схемами
5) Обладают сравнительно невысокой надежностью
АУ – аналоговое устройство
АЦП – аналогово цифровой
преобразователь
Примечание: помимо чисто
аналоговых и чисто цифровых
существуют дискретноаналоговые приборы и
дискретно-цифровые.
У этих приборов отсчет
воспринимается как
аналоговый, кроме того, у
него имеется чисто цифровой
отсчет.
(рис шкалы)
Приборы на новых физических эффектах
ВУ – воздействующее устройство (влияет на индикаторное вещество (ИВ), меняет
свои оптические свойства) – тепловые, магнитные, химические.
Существуют газовые трубки, в которой газ может светиться под действием
напряжения. Грань между светом и тьмой – это указатель.
Отсчетное устройство состоит из ИВ, на которое влияет воздействующая величина х,
но отсчетное устройство должно иметь шкалу и указатель.
Данная шкала размещается под ИВ с указателем.
Достоинства:
Хорошо работают в условиях вибрации и тряски.
Недостатки:
Могут измерять только при больших значениях.
┌ Измерительная установка (ИУ) —
совокупность средств измерения и
вспомогательных устройств, предназначенная для рационального проведения
измерительного эксперимента (ИЭ). Лабораторный стенд
18
Информационно-измерительная система (ИИС) — совокупность конструктивно и
функционально объединенных средств измерения и вспомогательных устройств для
автоматического сбора измерительной информации от ряда источников для
дальнейшего преобразования, хранения, передачи и использования.┘
6. Классификация методов измерений
1. Методы непосредственной оценки – когда измеряемая величина
непосредственно измеряется конкретным прибором, шкала которого была
заранее градуирована с помощью многозначной меры, воспроизводящей
известные значения измеряемой величины.
2. Методы сравнений
2.1.1 Метод непосредственного сравнения
2.1.2 Метод опосредственного сравнения
2.2.1 Метод одновременного сравнения
2.2.2 Метод разновременного сравнения
2.3.1 Нулевой метод
2.3.2 Дифференцированный (разностный) метод
2.3.3 Метод совпадения
1.Метод непосредственной оценки – когда измеряемая величина измеряется
непосредственно конкретным прибором.
Пример:
X=I
—> [A]. Максимум шкалы 3 А. Показывает какое-то значение до 3 А.
X =V
—> [B]
X = t°
—> [°C]. Максимум шкалы сопротивления 250 R. Значение
показывает 150 R.
Этот метод менее точен, чем дальнейшие. Его точность определяется точностью
прибора.
2. Методы сравнения - позволяют повысить точность измерений.
Предполагает выполнение нескольких операция:
1) Подача измеряемой величины x
2) Наличие образцовой высокоточной величины 𝑥𝑥0
3) Наличие сравнивающего устройства (СУ)
4) Выполнение операции сравнения, когда измеряемая величина x сравнивается с 𝑥𝑥0
до определённого значения (до 0 или
какого-то другого значения).
5) Образцовую величину 𝑥𝑥0 мы должны
иметь способность менять.
В результате об измеряемой величине мы
судим по образцовой величине, известной с
высокой точностью.
Образцовые величины
Для переменного тока:
𝑥𝑥0 – образцовые волны
1. 𝑓𝑓0 – образцовые частоты
19
С высшей точностью
2. Синусоидальный генератор
Точный, но не очень
3. Меандр образцовый
A-var
T-var
Для постоянного тока:
1. Химический элемент, вырабатывает ЭДС. E = 1,2 … (15 знаков после запятой).
2. Источник калиброванный
𝑈𝑈0 = var
С высокой степенью точности.
3. Образцовая катушка 𝑅𝑅0
Значение может быть 10 Ом ± 0,01. Значения кратны 10
4. Магазин образцовых сопротивлений
Магазин сопротивлений – это прибор при помощи которого в цепь гальванического
тока можно ввести любой величины сопротивление току. Выглядит этот прибор как
20
ящик со множеством резисторов внутри. С помощью верньеров на лицевой панели
прибора можно выставить любое интересующее нас сопротивление.
Каждая черточка на круге (верньере) магазина сопротивлений – число от
нуля до десяти. Таким образом, настраивая ручки можно добиться любого
возможного целого сопротивления (здесь – целого, а вообще на магазинах
есть и десятые доли, и сотые доли Ома).
R0max (в данном случае) = 9999 Ом
R0min = R0нач (т.е. смотрим на маркировку)
R0min = 0,01 Ом (цифровая)
5. Магазин образцовых С𝟎𝟎 (Цифровой измеритель ёмкости-предлагаемый прибор
позволяет измерять емкость конденсаторов в диапазоне 1...10000 мкФ. Он портативен
и потребляет от девятивольтовой батареи всего 7 мА. Принцип роботы прибора
основан на измерении продолжительности разряда конденсатора при фиксированных
уровнях заряда и разряда.)
6. Магазин образцовых 𝐿𝐿0 (схемка попроще )
Классификация
1. Непосредственное сравнение
Сравниваемые величины должны быть
одной природы.
Сравнение измеряемой величины и образца
производится без «посредников».
На вход сравнивающего устройства (СУ)
подается измеряемая величина, которая
сравнивается с образцовой, известная с
высокой точностью. Причём об измеряемой величине судят по значению образцовой.
∆𝑋𝑋 = 𝑋𝑋 − 𝑋𝑋0
21
2. Опосредственное сравнение
Сравниваемые величины должны быть
одной природы (на рис – это кривая со
стрелками).
В данном случае входная величина
проходит через преобразователь.
3. Одновременное сравнение
Сравнение происходит в одно и тоже время.
4. Разновременное сравнение
Пример 1:
Классическим представлением разновременного
сравнения является метод замещения.
А)
Померили сопротивление, получили нечто неопределённое между десятью килоомами
и ста килоомами, поставили в этом месте на шкале точку.
И вот здесь-то нам и пригодится метод сравнения.
Б)
где R0 – это магазин сопротивлений, П –
переключатель (ключ).
Сначала переключатель включаем к
сопротивлению Rx. Омметр показывает
сопроивление XП. Ставим переключатель к R0. Мы
начинаем крутить сопротивления и проверять
подходит ли сопротивление магазина нашему
померенному сопротивлению (помним, у нас на шкале стоит точка между десятью и
ста килоомаи). Когда совпало – всё - замечательно, мы нашли сопротивление Rэлемента в схеме.
22
Пример 2:
x = Rx
+ 1) П → 1
𝑈𝑈
𝐼𝐼𝐴𝐴 =
𝑅𝑅𝑥𝑥
2) П → 2
𝑈𝑈
𝐼𝐼𝐴𝐴′ =
𝑅𝑅0
𝐼𝐼′
𝐼𝐼𝐴𝐴 *𝑅𝑅𝑥𝑥 =𝐼𝐼𝐴𝐴′ *𝑅𝑅0 =>𝑅𝑅𝑥𝑥 =𝑅𝑅0 𝐴𝐴
𝐼𝐼𝐴𝐴
Точность более высокая, поскольку применили R0.
Погрешность измерения определяется погрешностью
амперметра.
Разделение методов по результатам:
1. Нулевой метод:
∆x= x-𝑥𝑥0 =0
сравнение происходит до нуля
2. Дифференцированный (разностный)
∆x= x-𝑥𝑥0 ≠0
3. Метод совпадения
О результате судят по сопадению ометок от образцовой и от измеряемой величин.
Метод совпадений. Пример
Прибор пирометр оптический:
tВЫПЛАВЛЕНИЯ = tx. (Измерить бесконтактным методом очень высокую температуру)
Есть расплавленное тело. Чтобы узнать, нагрелось ли это тело до необходимой для,
например, выплавки стали, температуры, её, эту температуру, необходимо измерить.
Термометром не померишь ибо, когда дело доходит до нескольких тысяч градусов –
термометр расплавится, термопарой тоже не померишь – она привариться к стенкам
чана. Тогда придумали вот что: берут нить накала и, с помощью оптики, проецируют
её на расплавленное тело. Если температура тела и раскалённой нити одинакова
(читай: тело нагрелось до оптимальной температуры), нить будет не видна.
1. R1=var, I0=var
tнити=t0-var
Яркость нити меняется.
2. Делаем до тех пор, пока нит не будет видна:
tнити=tx
23
(I – знаем, t0 – находим)
Нулевой метод. Пример
СУ должно обладать высококой
чувствительностью
Пример 1. Идея:
Напряжения должны иметь встречное
включение.
СУ – нуль-индикатор, обладает высокой
чувствительностью.
7. Нулевой метод на примере потенциометра постоянного тока
Нулевой метод. Пример
СУ должно обладать высококой
чувствительностью
Пример 2: Потенциометр постоянного
тока с ручным уравновешиванием (для
измерения постоянного напряжения и
единственный прибор для измерения
ЭДС).
E0 – образцовое
напряжение;
Ux – измеряемое
напряжение;
Uвсп – вспомогательное
напряжение;
R0 – образцовое
сопротивление;
Rk – образцовое переменное
сопротивление;
НИ – нуль-индикатор;
П – переключатель.
I р .т.
U всп
var =
R0 + Rk + R р.т.
рабочий ток
1. П → 1
Установка рабочего тока с помощью
R р.т. → var до тех пор, пока IНИ = 0
=
E0 I р.т. ⋅ R0
24
I р .т. =
E0
высокая точность
R0
2. П → 2
Измерение Ux
Rk – var до тех пор, пока IНИ = 0
Когда же Ux = Uок ;
U=
I р.т. ⋅ Rk *
ок
U=
x
E0
⋅ Rk *
R0
Алгоритм измерения E0 заключается в следующем. Устанавливаем значение рабочего
тока, для чего переключатель П переводят в положение 1 (контур 1 называется контур
сравнения), а сопротивление RРТ изменяют до тех пор, пока СУ не покажет отсутствие
тока, тогда 𝐼𝐼РТ ∗ 𝑅𝑅0 = 𝐸𝐸0 = 𝑈𝑈0 .
Затем, переключатель П переводят в положение 2 (контур 2 – тоже называется
контуром сравнения) и, перемещая контакт на RX, добиваются отсутствия тока в
гальванометре (на нуль-индикаторе). В этом
случае 𝐼𝐼РТ ∗ 𝑅𝑅𝑋𝑋 = 𝑈𝑈𝑋𝑋 = 𝑈𝑈0 ∗ , где I – значение
рабочего тока, установленного ранее, т.е.
окончательно можно записать:
𝑅𝑅𝑋𝑋
𝑈𝑈𝑋𝑋 = 𝐸𝐸0 ∗
𝑅𝑅0
Примечание: измеряемая Е – ЭДС
Эквивалентная схема источника:
Чистая ЭДС
r– внутренне сопротивление ЭДС.
8. Нулевой метод на примере моста постоянного тока. Мосты равновесные
и неравновесные.
Предназначен для высокоточного измерения сопротивлений от 10 Ом до 105 Ом.
Мост – схема, имеющая не менее двух диагоналей.
Ri – сопротивления плеч (диагоналей)
моста.
НИ – нуль-индикатор, должен
обладать высокой чувствительностью
по постоянному току.
Стрелка по ветви НИ – IНИ
┌Обычно, в таких схемах третье и
четвёртое сопротивление являются
образцовыми и постоянными. ┘
Положение
Мост в равновесии, тогда и только
тогда, когда IНИ = 0, φа=φб.
Когда же это возможно?
RНИ → ∞ (ну, или, по крайней мере,
очень велико)
25
𝐼𝐼1 =
𝑈𝑈пит
𝑅𝑅1 +𝑅𝑅2
𝑈𝑈пит
𝐼𝐼 2 =
𝑅𝑅3 +𝑅𝑅4
𝑈𝑈𝑅𝑅1 = 𝐼𝐼1 ∙ 𝑅𝑅1 =
𝑈𝑈пит
𝑅𝑅1 +𝑅𝑅2
𝑈𝑈пит
𝑈𝑈𝑅𝑅4 = 𝐼𝐼2 ∙ 𝑅𝑅4 =
∙ 𝑅𝑅1
𝑅𝑅3 +𝑅𝑅4
∙ 𝑅𝑅4
Ток IНИ = 0, если UR1 = UR4 ⇒ R1∙R3=R2∙R4 *
Выражение (*) называется условием равновесия моста.
Вместо R1 - RX = ?
Добиваемся, чтобы IHИ было равно или стремилось к
нулю.
Плечо сравнения
Для этого
R2 – variable
𝑅𝑅
Если IНИ =0, то RX = R1 = R2 ∙ 4
**
𝑅𝑅3
Плечо отношения
R2, R3, R4 – известны с высокой точностью (образцовые
сопротивления).
Условие равновесия зависит от напряжения питания.
┌Примечание
1) UПИТ - variable ↓
2) RX (определяется) 100 Ом┘
Существуют специальные мосты для измерения малых сопротивлений.
RПРОВОДА – сопротивление провода
RК – сопротивление контакта
Поскольку искомое RX мало, сопротивление
провода и сопротивление контакта могут
испортить общую картину измерений.
𝑅𝑅
𝑅𝑅𝑋𝑋 + 2𝑅𝑅пр + 2𝑅𝑅к = 𝑅𝑅2 ∙ 4 ***
𝑅𝑅3
В этом примере имеют влияние
сопротивление контактов и проводов. На
точность контакта влияет сопротивление
изоляции.
Для измерения малых сопротивлений
используют малые мосты.
Неравновесный мост постоянного тока
Неравновесный мост постоянного тока. Применяется
для разбраковки сопротивления относительно
номинала.
Идеал: Rx=Rном
Реально: RX = RX НОМ +ΔR
Работа:
1)
RX = RНОМ = 1 кОм и мост
уравновешивается.
Добавляем IНИ → 0 и R2 →
variable
2)
RX = RНОМ ± ΔR мост
выходит из состояния равновесия
IНИ ≠ 0
3)
IНИ = F(ΔR) (т.е. функция от «дельта эр»)
26
9. Потенциометр переменного тока
Предназначен для измерения напряжения переменного тока с достаточно высокой
точностью, но менее точен, чем потенциометр постоянного тока из-за отсутствия
высокоточных образцов переменного тока.
Рассмотрим двухкоординатный потенциометр переменного тока.
Идея:
𝑈𝑈̇ = 𝑈𝑈 ∗ 𝑒𝑒 −𝑗𝑗𝑗𝑗
𝑈𝑈̇ = 𝑈𝑈𝑥𝑥 −?
R0X и R0Y – переменные высокоточные сопротивления, по ним производится расчет
напряжения.
M – катушка взаимной индуктивности
R – вносит поправку на частоту
НИ – нуль-индикатор
Работа:
1) Выставляем ток I1 с помощью амперметра и Rр.т. не компенсационным путем
U0X = R0X*∙I1
2)
I2 = (j ∙ 𝝎𝝎 ∙ M ∙ I1)/(R0Y + R)
E= j ∙ 𝝎𝝎 ∙ M ∙ I1
Угол между I1 и I2 равен девяноста градусам.
U0Y = I2 ∙ R0Y*
3)
27
Попеременно регулируя R0X и R0Y добиваемся тока через индуктор равного нулю.
𝑈𝑈
2
2
𝑈𝑈𝑋𝑋 = �𝑈𝑈0𝑋𝑋
+ 𝑈𝑈0𝑌𝑌
φx = arctg 0𝑌𝑌
𝑈𝑈0𝑋𝑋
Высокая точность, если на входе и выходе сигналы одного вида (это может быть
треугольник, меандр, трапеция, синусоида).
┌
Замечание;
Что будет, если UX будет не синусоидальной, а, например, такой:
Всё просто: рассматриваем ещё несколько гармоник, кроме первой.┘
10. Мосты переменного тока
Мост переменного тока предназначен для
измерения емкости (С), тангенса угла потерь
(tgδ), индуктивности (L), добротности (Q),
магнитной проницаемости (μ).
НИ – должен реагировать на переменный ток.
НИ=0: условие равновесия:
𝑍𝑍1 ∗ 𝑍𝑍3 = 𝑍𝑍2 ∗ 𝑍𝑍4
𝑍𝑍1 = 𝑧𝑧1 ∗ 𝑒𝑒 𝑗𝑗∗𝜑𝜑1
𝑍𝑍2 = 𝑧𝑧2 ∗ 𝑒𝑒 𝑗𝑗∗𝜑𝜑2
𝑍𝑍3 = 𝑧𝑧3 ∗ 𝑒𝑒 𝑗𝑗∗𝜑𝜑3
𝑍𝑍4
𝑗𝑗∗𝜑𝜑4
= 𝑧𝑧4 ∗ 𝑒𝑒
Тогда выражение для условия равновесия
моста принимает вид 𝑧𝑧1 ∗ 𝑧𝑧3 ∗ 𝑒𝑒 𝑗𝑗∗(𝜑𝜑1+𝜑𝜑3) =
𝑧𝑧2 ∗ 𝑧𝑧4 ∗ 𝑒𝑒 𝑗𝑗∗(𝜑𝜑2+𝜑𝜑4)
Два комплексных числа равны, если равны
их модули и фаза:
𝑧𝑧1 ∗ 𝑧𝑧3 = 𝑧𝑧2 ∗ 𝑧𝑧4
𝜑𝜑1 + 𝜑𝜑3 = 𝜑𝜑2 + 𝜑𝜑4
Пример: измерение емкости конденсатора
Емкости делят на:
• емкости с большими потерями;
• емкости с малыми потерями.
Соответственно, для емкостей с малыми потерями используется последовательная
эквивалентная схема:
R
С
а для емкостей с большими потерями — параллельная:
28
R
С
Для последовательной схемы полные сопротивления плеч моста имеют вид
1
1
, Z2 =
, Z 3 ==
Z1 =
Rx +
R0 +
R3 , Z 4 R4 ,
jωCx
jωC0
а условие равновесия записывается как
( Rx + 1 jωCx ) R3 =
( R0 + 1 jωC0 ) R4 ,
откуда Cx C=
=
R0 R4 R3 , ┌а тангенс угла потерь равен=
tg δ ω=
Cx Rx ωC0 R0 . ┘
0 R3 R4 , Rx
Для последовательной схемы полные сопротивления плеч моста имеют вид
1
, Z2 =
Z1 =
Rx +
R2 , Z 3 =
R0 + jω L0 , Z 4 =
R4 ,
jωCx
а условие равновесия записывается как
1
R2 * R4
Rx +
* ( R0 + jω L0 ) =
jωCx
29
11. Дифференциальный метод измерения на примерах
Дифференциальный метод менее точный, чем нулевой, но более точный, чем метод
непосредственного измерения. Д.М. позволяет измерить приращение измеряемой
величины относительно номинального значения.
Пример 1:
UХ=UС = 110 В ± 10% (от 110 В);
UНОМ = 110 В; ΔU = (-11)В ≑ (+11) В
X = UС = ?
Прямое измерение
Не можем измерить отклонение
Дифференциальный метод
Образцовое напряжение подключено встречно. Приращение относительно
номинального.
Измеряем приращение относительно номинального значения.
Пример 2: Тут пример
неравновесного моста, который
расписан в 8 вопросе.
Пример 3:
Задача: определение
неравномерностей магнитных полей.
Магнитное поле замеряют специальным прибором, называемым датчиком Холла.
Выглядит он следующим образом.
3,4 – эквипотенциальные зажимы.
Датчик или преобразователь Холла (ПХ) является гальваномагнитным
преобразователем, в котором под действием магнитного поля возникает ЭДС. Датчик
представляет собой пластину из полупроводника, по которой течёт ток I. При
помещении пластины в магнитное поле, вектор магнитной индукции B которого
перпендикулярен плоскости пластины, на боковых гранях её возникает разность
потенциалов – ЭДС Холла:
30
Ex=SB*B=SI*I*B, SB – чувствительность по току.
После усиления ЭДС Холла измеряется компенсатором постоянного тока или
милливольтметром mV, шкала которого проградуирована в единицах магнитного
потока при условии постоянства силы тока.
Преобразователи Холла имеют малые размеры, что позволяет проводить измерение
индуктивности магнитного поля в малых зазорах.
Идеальная модель
Реальная модель
12. Структурные схемы средств измерений прямого преобразования
Структурная схема СИ прямого преобразования
S – Чувствительность
x1=S1X, X2=S2X
Каждый Пi характеризуется функцией преобразования (линейной или нелинейной).
X1=K1X
X2=K2X
и т.д.
Рассмотрим случай, когда функция преобразования является линейной (для
нелинейной ФП – всё то же самое, только дольше и больше).
Зависимость входной величины от входной 𝑋𝑋𝑛𝑛 = 𝑓𝑓(𝑋𝑋).
Легко видеть, что:
𝑋𝑋𝑛𝑛 = 𝑘𝑘1 ∗ 𝑘𝑘2 ∗ 𝑘𝑘3 ∗ … ∗ 𝑘𝑘𝑛𝑛 ∗ 𝑋𝑋
*
31
Вот это назовём коэффициентом преобразования
для всего устройства и обозначим К
𝐾𝐾 = 𝑘𝑘1 ∗ 𝑘𝑘2 ∗ 𝑘𝑘3 ∗ … ∗ 𝑘𝑘𝑛𝑛
**
В этой схеме возникают два вида погрешностей:
1) ∆м – мультипликативная (погрешность чувствительности)
2) ∆а – аддитивная (погрешность нуля)
Рассмотрим мультипликативную погрешность:
Мультипликативная погрешность возникает из-за того, что коэффициенты
преобразования отдельных блоков схемы могут меняться.
𝑘𝑘1 + 𝛥𝛥𝑘𝑘1
𝑘𝑘2 + 𝛥𝛥𝑘𝑘2
…
→ 𝐾𝐾 + 𝛥𝛥𝛥𝛥 → Δм
𝑘𝑘𝑛𝑛−1 + 𝛥𝛥𝑘𝑘𝑛𝑛−1
𝑘𝑘𝑛𝑛 + 𝛥𝛥𝑘𝑘𝑛𝑛
┌ Прологарифмируем выражение
**…
ln(𝐾𝐾) = ln(𝑘𝑘1 ) + ln(𝑘𝑘2 ) + ln(𝑘𝑘3 ) + ⋯ + ln(𝑘𝑘𝑛𝑛 )
… и возьмём производную от последнего┘
***
∆𝐾𝐾 ∆𝐾𝐾1 ∆𝐾𝐾2
∆𝐾𝐾𝑛𝑛−1 ∆𝐾𝐾𝑛𝑛
=
+
+ ⋯+
+
𝐾𝐾
𝐾𝐾1
𝐾𝐾2
𝐾𝐾𝑛𝑛−1
𝐾𝐾𝑛𝑛
Рассмотрим, к чему это приведет:
Исходное (идеальное): 𝑋𝑋𝑛𝑛 = 𝐾𝐾 ∗ 𝑋𝑋, где X = const
Но в действительности из-за мультипликативной погрешности:
𝑋𝑋𝑛𝑛∗ = (𝐾𝐾 + ∆𝐾𝐾) ∗ 𝑋𝑋
𝑋𝑋𝑛𝑛∗ − 𝑋𝑋𝑛𝑛 = ∆𝐾𝐾 ∗ 𝑋𝑋, где X = const.
Вывод: из-за наличия мультипликативной погрешности выходной сигнал изменяется.
Таким образом, «благодаря» мультипликативной погрешности выходной сигнал по
отношению к входному будет изменён в ∆𝐾𝐾 раз.
Рассмотрим аддитивную погрешность:
Аддитивная погрешность возникает из-за внешних помех и внутренних дрейфов.
Внешние помехи
Δа
Обозначим через XПОМЕХ = XПОМ
Внутренний дрейф
Помеха непредсказуема, она может появиться в любой точке схемы. Но, вот если
она попадает на вход – это самое «страшное», ибо она, помеха, пройдёт через всю
цепь как полезный сигнал и искажения будут чудовищными (ибо на входе уже
искажённый сигнал). Не будем рассматривать этот случай, берём в скобках…
Приведём все помехи ко входу устройства (как показано пунктирными линиями на
схеме со стрелкой):
𝑋𝑋ПОМ (𝑛𝑛−1)
𝑋𝑋
𝑋𝑋
𝑋𝑋ПОМ 𝑛𝑛
∆𝑋𝑋а = ПОМ 1 + ПОМ 2 + ⋯ +
+
****
𝑘𝑘1
𝑘𝑘1 ∗𝑘𝑘2
𝑘𝑘1 ∗𝑘𝑘2 ∗…∗𝑘𝑘(𝑛𝑛−2) ∗𝑘𝑘(𝑛𝑛−1)
𝑘𝑘1 ∗𝑘𝑘2 ∗…∗𝑘𝑘(𝑛𝑛−1) ∗𝑘𝑘𝑛𝑛
Выводы:
1. Видно, что наиболее опасные с точки зрения помех – первые каскады устройства.
2. Попадание помехи на вход – катастрофа, нужно принять меры – кабели, заземление
или применение специальных фильтров. Правда использование фильтров может
привести к ухудшению динамики реакции.
32
3. Формула **** позволяет сопоставить влияние помехи относительно входного
сигнала.
Пример:
Пускай n = 3 блока. Пусть k1 = k2 = k3 = 10
Подали на вход X = 1000 мВ = 1 В, а, в то же время,
XПОМ 1 = XПОМ 2 = XПОМ 3 = 1 В.
Приводим все погрешности ко входу устройства:
𝑋𝑋ПОМ 1 𝑋𝑋ПОМ 2
𝑋𝑋ПОМ 3
1
1
1
∆𝑋𝑋а =
+
+
=
+
+
= 0,111 В
𝑘𝑘1
𝑘𝑘1 ∗ 𝑘𝑘2 𝑘𝑘1 ∗ 𝑘𝑘2 ∗ 𝑘𝑘3 10 100 1000
┌А для чего вообще мы всё это делаем (приводим ко входу помехи)?
Да причина проста: мы желаем сопоставить величину суммарной помехи системы и
значение входной величины, чтобы понять: система, вообще, имеет хоть какой-то
смысл или нет.
Выводы:
1) В принципе, число n должно быть конечным (количество элементов должно быть
ограничено);
2) Первый каскад необходимо сделать грамотно (как и все остальные, разумеется, но к
первому – первостепенное внимание, ибо он самый помехоопасный);
3) Можно улучшить характеристики: постараться подобрать параметры элементов таким
образом, чтобы уменьшить погрешность.┘
13. Структурные схемы средств измерений компенсационного
преобразования с астатической характеристикой
Совокупность блоков ОСi представляет собой цепь отрицательной обратной связи, в
которой информация проходит в противоположном основной цепи направлении.
Обозначения:
СУ – сравнивающее устройство
𝜷𝜷i – коэффициент преобразования ЦОС (цепи обратной связи)
Ki – коэффициент преобразования ЦПП (цепи прямого преобразования или ЦПС – цепи
прямой связи)
Цепь замкнута с выхода на вход (принцип ЦОС) и состоит из цепи прямого
преобразования с коэффициентом преобразования:
𝐾𝐾 = 𝑘𝑘1 ∗ 𝑘𝑘2 ∗ 𝑘𝑘3 ∗ … ∗ 𝑘𝑘𝑛𝑛
и цепи обратной связи с коэффициентом преобразования:
𝛽𝛽 = 𝛽𝛽1 ∗ 𝛽𝛽2 ∗ 𝛽𝛽3 ∗ … ∗ 𝛽𝛽𝑚𝑚
Пускай ∆𝑋𝑋 – сигнал рассогласования или разностный сигнал
∆𝑋𝑋 = 𝑋𝑋ВХ − 𝑋𝑋ОС .
33
Такая система может работать в двух режимах. В зависимости от ∆𝑋𝑋 различают:
• Астатический режим при ∆𝑋𝑋 = 0. Происходит полная компенсация 𝑋𝑋ВХ = 𝑋𝑋ОС
• Статический режим ∆𝑋𝑋 ≠ 0. Происходит неполная компенсация 𝑋𝑋ВХ ≠ 𝑋𝑋ОС
Рассмотрим астатический режим: ∆𝑋𝑋 = 𝑋𝑋ВХ − 𝑋𝑋ОС = 0.
Астатический режим может быть реализован только при наличии в цепи прямого
преобразования интегрирующего (запоминающего) звена (блока). Это звено может
стоять в любом месте ЦПП (цепи прямого преобразования). Однако, современные
интеграторы обладают сравнительно невысокой чувствительностью (требуют
большого сигнала) и ставятся в конце ЦПП.
Пускай интегрирующее звено ПИ
X n-1
Пи
Xn
𝑋𝑋𝑛𝑛 = � 𝐹𝐹(𝑋𝑋𝑛𝑛−1 )𝑑𝑑𝑑𝑑
Из-за него и не будет нуля на выходе (интегрирующее звено будет запоминать
дошедшее до него значение).
Найдём функция преобразования всего устройства 𝑋𝑋 = 𝐹𝐹(𝑋𝑋𝑛𝑛 ):
𝑋𝑋ОС = 𝛽𝛽 ∗ 𝑋𝑋𝑛𝑛
∆𝑋𝑋 = 𝑋𝑋 − 𝑋𝑋ОС
Решаем совместно и получаем зависимость:
1
𝑋𝑋𝑛𝑛 = ∗ 𝑋𝑋
𝛽𝛽
Последнее выражение справедливо как для всей цепи, так и для каждого отдельно
взятого блока.
Коэффициент передачи ЦПП вообще не попал в формулу.
Чувствительность всего устройства в целом не зависит от коэффициента
преобразования прямой цепи, а зависит только от коэффициента преобразования
обратной связи:
1
1
𝑆𝑆 = =
𝛽𝛽 𝛽𝛽1 ∗ 𝛽𝛽2 ∗ 𝛽𝛽3 ∗ … ∗ 𝛽𝛽𝑚𝑚
На практике цепь с отрицательной обратной связью можно сделать более точной, чем
цепь прямого преобразования (в ряде случаев не ставить усилители и т.д.)
В этой схеме возникают два вида погрешностей:
1) ∆м – мультипликативная
2) ∆а – аддитивная
Рассмотрим мультипликативную погрешность
┌Мультипликативная
𝛽𝛽1 + 𝛥𝛥𝛽𝛽1
𝛽𝛽2 + 𝛥𝛥𝛽𝛽2
𝛽𝛽𝑛𝑛−1 + 𝛥𝛥𝛽𝛽𝑛𝑛−1
𝛽𝛽𝑛𝑛 + 𝛥𝛥𝛽𝛽𝑛𝑛
…
→ 𝛽𝛽 + 𝛥𝛥𝛥𝛥 → 𝑆𝑆 + 𝛥𝛥𝛥𝛥 → ΔM
Из выражения для чувствительности ln(𝑠𝑠) = 𝑙𝑙𝑙𝑙(1) − ln(𝛽𝛽).┘
∆𝑆𝑆
∆𝛽𝛽1 ∆𝛽𝛽2 ∆𝛽𝛽3
∆𝛽𝛽𝑚𝑚
= −(
+
+
+ ⋯+
)
𝑆𝑆
𝛽𝛽1
𝛽𝛽2
𝛽𝛽3
𝛽𝛽𝑚𝑚
34
Введение отрицательной обратной связи всегда уменьшает мультипликативную
погрешность.
Рассмотрим аддитивную погрешность
Аддитивная
Внутренний дрейф
∆А
Внешние помехи
Обохначим Xпом
Зона нечувствительности или
порогочувствительность интегрирующего звена ∆𝑋𝑋инт
Поскольку цепь обратной связи чаще всего
выполняется низкоомной, то помеха на нее
практически не влияет.
Приведём все помехи и порогочувствительность ко
входу:
∆А =
𝑋𝑋ПОМ 1 𝑋𝑋ПОМ 2
𝑋𝑋ПОМ 3
𝑋𝑋ПОМ 𝑛𝑛
∆𝑋𝑋инт
+
+
+ ⋯+
+
𝑘𝑘1
𝑘𝑘1 ∗ 𝑘𝑘2 𝑘𝑘1 ∗ 𝑘𝑘2 ∗ 𝑘𝑘3
𝑘𝑘1 ∗ 𝑘𝑘2 ∗ 𝑘𝑘3 ∗ … ∗ 𝑘𝑘𝑛𝑛 𝑘𝑘1 ∗ 𝑘𝑘2 ∗ 𝑘𝑘3 ∗ … ∗ 𝑘𝑘𝑛𝑛−1
Значит, введение ООС не уменьшает аддитивную погрешность, а только
увеличивает её.
14. Структурные схемы средств измерений компенсационного
преобразования со статической характеристикой
Статический режим означает, что
∆𝑋𝑋 = 𝑋𝑋 − 𝑋𝑋ОС ≠ 0
В этом режиме не происходит полного сравнения.
Всё то же самое:
𝐾𝐾 = 𝑘𝑘1 ∗ 𝑘𝑘2 ∗ 𝑘𝑘3 ∗ … ∗ 𝑘𝑘𝑛𝑛
𝛽𝛽 = 𝛽𝛽1 ∗ 𝛽𝛽2 ∗ 𝛽𝛽3 ∗ … ∗ 𝛽𝛽𝑚𝑚
Решаем совместно систему из трёх уравнений, написанных выше:
∆𝑋𝑋 = 𝑋𝑋 − 𝑋𝑋ОС ≠ 0
𝑋𝑋𝑛𝑛 = 𝐾𝐾 ∗ ∆𝑋𝑋
𝑋𝑋ОС = 𝛽𝛽 ∗ 𝑋𝑋𝑛𝑛
*
Решаем систему и получаем решение в виде:
𝐾𝐾
*
∗ 𝑋𝑋
𝑋𝑋𝑛𝑛 =
1 + 𝐾𝐾 ∗ 𝛽𝛽
**
где чувствительность всего устройства в целом равна
35
𝐾𝐾
1 + 𝐾𝐾 ∗ 𝛽𝛽
***
и зависит от параметров как прямого преобразования, так и от параметров обратной
связи.
В схеме два вида погрешностей:
1) Мультипликативная – связана с коэффициентами изменения преобразования.
В уравнение зависимости входной величины от выходной попали коэффициенты
преобразования обоих цепей: и ЦОС, и ЦПП. Значит:
𝑘𝑘1 + ∆𝑘𝑘1
…
→ K + ΔK
𝑘𝑘𝑛𝑛 + ∆𝑘𝑘𝑛𝑛
→ S + ΔS → ΔM
𝛽𝛽1 + ∆𝛽𝛽1
…
→ 𝜷𝜷 + Δ𝜷𝜷
𝛽𝛽𝑚𝑚 + ∆𝛽𝛽𝑚𝑚
┌Задаёмся вопросом: как связать ΔK, Δ𝜷𝜷 и ΔS ?
Возьмём производную от выражения *** :
∆𝐾𝐾(1 + 𝐾𝐾 ∗ 𝛽𝛽) − ∆𝐾𝐾 ∗ 𝐾𝐾 ∗ 𝛽𝛽 − ∆𝛽𝛽 ∗ 𝐾𝐾 2
∆𝑆𝑆 =
(1 + 𝐾𝐾 ∗ 𝛽𝛽)2
┘
И тогда, нестабильность всего устройства (относительное изменение коэффициента
преобразования всего устройства):
1
∆𝐾𝐾
𝐾𝐾 ∗ 𝛽𝛽
∆𝛽𝛽
∆𝑆𝑆
****
=
∗
−
∗
1 + 𝐾𝐾 ∗ 𝛽𝛽 𝐾𝐾
1 + 𝐾𝐾 ∗ 𝛽𝛽 𝛽𝛽
𝑆𝑆
Причём,
∆𝐾𝐾
− нестабильность цепи прямого преобразования
𝐾𝐾
∆𝛽𝛽
− нестабильность цепи обратной связи
𝛽𝛽
«-» - чисто математический знак, сложение или вычитание зависит от ∆К и ∆β.
А {𝐾𝐾 ∗ 𝛽𝛽} называют петлевым усилением.
Пусть
1
∆𝐾𝐾
𝐾𝐾 ∗ 𝛽𝛽
∆𝛽𝛽
∗
обозначим а;
∗
обозначим б
1 + 𝐾𝐾 ∗ 𝛽𝛽 𝐾𝐾
1 + 𝐾𝐾 ∗ 𝛽𝛽 𝛽𝛽
Тогда строим график по равенству
:
𝑆𝑆 =
****
(𝐾𝐾 ∗ 𝛽𝛽)1
36
(𝐾𝐾 ∗ 𝛽𝛽)2
При (𝐾𝐾 ∗ 𝛽𝛽)1 преобразователь более устойчив, но менее точен. А при (𝐾𝐾 ∗ 𝛽𝛽)2 ,
наоборот – более точен, но менее устойчив.
Выводы:
1)
Если 𝛽𝛽 = 0, то погрешность определяется нестабильностью цепи прямого
преобразования
∆𝑆𝑆
∆𝐾𝐾 ∆𝛽𝛽
2)
− функция 𝑓𝑓( ; )
3)
𝑆𝑆
При 𝐾𝐾 ∗ 𝛽𝛽 ≫ 1 ,
𝐾𝐾
∆𝑆𝑆
𝑆𝑆
𝛽𝛽
∆𝛽𝛽
→
𝛽𝛽
:
• При больших петлевых усилениях нестабильность всего устройства в целом
определяется только нестабильностью цепи обратной связи. А цепь обратной
связи можно сделать стабильной, т.е. введение отрицательной обратной связи
уменьшает мультипликативную погрешность.
• Однако, при больших петлевых усилениях система может терять устойчивость
(реагировать не на полезный сигнал, а на помехи и шумы). Естественно, это
плохо. Посему, при создании таких устройств ищут компромисс между
точностью и устойчивостью.
2) Аддитивная погрешность
Случай с помехой на входе рассматривать не станем (причина была озвучена ранее:
помеха проходит через всю цепь, словно она – полезный сигнал).
Снова приводим все помехи ко входу:
𝑋𝑋ПОМ 3
𝑋𝑋ПОМ 𝑛𝑛
𝑋𝑋ПОМ 1 𝑋𝑋ПОМ 2
+
+
+⋯+
∆А = �
�−
𝑘𝑘1
𝑘𝑘1 ∗ 𝑘𝑘2 𝑘𝑘1 ∗ 𝑘𝑘2 ∗ 𝑘𝑘3
𝑘𝑘1 ∗ 𝑘𝑘2 ∗ 𝑘𝑘3 ∗ … ∗ 𝑘𝑘𝑛𝑛
−(𝑋𝑋ПОМ ОС 1 ∗ 𝛽𝛽2 ∗ 𝛽𝛽3 ∗ … ∗ 𝛽𝛽𝑚𝑚 + 𝑋𝑋ПОМ ОС 2 ∗ 𝛽𝛽3 ∗ 𝛽𝛽4 ∗ … ∗ 𝛽𝛽𝑚𝑚 + ⋯ + 𝑋𝑋ПОМ ОС 𝑚𝑚 )
Получаем, что отрицательная обратная связь (ООС) аддитивную погрешность не
уменьшает, т.к. ООС низкоомная. Необходимы конструктивные меры и решения по
повышению помехозащищённости.
37
15. Автоматический мост для измерения сопротивлений
Условные обозначения: УН – усилитель напряжения; УМ – усилитель мощности
(могут быть совмещены в одном приборе, как показано штриховкой); РД –
реверсивный двигатель; Ri – образцовое сопротивление. Причём R1 – переменное
сопротивление, движок которого перемещается механически с помощью редуктора,
управляемого реверсивным двигателем РД.
В качестве НИ используются УН и УМ, сигнал с которых поступает на РД.
Т.к. ~Uвх, то нет дрейфа.
Rx?→∆U≠0→Xn→kус∆U→∆U→R1=var, до тех пор, пока ∆U=0
Редуктор нужен, чтобы R1 менялся плавно и медленно.
┌Более подробное описание:
Схема предназначена для измерения сопротивления RX c высокой точностью (см.
«МОСТ» в нулевом методе).
Мосты с автоматизированным процессом уравновешивания называются
автоматическими мостами; они находят широкое применение для измерения и
регистрации величин. Автоматические мосты с дополнительным регулирующим
устройством применяют для автоматического управления производственными
процессами. В настоящее время широко распространены автоматические мосты для
измерения, регистрации и регулирования температуры различных объектов. В
качестве измерительного механизма в подобных мостах применяются
терморезисторы.
Схема автоматического моста для измерения сопротивления RX приведена на
рисунке выше. Мост питается от источника переменного напряжения питания UПИТ.
Если мост уравновешен, то напряжение между точками а и б равно нулю и ротор
двигателя РД неподвижен. При изменении измеряемого сопротивления RX на
диагонали моста (между точками а и б) появится напряжение, значение которого
зависит от RX. Это напряжение усиливается усилителями и подаётся на реверсивный
двигатель РД, который, через редуктор (причина, почему реверсивный двигатель
управляет движением резистора именно через редуктор очень проста: никто ведь не
управляет марионеточными куклами, привязывая ниточки к маховику автомобильного
38
двигателя, так и здесь: если всю энергию РД будет тратить на передвижение
резистора, то последний может просто вылететь из схемы, настолько сильный он
получит импульс), передвигает подвижный контакт переменного резистора R1 в
сторону достижения равновесия моста и одновременно поворачивает указатель (ведь
это же измерительный прибор), а при записи измеряемой величины – перемещает
перо, записывающее на диаграмме её значение. Ротор двигателя вращается до
достижения равновесия моста. Если автоматический мост предназначен для
управления, то тем же двигателем приводятся в действие регулирующие устройства.
Автоматизация процесса уравновешивания в мостах переменного тока значительно
сложнее. Автоматические мосты переменного тока для измерения и регистрации
комплексного сопротивления должный иметь два регулирующих элемента
(двигателя), которые обеспечивают два условия равновесия моста – по модулю и по
фазе. По точности автоматические мосты переменного тока уступают мостам
постоянного, всё из-за комплексности измерений и количестве элементов в
собираемой схеме.
Точность этой схемы определяется порогочувствительностью реверсивного
двигателя: чем она меньше, тем чётче будет работать система.┘
16. Электронный веберметр
Электронный веберметр (иначе – флюксметр) – это прибор, предназначенный для
измерения изменения постоянного магнитного потока.
Пусть, хотим померить
ΔФX, равное, естественно,
«вопрос».
Bx=Фх/S
Берём обмотку с
количеством витков равным
𝜔𝜔𝑛𝑛𝑛𝑛 , обмотку накручиваем на
нейтральное сечение,
подключаем обмотку на
нейтральное сечение и … ничего не
измеряется. То есть, веберметр вообще
ничего не показывает. А всё почему?
Да потому что веберметр – прибор для
измерения ИЗМЕНЕНИЯ магнитного
потока. Значит, следует как-то
рассоединить катушку без магнитного
потока и постоянный магнит, имеющий
свой магнитный поток. НУ, а сделать
это нетрудно. Есть два способа:
39
Таким образом, в первом случае А) веберметр будет показывать
∆Ф𝑋𝑋 = (Ф𝑋𝑋 − ФРАМКИ ) = (Ф𝑋𝑋 − 0)
разность между магнитным поток ФX постоянного магнита и магнитным поток
рамки, равным нулю. Короче говоря, положительное значение ∆Ф𝑋𝑋 .
В случае Б)
∆Ф𝑋𝑋 = (ФРАМКИ − Ф𝑋𝑋 ) = (0 − Ф𝑋𝑋 )
всё наоборот и отрицательно.
Принципиальная схема электронного веберметра
УН и УМ – усилитель напряжения и усилитель мощности, соответственно.
Элементы и обозначения:
Внутри устройства – рамка магнитоэлектрического гальванометра –
высокочувствительный прибор постоянного тока:
Чувствиетльность гальванометра достигает 𝐼𝐼Г = 10−16 𝐴𝐴
Верхняя из катушек, составляющих М-элемент (связанные катушки) является
катушкой вторичной обмотки.
В качестве нагрузки усилителя мощности имеется вторичная обмотка ИК,
амперметр, который проградуирован в мкВб.
40
RФ 1 и RФ 2 – фоторезисторы. То есть элементы, которые под воздействием света
изменяют свои проводящие свойства.
Работа схемы:
От лампы свет падает на зеркало гальванометра и отражается на фоторезисторы.
a. Исходно световые потоки и свет
Ф1 = Ф2 = Ф0
b. Необходимо найти ΔФX магнитный поток
При изменении потока, сцепляющегося с витками измерительной катушки ИК, на её
зажимах возникает ЭДС
𝑑𝑑Ф𝑋𝑋
𝑒𝑒𝑋𝑋 = −𝜔𝜔𝑛𝑛𝑛𝑛 ∗
𝑑𝑑𝑑𝑑
Зеркальце и лампочка создают световой отсчёт (заяц или световое пятно). Рамка,
под действием тока поворачивается в поле постоянного магнита, а вместе с ней,
поворачивается и зеркало (если рамка повернулась на угол α, то и зеркало повернётся
на угол α).
По действию ЭДС в цепи магнитоэлектрического гальванометра (обозначена на
рисунке) потечёт ток, при этом подвижная часть гальванометра повернётся, что
вызовет изменение светового потока, падающего на фотоэлементы (фоторезисторы), а,
следовательно, и фототока. Фототок усиливается благодаря усилителям (напряжение
пропорционально току). Выходной ток I усилителя преобразуется с помощью
дифференцирующего звена в виде М-элемента в напряжение обратной связи, которое
поступает в цепь измерительной катушки.
𝑒𝑒𝑋𝑋 → 𝐼𝐼Г → 𝛼𝛼
Ф1 = Ф0 − ∆Ф → 𝑅𝑅Ф 1 = 𝑅𝑅Ф 0 + ∆𝑅𝑅Ф 1
Ф2 = Ф0 + ∆Ф → 𝑅𝑅Ф 2 = 𝑅𝑅Ф 0 − ∆𝑅𝑅Ф 2
41
∆𝑈𝑈 ≠ 0 → 𝑘𝑘∆𝑈𝑈 → ∆𝐼𝐼𝐻𝐻
И вот сейчас появляется ЭДС обратной связи:
𝑑𝑑𝐼𝐼𝐻𝐻
𝑒𝑒ОС = −𝑀𝑀 ∗
𝑑𝑑𝑑𝑑
Всё это будет индексироваться, поворачиваться и появляться до тех пор, пока не
наступит статический режим, то есть до тех пор, пока не будет выполнено:
𝑒𝑒𝑋𝑋 ≈ 𝑒𝑒𝑂𝑂𝑂𝑂
Тогда,
𝜔𝜔𝑛𝑛𝑛𝑛 ∗ ∆Ф𝑋𝑋 = 𝑀𝑀 ∗ ∆𝐼𝐼𝐻𝐻
Таким образом,
𝜔𝜔𝑛𝑛𝑛𝑛
∆𝐼𝐼𝐻𝐻 =
∗ ∆Ф𝑋𝑋
𝑀𝑀
где 𝜔𝜔𝑛𝑛𝑛𝑛 - число витков катушки ИК; ∆Ф𝑋𝑋 - изменение измеряемого потока; 𝑀𝑀 постоянная цепи обратной связи.
Обнаруживаем зависимость
𝐼𝐼𝐻𝐻 = 𝑓𝑓(∆Ф𝑋𝑋 )
Таким образом, по силе тока I можно судить о потоке ФX. Шкалу миллиамперметра
градуируют в единицах магнитного потока.
17. Структурные схемы средств измерений с автоматической коррекцией
Идея:
┌Какие погрешности мы знаем: ∆a , ∆𝑀𝑀 , ∆a + ∆𝑀𝑀
Задача: уменьшить или устранить (этим и будем заниматься) возникающие
погрешности или, по крайней мере, учесть методами математический статистики (не
рассматриваем).
Знаем: ООС уменьшает мультипликативную погрешность ∆𝑀𝑀 . Необходимо узнать, как
устранить аддитивную погрешность ∆a и погрешность суммарную ∆a + ∆𝑀𝑀 .┘
1. Создание корректирующего сигнала 𝑌𝑌КОРР :
a. Схемно
b. С помощью компьютера
2. Вид корректирующего сигнала
𝑌𝑌КОРР = 𝐹𝐹(∆а ; ∆𝑀𝑀 ; ∆а + ∆𝑀𝑀 )
3. Должен вырабатываться автоматически
4. По входу устройства и по выходу
Пример 1:
Пусть есть измерительный преобразователь
ИДЕАЛ:
РЕАЛЬНО:
𝑌𝑌 = 𝑘𝑘НОМ ∗ 𝑋𝑋
𝑌𝑌 ∗ = (𝑘𝑘НОМ + ∆𝑘𝑘) ∗ 𝑋𝑋
Разница между реальным случаем и идеальным:
∆𝑌𝑌 = 𝑌𝑌 ∗ − 𝑌𝑌 = ∆𝑘𝑘 ∗ 𝑋𝑋 при 𝑋𝑋 = 𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐
Необходимо собрать следующую цепь:
42
Причём между Входной «иксовой»
величиной и величиной, подаваемой
в коррекционном сигнале
обязательно должна быть связь.
Пример 2: Реальная схема
Где ОП – обращённый
преобразователь
𝑘𝑘1 = 𝑘𝑘НОМ + ∆𝑘𝑘1
𝑘𝑘2 = 𝑘𝑘НОМ + ∆𝑘𝑘2
1
𝛽𝛽 =
𝑘𝑘НОМ
Хотим получить всегда:
𝑌𝑌 = 𝑘𝑘НОМ ∗ 𝑋𝑋 даже если ∆𝑘𝑘1 ≠ 0, ∆𝑘𝑘2 ≠ 0 при X=const
Случай А) П2 идеальный
𝑘𝑘2 = 𝑘𝑘НОМ
Тогда 𝑌𝑌 = 𝑘𝑘НОМ ∗ 𝑋𝑋 даже если ∆𝑘𝑘1 ≠ 0
Случай Б) П2 реальный
𝑘𝑘2 = 𝑘𝑘НОМ + ∆𝑘𝑘2
∆𝑘𝑘 ∗∆𝑘𝑘
Тогда 𝑌𝑌 = 𝑘𝑘НОМ ∗ 𝑋𝑋 − 1 2 ∗ 𝑋𝑋
𝑘𝑘НОМ
Ошибка второго порядка малости
43
18. Измерительне преобразователи. Классификация: по входным и
выходным величинам
1. ПАА - преобразователь аналоговой величины в аналоговую
Пример:
а) усилители
б) делитель
Все это масштабные преобразователи
2. АЦП - аналого-цифровой преобразователь
3. ЦАП – цифро-аналоговый преобразоваетль
4. ПКК – перобразователь кода в код
Под кодом в технике чаще всего подразумевается сигнал, построенный по
определенным правилам; набор цифр, построенный по определенным правилам.
Аналоговая величина характеризуется бесконечным числом значений на
определённом интервале. Дискретная – конечная величина; имеющая конечное число
значений. Код – совокупность правил, позволяющих передавать значения в виде
последовательности символов.
Пример:
ЦОУ – цифровое отсчётное устройство на светодиодах
Каждая черта – светодиод (всего – 8).
Масштабные преобразователи
- пассивные (а) (б)
- активные
(а) – делитель напряжения.
Предположим надо изменить напряжение на выходе относительно входа в кратное
число раз.
44
(а1) - делитель напряжения
+
uвых = uвх
R1
R2
- делитель напряжения
R1 + R2
UВХ=
R2
UВЫХ
-
(а2) - делитель напряжения с нагрузкой
R2 || RН
=
uвых u=
F ( RН )!!!
вх
R1 + R2 || RН
+
R1
UВХ=
R2
UВЫХ
Rн
-
(а3) – на входе синусоидальный сигнал
Пусть f= f1 ÷ f 2 - где f 2 - большая
На высоких частотах начинают сказываться паразитные
емкости.
+
R1
~
UВХ
R2
UВЫХ
-
ZC =
+
CП1
R1
КД =
~
UВХ
CП2
R2
-
1
j ⋅ 2π f ⋅ CП
R2 || X CП 2
R2 || X CП 2 + R1 || X CП 1
UВЫХ
(а4) Чаще всего используют компенсированные делители
КД ≠ F( f )
+
C1
~
UВХ
C2
-
UВЫХ
Но сказываются R потери
45
+
Rп1
C1
Rп2
C2
~
UВХ
UВЫХ
Rн
Часто нагрузку делают в виде емкости СН
+
C1
~
UВХ
C2
UВЫХ
Cн
-
Прибор (Масштабный преобразователь):
+
1
Переключатель
R1
2
R2
~
UВХ
(=)
3
R3
4
Rн
R4
5
R5
-
(б) – делители тока
5А-?
Ликбез
А
RН
1А
46
IA
Коэффициент
шунтирования
А
Iн
1
IA
=
n K=
Ш
5А
RШУНТ
RН
ИП
RШ1
R
RШ = A n −1
RШ2
I1
обычное имеет
малое
5А
сопротивление.
Шунты производятся многопредельными:
На примере (трёх предельный).
Общий
минус
Блок
питания
Kус
1А
UВЫХ
Насыщение
UВЫХ
3А
I3
I1>I2>I3
UВЫХ
Усилитель
I2
Пределы измерения (3-х предельная)
Активные масштабные преобразователи
- усилители
UВХ
RШ3
Насыщение
UДрейфа =var
UВХ
UВХ
АХ усилителя.
KУС =
U вых
U вх
Различают широкополосные и узкополосные усилители:
- широкополосный усилитель:
АЧХ
A
идеальная
A
АЧХ
0.707A
реальная
0.707A
A
Δf
Δf
Полоса пропускания
f
f
f=f0
Частота настройки
- узкополосный усилитель:
∆f f 0 (в Узкополосных усилителях)
f 0 - частота настройки.
47
19. Измерительные преобразователи. Первичные, вторичные.
Генераторные, параметрические
Измерительный преобразователь – это средство измерения, предназначенное для
выработки сигнала измеряемой информации в форме, позволяющей его передавать,
преобразовывать и т.д., НО недоступной для глаза наблюдателя.
На входе – различная физическая величина. На выходе – электрический сигнал на
передачу.
На входе может быть всё что угодно:
электрическая величина, магнитная,
химическая, неэлектрическая. На выходе
получаем такой электрический сигнал,
который можно регистрировать, передавать и т.д.
Здесь нет отсчётного устройства.
Основная характеристика прибора – функция Y = F(X). Это в идеале она однозначна, а
в реальности может быть и гистерезис (зависимость от двух переменных).
Если ИП разобрать, то внутри может оказаться несколько ИП, например первичный и
вторичный.
Обозначения:
ПИП – первичный ИП - это тот, что реагирует на входной сигнал. Обладает высокой
чувствительностью к измеряемой величине.
ВИП – вторичный – принимает первичный и преобразует его в электрический сигнал.
Измерительные преобразователи неэлектрических величин.
Такие устройства делятся на:
• Генераторные
Под действием X → Y – ЭДС или заряд
• Параметрические
Под действием X → Y меняет параметры: ΔR, ΔC, ΔL, ΔM, … Такие приборы требуют
внешнего источника питания.
Пример: генераторный
Пусть X – температура to . Берем термопару
E = k(tX – t0)
t0 – const = 00 – тающий лед
tx=var
Напряжение измеряем милливольтметром.
Пример: генераторный
48
Eфэ=Ψ
полупроводники):
Пример: параметрический
Рассмотрим термосопротивление (термисторы –
Для реализации должен быть источник питания
20. Преобразователи с унифицированным выходным сигналом
В последнее время всё чаще применяются измерительные преобразователи с
унифицированным выходным сигналом (ИПУВС).
К Y электрическому сигналу предъявляются определённые требования:
1. Вид сигнала:
• Может быть постоянным/переменным напряжением
• Током
• Частотой
• Фазой
• Может быть кодом
2. Зависимость выходной величины от входной должна быть линейна.
Y=f(X) – функция преобразования
3. Значения выходных параметров приводятся.
┌Максимальные значения – по току 100 мА; по
напряжению – 30 мВ.┘
Примечание:
Все ИПУВС выпускаются в определённом техническом оформлении.
49
На вход может подаваться, например: механическое воздействие, момент вращения,
давление, температура, концентрация, газ и прочее.
Обозначения:
ЧЭ – чувствительный элемент, основная задача – почувствовать малый входной
сигнал.
ПФВ – преобразователь физической величины.
МП – масштабный преобразователь, умеет увеличивать или уменьшать сигнал,
преобразовать сигнал в определённое число раз с высокой точностью. Классическим
представителем МП является шунт, делитель напряжений, усилитель, трансформатор.
ФП – функциональный преобразователь, задача: получить на выходе линейную
зависимость.
АЦП – аналого-цифровой преообразователь – аналоговую величину преобразует в
дискретуню (код).
ГР – гальваническая развязка – элемент, кторый обеспечивает повышение
помехозащищенности, чаще всего за счет разделения первичной и вторичной цепи
(очень часто применяются трансформаторы).
ЧЭ
Закон распределения может быть любой: возрастающий, падающий, линейный,
нелинейный.
Задача ЧЭ – на выходе получить реакцию, любую, но с хорошей точностью.
ПФВ
Задача – получить возрастающий закон, любой.
Существуют два вида помех:
1.
Нормальная (помеха нормального вида)
2.
Помеха общего вида
50
Существуют схемные (уменьшение проводов) и аппартатные методы избавдения от
помех.
В качестве гальванической развязки ставим трансформатор.
21. Аналого-цифровые преобразователи. Методы построения АЦП.
Квантование. Погрешность дискретности.
В задачах преобразования сигналов измерительной информации часто возникает
необходимость представления непрерывных сигналов дискретными и восстановления
непрерывного сигнала по его дискретным значениям. При этом непрерывный сигнал
y(t) представляется совокупностью дискретных значений y(t1), y(t2), y(t3), …, по
которым с помощью некоторого способа восстановления может быть получена оценка
y*(t) исходного сигнала y(t).
Процесс преобразования y(t) в y(t1), y(t2), y(t3), …, y(tn) называется дискретизацией
непрерывного сигнала. Наиболее часто применяется так называемая равномерная
дискретизация, при которой интервал между соседними отсчётами – шаг
дискретизации h = ti+1 - ti остаётся постоянным.
Процесс дискретизации сигнала сегодня проводится с помощью АЦП – аналогоцифровых преобразователей:
В основу преобразования непрерывной величины в дискретную положено квантование
по уровню.
Существует 3 метода квантования:
- отнесение к нижнему уровню
- отнесение к верхнему уровню
- отнесение к ближайшему уровню
51
1) Отнесение к нижнему уровню
Непрерывный сигнал квантуют по уровню (строят квантовую функцию)/
Эти уровни нумеруются с нуля, причём уровень с номером нуль – это уровень оси
абсцисс. На каждом уровне все значения равны (т.к. уровни - это параллельные
линии). Значит, если мы хотим узнать, что происходит на уровне N, используем
формулу 𝑁𝑁 ∗ ℎ.
h – шаг квантования (и разрешающая способность) = const.
Уровни квантования кодируются, т.е. переводятся в электрический сигнал.
Ошибка, то есть разность между аналоговой и квантованной функцией существует и
равна шагу квантования.
∆Хдискр = Хкв − Х
2) Отнесение к верхнему уровню
𝛥𝛥𝑋𝑋дискр−ти 𝑀𝑀𝑀𝑀𝑀𝑀 = −ℎ
𝛥𝛥𝑋𝑋дискр−ти 𝑀𝑀𝑀𝑀𝑀𝑀 = ℎ
3) Отнесение к ближнему уровню
Обратите внимание на минус в
погрешности для отнесения к
нижнему уровню и на плюс в
погрешности для отнесения к
верхнему уровню.
Погрешность можно уменьшить аж
до полушага квантования, если
провести квантованную функцию
по центру тяжести аналоговой
функции.
∆Хдискр = ±ℎ/2
1) Отнесение к нижнему уровню
2) Отнесение к верхнему уровню
52
3) Отнесение к ближнему уровню
Чтобы уменьшить погрешность надо уменьшать шаг квантования или увеличивать
число уровней квантования (а лучше и то и другое вместе).
Пример
Создать цифровой вольтметр с пределом 100 В. Погрешность 1%.
Сколько нужно уровней квантования и какая разрешающая способность?
100
Считаем 1%=1 В 𝑁𝑁 =
= 100 шт. => кол − во уровней = 100: 0 ÷ 99 => ℎ =
1
1В
В цифровом приборе с АЦП возникают динамические погрешности.
Динамические характеристики АЦП должны быть
связаны с временными характеристиками входного
сигнала.
┌Техническая реализация АЦП заключается в
следующем. АЦП строится на методе сравнения, где
сравнивается непрерывная величина с образцовой
величиной, построенной определённым образом, так
чтобы образцовая величина менялась дискретно.┘
Методы построения АЦП
1) Метод считывания
2) Метод последовательного счета
3) Метод сравнения вычитания – наиболее распространенный
Метод считывания
Идея:
Прибор определяет, к какому уровню квантования ближе сигнал.
┌При этом методе происходит одновременное сравнение измеряемой величины X с
известными величинами X1, X2, X3, …, значения которых равны уровням квантования.
Известная величина, равная измеряемой Xi = X(tИ), даёт номер отождествляемого
уровня квантования, в соответствии с которым образуется код, то есть значение
измеряемой величины.┘
Технический шаблон
53
Метод последовательного счета
(Времяимпульсный вольтметр)
Сигнал определяется по количеству
ступеней (h=const)
┌При этом методе происходит
последовательное во времени сравнение
измеряемой величины X с известной
величиной Xi (ступенька),
изменяющейся (возрастающей или
убывающей) во времени скачками,
причём каждый скачок соответствует шагу (ступени) квантования h по уровню. Число
ступеней, при котором наступает равенство X = Xi(tИ) (c некоторой погрешностью),
равно номеру отождествляемого уровня квантования. В процессе сравнения
образуется код, соответствующий номеру отождествляемого уровня квантования.
Возможно инверсное преобразование, при котором известная постоянная величина
сравнивается с равномерно квантуемой величиной, функционально связанной с
измеряемой величиной.┘
Метод сравнения вычитания
Квантованную функцию строят по определенному алгоритму в соответствии с кодом.
┌При этом методе происходит
последовательное во времени сравнение
измеряемой величины X c известной
квантованной величиной Xi ,
изменяющейся во времени скачками по
определённому правилу (исключая
единичную систему счисления). Значение
известной величины при которой наступает
равенство X = Xi(tИ), соответствует номеру
отождествляемого уровня квантования.
Код, образуемый в процессе этой операции, соответствует отождествляемому
уровню.┘
Пример для Метода сравнения вычитания
Пусть Uвх=100 В
А по коду 2 – 4 – 2 – 1
ИОН – источник образцового напряжения
Очень точный. Работает на нагрузку (Ri и Ri* - высокоточные)
СУ – сравнивающее устройство
54
УУ – устройство
управления
Если все ключи
разомкнуты: Umax=99.9
B
Если все ключи
замкнуты: Umin=0 В
Чтобы при включении ток был постоянным при
любых переключениях Ri, нам нужны Ri*.
Работа схемы:
Пусть на вход подается 100 В. Пусть исходное
Uкв=99,9 В (все ключи Кi замкнуты) => UАЦП=0 (все
ключи Ki* разомкнуты).
Пусть Uкв=0 В и Uвх=73,3 В
СУ= Uвх- UАЦП.
22. Классификация измерительных приборов с краткой характеристикой
(показывающие, регистирующие, регулирующие, электромеханические,
электронные, цифровые, аналого-дискретные)
По дополнительным функциям:
1. Показывающие
2. Регистрирующие
3. Регулирующие
Показывающие только измеряют и показывают (амперметр, вольтметр и т.д.).
Регистрирующие измеряют и регистрируют (фиксируют) результат.
На чём фиксируют? Например:
1) на Бумаге (визуальный сигнал), например, перо, чернила
2) на Фотоплёнке (визуальный сигнал), например, свет
3) на Магнитной ленте (невизуальный сигнал; информация требует
воспроизведения (как на магнитофоне))
4) на Экране ЭЛТ (визуальный сигнал), например, аналоговый прибор
5) на Цифровом дисплее (визуальный сигнал)!!!
Самая высокая плотность записи информации – на магнитной ленте.
Примеры регистрирующих приборов:
Самопишущий прибор – аналоговый прибор, который позволяет зафиксировать на
бумаге один или несколько сигналов во времени.
Самый простой самопишущий прибор:
55
Такие самописцы позволяют
регистрировать сигналы очень низкой
частоты (доли Гц – Гц).
Есть до 100 Гц, но сделать трудно.
Дополнительный пример 1:
Чтобы узнать ∆Uост, заворачиваем вход
∆Uост – остаточное напряжение, оно
непостоянно, зависит от температуры,
времени, источника питания.
Дополнительный пример 2:
Прямая, если x=const
Существуют самопишущие приборы для фиксации
функциональной зависимости.
56
Двухкоординатные самописцы
Y = f(X)
Примечание: Все самопишущие приборы разделяются по частоте.
Самый точный – электронный цифровой осциллограф.
Регулирующие средства измерения – показывают, регистрируют, что-то регулируют
(могут что-то включать, отключать, подавать сигнал). Им присуща функция
управления.
Регулирующие средства измерения бывают:
а. измерительные
б. управляющие чем-то
Пример:
b
a
a=b
Узкопрофильные: b<<a
1) Однопозиционное регулирование
I=0÷4 А - норма
I>4 А - авария, нужно что-то отключить
2) Двупозиционное регулирование
2 А<I<4 A - норма
I<2 A и I>4 A - авария
57
ЭЛЕКТРОМЕХАНИЧЕСКИЕ ПРИБОРЫ 𝑋𝑋? → 𝑊𝑊Э → 𝑊𝑊МЕХ →𝑋𝑋𝛼𝛼ПЕР → 𝑋𝑋П
Под действием измеряемой величины возникает электрическая энергия, которая
преобразуется в механическую энергию поворота подвижной части (стрелки,
например). В результате получается угол поворота α или, реже, длина линейного
перемещения XПЕР. В результате получается показания XП.
Обозначения: ИЦ – измерительная цепь; PИЦ – параметры измерительной цепи, ИМ –
измерительный механизм; PИМ – параметры измерительного механизма, ОУ –
отсчетное устройство; PОУ – параметры отсчётного устройства.
Чаще всего α = 900, иногда = 1350, очень редко = 30 – высокочувстивтельные приборы.
ИЦ-ами чаще всего являются делители напряжений, шунты и т.д.В идеале
зависимость показаний и измеряемой величины должна быть такая XП = F(X), т.е.
однозначная зависимость. А на деле всё оказывается совсем по-другому XП = F(X, PИЦ
, PИМ, PОУ) Разумеется при Pij = var, то появляется погрешность. Что можно сделать,
чтобы этого избежать: Зафиксировать параметры Pij = const, что очень трудно,
Оставить параметры в покое Pij = var, но ввести схемы компенсации (от частоты, от
температуры, от внешнего напряжения). Электромеханические приборы не требуют
внешнего источника питания, питаясь от самой измеряемой величины, подаваемой на
вход. Они простые, дешевые, незатратные, и т.д.
α= F(X) – характеристика шкалы.
XП = F*(α) – градуировочная характеристика.
┌Электронные приборы:
ЭС – электрическая схема, ППИ – переключатель пределов измерения, СК, СУН –
схема калибровки, схема установки нуля, БП – блок питания, ОУ – отсчётное
устройство. Приборы универсальны, измеряют все величины; имеют широкий
диапазон частот. Для электронного прибора сопротивление входа стремится к
бесконечности (проще говоря, составляет мегаомы).
58
Цифровой прибор
П – преобразователь (входная величина X – всё что угодно), АЦП – аналого-цифровой
преобразователь, ЦОУ - цифровое отсчётное устройство. Десятичное число –
трёхразрядное. Э – экран
Достоинства: универсальность, высокая точность, возможность вывода на экран ЭВМ.
Аналого-дискретные приборы - Прибор с газоразрядным самосканирующим
отсчётным устройством (ГРСОУ).
Надо, чтобы l = UX, где l – длина света газоразрядной трубки, ГЛИН – генератор
линейно изменяющегося напряжения, ДЧ – датчик частоты, УУ – устройство
управления, KA – ключ анода, KI,II,III- управляющие ключи (управляются от УУ),
которые объединяютсяв группы I – 1,4,7; II – 2,5,8; III – 3,6,9. Есть еще K0 – ключ
отвечает за катод.
Ключи переключаются много раз, для этого и необходим ДЧ.
Работа схемы:
1) Все ключи разомкнуты
59
2) 1 такт: K0 замкнут, остальные разомкнуты
3) 2 такт: K0 – разомкнут, KI – замкнут, остальные разомкнуты и т.д.
Если мы хотим остановить ключ на какой-то отметке, нужно остановить анодное
напряжение KA (замкнуть). Анодое напряжениеуменьшается и разряд прекращается.
23. Типы отсчетных устройств в измирительных приборах
Не всегда отсчетное устройство позволяет считать саму измеряемую величину.
Бывают отсчетные устройства со шкалой, проградуированной иной величиной, но
показания позволяют найти саму необходимую величину.
а) АНАЛОГОВЫЙ СТРЕЛОЧНЫЙ ОТСЧЁТ Градуированная шкала + стрелка (указатель).
Для электронных и электромеханических приборов. Такие отсчётные устройства
менее чувствительны.
б) АНАЛОГОВЫЙ СВЕТОВОЙ ОТСЧЁТ - это означает градуированная шкала + «заяц»
(световое пятно).
Для электромеханических приборов. Такие системы более чувствительны.
в) ЦИФРОВОЙ ОТСЧЁТ
Результат видим в десятичной системе исчисления в виде цифр, появляющихся на
экране или мониторе. Используется, естественно, в цифровых
приборах.
Недостоверным является последний разряд.
3,85 В
60
В данном случае «пятёрка» будет недостоверна.
г) ЦИФРО-АНАЛОГОВЫЙ ОТСЧЁТ
Они сохраняют преимущества аналогового (непрерывного) отсчёта и достоинства
цифрового (точность, возможность использования машины).
Пример
В таких приборах шкалы и указатели (отсчётные устройства) делаются на новых
физических эффектах, когда под действием измеряемой величины индикаторное
вещество меняет свои оптические свойства, граница эффекта и является указателем.
24. Метрологические характеристики средств измерения в статическом
режиме
Характеристики средств измерений делятся на:
1) метрологические (влияющие на точность измерений);
2) неметрологические (не влияющие на точность измерений);
Статический режим – это когда измеряемая величина не меняется во времени и все
переходные процессы закончены.
1. Погрешность СИ – это отклонение результата измерений от истинного значения
измеряемой величины.
Она может быть в абсолютных величинах и относительных (в частности в процентах).
Истинное значение найдено быть не может, т.к. любое средство измерений обладает
погрешностью. Всё в природе непрерывно изменяется.
При определении погрешности используют вместо истинного - действительное
значение.
Действительное значение – значение физической величины, найденное
экспериментальным путём и настолько приближается к истинному, что для данной
цели может быть принято вместо него.
Никогда не находим настоящую погрешность, всегда находим оценку.
Иногда в показания характеристики средств измерений пользуются термином
точность, под которым понимается степень приближения результатов измерения к
действительному (к истинному) значению измеряемой величины, т.е. качество СИ,
отражающие близость к «0» его погрешностей.
В зависимости от изменения во времени измеряемой величины различают:
1) Статистические погрешности - погрешности при изменении постоянной во времени
величины.
2) Динамические погрешности - разность между погрешностью в динамическом режиме
и статистической погрешностью.
В зависимости от условий возникновения различают:
1. Основная погрешность - погрешность СИ при нормальных условиях работы.
61
2. Дополнительная погрешность - погрешность СИ, вызвана отступление от нормальных
условий одного из влияющих факторов.
Если в паспорте средств измерений написано, что прибор работает при 20°С, он
никогда работать не будет.
В зависимости от характера изменения погрешности:
1) Систематические погрешности - погрешности постоянные или закономерно
изменяющиеся, т.е. закон изменения известен.
2) Случайные погрешности - погрешности, изменяющиеся случайным образом, т.е. закон
изменения остаётся не известным.
В зависимости по применяемой формуле:
1. Абсолютная погрешность – разность между результатом измерения и истинным
значением измеряемой величины.
∆ = x - 𝑥𝑥и = x - 𝑥𝑥Д
При конкретном определении погрешности ∆ имеет знак и обязательно имеет
размерность измеряемой величины.
2. Относительная погрешность – отношение абсолютной погрешности к значению
измеряемой величины. Обычно выражается в [%].
δ=(∆/x) *100%
δ будет иметь знак
3. Приведённая погрешность – отношение абсолютной погрешности к
нормированному значению [%]
∆
γ= *100% , где 𝑥𝑥𝑁𝑁 - нормированное значение
𝑥𝑥𝑁𝑁
В зависимости от изменения измеряемой величины:
1) Аддитивная (погрешность нуля) - это те погрешности, которые не зависят от
измеряемой величины.
Пример: дрейф нуля у усилителя постоянного тока (УПТ).
Никакая величина на может идти идеально строго, она колеблется возле своего
значения.
X =0, y≠0
2) Мультипликативная (погрешность коэффициента отклонения) – это те погрешности,
которые зависят от измеряемой величины.
62
∆М = ± 𝛾𝛾𝑆𝑆 ∗ 𝑋𝑋
вот это (обведённое) – погрешность чувствительности
Примером может случить
непостоянство коэффициента усиления
у усилителя постоянного и
переменного токов.
𝑈𝑈
𝐾𝐾УС = ВЫХ
𝑈𝑈ВХ
𝛿𝛿 =
∆
𝑋𝑋ДЕЙСТВ
∆
∆
𝛾𝛾 ∗𝑋𝑋
𝐾𝐾УС = 𝐾𝐾НОМ ± ∆𝐾𝐾УС
В общем случае полная погрешность
складывается из:
∆= ∆АД + ∆М = ∆АД + 𝛾𝛾𝑆𝑆 ∗ 𝑋𝑋
∗ 100% = � АД + 𝑆𝑆 � ∗ 100% = � АД + 𝛾𝛾𝑆𝑆 � ∗ 100%
𝑋𝑋
𝑋𝑋
𝑋𝑋
2. Вариация выходного
сигнала или показания прибора
Вариация – разность между значениями информативного параметра выходного
сигнала или показания прибора, соответствующему данной точке диапазона
измерений при двух направлениях медленных изменений информативного параметра
входного сигнала в процессе подхода к данной точке диапазона измерений.
Информативный параметр сигнала – параметр, функционально связанный с
измеренным свойством или являющийся самим измеряемым свойством объекта
измерений.
Неинформативный параметр сигнала - параметр, функционально несвязанный с
измеренным свойством.
Пример:
U(t) = 𝑈𝑈𝑚𝑚 sin(ωt -φ) – три параметра.
63
Одна из причин вариации – трение в электромеханических приборах (опорах).
3. Чувствительность СИ – производная от выходной величины по входной измеряемой
величине.
𝑑𝑑𝑑𝑑
S=
𝑑𝑑𝑑𝑑
Чувствительность всегда имеет размерность.
Чувствительность к току, напряжению, мощности и т.д
Для приборов существует понятие постоянная прибора.
1
С=
𝑆𝑆
Постоянна по …
Порог чувствительности – наименьшее значение измеренной величины, способное
вызвать заметное изменение выходного сигнала СИ.
Размерность порога – размерность измеряемой величины.
4. Диапазон измерений – область значений измеряемой величины, для которой
нормированы допускаемые погрешности СИ.
Нормированы (заданы, определены).
С целью повышения точности измерений диапазон
измерений средства измерения может быть разбит на
несколько поддиапазонов. При переходе с одного
поддиапазона на другой некоторые составляющие основной
погрешности (погрешность в условиях, принятых за
нормальные для данного средства) уменьшаются, что
приводит к повышению точности измерений. При нормировании допускают для
каждого поддиапазона свои предельные погрешности.
┌Диапазон показаний – где может находится стрелка. Или, если по-научному, это
область значений шкалы, ограниченная начальным и конечным значением шкалы
прибора.
Динамический диапазон – отношение максимально возможного значения к
минимально возможному.
𝑋𝑋𝑀𝑀𝑀𝑀𝑀𝑀
𝐷𝐷ДИН =
𝑋𝑋𝑀𝑀𝑀𝑀𝑀𝑀
Используется только для многопредельных приборов. ┘
5. Входной импеданс СИ – характеристика, определяющая реакцию входного сигнала
на подключение СИ к источнику входного сигнала с фиксированным выходным
импедансом.
(Влияние СИ на объект).
Выходной импеданс – характеристика средств измерений,
определяющая реакцию его выходного сигнала, на
подключение к его выходу фиксированной нагрузки.
64
6. Надёжность СИ – способность сохранять заданные характеристики при
определённых условиях работы в течении заданного времени.
λ- интенсивность отказов (число отказов в ед. времени).
1 область – участок приработки.
2 - участок нормальной работы.
3 - участок старения.
┌
7. Функция преобразования или передаточная характеристика (ПХ)
𝑌𝑌 = 𝐹𝐹(𝑋𝑋)
Это всегда зависимость выходной величины от входной. Функция F может быть как
линейной, так и нелинейной. Но, стремятся получить именно линейную функцию,
кроме особых случаев.
8. Функция влияния
Таким образом 𝑌𝑌 = 𝐹𝐹(𝑋𝑋, 𝜉𝜉1 , 𝜉𝜉2 , 𝜉𝜉3 ) , что плохо, так как мы всегда добиваемся
однозначного соответствия «игрэк – икс».
𝜕𝜕𝜕𝜕
𝜕𝜕𝜕𝜕
𝜕𝜕𝜕𝜕
𝜕𝜕𝜕𝜕
∗ ∆𝑋𝑋 +
∗ ∆𝜉𝜉1 +
∗ ∆𝜉𝜉2 +
∗ ∆𝜉𝜉3
𝜕𝜕𝜕𝜕
𝜕𝜕𝜉𝜉1
𝜕𝜕𝜉𝜉2
𝜕𝜕𝜉𝜉3
Основная
Дополнительные
погрешность
погрешности
𝜕𝜕𝜕𝜕
- это коэффициент влияния, а
∗ ∆𝜉𝜉1 - это функция влияния
∆𝑌𝑌 =
где
𝜕𝜕𝜕𝜕
𝜕𝜕𝜉𝜉1
Пример:
Пусть ξ = 30 ÷ 50 o Тогда Δξ = + 20 о
𝜕𝜕𝜉𝜉1
25. Динамический режим. Динамические характеристики средств
измерений
Динамический режим возникает, если:
•
Сигнал меняется во времени
•
Нагрузка меняется во времени
•
Влияющие факторы меняются во времени
Динамика проявляется в двух ипостасях:
•
Запаздывание выходного сигнала по отношению к входному
65
•
Возможное искажение выходного сигнала относительно входного
В общем виде эта задача по определению полной динамики средства измерения
решается.
Для решения, необходимо записать дифференциальное уравнение (ДУ):
𝑚𝑚
𝑚𝑚
𝑑𝑑 𝑖𝑖 𝑦𝑦
𝑑𝑑 𝑗𝑗 𝑦𝑦
� 𝐴𝐴𝑖𝑖 ∗ 𝑖𝑖 = � 𝐵𝐵𝑗𝑗 ∗
𝑑𝑑𝑑𝑑
𝑑𝑑 𝑡𝑡 𝑗𝑗
𝑖𝑖=1
𝑗𝑗=1
где А и В – параметры сигнала и параметры устройства.
В большинстве случаев нет необходимости решать ДУ I порядка, достаточно
решить ДУ II порядка.
Для динамики очень важен вид входного воздействия. Когда говорим о
динамических характеристиках необходимо указывается вид входного воздействия.
Различают:
• Полные динамические характеристики
• Частные динамические характеристики
Среди полных динамических характеристик, в свою очередь, различают
следующие:
1) Переходная функция (характеристика)
Если входной сигнал изменился скачком (произошёл «толчок»), то выходной
сигнал изменится по переходной характеристике. Проще говоря - ПХ - это реакция на
воздействие вида единичной ступенчатой функции (ЕСФ).
2) Импульсная характеристика
Это реакция на воздействие вида ЕИФ (единичная импульсная функция), то есть
такого воздействия, которое равно бесконечности в точке t = t0 и равна нулю при всех
остальных значениях времени.
3) Передаточная функция (ПФ)
𝑌𝑌(𝑠𝑠) 𝑓𝑓ВЫХ (𝑠𝑠)
=
𝑋𝑋(𝑠𝑠)
𝑓𝑓ВХ (𝑠𝑠)
Это отношение преобразованного по Лапласу выходного сигнала к
преобразованному по Лапласу входному сигналу при нулевых начальных условиях
(ННУ).
4) Амплитудно-фазовая характеристика [или частотная характеристика (ЧХ)]
𝐻𝐻(𝑠𝑠) =
66
𝑌𝑌(𝑗𝑗𝑗𝑗) 𝑓𝑓ВЫХ (𝑗𝑗𝑗𝑗)
=
𝑋𝑋(𝑗𝑗𝑗𝑗)
𝑓𝑓ВХ (𝑗𝑗𝑗𝑗)
Это отношение преобразованного по Фурье выходного сигнала
преобразованному по Фурье входному при нулевых начальных условиях (ННУ).
𝐻𝐻(𝑗𝑗𝑗𝑗) =
АФХ (ЧХ) имеет две составляющие
к
АЧХ (амплитудно-частотная характеристика)
ФЧХ (фазо-частотная характеристика)
АЧХ говорит о возможных искажениях выходного сигнала по отношению к
входному.
ФЧХ говорит о запаздывании выходного сигнала по отношению к входному.
|𝑓𝑓ВЫХ (𝑗𝑗𝑗𝑗)|
АЧХ 𝐴𝐴(𝜔𝜔) = |𝐻𝐻(𝑗𝑗𝑗𝑗)| =
|𝑓𝑓ВХ (𝑗𝑗𝑗𝑗)|
ФЧХ 𝛷𝛷(𝜔𝜔) = 𝑎𝑎𝑎𝑎𝑎𝑎{𝐻𝐻(𝑗𝑗𝑗𝑗)} = 𝑎𝑎𝑎𝑎𝑎𝑎{𝑓𝑓ВЫХ (𝑗𝑗𝑗𝑗)} − 𝑎𝑎𝑎𝑎𝑎𝑎{𝑓𝑓ВХ (𝑗𝑗𝑗𝑗)}
Пример:
АЧХ
(1)
𝜏𝜏 = 𝜔𝜔0 ∗ 𝑡𝑡
𝑑𝑑 2 𝑦𝑦
𝑑𝑑𝜏𝜏
и
+ 2 ∗ 𝛽𝛽 ∗
2
𝑞𝑞 =
𝜔𝜔
𝜔𝜔0
𝑑𝑑𝑑𝑑
𝑑𝑑𝑑𝑑
+ 𝑦𝑦 = sin(𝑞𝑞 ∗ 𝜏𝜏), где
, причём
𝝎𝝎 – частота возмущения, 𝝎𝝎0 – собственная частота средства измерения
𝜷𝜷 - степень успокоения (зависит от параметров устройства и нагрузки)
В правой части уравнения (1) стоит синусоидальное возмущение, в левой – ДУ
второго порядка.
Решение ДУ второго порядка складывается из общего решения (решения ДУ при
приравненной к нулю правой части) (как процесс идёт во времени) и частного решения
(отклик на возмущение).
Частное решение или отклик на возмущение:
𝑌𝑌 = 𝑋𝑋 ∙ sin(𝑞𝑞 ∙ 𝜏𝜏 − 𝜑𝜑), причём
X – амплитуда отклика
𝛗𝛗 – запаздывание отклика по отношению к возмущению
2 ∙ 𝛽𝛽 ∙ 𝑞𝑞
𝜑𝜑 = 𝑎𝑎𝑎𝑎𝑎𝑎𝑎𝑎𝑎𝑎 �
�
1 − 𝑞𝑞 2
1
𝑋𝑋 =
�(1 − 𝑞𝑞 2 )2 + 4 ∙ 𝛽𝛽 2 ∙ 𝑞𝑞 2
Утверждаем, что
𝜔𝜔
𝑋𝑋 = 𝐹𝐹1 � , 𝛽𝛽�
𝜔𝜔0
Тогда, можно смело сказать, что
𝜔𝜔
𝜑𝜑 = 𝐹𝐹2 � , 𝛽𝛽�
𝜔𝜔0
Тогда, строим АЧХ
67
Из графика видно:
• При q = 0, 𝝎𝝎 << 𝝎𝝎0 Искажений естественно нет, ибо АЧХ(0) = 1.
• При q >> 1, 𝝎𝝎 >> 𝝎𝝎0 Сигнал не проходит вовсе.
• При q = 1, 𝝎𝝎 = 𝝎𝝎0 Происходит резонанс.
• При степени успокоения 𝜷𝜷=0.707 в большом диапазоне частот
характеристика параллельна, т.е. входной сигнал не искажается и АЧХ
приближается к идеальному:
Рассмотрим, как ведёт себя устройство с такой
АЧХ при различных
видах входного воздействия.
Пример: Берём характеристику при степени успокоения 𝜷𝜷=0.707
А) Пусть 𝝎𝝎 = 𝝎𝝎1, а сигнал – частая синусоида.
68
На выход пойдёт всё ещё синусоида, но с меньшей амплитудой.
Разъясняем: у синусоиды, из-за её пологой формы, спектр будет не сильно
широким и будет целиком укладываться в полосу пропускания. Следовательно –
искажений по форме – нет. Но так как частота 𝝎𝝎1 находится уже за пределом
параллельной части АЧХ, следовательно, будем иметь искажения по амплитуде, так как
коэффициент передачи будет меньше единицы.
Таким образом:
Б) Пусть 𝝎𝝎 = 𝝎𝝎2, а сигнал – меандр.
Спектр такого сигнала бесконечен (по правилу: чем круче сигнал, тем шире его
спектр). Пропустить мы должны все гармоники такого сигнала, коих бесконечно много.
Тогда, гармоника номер N будет очень далеко уходить в бесконечность по оси (q =
𝝎𝝎/𝝎𝝎0). Тогда гармоника номер N, N+1, N+2 и так далее будут давать искажения
выходного сигнала относительно входного. А за счёт того, что 𝝎𝝎2 всё ещё находится в
параллельной части АЧХ, сигнал не изменится по амплитуде.
Таким образом:
Частные характеристики:
• 𝝎𝝎0 – собственная частота
• Коэффициент успокоения Р (или степень успокоения 𝜷𝜷)
• Время установления показаний
Пример: К успокоению…
69
КУ – коэффициент успокоения
Разумеется, три ампера стрелка «находит» не сразу. Выглядит этот процесс
следующим образом:
Критический режим является наилучшим. Это естественно, ведь при нём искомое
значение достигается быстрее, чем при работе в остальных режимах. Но, к сожалению
не все приборы работают в критическом режиме измерения показаний. Для них и
введено следующее:
Определение
Время установления показания – промежуток времени с момента изменения
измеряемой величины до того момента, когда указатель не будет выходить из
определённой зоны, устанавливаемой по нормативам (ГОСТу).
Пример:
1%).
Зоной допуска обычно является один процент от длины шкалы прибора (т.е. XП ±
70
Пример:
Для шкалы на 5 делений, зона допуска будет (±0,05).
Для шкалы в 30 делений, зона допуска будет (±0,3).
И так далее…
У электромеханических приборов время установления показаний (tУСТ) должно
быть менее 4 секунд.
У цифровых приборов tУСТ измеряется не временем, а числом показаний в секунду
(у современных – 107 штук в секунду).
26. Нормирование метрологических средств измерений.
Нормирование – это установление номинальных значений характеристик и зоны
разрешённого разброса с гарантированной точностью.
Характеристики, подлежащие нормированию:
1) Нормируют все характеристики, с помощью которых определяется результат
измерений
(функция преобразования, цена деления и т.д.)
2) Нормируют, как средства измерений реагируют на влияющие факторы
(чувствительность
приборов)
3) Погрешности
4) Характеристики, характеризующие влияние на средства измерений нагрузки
(входной и
выходной импульс)
5) Динамические характеристики
6) Информативные и неинформативные параметры (см. в преобразователях)
Пример: Пусть 𝑌𝑌 = 𝑋𝑋 ∙ sin(𝜔𝜔 ∙ 𝑡𝑡 − 𝜑𝜑)
Если 𝑋𝑋 = 𝐹𝐹(𝑌𝑌), то X – информативный параметр и должен нормироваться, а 𝝎𝝎 и 𝛗𝛗 –
неинформативные, но всё равно должны нормироваться.
27. Нормирование погрешности средств измерений. Класс точности
Погрешности могут выражаться в виде:
1. Абсолютных
2. Относительных
3. Приведённых
4. Числа деления шкалы
1. Абсолютная погрешность
Нормирование – предел допускаемой
абсолютной погрешности выражается:
А) ∆=±а (с одним значением)
Б) линейной зависимостью ∆=±( а +bх)
а – постоянная величина, имеющая размерность
измеренной величины
б – постоянное число, не имеет размерности
Нормирование по пункту а) осуществляется в случае, если нет мультипликативной
погрешности или она не учитывается.
Если ∆ мала или устраивает нас, то ее не учитываем.
71
Недостатком нормирования по абсолютной погрешности является невозможность
сравнения по точности СИ различного назначения, а также СИ с резко
отличающимися диапазонами.
Пример: 1А≠1В
2. Относительная погрешность
Нормирование:
Если нет мультипликативной погрешности или она не учитывается:
А) δ=±С, где С –постоянное число в %
𝑥𝑥
Б) ) δ=±[c+d( 𝑘𝑘 -1)]
𝑥𝑥
C,d – постоянные числа в %
𝑥𝑥𝑘𝑘 – конечное значение диапазона измерений
X – значение измеряемой величины
𝑥𝑥𝑘𝑘 и x берутся без знака.
Недостатком нормирования по относительной погрешности является то, что при x→0
δ→∞, т.е. сравнение СИ по точности оказывается затруднительным, некорректным.
3. Приведённая погрешность
Нормирование по приведённой погрешности только при отсутствии
мультипликативной погрешности или она незначительна.
𝑥𝑥𝑁𝑁 выбирается равным в зависимости от вида шкалы:
a) Для СИ, у которых нулевая отметка находится на краю или вне шкалы:
𝑥𝑥𝑁𝑁 = конечное значение диапазона измерений.
Б) для СИ , у которых нулевая отметка находится внутри диапазона измерений, 𝑥𝑥𝑁𝑁
равно арифметической сумме конечных значений диапазона измерений. 𝑥𝑥𝑁𝑁 = |𝑎𝑎𝑚𝑚 |+|𝑎𝑎𝑛𝑛 |
В) для СИ, предназначенных для измерения номинального значений, 𝑥𝑥𝑁𝑁 равно этому
номинальному значению.
Пример: прибор для измерения частоты в сети:
𝑥𝑥𝑁𝑁 = 50 Гц
Обобщённой метрологической характеристикой СИ является класс точности,
который определяет допускаемые пределы всех погрешностей (основные,
дополнительные и т.д.), а также все другие свойства влияющие на точность СИ.
Для СИ, пределы допускаемых погрешностей выражают в виде относительных или
приведённых погрешностей, т.е. в %, установлен ряд чисел для выражения предела
допускаемых погрешностей и применяемых для обозначения класса точности.
(1, 1.5, 2, 2.5, 4, 6)10n , где n=1, 0, -1, -2, -3, …
Пример: класс точности прибора 1,1%, но такого в списке нет, поэтому для этого
прибора класс точности 1,5%.
72
Для СИ, у которых основную погрешность нормируют в виде приведённой
погрешности, класс точности численно равен этому пределу, т.е. γ.
Если предел допускаемой основной погрешности определяется в виде относительной
погрешности по двучленной формуле, то в обозначении класса точности вводятся
числа c/d (/ - это не деление).
┌c/d; γ; δ – из ряда┘.
Правило записи результата с погрешностью
1. Погрешность (любая) не более двух значащих цифр.
Пример:
∆=7457 Ом → 7500 Ом = 7,5 кОм
2. Последний разряд погрешности и последний разряд результата должны
соответствовать друг другу.
Примеры задачи на экзамене
Пример 1:
Вольтметр, класс точности 0,5. С какой точностью измерено 100 вольт?
(Если класс задан в виде одного числа без дополнительных указаний, то это
приведенная погрешность).
∆
γ= *100% γ=0,5
𝑥𝑥𝑁𝑁
∆=1,5 в
Результат: U=100,0±1,5 в
Пример 2:
Пример для цифрового ваттметра:
Если класс точности по δ, то
δ=0,5
δ=(∆/x)*100%
∆=(δ∆/100)=(0.5*100)/100=0.5 Вт
P=100.0±0.5 Вт
Пример 3:
Пример для цифрового вольтметра:
Класс точности задан в виде c/d:
c/d=0.5/0.2
δ=±[0,5+0,2*(300/100-1)]=±0.9%
73
Ux = 100,0±0,9 В
28. Общие сведения о погрешности измерений. Причины появления
погрешностей. Классификация
Так как получить истинные данные об объекте в принципе невозможно, для любых
измерений характерна погрешность ΔX:
∆𝑋𝑋 = 𝑋𝑋измер − 𝑋𝑋ист = 𝑋𝑋измер − 𝑋𝑋д ,
где XИЗМЕР – расчётное значение измеряемой величины (искомой величины), а ХИСТ –
истинное значение (то, что есть на самом деле), ХД – действительное значение
измеряемой величины (которое близко к истинному).
Иными словами, погрешность – это разница между измеренным и истинным значением.
Как уже было говорено (причем, неоднократно) погрешности возникают при любых
измерениях и наблюдениях. Представим себе: ИЗМЕРИТЕЛЬНЫЙ ЭКСПЕРИМЕНТ.
Причины появления погрешности
1. Инструментальная погрешность
Погрешность самого прибора
Определяется классом точности прибора К и по ∆𝑀𝑀𝑀𝑀𝑀𝑀 ; 𝛿𝛿𝑀𝑀𝑀𝑀𝑀𝑀 ; 𝛾𝛾𝑀𝑀𝑀𝑀𝑀𝑀 .
2. Методические
а) несоответствие модели и объекта
Пусть объект измерения – генератор.
74
Подключаем генератор, естественно, к вольтметру…
А нам необходимо было максимальное напряжение UMAX, которое равно:
𝑈𝑈𝑀𝑀𝑀𝑀𝑀𝑀 = U ∗ 𝐾𝐾,
где К – тот неизвестный коэффициент, при увеличении на который напряжение выдает
нам «U-максимальное».
И вот тут встаёт проблема выбора дальнейшей модели:
- если напряжение – в синусоидальном режиме (как мы предположили в самом начале),
то коэффициент К = √2, как известно из курса электрических цепей.
- если же напряжение не в синусоидальном режиме, то и коэффициент, соответственно,
не √2, а что-нибудь другое.
б) Измеряемая величина – ток
Большой
Маленький
методы измерения разные
Очень маленький
в) Методическая погрешность преобразования аналоговой величины в цифровую
Ошибка, то есть разность между
аналоговой и квантованной функцией
существует и равна шагу квантования.
3.
Личные особенности
экспериментатора и его состояние
Экспериментирующий может
совершать промахи (грубые погрешности, которые на первой же стадии обработки
изымаются из протокола наблюдений) или просто произвести неправильный «отсчет
шкалы» прибора.
4. Вычислительные погрешности, связанные с особенностями ЭВМ и
особенностями принимаемых алгоритмов расчёта
5. Погрешности, связанные с влияющими факторами (как то: температура, частота,
влажность, давление и проч.)
а) постоянные или меняющиеся по определённому закону (получше)
б) случайные (пострашнее)
75
29. Погрешности систематические и случайные. Описание случайных
погрешностей. Понятие доверительного интервала погрешности
∆𝑋𝑋 = ∆СИСТ. + ∆СЛУЧ. = ∆СИСТ. + 𝛿𝛿̇
Оба этих вида погрешностей формируются под воздействием ряда факторов:
1) Систематические погрешности формируются под воздействием постоянных
факторов или факторов, меняющихся по определённому закону. Тогда, можем
утверждать, что систематическая погрешность остаётся постоянной (или меняется по
определённому закону) при многократных измерениях одной и той же случайной
величины.
2) Если эти факторы меняются случайным образом и их интенсивность трудно
предсказать, то это случайные погрешности.
Случайные же погрешности уменьшить нельзя, их можно лишь учесть методами
математической статистики. От случайной погрешности избавиться нельзя.
Измерение можно назвать правильным тогда, когда ∆СИСТ. → ∆𝑀𝑀𝑀𝑀𝑀𝑀 → 0
то есть систематические погрешности сведены к минимуму (в идеале – к нулю). Если
систематические погрешности остаются, то их чаще всего будут учитывать в виде
случайных погрешностей.
Пример 1: Здесь систематическая погрешность остаётся постоянной.
76
𝑅𝑅0 = 𝑅𝑅НОМ ± ∆𝑅𝑅 =например=100 ± 0,1 Ом
Пример 2: Здесь погрешность меняется по определённому закону.
Пример 3: Из жизни «Кувалда»
Систематические погрешности, как уже было сказано, необходимо уменьшить. Как
это можно сделать? А, например, вот так:
Правильно поставить эксперимент (чтобы никаких помех и шумов при измерениях,
чтобы никаких магнитов рядом не было, чтобы никто не отвлекал от снятия
результатов и так далее)
Эксперимент
А в это время в лабораторию, скажем, внесли
постоянный магнит и «испортили» вам результаты.
То, что мы не можем или просто позабыли соблюсти
относится к случайным погрешностям.
Систематические погрешности могут быть уменьшены:
1. Введение поправок
2. Градуированность графиков
3. Применение специальных методов, ┌например, метода замещения и других…┘
Пример:
Из-за случайных погрешностей, результаты измерения могут
быть как больше, так и меньше истинного значения.
Случайная погрешность записывается видом законов
распределения:
•
Интегральный
• Дифференциальный (чаще всего используется в измерительной технике)
Обозначения: P(X) – плотность распределения вероятности
Пример 1: Пусть измеряемая величина – X
77
Пусть, хотим знать будет ли результат «сидеть» в интервале (𝑋𝑋1 ; 𝑋𝑋2 )
𝑋𝑋2
𝑃𝑃{𝑋𝑋1 < 𝑋𝑋 < 𝑋𝑋2 } = � 𝑃𝑃(𝑥𝑥) 𝑑𝑑𝑑𝑑
𝑋𝑋1
Пример 2:
Из этого графика чаще всего встречается погрешность вблизи 0.
Нормальный закон распределения.
𝛿𝛿2̇
𝑃𝑃�𝛿𝛿1̇ < 𝛿𝛿̇ < 𝛿𝛿2̇ � = � 𝑃𝑃�𝛿𝛿̇ � 𝑑𝑑𝛿𝛿̇
𝛿𝛿1̇
Если нам известен закон распределения, то мы знаем все.
На практике используют числовые параметры законов распределения или моменты.
Моменты:
• Математическое ожидание M(X)
• Дисперсия D(X)
┌Мат. ожидание
+∞
𝑀𝑀(𝑋𝑋) = � 𝑋𝑋 ∗ 𝑃𝑃(𝑋𝑋)𝑑𝑑𝑑𝑑 [размерность измеряемой величины X]
−∞
Оценка мат. ожидания – это среднее значение измеряемой величины X при достаточно
большом числе измерений n.
𝑋𝑋� → 𝑀𝑀(𝑋𝑋)
∑𝑛𝑛𝑖𝑖=1 𝑥𝑥𝑖𝑖
�
𝑋𝑋=
𝑛𝑛
где n – число измерений, xi – значение случайной величины.
В качестве характеристики отклонения среднего используется дисперсия:
78
+∞
+∞
−∞
−∞
𝐷𝐷(𝑋𝑋) = � 𝑋𝑋 2 ∗ 𝑃𝑃(𝑋𝑋) 𝑑𝑑𝑑𝑑 = � [𝑥𝑥𝑖𝑖 − 𝑀𝑀(𝑋𝑋)]2 ∗ 𝑃𝑃(𝑋𝑋) 𝑑𝑑𝑑𝑑 = 𝐷𝐷(𝛿𝛿) [размерность 𝑋𝑋 2 ]
Из-за своей размерности (невозможно сравнить дисперсию и мат. ожидание, так как у
одной размерность X2, а у другого – X) дисперсия на практике заменяется
среднеквадратическим отклонением:┘
𝜎𝜎(𝑋𝑋) = �𝐷𝐷(𝑋𝑋) [размерность измеряемой величины 𝑋𝑋]
Таким образом получаем СКО с размерностью измеряемой величины и мат. ожидание
с той же размерностью.
СКО – разброс.
∆=kσ
k-?
В измерительной технике пользуются понятием
доверительного интервала погрешности.
Доверительный интервал погрешности – это те значения погрешности, за которые
не выходит погрешность измеряемой величины с вероятность PД .
Доверительный интервал погрешности с доверительной погрешностью
РД.
Причём, 𝑘𝑘 = 𝑓𝑓�𝑃𝑃(𝑋𝑋), 𝑃𝑃Д �.
Вероятность РД попадания погрешности в свой доверительный интервал обычна
довольно высока и составляет: от 0,8 до 0,(9).
Коэффициент k зависит от выбора закона распределения величины и доверительной
вероятности попадания погрешности в интервал.
79
Есть устройство
30. Идея суммирования погрешности
Варианты развития событий:
1. Известно все (каждая отдельно взятая ∆i, δi, γi) и необходимо найти суммарную
погрешность (тоже каждой отдельно взятой). Решается однозначно
теоретическая задача.
2. Известна суммарная погрешность (каждого) и необходимо найти погрешность
каждого из блоков. Эта задача является реальной, такой, которая решается в
современной технике. Однозначного решения этой проблемы нет.
Для решения задачи суммирования погрешностей вероятностным подходом,
необходимо знать не только ∆i, δi, γi, но и закон распределения ∆i, δi, γi. Тогда, строится
график закона распределения P(∆Σ, δΣ, γΣ).
К сожалению, если законы распределения разные, то построить суммарный закон
распределения очень сложно, чем более элементов.
Рассмотрим случай под номером один: тот, когда известны погрешности каждого
блока устройства и необходимо найти суммарную погрешность.
И при одинковых законах распределения, суммарный закон распределения может
иметь другой вид, даже при двух равномерных.
Рекомендации:
В случае, если мы не знаем закон распределения, но хотим включить РД , тогда можем
воспользоваться особенностью:
𝑃𝑃Д = 0,9 & 𝑘𝑘 = 1,8
𝑃𝑃Д = 0,95 & 𝑘𝑘 = 1,6
при которых можно даже не задумываться о законе распределения – все они (законы)
пересекаются в этих точках и, следовательно, любая гипотеза будет верна.
∆Σ=kσΣ, k=F(вид суммы закона распределения, PΣ ,РД).
Однако, на практике при суммировании погрешностей пользуются только 𝜎𝜎𝛴𝛴 .
Выясняется, что 𝜎𝜎𝛴𝛴 от закона распределения не зависит и для двух элементов:
𝜎𝜎𝛴𝛴 = �𝜎𝜎1 2 + 2𝑟𝑟𝜎𝜎1 𝜎𝜎2 + 𝜎𝜎2 2
r – коэффициент корреляции (коэффициент связи) между σ1 и σ2.
r>0 – что то растет и другое тоже растет (или оба убывают)
r<0 – что то растет, другое убывает.
0 ≤ |𝑟𝑟| ≤ 1
Принимаем r=0 или r=1 (на предприятиях)
r=0 – не связан (не коррелирован)
r=1 – жестко коррелирован (связан)
1. r=0
𝜎𝜎𝛴𝛴 = �𝜎𝜎1 2 + 𝜎𝜎2 2 – геометрическая сумма
80
2. r=±1
𝜎𝜎𝛴𝛴 = 𝜎𝜎1 ±𝜎𝜎2 – арифметическая сумма
Это, конечно, хорошо, но главный вопрос: как понять, коэффициент корреляции равен
нулю или равен единице.
Пример:
Предварительный и окончательный усилители, подключённые к источнику питания.
В этом случае коэффициент корреляции τ будет
равен единице, ибо у нас есть общая причина
нестабильности системы и это источник питания
ИП.
31. Получение результата измерений при обработке ряда прямых наблюдений
При многократных измерениях одной и той же измеряемой величины.
Идея: Пусть n – число измерений случайной величины X
Методы обработки различны, в зависимости от числа измерений n.
Ряд наблюдений – это последовательность значений случайной величины: X1, X2, X3,
… , Xn.
Методика обработки результатов наблюдений для n > 40
1. Необходимо выявить промахи (грубые ошибки в результатах, которые явно
выбиваются из общего ряда). Для этого есть специальные методики. Эти цифры
изымаются.
2. Ряд распределения, получаем в ходе эксперимента X1, X2, X3, … , Xn.
3. Осуществляется ранжирование значений. XMIN – на первое место; XMAX – на
последнее место.
4. Ищем 𝑋𝑋� среднее значение случайной величины X (или, осуществляем оценку
математического ожидания)
�
Х → при n→∞ →𝑀𝑀(𝑋𝑋)
∑𝑛𝑛𝑖𝑖=1 𝑥𝑥𝑖𝑖
𝑋𝑋� =
𝑛𝑛
5. Оцениваем СКО (среднеквадратичное отклонение)
𝑆𝑆̅ → при n→∞ →𝜎𝜎(𝑋𝑋)
∑𝑛𝑛𝑖𝑖=1(𝑋𝑋𝑖𝑖 − 𝑋𝑋�)
𝑆𝑆̅ = �
𝑛𝑛 − 1
6. Построение гистограммы (это функция, приближающая плотность
вероятности некоторого распределения, построенная на основе выборки из него)
∗
𝑃𝑃𝑛𝑛→∞
→ 𝑃𝑃(𝑋𝑋)
Интервал для деления оси абсцисс на графике-гистограмме выбирается по следующей
формуле
𝑋𝑋𝑀𝑀𝑀𝑀𝑀𝑀 − 𝑋𝑋𝑀𝑀𝑀𝑀𝑀𝑀
∆𝑋𝑋 =
5 (или 7)
(ОБЯЗАТЕЛЬНО делить на НЕЧЕТНОЕ число, иначе можно пропустить вершину).
81
mi – частота попадания случайной величины в интервал.
𝑚𝑚
𝑃𝑃 ∗ =
𝑛𝑛 ∗ ∆𝑋𝑋
По виду гистограммы с помощью критериев согласия (параметрических и
непараметрических) выдвигают гипотезу по поводу закона распределения и
проверяют её.
Чаще всего используют критерий χ2 «хи-квадрат» или критерий Пирсона.
Примечание:
Для облегчения подбора закона распределения существует реестр наиболее
распространенных законов:
7. Пишем результат измерения
̅
𝑆𝑆∗𝑘𝑘
𝑋𝑋 = А = 𝑋𝑋� ± 𝑛𝑛
√
𝑘𝑘 = 𝐹𝐹�𝑃𝑃(𝑋𝑋); 𝑃𝑃Д �
Оценка среднего
При определённых n = … и РД = …
Коэффициент k зависит от вида закона распределения и доверительной погрешности.
Примечание:
Существуют случаи, когда можно не строить закон распределения и гистограмму. Это
можно тогда, когда:
82
а) когда случай уже точно известен и обоснован в литературе, например
б) существуют случаи, когда можно с уверенностью утверждать, что закон
распределения – Гауссов
Рассмотрим случай, когда это можно утверждать. Из центральной предельной
теоремы теории вероятностей известно, что величина будет распределяться по
нормальному закону если на неё воздействует большое число независимых величин
(пять штук – уже достаточно), причём воздействие каждого из них незначительно.
Пусть X – величина. И мы считаем что она распределена по Гауссу.
Пример: Если закон распределения нормальный, только в этом случае имеем право
при n <= 10 (при малом числе измерений) пользоваться коэффициентом Стьюдента
𝑆𝑆̅ ∗ 𝜏𝜏�𝑛𝑛; 𝑃𝑃Д �
𝑋𝑋 = А = 𝑋𝑋� ±
√𝑛𝑛
При определённых n = … и РД = …
Коэффициент Стьюдента: 𝜏𝜏�𝑛𝑛; 𝑃𝑃Д �
32. Общие сведения об электромеханических приборах. Структурная схема.
Моменты, действующие в приборе. Классификация измерительных механизмов
и приборов на их основе кратко
Электромеханические приборы – относительно простые, относительно точны и не
требуют для своей работы внешнего источника питания. Это приборы, у которых под
действием измеряемой величины возникает механическая энергия поворота:
𝑥𝑥 ? → 𝑊𝑊мех → 𝛼𝛼 → 𝑥𝑥п − показания прибора
𝑥𝑥 ≡ 𝑊𝑊эл
ИЦ – измерительная цепь (чаще всего шунты и т.д.), служит для преобразования
входной электрической величины в другую электрическую величину.
ИМ – измерительный механизм, в нем происходит преобразование электрической
энергии в механическую.
ОУ – отсчетное устройство предназначено для визуального отображения результата:
𝛼𝛼 − угол поворота. Чаще всего α=90◌,
֯ иногда
α=135◌,
֯ очень редко α=3◌֯
(высокочувствительный прибор)
𝑋𝑋п = 𝑓𝑓(𝑋𝑋) ← функцияя преобразования –
однозначная связь (каждому значению Х
соответствует своё показание)
𝑋𝑋п = 𝐹𝐹( �
𝑃𝑃иц
, 𝑃𝑃�
𝑃𝑃оу , 𝑋𝑋)
им
��
�,
а)𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐
б)вводятся схемы
температурной
(частотной и т.д.)
компенсации
𝛼𝛼 = 𝐹𝐹(𝑋𝑋) − характеристика шкалы
𝑋𝑋п = 𝐹𝐹 ∗ (𝛼𝛼) – градуировочная характеристика
┌Пояснение для дальнейшего:
Электромеханический прибор состоит из трех частей: измерительная цепь,
измерительный механизм, отсчетное устройство.
83
Измерительная цепь служит для преобразования измеряемой электрической
величины в другу электрическую величину, непосредственно воздействующую на
измерительный механизм. В измерительном механизме электрическая энергия
преобразуется механическую энергию, что приводит к перемещению (повороту)
подвижной части. Отсчетное устройство служит для визуального отсчитывания
значений измеряемой величины в зависимости от угла поворота подвижной части.
Так как в измерительном механизме обычно имеет место угловое перемещение
подвижной части, то при анализе их работы рассматриваются моменты,
действующие на подвижную часть. Моменты подразделяются на статические и
динамические. Статическими являются моменты, действующие в механизме
всегда при наличии измеряемой величины. Динамические моменты действуют
на подвижную часть только при во время ее движения.
К статическим относятся вращающий и противодействующий моменты.
Момент, возникающий в механизме под действием измеряемой величины и
поворачивающий подвижную часть в сторону возрастающих показаний, называют
вращающим. Этот момент должен однозначно определяться измеряемой величиной
x и может зависеть от угла поворота подвижной части α, т.е вращающий момент
Mвр=F(x.α).
При повороте подвижной части на угол dα изменение механической энергии dA
равно изменению электрокинетической энергии dWэ в измерительном механизме,
т.е. dA = dWэ. При угловом перемещении подвижной части изменение
механической энергии dA = Mврdα, следовательно:
𝑑𝑑𝑊𝑊
𝑀𝑀вр = э ,
𝑑𝑑𝑑𝑑
где Wэ – электрокинетическая энергия измерительного механизма.
Таким образом, вращающий момент возникает, если электрокинетическая энергия в
механизме изменяется. В зависимости от типа механизма это может быть
изменение энергии электромагнитного поля (в большинстве приборов) или
электростатического поля (в электростатических приборах).
Чтобы подвижная часть не доходила всегда до упора при любом значении
измеряемой величины x, а поворачивалась на угол, зависящий от измеряемой
величины, на подвижную часть должен действовать момент, направленный
навстречу вращающему и зависящий от угла поворота подвижной части, противодействующий момент:
Mпр=F(α).
При некотором угле поворота наступает равенство Mвр=- Mпр.
Находят примерно шесть типов измерительных механизмов, отличающихся
способом создания вращающего момента, а именно: магнитоэлектрический,
электромагнитный, электродинамический, ферродинамический,
электростатический и индукционный.
По способу создания противодействующего момента измерительные механизмы
бывают с механическим противодействующим моментом и электрическим
противодействующим моментом – логометрические измерительные механизмы.
В измерительных механизмах с механическим противодействующим моментом
противодействующий момент создаётся упругими элементами (спиральными
пружинами, растяжками или подвесом), которые при повороте подвижной части
закручиваются.
При этом:
84
Mпр=-wα,
где w – удельный противодействующий момент, зависящий от свойств упругого
элемента. Упругие элементы используются в ряде приборов также в качестве
токоподводов к подвижной части.
В логометрических механизмах противодействующий момент создается также, как
и вращающий, но один из моментов должен зависеть от угла поворота подвижной
части. Если момент, создаваемый величиной x1, - вращающий, а момент
создаваемый величиной x2, - противодействующий, то
Mвр=F1(x1), Mпр=F2(x2, α), а α=Ф(x1/x2),
т.е. в этом случае угол поворота подвижной части определяется отношением
электрических величин x1 и x2.
При перемещении подвижной части на нее кроме указанных моментов действуют
также динамические моменты: момент сил инерции и момент успокоения.
Момент сил инерции MJ равен произведению момента инерции J на угловое
ускорение:
𝑑𝑑 2 𝛼𝛼
𝑀𝑀𝐽𝐽 = −𝐽𝐽 2 .
𝑑𝑑𝑡𝑡
Момент успокоения Mусп определяется как произведение коэффициента успокоения
P на угловую скорость:
𝑑𝑑𝑑𝑑
𝑀𝑀усп = −𝑃𝑃 .
𝑑𝑑𝑑𝑑
Знак «минус» в выражениях для моментов сил инерции и успокоения означают, что
эти моменты направлены навстречу вращающему.
Из теоретической механики известно, что при движении тела, вращающегося
(поворачивающегося) вокруг своей оси, момент сил инерции равен сумме
моментов, действующих на тело относительно оси вращения:
MJ= Mвр+ Mусп+ Mпр
Дифференциальное уравнение подвижной части:
𝑑𝑑𝑑𝑑
𝑑𝑑 2 𝛼𝛼
+ 𝑤𝑤𝑤𝑤 = 𝑀𝑀вр
𝐽𝐽 2 + 𝑃𝑃
𝑑𝑑𝑑𝑑
𝑑𝑑𝑡𝑡
┘
1) Момент вращения Мвр →
𝑑𝑑𝑊𝑊
Мвр = Э обязательное условие: Мвр=F(X), иногда может быть: Мвр=F(X, α)
𝑑𝑑𝑑𝑑
2) Противодействующий момент Мпр ← Мпр=F(α)!!!
Когда Мвр=Мпр - режим устойчивого равновесия
Пример
1.
85
2.
3.
Прибор вернется в первоначальное положение из-за возникновения устанавливающего
момента �𝑀𝑀уст � = 𝑀𝑀вр − 𝑀𝑀пр
4.
Существуют специальные конструкции, в которых возникает момент трения (из-за
конструкции).
𝑀𝑀тр − случайная величина, можно учесть, но не уменьшить
Крепления (из-за чего возникает Mтр)
86
3) Момент успокоения Мусп
Пример
𝛽𝛽 – степень успокоения (зависит
от конструкции прибора и от R, на
которое замкнута рамка)
1.Колебательный режим β<1
2.Апериодический режим β>1
3.Критический режим β=1 (дает
минимальное время успокоения)
В измерительных приборах
существует зона (±1% от длины
шкалы) - зона установившегося режима
𝑑𝑑𝑑𝑑
Муст = р ,
𝑑𝑑𝑑𝑑
р − коэффициент успокоения
Классификация:
1. По виду измеряемой величины
Амперметры, вольметры, омметры, частотометры, фазометры…
2. По роду электрического сигнала
Постоянного (=) или переменного (~) тока.
3. По способу создания противодействующего момента Mпр (было описано выше в
рамке)
Механические.
Логометры.
4. По способу успокоения
Воздушные.
Жидкостные.
Магнитоиндукционные.
5. По типу измерительного механизма (было описано в 5 вопросе)
Магнитоэлектронные.
Электромагнитные.
Электродинамические.
Электростатические.
Индукционные.
Ферродинамические.
87
33. Магнитоэлектрические приборы. Принцип действия м/э измерительного
механизма с механическим противодействующим моментом
Обозначение
С - Сердечник в виде эллипса
(неподвижный)
NS – постоянные магниты –
источник ЭДС (твердый
материал)
ПН – полюсные наконечники
сферической формы (мягкий
материал)
ПР – подвижная катушка (или
рамка с током)
Витки рамки с током оказываются
в поле с индукцией B. Это поле
радиальное и равномерное.
┌Пояснение для дальнейшего:
Ток к подвижной катушке (на рис.) подводится через две спиральные пружины (на
рис. они, где сердечник), основным назначением которых является создание
противодействующего момента. Вторая пружина на данном рисунке находится за
площадью чертежа (причина очевидна: рисунок двухмерный, а прибор – трёхмерный).
Внутренний конец пружины крепится на оси, проходящей через центр сердечника (на
рисунке – горизонтальная линия, разделяющая рисунок на две половины), а внешний –
на неподвижной части механизма.
Постоянный магнит (на рис.), являющийся источником магнитного поля, полюсные
наконечники (на рис.) и сердечник (на рис.), проводящие магнитный поток, образуют
так называемую магнитную систему прибора. Цилиндрическая форма сердечника и
расточки полюсных наконечников, а также их концентрическое расположение
обеспечивают равномерное радиальное поле в зазоре, т.е. в любой точке рабочего
зазора индукция магнитного поля B – величина постоянная. Воздушный зазор имеет
радиальную длину от одного до двух миллиметров.
В воздушном зазоре располагается подвижная катушка прямоугольной формы. Она
свободно охватывает сердечник и крепится на нём. Обмотка катушки – это медный
или алюминиевый провод.
Энергия механизма в данном случае состоит из трёх составляющих, а именно из
энергии магнита, энергии катушки и энергии взаимодействия магнита и катушки. В
создании вращающего момента участвует только третья составляющая, так как первые
две не зависят от угла поворота катушки (а, следовательно, и стрелки) α, а третья
составляющая зависит от него. Например, при горизонтальном расположении катушки
поле ПМов не проникает в катушку, а при её вертикальном расположении поле ПМов
полностью пронизывает катушку.
При наличии тока i в подвижной катушке энергия электромагнитного поля,
сцепляющегося с катушкой, т.е. энергия взаимодействия, определяется выражением
𝑊𝑊Э = 𝛹𝛹 ∗ 𝑖𝑖
88
где Ψ – потокосцепление подвижной катушки, Ψ = B*s*w*α ; B – индукция
магнитного поля в воздушном зазоре; s – площадь катушки; w – число витков обмотки
катушки; α – угол поворота.
Мгновенный вращающий момент определяется выражением
𝑑𝑑𝑊𝑊Э
= 𝐵𝐵 ∗ 𝑠𝑠 ∗ 𝑤𝑤 ∗ 𝑖𝑖
𝑀𝑀𝑡𝑡 =
𝑑𝑑𝑑𝑑
Если говорить, что ток синусоидальный (i=Im*sin(𝝎𝝎*t)), то вращающий момент 𝑀𝑀𝑡𝑡 =
𝐵𝐵 ∗ 𝑠𝑠 ∗ 𝑤𝑤 ∗ 𝐼𝐼𝑚𝑚 ∗ sin(𝜔𝜔 ∗ 𝑡𝑡) . При этом в соответствии с формулой для АЧХ подвижной
части электромеханического прибора (коим и является исследуемый):
1
𝐾𝐾(𝑗𝑗𝑗𝑗) =
�(1 − 𝑞𝑞 2 )2 + 4 ∗ 𝛽𝛽 2 ∗ 𝑞𝑞 2
𝜔𝜔
причём 𝑞𝑞 = - отношение колебаний
𝜔𝜔0
работа механизма зависит от соотношений частоты тока 𝝎𝝎 и частоты собственных
колебаний подвижной части механизма 𝝎𝝎0. У подобных механизмом период
собственных колебаний составляет примерно одну секунду (𝝎𝝎0 = 6, 28 с-1).
Следовательно, отклонение подвижной части измерительного механизма при частоте
тока более 10 Гц практически равно нулю. В диапазоне частот до 10 герц подвижная
часть колеблется с частотой входного тока, причём амплитуда колебаний зависит от
частоты. Поэтому приборы с такими измерительными механизмами применяются в
цепях постоянного тока. При протекании через катушку постоянного тока I
мгновенный вращающий момент
M = 𝐵𝐵 ∗ 𝑠𝑠 ∗ 𝑤𝑤 ∗ 𝐼𝐼
Если есть момент вращения, то должен быть и момент противодействия. И вот когда
они компенсируют друг друга – система находится в равновесии и можно снимать
какие-то ни было показания. Противодействующий момент
𝑀𝑀прот. = 𝑊𝑊 ∗ 𝛼𝛼
где W – удельный противодействующий момент, зависящий от свойств упругого
элемента.
Уравновесим систему: момент вращения равен моменту противодействия:
𝐵𝐵 ∗ 𝑠𝑠 ∗ 𝑤𝑤 ∗ 𝐼𝐼 = 𝑊𝑊 ∗ 𝛼𝛼
Откуда легко можно вывести
𝐵𝐵 ∗ 𝑠𝑠 ∗ 𝑤𝑤
∗ 𝐼𝐼
𝛼𝛼 =
𝑊𝑊
Чувствительность
где α – угол поворота стрелки, выходная величина; I – ток в рамке, входная величина;
SI – чувствительность
𝐵𝐵 ∗ 𝑠𝑠 ∗ 𝑤𝑤
= 𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐
𝑆𝑆𝐼𝐼 =
𝑊𝑊
Из предпоследнего выражения следует, что при постоянной индукции B в зазоре угол
отклонения подвижной катушки пропорционален току в катушке, а знак угла
отклонения меняется при изменении направления тока.
Прибор, из-за постоянства чувствительности,
имеет равномерную шкалу:
Итак, подытожим: был изучен
высокочувствительный, измеряющий токи от
10-16 ампер до единиц ампер, измерительный
89
прибор, который является полярным, то есть необходимо строго соблюдать
полярность: «плюс» и «минус» и работающий только на постоянном токе.
𝑑𝑑𝑊𝑊𝑒𝑒
┘
Мвр =
= 𝐵𝐵 ∗ 𝑆𝑆 ∗ 𝜔𝜔 ∗ 𝐼𝐼𝑝𝑝
Мпр = 𝑤𝑤 ∗ 𝛼𝛼
𝑑𝑑𝑑𝑑
S – площадь сечения рамки
𝜔𝜔 – число витков в рамке
𝑤𝑤 – удельный противодействующий момент и зависит от свойств пружины.
В момент равновесия:
Мвр=Мпр => 𝐵𝐵 ∗ 𝑆𝑆 ∗ 𝜔𝜔 ∗ 𝐼𝐼𝑝𝑝 = 𝑤𝑤 ∗ 𝛼𝛼
𝛼𝛼 =
𝐵𝐵∗𝑆𝑆∗𝜔𝜔
𝑤𝑤
���
чувствительность
∗ 𝐼𝐼𝑝𝑝
чувствительность 𝑆𝑆𝐼𝐼 = 𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐
Выводы:
1) шкала прибора равномерная и линейная
2) прибор обладает высокой чувствительностью
3) мкА, мА, мВ, мОм, 10-16 А гальванометр, ΔФ
4) достаточно точные приборы (кл.т. м/б 0,1!!! ; 0,2; 0,5; 1,5)
5) у них сильное внутреннее поле, поэтому отсутствует погрешность от магнитного
поля
6) имеют температурную погрешность
Недостатки:
1) измеряют только постоянные токи или переменные инфра низкой частоты (доли
Гц – Гц)
2) Из электромеханических они сейчас наиболее дорогие
34. Магнитоэлектрические приборы. Принцип действия м/э измерительного
механизма с электрическим противодействующим моментом
В магнитоэлектрических логометрических измерительных механизмах подвижная
часть выполняется в виде двух жёстко скреплённых между собой рамок, по обмоткам
которых текут токи I1 и I2. Ток к рамкам подводится с помощью металлических лент,
практически не имеющих противодействующего момента. Моменты МВРАЩ и МПРОТ,
создаваемые взаимодействием магнитного поля постоянного магнита и токов катушек,
90
направлены навстречу друг другу. Так как хотя бы один из моментов должен зависеть
от угла поворота подвижной части, то для этого, например, зазор выполняют
неравномерным, то есть
𝐵𝐵1 (𝛼𝛼) ≠ 𝐵𝐵2 (𝛼𝛼)
Моменты вращения и противодействия равны:
𝑀𝑀ВРАЩ = 𝑊𝑊1 ∙ 𝑆𝑆1 ∙ 𝐵𝐵1 (𝛼𝛼) ∙ 𝐼𝐼Р 1
𝑀𝑀ПРОТ = 𝑊𝑊2 ∙ 𝑆𝑆2 ∙ 𝐵𝐵2 (𝛼𝛼) ∙ 𝐼𝐼Р 2
где Wi – числа витков в катушках (рамках); Si – площади обхода катушек; Bi(α) –
соответствующая индукция; IP i – ток соответствующей рамки.
Условие равновесия системы не изменилось:
𝑀𝑀ВРАЩ = 𝑀𝑀ПРОТ
𝑊𝑊1 ∙ 𝑆𝑆1 ∙ 𝐵𝐵1 (𝛼𝛼) ∙ 𝐼𝐼Р 1 = 𝑊𝑊2 ∙ 𝑆𝑆2 ∙ 𝐵𝐵2 (𝛼𝛼) ∙ 𝐼𝐼Р 2
При условии, что число витков W1 = W2 = W и катушечные площади (длины рамок) S1
= S2 = S одинаковы, то:
𝐵𝐵1 (𝛼𝛼) ∙ 𝐼𝐼Р 1 = 𝐵𝐵2 (𝛼𝛼) ∙ 𝐼𝐼Р 2
Таким образом угол поворота стрелки α является функцией от отношения токов в
рамках. Всё верно, ведь логометр – прибор для измерения отношений.
𝐼𝐼
𝛼𝛼 = 𝑓𝑓 � Р 1�𝐼𝐼 �
Р2
┌Магнитоэлектрические измерительные механизмы имеют некоторые особенности,
которые придают магнитоэлектрическим приборам определённые положительные
свойства. Магнитоэлектрические измерительные механизмы имеют высокую
чувствительность и малое собственное потребление энергии, имеют линейную и
стабильную номинальную статическую характеристику преобразования
𝛼𝛼 = 𝑓𝑓(𝐼𝐼),
что объясняется стабильностью свойств применяемых материалов. У этих механизмов
отсутствует влияние электрических полей и мало влияние магнитных полей из-за
достаточно сильного поля в воздушном зазоре (0,2 – 1,2 Тл). Однако эти механизмы
имеют малую перегрузочную способность по току, относительно сложны и дороги.
Недостаток их также в том, что обычные механизмы реагируют только на постоянный
ток.┘
35. Магнитоэлектрические амперметры
1.мкА, мА, А
𝐼𝐼𝑝𝑝 = 𝐼𝐼𝐻𝐻 = мкА
𝛼𝛼 = 𝑆𝑆𝐼𝐼 ∗ 𝐼𝐼𝑝𝑝 = 𝑆𝑆𝐼𝐼 ∗ 𝐼𝐼𝐻𝐻
Если ток больше мкА, то рамку можем сжечь.
Поэтому применяем шунт (см.ниже)
91
2.Однопредельный амперметр
𝛼𝛼 = 𝑆𝑆𝐼𝐼 ∗ 𝐼𝐼𝑝𝑝
надо: 𝛼𝛼 = 𝐼𝐼н
Возникает температурная погрешность
1) без температурной погрешности
Rдоб – термистор
2)
Rдоб – не зависит от температуры
Многопредельный м/э амперметр
92
┌Пояснения ко всем рис. выше в этом вопросе:
В магнитоэлектрических амперметрах измерительный механизм включается в цепь
измеряемого тока либо непосредственно, либо при помощи шунта. Непосредственное
включение применяется при измерении малых токов (до 30 мА), допустимых для
токоподводов (пружинок, растяжек) и обмотки подвижной катушки механизма, т.е.
непосредственное включение возможно для микро и миллиамперметров. При больших
токах применяют шунты.
Изменение окружающей температуры влияет на магнитоэлектрический прибор
следующим образом:
1. При повышении температуры удельный противодействующий момент
пружинок (или растяжек) уменьшается на 0,2 – 0,4 % на каждые 10 кельвинов;
магнитный поток постоянного магнита, а следовательно и индукция,
уменьшаются приблизительно на те же 0,2 % на каждые 10 кельвинов. Таким
образом эти два явления уравновешивают друг друга и получается, что в
приборах малой и средней точности температурные влияния пренебрежимо
малы.
2. Изменяется электрическое сопротивление обмотки катушки и токоподводов.
Это влияние – основной источник температурной погрешности
магнитоэлектрических приборов.
Амперметры без шунта не
имеют температурной
погрешности. В амперметрах с
шунтом температурная
погрешности может оказаться
значительной вследствие
перераспределения токов между
шунтом и подвижной катушкой.
Для её уменьшения применяют специальные цепи температурной компенсации, одна
из которых показана на рисунке выше. В этом случае температурная погрешность
снижается за счёт включения последовательно с подвижной катушкой резистора R из
манганина.
Зависимость угла поворота стрелки прибора от тока через рамку имеет следующий
вид:
𝛼𝛼 = 𝑆𝑆𝐼𝐼 ∙ 𝐼𝐼Р
93
где α – угол поворота стрелки, выходная величина; SI – чувствительность прибора;
IР – ток через рамку.
Ток через рамку должен быть мал, для недопущения больших погрешностей.
Шунтирующие сопротивления играют роль масштабных преобразователей.
В многопредельных амперметрах для изменения пределов измерения применяют
многопредельные шунты. Поэтому многопредельные амперметры снабжают
переключателями диапазонов измерений или снабжают несколькими входными
зажимами.┘
Магнитоэлектрический гальванометр
Измеряет очень маленькие токи (до 10-15)
𝑆𝑆𝐼𝐼 =
𝐵𝐵𝐵𝐵𝐵𝐵
𝑤𝑤
𝛼𝛼 = 𝑆𝑆𝐼𝐼 ∗ 𝐼𝐼𝑝𝑝 , 𝛼𝛼 ≅ 3°, 𝑆𝑆𝐼𝐼 должна быть большая
как увеличить? надо уменьшить 𝑤𝑤.
Мпр=w*α
d должно быть больше 1,4 м.
Световой отсчет
- не пишут класс точности!!!
Но существуют гальванометры, у которых пишут класс точности.
Уравнение движения подвижной части гальванометра:
𝑑𝑑 2 𝛼𝛼
𝐽𝐽 2
+
𝑑𝑑𝑡𝑡
Момент
Инерции
Где 𝛼𝛼 = 𝑆𝑆𝐼𝐼 ∗ 𝐼𝐼𝑝𝑝
𝑑𝑑𝑑𝑑
𝑝𝑝
𝑑𝑑𝑑𝑑
Момент
успокоения
+
𝑤𝑤𝑤𝑤
=
Момент
противодействия
94
𝐵𝐵𝐵𝐵𝐵𝐵𝐼𝐼𝑝𝑝
Момент
вращения
𝛽𝛽 – степень успокоения
𝛽𝛽 = 𝐹𝐹(𝑁𝑁, 𝑝𝑝, 𝐽𝐽)
𝛽𝛽 =
𝑝𝑝
√𝐽𝐽𝑤𝑤
Время установления показаний
Мусп зависит от параметров: β и сопротивление, на которое замкнута рамка (R*)
Гальванометры работают в
критическом режиме
Баллистический
гальванометр
Разновидность
магнитоэлектрического гальванометра с увеличенным моментом инерции: J=Jmax
𝐽𝐽𝑚𝑚𝑚𝑚𝑚𝑚 => 𝑇𝑇0 (период свободных колебаний; опреедляется конструкцией) тоже
большой =>
=>
В рамку гальванометра подается коротки импульс τ<0.1T0
Прибор, который увеличивает J, сначала накапливает энергию, а потом
поворачивается
𝛼𝛼𝑚𝑚𝑚𝑚𝑚𝑚 ≡ 𝑄𝑄‼!
Баллистический гальванометр измеряет количество электричества, можно также
измерять изменение постоянного магнитного потока ΔФ.
95
36. Магнитоэлектрические вольтметры
Rн || Rv , Rv большое.
А) Однопредельный вольтметр
Б)
𝛼𝛼 = 𝑆𝑆𝐼𝐼 ∗ 𝐼𝐼𝑝𝑝 ,
𝐼𝐼𝑝𝑝 =
Rдоб из манганина
𝑈𝑈
𝑈𝑈
=> 𝛼𝛼 = 𝑆𝑆𝐼𝐼 ∗
= 𝑓𝑓(𝑈𝑈)
𝑅𝑅𝑝𝑝 + 𝑅𝑅доб
𝑅𝑅𝑝𝑝 + 𝑅𝑅доб
┌В магнитоэлектрических
вольтметрах для получения нужного
диапазона измерений
последовательно с измерительным
механизмом включают добавочный
резистор стабильного
сопротивления, например
выполненный из манганина.
В многопредельных вольтметрах
используют несколько добавочных
резисторов (наш случай). Поэтому
многопредельные
вольтметры
снабжают переключателем диапазонов или несколькими входными зажимами.
Пропорциональная зависимость угла отклонения подвижной части от тока в катушке
приводит к равномерной шкале у магнитоэлектрических амперметров и вольтметров.
Добавочные сопротивления обычно составляют несколько кОм. Таким образом они
увеличивают внутреннее сопротивление
прибора.┘
Примечание: при переключении пределов
измерения, если не предпринять меры, то
на разных пределах будут разные
сопротивления. Делают
компенсированные переключатели.
96
37. Индукционные измерительные механизмы
Все катушки на магнитопроводах говорят о том, что есть вихревые токи. Для того,
чтобы индукционно-измерительный механизм работал, надо не менее 2-х переменных
магнитных потока, сдвинутых в пространстве и времени.
Токи i1 и i2, текущие по катушкам:
𝑖𝑖1 = 𝐼𝐼𝑚𝑚1 ∙ sin(𝜔𝜔 ∙ 𝑡𝑡)
𝑖𝑖2 = 𝐼𝐼𝑚𝑚2 ∙ sin((𝜔𝜔 ∙ 𝑡𝑡) − 𝜑𝜑)
Очень важно то, что эти два тока сдвинуты относительно друг друга по фазе, о чём
нам говорит φ у тока i2.
Имеем два магнитопровода с двумя обмотками. Поскольку токи, пущенные по
обмоткам - переменные, возникают два магнитных потока: Ф1t и Ф2t.
𝑖𝑖1 → Ф1𝑡𝑡 → 𝐸𝐸1 → 𝑖𝑖11
𝑖𝑖2 → Ф2𝑡𝑡 → 𝐸𝐸2 → 𝑖𝑖22
причём inn – соответствующий вихревой ток.
ПМ (постоянный магнит, магнитопровода) создаёт аналог противодействующего
момента(тормозящий момент).
Построим ВД:
97
Одной дугой обозначен угол φ, угол между
токами I1 и I2. Двумя дугами обозначены
углы δ, углы между соответствующими
токами и магнитными потоками. Ломаной
линией обозначены прямые углы между
соответствующими МДС и магнитными
потоками.
и вихревых токов.
Момент вращения создаётся за счёт
взаимного перемещения магнитных потоков
𝑀𝑀вр 𝑡𝑡 = Ф1 𝑡𝑡 ∙ 𝑖𝑖22 + Ф2 𝑡𝑡 ∙ 𝑖𝑖11
Из физики известно, что вихревые токи пропорциональны частоте:
i11 =c*f*Ф1t
i22=c*f*Ф2t
Mврt=cf(Ф1t+Ф2t)
Измерительный механизм обладает большим моментом инерции; реагирует не на
мгновенные, а на средние.
𝑇𝑇
Тогда
1
𝑀𝑀вр = � 𝑀𝑀вр 𝑡𝑡 𝑑𝑑𝑑𝑑
𝑇𝑇
0
𝑀𝑀вр = с ∙ Ф1 ∙ Ф2 ∙ sin�Ф�
1 , Ф2 �
Для создания момента вращения необходимо иметь не менее двух магнитных потоков,
сдвинутых друг относительно друга в пространстве и во времени.
38. Магнитоэлектрические омметры
М/э логометр (омметр)
┌
Прибор предназначен для
измерения сопротивления RX.
Интересно то, что в данном
примере сопротивление Rдоб,
включённое последовательно с
измеряемым RX, выполняет
роль ограничителя и, при
коротком замыкании
измеряемого RX, рамки,
благодаря этому самому Rдоб, не
выйдут из строя.
В данном случае сопротивление
изоляции, для обеспечения
безопасности, должно быть
большим, в этом случае токи
будет малыми, но для этого
необходимо большое
напряжение питания.┘
98
При
𝐼𝐼Р 1 =
𝑈𝑈ПИТ
𝑅𝑅𝑋𝑋 +𝑅𝑅доб
и
𝐼𝐼
𝐼𝐼
𝛼𝛼 = 𝑓𝑓 � Р 1�𝐼𝐼 � = 𝑓𝑓 � 1�𝐼𝐼 � =
𝐼𝐼Р 2 =
𝑈𝑈ПИТ
Р2
2
𝑅𝑅0
Получаем, что
𝑈𝑈
𝑈𝑈
𝑅𝑅
𝐼𝐼
𝛼𝛼 = 𝑓𝑓 � 1�𝐼𝐼 � = 𝑓𝑓 � ПИТ : ПИТ� = 𝑓𝑓 � 0 � = 𝑓𝑓(𝑅𝑅𝑋𝑋 ) ≠ 𝑓𝑓(𝑈𝑈)
𝑅𝑅𝑋𝑋 +𝑅𝑅доб 𝑅𝑅0
𝑅𝑅𝑋𝑋 +𝑅𝑅доб
2
На практике независимость напряжения по фазе сохраняется при ±20%. Если
напряжение меняется, то используем 𝛼𝛼 = 𝑓𝑓(𝑈𝑈)
На базе этих Логометров выпускают мегомметры (МГОм)
39. Индукционный счетчик энергии
Счетчик – интегральный прибор, измеряет мощность за время.
W=Pt
Энегрия измеряется в данном случае в кВт*ч.
1) индукционный механизм – измеряет мощность за время
2) счётный механизм (за время) – считывает обороты подвижного диска
Реально:
W=Cном*Nобр
Nобр - количествово оборотов
CHОМ – постоянная счётчика �кВт ∙ час�обороты�
Действительно:
W=Cдейст*N; Cдейст≠Сном(т.е. очень мало)
Принцип действия индукционных измерительных механизмов основан на
взаимодействии магнитных потоков и вихревых токов (как уже отмечалось ранее),
индуцированных магнитными потоками в подвижной части механизма, выполненной
в виде алюминиевого диска.
В настоящее время из индукционных приборов
находят применение счётчики электрической
энергии в цепях переменного тока.
M1 —ТО(т.е. обмотка тока),
M1 —ОН(т.е. обмотка напряжения).
99
Токовая обмотка на П-образном магнитопроводе включается последовательно с
нагрузкой. А обмотка напряжения включается параллельно напряжению (число витков
стремится к бесконечности) и поэтому на векторной диаграмме поток от ЭДС(E)
отстаёт почти на 90 градусов.┘
ПМ (постоянный магнит) создаёт аналог противодействующего момента (тормозящий
момент).
Мвр=Мтормоз
┌На подвижную часть счётчика действует
тормозной момент, пропорциональный скорости вращения диска. Этот момент
создаётся в результате действия тока, наводимого во вращающемся между полюсами
постоянного магнита диске, и определяется выражением:┘
𝑑𝑑𝑑𝑑
Мтор=k
𝑑𝑑𝑑𝑑
𝑑𝑑𝑑𝑑
− скорость вращения диска
𝑑𝑑𝑑𝑑
Начертим ВД:
┌Токовая обмотка (ТО) создаёт магнитный поток, который пропорционален току
нагрузки IH. А вот обмотка по напряжению (ОН) создаёт другой магнитный поток,
пропорциональный напряжению U.
ТО → Ф𝟏𝟏 ~ 𝑰𝑰𝑯𝑯
ОН → Ф𝟐𝟐 ~ 𝑼𝑼
А «тормозной момент» (читай: противодействующий или успокаивающий момент)
создаётся тормозящим магнитом, который направляет своё действие на алюминиевый
диск.┘
100
Мвр= Ф1Ф2sin(Ф1^ Ф2)
Ф1=kIн; Ф2=U/(wLон); sin(Ф1^ Ф2)=sin(β-φ-δ)
P=UIнcos φ -это надо
Имеем: Мвр=kUIнsin(β-φ-δ)
cos φ= sin(β-φ-δ)
Достигается β-δ=90°, тогда cos φ = sin(90°- φ)
𝑑𝑑𝑑𝑑
Проинтегрируем по
𝑑𝑑𝑑𝑑
Мвр и Мтор
𝑡𝑡
𝑡𝑡 𝑑𝑑𝑑𝑑
𝑘𝑘1 ∫0 P dt = 𝑘𝑘2 ∫0
dt
𝑑𝑑𝑑𝑑
Cном=k1/k2
W=CномN - энергия (интеграл от мощности),
прошедшая через счётчик за интервал времени
от 0 до T
┌Отсчёт производится по показаниям счётного
механизма – счётчика оборотов, градуированного в единицах энергии. Единице
электрической энергии (один киловатт-час), регистрируемой счётным механизмом,
соответствует определённое число оборотов подвижной части счётчика (диск из
алюминия). Это соотношение, называемое передаточным числом А, указывается на
счётчике.┘
40. Электродинамические измерительные механизмы
Наиболее точные приборы для измерения переменных токов, которые обладают
большим частотном диапазоном
Они являются идеальными множительными
приборами, на их базе изготавливают ваттметры.
P=UIcosφ
Работает на постоянном и переменном токе до 20кГЦ.
Недостаток:
• Не любят внешние магнитные поля, т.к. внутреннее магнитное поле маленькое,
чтобы этого не было для защиты ставят внутри прибора защитные экраны, за
счет чего увеличиваются габариты
• Не высокочувствительные: mA, A, mB, B, но не мк
Ферродинамические (все катушки на 20-50 Гц
сердечниках) обладают большим моментов вращения
(используется на кораблях).
Работает на постоянном и переменном токе порядка 50 Гц,
400 Гц.
Железо (магнитомягкое)
101
Электродинамический измерительный механизм
1
1
1
2
2
2
∗ 𝐿𝐿НК1 ∗ 𝐼𝐼НК1
+ ∗ 𝐿𝐿НК2 ∗ 𝐼𝐼НК2
+ ∗ 𝐿𝐿ПК ∗ 𝐼𝐼ПК
+ 𝑀𝑀 ∗ 𝐼𝐼НК ∗ 𝐼𝐼ПК
2
2
2
где M – коэффициент взаимной индуктивности двух катушек: подвижной и
неподвижной.
Вращающий момент:
𝑑𝑑𝑊𝑊Э
𝑀𝑀ВРАЩ =
𝑑𝑑𝑑𝑑
На постоянном токе:
𝑑𝑑𝑑𝑑
𝑀𝑀ВРАЩ = 𝐼𝐼НК ∙ 𝐼𝐼ПК ∙
𝑑𝑑𝑑𝑑
На переменном токе:
𝑑𝑑𝑑𝑑
𝑀𝑀ВРАЩ = 𝑖𝑖НК ∙ 𝑖𝑖ПК ∙
𝑑𝑑𝑑𝑑
Поскольку этот механизм обладает большим моментом инерции, то он не успевает
реагировать на мгновенное значение, а реагирует на среднее.
𝑊𝑊Э =
𝑇𝑇
1
𝑀𝑀ВРАЩ сред = ∗ � 𝑀𝑀ВРАЩ 𝑡𝑡 𝑑𝑑𝑑𝑑
𝑇𝑇
0
𝑑𝑑𝑑𝑑
𝑑𝑑𝑑𝑑
𝐼𝐼НК ∙ 𝐼𝐼ПК − действующие значения
�
𝑀𝑀ВРАЩ = 𝐼𝐼НК ∙ 𝐼𝐼ПК ∙ cos�𝐼𝐼НК
, 𝐼𝐼ПК �
┌Итак, подытожим:
• На переменном токе устройство измеряет действующее значение
• Для переменном токе шкала будет нелинейной
• Является самым высокоточным прибором переменного тока
• Прибор является идеальным перемножителем (те два тока: ток неподвижной и
подвижной катушки)
Недостатки:
• Невысокая чувствительность
• Требуется защита от внешних магнитных полей, поскольку его собственное
магнитное поле очень мало┘
102
a) mA,A
41. Электродинамические амперметры
Амперметры
Схема для измерения малых токов
б) Схема для измерения токов побольше
Iн=I1+I2
Rпк=Rнк+Rдоб
𝑑𝑑𝑑𝑑
~α=(1/W)*Iнк*Iпкcos(Iнк^Iпк)
𝑑𝑑𝑑𝑑
Rпк - большое сопротивление
Rнк – малое сопротивление
RДОБ добавляется для того, чтобы I1=I2
𝑑𝑑𝑑𝑑
Iнк*Iпк=Iн2 ;
α=(1/W)* (Iн)2* ; шкала
𝑑𝑑𝑑𝑑
неравномерна
┌ В электродинамических и ферродинамических амперметрах для токов до 0,5 А
неподвижные и подвижная катушки измерительного механизма соединяют
последовательно. В этом случае токи в катушках равны, т. е. I=
I=
I ; cosγ =1 и
1
2
угол отклонения
1 dM 1,2 2
⋅ I (5-21)
W dα
Для получения линейной зависимости α = f ( I ) , а следовательно равномерной
α =⋅
шкалы, у электродинамических амперметров так располагают неподвижные катушки,
чтобы зависимость
dM 1,2
dα
= ϕ (α ) корректировала функцию (5-21), приближая ее к
линейной. Практически у электродинамических амперметров шкала равномерна в
пределах 25—100 % ее длины.
При последовательном включении катушек температурная и частотная (до 2000
Гц) погрешности электродинамических амперметров незначительны.
В амперметрах на токи свыше 0,5 А подвижную и неподвижные катушки
включают параллельно. В этом случае осуществляют компенсацию температурной и
частотной погрешностей, возникающих из-за перераспределения токов в катушках
при изменении температуры и частоты. Компенсацию температурной погрешности
осуществляют подбором сопротивлений добавочных резисторов из манганина и меди,
включаемых в каждую из параллельных ветвей так, чтобы температурные
коэффициенты сопротивления этих ветвей были одинаковыми. Компенсацию
частотной погрешности выполняют включением добавочных катушек индуктивности
или конденсаторов в соответствующие ветви схемы так, чтобы были равными
постоянные времени этих ветвей.
103
Для схемы с параллельным включением катушек и при выполнении условий
температурной и частотной компенсации
=
I1 c=
c2 I ; cosγ =1, где I1 , I 2 —
1I ; I2
токи в неподвижных и подвижной катушках; I — измеряемый ток. Угол отклонения
подвижной части амперметра при этом
cc
W
α =1 2 ⋅
dM 1,2
dα
⋅I2
Электродинамические амперметры чаще всего выпускают на два диапазона
измерений. Изменение пределов при этом производится путем включения
неподвижных катушек последовательно или параллельно. Для расширения пределов
измерения используют измерительные трансформаторы тока.
┘
42. Электродинамические вольтметры
Rдоб>>1>Rнк+Rпк
1
α= ∗
𝑊𝑊
𝑈𝑈 2
(𝑅𝑅нк +𝑅𝑅пк +𝑅𝑅доб
)2
∗
𝑑𝑑М
𝑑𝑑𝑑𝑑
;
α=𝑈𝑈 2
Для вольтметра на переменном токе:
𝑍𝑍общ = �(𝑅𝑅нк + 𝑅𝑅пк )2 + (𝑤𝑤𝑤𝑤)2
L-индуктивность неподвижной катушки и подвижной катушки
возникает частотная погрешность: α=F(U,w)
Почти реальная схема
Добавочное сопротивление
делают из двух частей:
1
𝑧𝑧𝑐𝑐 =
𝑗𝑗𝑗𝑗𝑗𝑗
𝑍𝑍𝑅𝑅доб1+𝑅𝑅доб2+𝑍𝑍𝑍𝑍 = 𝜔𝜔𝜔𝜔
При увеличении частоты идёт
падение на резисторах,
компенсируем это введением шунтирующего сопротивления, эквивалентного
сопротивлению катушек.
При ω=var
𝑍𝑍всего = 𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐
┌ Электродинамический вольтметр состоит из электродинамического
измерительного механизма и добавочного резистора стабильного сопротивления,
причем все катушки механизма и добавочный резистор включены последовательно.
Угол отклонения подвижной части электродинамического вольтметра
c dM 1,2 2
⋅U
W dα
α =3 ⋅
2
где c3 = 1 / Z ; Z — полное сопротивление цепи вольтметра, т. е. сумма
сопротивлений катушек и добавочного резистора.
В многопредельных вольтметрах последовательно с измерительным механизмом
включается секционированный добавочный резистор. Поэтому многопредельные
вольтметры снабжают переключателем пределов или несколькими входными
зажимами. Для увеличения верхнего предела измерений вольтметра применяют
измерительные трансформаторы напряжения.
104
В электродинамических вольтметрах при изменении температуры возникает
температурная погрешность от изменения сопротивления цепи вольтметра. В
вольтметрах с малым верхним пределом измерений температурная погрешность
может достичь недопустимой величины. Поэтому в таких вольтметрах уменьшают
сопротивление катушек, уменьшая число витков, что приводит к увеличению тока,
потребляемого прибором. Частотная погрешность, вызванная изменением Z прибора,
компенсируется путем шунтирования части добавочного резистора конденсатором.┘
43. Электродинамические ваттметры
Мощность
𝑃𝑃 = 𝑈𝑈 ∙ 𝐼𝐼Н ∙ cos(𝜑𝜑)
Исходная схема и векторная диаграмма будут выглядеть так:
Схема включения ваттметра:
В этом случае последовательно соединённые неподвижные катушки НК1 и НК2
включают последовательно с объектом нагрузки ZН, потребляемая мощность
которого измеряется. Подвижная катушка ПК с добавочным резистором RДОБ
включается параллельно объекту измеряемой мощности. Цепь неподвижных
катушек называют последовательной цепью, а цепь подвижной катушки –
параллельной цепью.
Ток подвижной катушки:
𝑈𝑈
𝐼𝐼ПК =
2
�(𝜔𝜔 ∙ 𝐿𝐿ПК )2 + �𝑅𝑅ПК + 𝑅𝑅ДОБ �
Векторная диаграмма: (γ – из-за индуктивности)
105
Угол 𝛄𝛄 очень мал, так как добавочное сопротивление 𝑅𝑅ДОБ велико. Также, из
расчётов предыдущего устройства, известно, что:
�
𝛼𝛼 = 𝑘𝑘 ∙ 𝐼𝐼НК ∙ 𝐼𝐼ПК ∙ cos�𝐼𝐼НК
, 𝐼𝐼ПК �
1 𝑑𝑑𝑑𝑑
𝑘𝑘 =
𝑊𝑊 𝑑𝑑𝑑𝑑
�
cos�𝐼𝐼НК
, 𝐼𝐼ПК � = cos(𝜑𝜑 − 𝛾𝛾)
Для ваттметра получаем выражение поворота стрелки:
𝑈𝑈 ∙ cos(𝛾𝛾)
𝑑𝑑𝑑𝑑
1
∙ cos(𝜑𝜑 − 𝛾𝛾) ∙
𝛼𝛼 = ∙ 𝐼𝐼𝐻𝐻 ∙
𝑑𝑑𝑑𝑑
(𝑅𝑅ПК + 𝑅𝑅ДОБ )
𝑊𝑊
Формула мощности имеет вид:
𝑃𝑃 = 𝑈𝑈 ∙ 𝐼𝐼Н ∙ cos(𝜑𝜑)
Поэтому, хотим чтобы:
𝛼𝛼 ≡ 𝑃𝑃
То есть угол поворота стрелки прибора отражал бы измеряемую мощность.
Это возможно в следующем случае:
Если 𝛾𝛾 → 0, то cos(𝛾𝛾) → 1 и тогда cos(𝜑𝜑 − 𝛾𝛾) → cos(𝜑𝜑)
И в этом случае угол поворота будет определяться:
𝛼𝛼 = 𝑘𝑘 ∙ 𝑃𝑃
𝑑𝑑𝑑𝑑 1
𝐼𝐼𝐻𝐻
где P = U ∙ I – измеряемая мощность; коэффициент k =
∙ ∙
𝑑𝑑𝑑𝑑
𝑊𝑊 (𝑅𝑅ПК +𝑅𝑅ДОБ )
чувствительность прибора. У ваттметров конструктивными методами добиваются
𝑑𝑑𝑑𝑑
= 𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐, что обеспечивает равномерную шкалу.
𝑑𝑑𝑑𝑑
44. Общие сведения об электронных приборах
┌ Из онлайн-лекций:
Электронные аналоговые измерительные приборы и преобразователи представляют
собой такие средства измерений, в которых преобразование сигналов
измерительной информации осуществляется с помощью аналоговых электронных
устройств. Выходной сигнал в электронных аналоговых средствах измерений
является непрерывной функцией измеряемой величины. Применение электронных
устройств в средствах измерений обусловлено, в первую очередь, возможностью
повышения ряда важных метрологических и других функциональных
характеристик таких средств измерений. Наиболее важными метрологическими
характеристиками электронных аналоговых измерительных приборов являются:
высокая чувствительность, широкий диапазон измерений, относительно малая
потребляемая мощность от измерительной цепи (или большое входное
сопротивление), широкий частотный диапазон измеряемых величин. Применение
аналоговой электронной техники может привести к увеличению погрешностей
преобразования сигналов. Поэтому во многих случаях аналоговые электронные
приборы имеют сравнительно невысокие классы точности. Широкие
функциональные возможности открываются при использовании в средствах
измерений электронно-лучевых трубок, позволяющих осуществить визуализацию
сигналов. В первую очередь эти возможности реализуются в электронно-лучевых
осциллографах. Электронные средства измерений принципиально могут быть
применены для измерений практически всех электрических и многих
неэлектрических величин. Эти уникальные возможности электронных средств
106
измерений нашли свое применение при создании измерительных преобразователей.
Такие преобразователи, в частности, используются в информационноизмерительных системах. Среди показывающих средств измерений – приборов в
настоящее время широкое признание получили такие электронные измерительные
приборы как электронно-лучевые осциллографы, электронные вольтметры,
омметры, анализаторы спектра и др. Эти приборы имеют ряд достоинств,
положительно отличающих их от других средств измерений. В то же время
некоторые аналоговые приборы, например, частотомеры и фазометры, вытесняются
соответствующими цифровыми приборами, что обусловлено относительной
простотой преобразования этих параметров в кодовый сигнал.
┘
Электронные приборы и преобразователи — СИ, в которых преобразование
сигнала измерительной информации осуществляется с помощью электронных
устройств. Выходной сигнал таких СИ является непрерывной функцией входного
сигнала.
Такие СИ используются, в частности, для измерения любых электрических
величин: тока, напряжения, сопротивления и т.п.
Достоинства
• Высокая чувствительность — достигается за счет электронных схем, как
правило, операционных усилителей.
• Широкий диапазон измеряемых значений.
• Малое потребление из измерительной цепи.
• Широкий частотный диапазон измерительных сигналов.
Среди электронных аналоговых измерительных преобразователей широкое
распространение получили преобразователи с унифицированным выходом
(выходным сигналом):
Действительно, поскольку число n измерительных преобразователей в
информационно-измерительной системе может быть весьма большим,
измерительные каналы удобно делать унифицированными — выдающими сигнал
одного вида.
Унифицированные сигналы:
• по напряжению: 0 ÷ 10 В;
• по току: 0 ÷ 5 мА.
Если такие унифицированные сигналы снимают с выхода датчиков, то все, что идет
далее по измерительному тракту, может быть совершенно одинаковым.
Следовательно, и обрабатывается одинаково. Это означает существенное
удешевление измерительной системы.
107
45. Электронный комбинированный вольтметр
Такие вольтметры предназначены для измерения напряжения постоянного и
переменного токов в широком диапазоне частот.
На схеме:
УПТ – это усилитель постоянного тока. К нему подсоединены два (условно)
подключённых к нему резистора, предназначенных, один – для установки нуля,
другой – для калибровки. П – переключатель с пятью возможными положениями. E0 образцовый стабильный источник питания; R0i – это образцовые сопротивления. В
универсальных вольтметрах, называемых также комбинированными, часто
присутствует возможность измерения сопротивления RX (на рисунке присутствует). В
зависимости от положения переключателя, прибор занимается либо установкой нуля и
калибровкой (подготовка к работе), либо непосредственно измерением переменного и
постоянного напряжения (основная функция), либо измерить неизвестное
сопротивление RX (дополнительная функция). Для измерения напряжения на
кабельный вход ( ) подаётся либо постоянное напряжение, либо переменное(на
разные, разумеется, кабельные входы). Буква Д в квадратике – это детектор,
предназначенный для преобразования переменного напряжения в постоянное. А
нужен он для того чтобы преобразовать переменный сигнал приходящий к нему на
вход в постоянный сигнал для усилителя постоянного тока.
108
Детекторы бывают:
• Выпрямительные (например, диод) или «среднего значения»
• Синхронные (с высокой помехоустойчивостью)
• Амплитудные
• Действующего значения
В предложенной схеме почти наверняка будет детектор действующего значения.
Работа схемы:
• Подготовка к работе:
1ОЕ положение переключателя – фактическое КЗ (короткое замыкание). Смотрим на
самую точную из шкал, проверяя, нуль ли показан на шкале; если не нуль – не
забываем, что у нас не простой резистор, а реостат и делаем сопротивление таким,
чтобы указатель (стрелка? заяц?) показывал нуль.
2ОЕ положение переключателя – измеряем падение напряжения на образцовом
резисторе R02. Если по самой точной шкале показывает нуль – всё замечательно.
Если что-то не так, опять-таки помним про свойства реостата. Можем приступить
непосредственно к измерению.
• Основное функции прибора:
3Е положение переключателя – измеряем поданное на кабельный вход постоянное
напряжение.
4ОЕ положение переключателя – измеряем конвертированное в постоянное,
переменное напряжение, поданное на кабельный вход.
• Дополнительные функции прибора:
5ОЕ положение переключателя: подключаем к клеммам неизвестно, но искомое
сопротивление RX и снимаем падение напряжения на RX (прям как во втором
положении). Падение напряжения будет пропорционально искомому
сопротивлению.
Обычно электронные приборы градуируют в действующих значения
синусоидального напряжения. Если на вход вольтметра подаётся напряжение,
отличное от синусоидального, то возникает погрешность от формы кривой,
которую необходимо учитывать (погрешность). К вышенаписанному – пример на
следующей странице…
Пример:
Пример 1
109
Umax=KA*U
Uвх=КА*Uп/ КА. КА*Uп в числителе из-за АД.
Если в электронном вольтметре стоит детектор действующего значения, то Uп=Uвх.
Uвх
А)
Б)
КА=1,41
КА=1
КА=…неизвестно
В)
46. Электронные вольтметры постоянного тока с преобразованием спектра
Может измерять мВ, В, мкВ!!!
М – модулятор – преобразует постоянный ток в переменный
Данный вид можно получить с помощью ключа.
Частота работы модулятор такая, с какой включается
ключ.
- усилитель переменного тока.
ДМ – демодулятор (выпрямитель) – преобразует
переменный ток в постоянный, т.к. м/э им работает на
постоянном токе
110
БП – блок питания, не всегда блок питания стоит один, бывает, что их ставят
несколько, причиной этому могут быть помехи.
Схема близкая к реальной!!!
Может измерять мВ, В, мкВ!!!
Ф – фильтр – обычно ставят на входе, но не всегда, т.к. о н может ухудшить
динамические процессы.
У3 – согласующий усилитель (для согласования усилительного режима с
нагрузкой).
┌Вольтметры постоянного тока редко используют как самостоятельные приборы, в
то же время их широко применяют в составе универсальных вольтметров. Для
создания высокочувствительных вольтметров постоянного тока
(микровольтметров) применяют усилители постоянного тока, построенные по
схеме М-ДМ (модулятор – демодулятор), где М – модулятор; ДМ – демодулятор;
У∼ – усилитель переменного тока. Усилители переменного тока не пропускают
постоянную составляющую сигнала, а, следовательно, у них отсутствует дрейф
нуля, и имеют достаточно большой и стабильный коэффициент усиления. Это
позволяет повысить чувствительность и точность вольтметров. Для того чтобы
использовать такой усилитель в вольтметрах постоянного тока, необходимо
преобразовать постоянное измеряемое напряжение в переменное, один из
параметров которого (информативный параметр) был бы пропорционален
измеряемому напряжению. Такая процедура может быть реализована с помощью
амплитудно-импульсной модуляции.
Генератор управляет работой модулятора и демодулятора, представляющих собой в
простейшем случае аналоговые ключи, синхронно замыкая и размыкая их с некоторой
частотой задающего генератора. На выходе модулятора возникает однополярный
импульсный сигнал, амплитуда которого пропорциональна измеряемому напряжению.
Переменная составляющая этого сигнала усиливается усилителем У∼, а затем
выпрямляется демодулятором. Применение управляемого демодулятора (а не
обычного выпрямителя) делает вольтметр чувствительным к полярности входного
сигнала. Необходимость выпрямления обусловлена тем, что магнитоэлектрический
измерительный механизм чувствителен только к постоянной составляющей (среднему
значению) сигнала. При заданных и постоянных параметрах импульсов среднее
значение напряжения выходного сигнала пропорционально входному напряжению UСР
= kM kУ kДМ UX , где kM и kДМ коэффициенты преобразования модулятора и
демодулятора, kУ – коэффициент усиления усилителя, и следовательно, угол
отклонения указателя ИМ α = SU UСР = SU kM kУ kДМUX = kVUX, где ; kV – коэффициент
преобразования электронного вольтметра; UX – измеряемое напряжение. ┘
111
47. Электронные вольтметры постоянного тока без преобразования спектра
Может измерять мВ, В (не мкВ).
!Работает на нулевой частоте!
ППИ – переключатель пределов измерений. В данном случае в качестве ППИ –
делитель напряжения.
УПТ – усилитель постоянного тока (есть дрейф). Должен работать на линейном
участке.
Отсчет производится в м/э им.
Так как ток постоянный, то, следовательно, нет преобразования спектра.
┌Угол отклонения указателя измерительного механизма
α=kППИkУПТSUUX = kVUX,
где kППИ, kУПТ – коэффициенты преобразования (деления и усиления) соответственно
ППИ и УПТ; SU – чувствительность к напряжению измерительного механизма; kV –
коэффициент преобразования электронного вольтметра; UX – измеряемое напряжение.
Последовательное соединение делителя напряжения и усилителя является характерной
особенностью построения всех электронных вольтметров. Такая структура позволяет
делать вольтметры многопредельными с широким диапазоном измерений за счет
широкого изменения общего (kППИkУПТ) коэффициента преобразования. Недостатком
УПТ, используемого в вольтметрах постоянного тока, являются нестабильность его
работы, проявляющаяся в изменении коэффициента усиления kУПТ и в т. н. «дрейфе
нуля» (самопроизвольном изменении выходного сигнала). В связи с этим применяют
УПТ с небольшим коэффициентом усиления, что определяет невысокую
чувствительность вольтметров постоянного тока. Как правило, верхний предел
измерений не бывает ниже десятков или единиц милливольт. При этом обеспечивается
достаточно большое входное сопротивление вольтметра.
Для уменьшения влияния нестабильности УПТ в вольтметрах постоянного тока
предусматривается возможность регулировки перед измерением «нуля» и
коэффициента усиления. ┘
112
1. Амплитуда
2. Форма
3. Частота
48. Электронные вольтметры переменного тока
Что хотим измерить?
1. Амплитуду
2. Среднее значение
3. Действующее значение
Надо смотреть паспорт, что измеряет прибор!!!
┌ Такие вольтметры состоят из преобразователя
переменного напряжения в постоянное, усилителя
и магнитоэлектрического измерительного
механизма.
Рисунок 9.8 Возможны
две обобщенные
структурные схемы
вольтметров переменного
тока (рис. 9.8),
различающиеся своими
характеристиками. В вольтметрах по схеме рис. 9.8, а измеряемое напряжение их
сначала преобразуется в постоянное напряжение, которое затем подается на УПТ и
ИМ, являющиеся, по существу, вольтметром постоянного тока. Преобразователь Пр
представляет собой малоинерционное нелинейное звено (см. далее), поэтому
вольтметры с такой структурой могут работать в широком частотном диапазоне (от
десятков герц до 103 МГц). Для уменьшения влияния распределенных емкостей и
индуктивностей входного кабеля и входной цепи прибора преобразователи обычно
выполняют в виде выносных узлов-пробников. В то же время указанные недостатки
УПТ и особенности работы нелинейных элементов при малых напряжениях не
позволяют делать такие вольтметры высокочувствительными. Обычно их верхний
предел измерений при максимальной чувствительности составляет десятки − единицы
милливольт. В вольтметрах, выполненных по схеме 9.8, б, благодаря
предварительному усилению удается повысить чувствительность. Однако создание
усилителей переменного тока с большим коэффициентом усиления, работающих в
широком диапазоне частот, − достаточно трудная техническая задача. Поэтому такие
вольтметры имеют относительно низкий частотный диапазон (5…20МГц); верхний
предел измерений при максимальной чувствительности составляет 28 десятки или
сотни микровольт. В зависимости от вида преобразователя переменного напряжения в
постоянное отклонения указателя измерительного механизма вольтметров могут быть
пропорциональны амплитудному (пиковому), среднему (средневыпрямленному) или
действующему значениям измеряемого напряжения. В связи с этим вольтметры
называют соответственно вольтметрами амплитудного, среднего или действующего
значения (см. примеры). Однако независимо от вида преобразователя шкалу
вольтметров переменного тока, как правило, градуируют в действующих значениях
напряжения синусоидальной формы.
┘
113
Широкополосные электронные приборы
Выпрямитель-усилитель (В-У)
УПТ – усилитель постоянного тока.
В – выпрямитель. В качестве выпрямителя можно взять диод, но берут детектор.
Д – детектор – предназначен для преобразования переменного напряжения в
постоянное. Основная функция – выпрямлять
114
Усилитель-выпрямитель (У-В)
Примечание: такие электронные вольтметры обладают погрешностью, связанной с
формой кривой сигнала на входе, тк почти все электронные вольтметры градуируются
в действующих значениях синусоидального сигнала.
Эту погрешность можно уменьшить специальными расчетами.
Пример 1
Umax=KA*U
Uвх=КА*Uп/ КА. КА*Uп в числителе из-за АД.
Пример 2:
𝑈𝑈вх =
𝑈𝑈п
1,11
∗ Кср ,
𝑈𝑈п
1,11
− среднее
Пример 3:
115
1
𝑈𝑈 = � � 𝑢𝑢2 𝑑𝑑𝑑𝑑 − действ. значение
Т
Если в электронном вольтметре стоит детектор действующего значения, то Uп=Uвх.
Uвх
А)
Б)
КА=1,41
Кср=1,11
КА=1
Кср=1,0
КА=…
Кср=…
В)
49. Селективные вольтметры
Селективные вольтметры предназначены:
• Измерение слабых сигналов на уровне больших помех
• Для измерения гармоник и спектра (позволяют выявить гармоники сигнала)
2Δf<<f0 (узкополосные высокочастотные приборы)
𝑓𝑓0 – частота настройки
2Δf – полоса пропускания
(кусочно-непрерывная функция)
116
ВУ – входное устройство (чаще всего усилители широкополосные)
СМ – смеситель – нелинейный элемент (смешивает Ux* и Uг)
Г – гетеродин (высокочастотный генератор)
Генератор – прибор с положительной обратной связью
𝑈𝑈см − самый странный сигнал, не синусоида, может содержать гармоники
𝑓𝑓г +𝑓𝑓𝑥𝑥
1
𝑓𝑓 −𝑓𝑓
𝜔𝜔0 =
𝑈𝑈см : � г 𝑥𝑥
𝐿𝐿𝐿𝐿
√
2𝑓𝑓г − 𝑓𝑓𝑥𝑥
…
Промежуточная частота: 𝑓𝑓п = 𝑓𝑓𝑥𝑥 − 𝑓𝑓г
ИУ – избирательный усилитель
Д – детектор. Цель – выпрямление
Как посмотреть форму сигнала?
Гармоники:
2
1? 𝐴𝐴1 ? 𝑓𝑓1 ?
4
3? 𝐴𝐴3 ? 𝑓𝑓3 ?
6
5? 𝐴𝐴5 ? 𝑓𝑓5 ?
8
7? 𝐴𝐴7 ? 𝑓𝑓7 ?
…………………….
Работа схемы:
1. Крутим гетеродин (меняется 𝑓𝑓п = 𝑓𝑓𝑥𝑥 − 𝑓𝑓г = 𝑣𝑣𝑣𝑣𝑣𝑣),
до тех пор пока 𝑓𝑓п = 𝑓𝑓0 ‼!
Может показать амплитуду первой гармоники А1
• Крутим, пока 𝑓𝑓х = 𝑓𝑓0 опять, записываем А3, ….. и т.д. (показания прибора
увеличиваются в определенное количество раз (в 3 раза – 3 гармоника)).
Омметр на малые сопротивления
Идея: Rx? (10 Ом)
117
Г – генератор (не высокочастотный)
R0 – ограничительное сопротивление (поскольку Rx может быть мало, R0
не дает закоротить генератор)
У~ - усилитель переменного тока
СД – синхронный детектор (обладает высокой помехозащищенностью) – для
выпрямления
Uопорн – особенность схемы СД
Особенности:
-У не имеет дрейфа
-могут возникнуть термоЭДС и другие плохие вещи
50. Детекторы электронных вольтметров
Д – детектор – предназначен для преобразования переменного напряжения в
постоянное. Основная функция – выпрямлять
Пример 1
Umax=KA*U
Uвх=КА*Uп/ КА. КА*Uп в числителе из-за АД.
Пример 2:
118
𝑈𝑈вх =
𝑈𝑈п
1,11
∗ Кср ,
𝑈𝑈п
1,11
− среднее
Пример 3:
1
𝑈𝑈 = � � 𝑢𝑢2 𝑑𝑑𝑑𝑑 − действ. значение
Т
Если в электронном вольтметре стоит детектор действующего значения, то Uп=Uвх.
Uвх
А)
Б)
КА=1,41
Кср=1,11
КА=1
Кср=1,0
КА=…
Кср=…
В)
Некоторые схемы детекторов
1. АД
А) с открытым входом
Б) с закрытым входом (не пускает постоянную составляющую)
119
Надо: URн=Uвх max !!!
𝜏𝜏з = 𝐶𝐶 ∗ (𝑅𝑅пр + 𝑅𝑅𝑖𝑖 )
𝜏𝜏раз = 𝐶𝐶 ∗ 𝑅𝑅н
𝜏𝜏раз ≫ 𝜏𝜏з
2. ДСЗ
Двух полупериодная схема
м/б схема 2 диода + 2 сопротивления (часто, но не всегда).
Диод более чувствителен к помехам, чем сопротивление.
3. ДДЗ
1) Квадратор
2) Интегратор
3) Извлекатель корня (не существует, эту операцию выполняют с помощью
градуировки).
120
51. Электронный однолучевой осциллограф с электростатическим управлением
луча. Упрощенная структурная схема
┌Электронно-лучевые (электронные) осциллографы предназначены для визуального
наблюдения, измерения и регистрации электрических сигналов. Возможность
наблюдения меняющихся во времени сигналов делает осциллографы чрезвычайно
удобными при определении различных амплитудных и временных параметров
наблюдаемых сигналов. Важными достоинствами осциллографов являются широкий
частотный диапазон, высокая чувствительность и большое входное сопротивление.
Всё это обусловило их широкое практическое применение.
В основе работы любых электронных осциллографов лежит преобразование
исследуемых сигналов в видимое изображение, получаемое на экране электроннолучевой трубки.┘
1. Является регистрирующим устройством. Показывает зависимость сигнала от
времени: x = f(t)
2. Функциональная зависимость: x = f(y)
А)
Б)
3. Измерение параметров (осциллограф имеет класс точности)
В)
Г)
Основная часть осциллографа - Экран из
электронно-лучевой трубки.
Измеряет несколько сигналов (многоканальные
многолучевые осциллографы).
Для того, чтобы посмотреть несколько сигналов,
берут однолучевой осциллограф с внешним
коммутатором
121
Толщина линий 0,7 мм.
Сверх-сверх упрощенная структурная схема осциллографа
Канал Z – для управления яркостью
Канал Y – канал вертикального отклонения
Канал X – канал горизонтального отклонения
БП – блок питания
ЭЛТ – электронно-лучевая трубка
1. Средства измерения ( ЦВ - цифровой вольтметр , Цf - цифровой частотомер )
2. Устройства, улучшающие метрологические характеристики (МП –
микропроцессоры)
3. Устройства для улучшения процесса управления (МП):
Устройства калибровки
• Калибратор по амплитуде
• Калибратор по частоте
• Калибровочная сетка
Сверх упрощенная структурная схема осциллографа
122
Н – накал, от БП переменного напряжения нагревается Н, который разогревает К
(катод)
М(С-сетка) – модулятор
1А, 2А – аноды
Вся система питается от БП, аноды питаются положительным напряжением.
X и Y откладывают по вертикали и горизонтали, поэтому на них должно быть
напряжение.
R1 – яркость, меняем потенциал по сетке, изменяем количество электронов,
доходящих до экрана.
R2 – фокус.
123
Упрощенная схема осциллографа
Обозначения на схеме:
БП – блок питания (для возможности нагрева катода)
Тракт вертикального отклонения (канал вертикального отклонения) или канал Y:
АY – активатор (аттенюатор) или делитель напряжения канала Y
ПУY – предварительный усилитель по каналу Y (для того, чтобы не «испортить
сигнал, подаваемый на вход канала Y, к данному блоку предъявляются требования
линейности частотных, амплитудных и фазовых характеристик)
ЛЗ – линия задержки (необходима, естественно, для задержки подачи входного
сигнала на пластины YY для исключения возможности опережения развёртки (короче,
чтобы развёртка запускалась раньше, чем сигнал попадёт на пластины отклонении
YY))
ОУY – окончательный усилитель по каналу Y (это каскад для симметрирования
напряжения относительно нулевой линии (из-за этого выводов у этого блока три, один
из которых земля))
Чтобы было на так,
, а так
ИКН – источник калибровочного напряжения
124
Если сделали калибровку, то есть ручка 𝑚𝑚𝑦𝑦 =
3
1 𝑚𝑚𝑚𝑚
𝑆𝑆𝑦𝑦 𝑚𝑚𝑚𝑚
30
300
Тракт горизонтального отклонения (канал горизонтального отклонения) или
канал X:
БС – блок синхронизации, позволяет получить на экране неподвижное изображение
(Tразвертки=nTсигнала, где n=1,2,3…), работающий в трёх режимах:
• Внутренняя синхронизация (от канала Y (!))
• Синхронизация от сети (частота 50 Гц)
• Внешняя синхронизация (подаём сигнал сами)
БР – блок временной развёртки, посмотреть сигнал, поданный на Y во времени,
работающий в двух режимах:
• Ждущий режим – запускается только лишь, когда приходит сигнал. Это
необходимо для того, чтобы наблюдать однократные сигналы или сигналы с
большой скважностью.
• Непрерывный режим
Канал Y имеет больший коэффициент усиления, чем Х.
ПУX – предварительный усилитель по каналу X
ОУX – окончательный усилитель по каналу X (то же самое что ОУY, только по X)
Аx – активатор (аттенюатор)
┌Канал X может работать в двух режимах:
• Переключатель П3 находится в положении 1 – режим временной развёртки
• Переключатель П3 находится в положении 2 – режим измерения сигнала,
поданного на вход X┘
Режим развёртки обычно используется для наблюдения сигнала, поданного на вход Y
на экране осциллографа.
Если развёртка выключена, то осциллограф позволяет либо измерять сигналы,
поданные на вход X, либо наблюдать функциональные зависимости типа 𝑦𝑦 = 𝑓𝑓(𝑥𝑥), но
для этого необходимо подать сигнал на оба входа: и на вход Y и на вход X.
Канал Z или канал управления яркостью, присутствующий в современных
осциллографах, состоит из:
СИП – схема изменения полярности
УZ – усилитель по каналу Z
Этот канал подключен к сетке-модулятору.
Современные приборы снабжены различными калибраторами, такими как калибратор
амплитуды (на схеме - КА), устанавливающий градуированное значение канала Y
125
(проще говоря, масштаб по Y) и калибратор длительности (КД), устанавливающий
масштаб по временной оси.
Так же в современных осциллографах на экране присутствует калибровочная сетка,
такая:
Работа осциллографа:
Простейшая однолучевая трубка (ЭЛТ) представляет собой стеклянный баллон, из
которого откачан воздух и в котором расположены (смотри рисунок), подогреваемый
накалом Н, катод К, сетка (или модулятор) С(М), фокусирующий анод А1, ускоряющий
анод А2, две пары взаимно перпендикулярных отклоняющих пластин YY и XX
(вертикальные и горизонтальные пластины). Внутренняя поверхность дна баллона
(экран) покрыта люминофором, веществом, способным светиться под действием
бомбардировки электронами. Совокупность электродов К, С(М), А1, А2 называют
электронной пушкой (ЭП). Конструктивно эти электроды выполнены в виде цилиндров,
расположенных по оси трубки. Электронная пушка излучает узкий пучок электронов –
электронный луч. Для этого на электроды пушки подают напряжение особым образом.
Интенсивность электронного луча регулируется путём изменения отрицательного,
относительно катода, напряжения на сетке (модуляторе), что приводит к изменению
яркости свечения люминофора. Напряжение («хорошее», большее, положительное
напряжение для уменьшения разброса заряженных частиц) на первом аноде фокусирует
поток электронов в узкий луч, позволяющий получить на экране трубки светящееся
пятно малого радиуса. Для ускорения электронов до скорости, необходимой для
свечения люминофора, на второй анод подаётся высокое положительное напряжение
(электрон – отрицательная частица; противоположно заряженные частицы
притягиваются с высокой скоростью). Сформированный электронный луч проходит
между парами отклоняющихся пластин YY и XX и под действием напряжений,
приложенных к этим пластинам, отклоняется, соответственно, по осям координат Y и
X, вызывая смещение светящегося пятна на экране трубки.
При исследовании быстропротекающих процессов с малой частотой повторения или
однократных импульсов электронный луч не успевает возбудить в достаточной мере
люминофор, и яркость свечения может оказаться недостаточной. Поэтому в
современных электронно-лучевых трубках применяют дополнительное ускорение
электронов при помощи третьего анода А3, подавая на него большое положительное
напряжение.
Погрешность у осциллографов составляет 6%, что довольно много. Дело в том, что
даже простая точка, в сравнении с размерами экрана электронно-лучевой трубки имеет
весьма большие габариты. Кстати, размеры экрана современных осциллографов
начинаются с семидесяти миллиметров и выше. Тип люминофора определяет цвет
свечения экрана. Обычно находят применение трубки с зелёным цветом свечения (как
в лаборатории). А, например, для удобства фотографирования изображения с экрана
ЭЛТ, применяют трубки с голубым свечением люминофора.
126
В современных осциллографах применяют также более сложные, в частности,
многолучевые трубки для наблюдения сразу двух и более сигналов, трубки с линией
бегущей волны для наблюдения сверхвысокочастотных колебаний и др.
52. Узлы электронного осциллографа и требования к ним
Тут все об осциллографе, все вопросы билетов, связанного с ним (51-56).
Т.е. все его блоки, развертка, отклонение, синхронизация, калибровка.
53. Канал вертикального отклонения осциллографа
Тут развертка выключена, форма сигнала не видна.
Пластины вертикального отклонения YY:
Подаем следующие сигналы:
в) в нашем случае был волнистый сигнал (как синус, но с ямкой)
На экране увидим следующее:
ly=Uy/my, Uy= ly* my (my – известно)
причём, SТ Y – чувствительность трубки по вертикали, [мм/В]; UY – напряжение,
приложенное к пластинам, [В]; А – амплитуда сигнала, [В] (для б) синусоиды и в)
меандра).
Чувствительность SТ трубки – отклонение луча на экране ЭЛТ, вызванное
напряжением UY, приложенным к отклоняющим пластина. Обычно чувствительность
составляет порядка 0,5 ÷ 5 [мм/В].
Примечание:
При чувствительности трубки SТ Y в 0,5 [мм/В] и высоте экрана 70 миллиметров,
напряжение UY, необходимое для продвижения точки по всему экрану от края до края
(по оси Y) должно быть равно ста сорока вольтам, что весьма велико.
Вывод: 1) форма сигнала на экране не наблюдается. В случае подачи
периодического сигнала (с двумя полуволнами) – на экране появляется линия, равная
двум амплитудам входного сигнала.
2) Из примечания ясно, что большие сигналы можно подавать прямо на пластины
отклонения, а не на вход
127
54. Канал горизонтального отклонения осциллографа
Исследование сигналов проходящих через пластины горизонтального отклонения
даёт те же результаты и выводы.
Тут развертка выключена, форма сигнала не видна.
Пластины горизонтального отклонения XX:
Подаем следующие сигналы:
в) в нашем случае был волнистый сигнал (как синус, но с ямкой)
На экране увидим следующее:
lх=Uх/mх, Uх= lх* mх (mх – известно)
причём, SТ X – чувствительность трубки по горизонтали, [мм/В]; UX – напряжение,
приложенное к пластинам, [В]; А – амплитуда сигнала, [В] (для б) синусоиды и в)
меандра).
Чувствительность SТ трубки – отклонение луча на экране ЭЛТ, вызванное
напряжением UY, приложенным к отклоняющим пластина. Обычно чувствительность
составляет порядка 0,5 ÷ 5 [мм/В].
Примечание:
При чувствительности трубки SТ Y в 0,5 [мм/В] и высоте экрана 70 миллиметров,
напряжение UY, необходимое для продвижения точки по всему экрану от края до края
(по оси Y) должно быть равно ста сорока вольтам, что весьма велико.
Вывод: 1) форма сигнала на экране не наблюдается. В случае подачи
периодического сигнала (с двумя полуволнами) – на экране появляется линия, равная
двум амплитудам входного сигнала.
2) Из примечания ясно, что большие сигналы можно подавать прямо на пластины
отклонения, а не на вход
128
55. Понятие о развертке. Непрерывная и ждущая развертка
у
x
x
у
Uy = f(t) сигнал во времени.
Создаёт линейную временную развёртку для сигнала, подаваемого на вход канала Y.
Для получения изображения исследуемого сигнала, развёрнутого во времени,
необходимо смещать («развёртывать») луч по оси X c равномерной скоростью. Это
осуществляется подачей на отклоняющие пластины XX линейно изменяющегося
пилообразного напряжения
Up
tп
t0
Tp
Tp
t
Up = kt; k = const
tп<<t0
Tp = tп+t0; период развёртки
Up
tп
t0
t
tп – прямой ход луча (слева-направо)
t0 – обратный ход луча (справа-налево)
┌Идеально было бы, если бы tО = 0 и тогда ТР = tП. ДЛЯ того чтобы во время
обратного хода электронный луч не вычерчивал линии на экране осциллографа, его
гасят на это время путём подачи отрицательного напряжения на сетку (модулятор).
Исследование сигналов в широком диапазоне частот обеспечивается переключением
частоты пилообразного напряжения, предусмотренном в генераторе развёртки. Это
позволяет проводить наблюдения исследуемых сигналов в нужном масштабе времени.
Выходное напряжение генератора усиливается в усилителе горизонтальной развёртки
до значения, необходимого для управления электронным лучом в ЭЛТ и получения
изображения требуемого размера.┘
Пример 1. Uy = 0; Up вкл
За время tп, если осциллограф плохо отрегулировали пробегает полоса.
129
Tp = tп
Up
tп
t
Tp –var можно менять.
В осциллографах существуют два вида развёртки:
• Непрерывная, которая может иметь место быть вне зависимости от наличия
сигнала на входе Y
o и
• Ждущая, которая может иметь место быть только при наличии сигнала, поданного
на вход канала Y
На непрерывной развёртке при отсутствии сигнала на входе, электронный луч
просто «пробегает» некоторое расстояние по оси X «туда и обратно».
Ждущая же развёртка применяется в случае, когда есть желание пронаблюдать
однократный сигнал или периодический с повышенной скважностью.
Пример: Непрерывная
Развёртка включена
а)
б)
Tp выбирается из соответствия Tp=nTc
Слева – направо
Пример: Ждущий
130
Сигнал большой скважности
Непрерывная Развёртка:
а) Tp=Tc
б) Tp = τнепр
Ждущая развёрта:
в) Tp = τждущий
131
56. Понятие о синхронизации. Амплитуда синхронизации и частота
Tp= nTc - целое; заставляет генерировать Tp кратный
Амплитудная синхронизация
Идея: выработка ограниченного сигнала
Ас1 и Ас2 – мало отличаются.
Накладывается периодический сигнал.
Синхронизация от сети 50 Гц.
Пример fc (частота синхронизации).
БС работает в 3-х режимах.
Пример.
Пропустили фронт поэтому делают так: развёртку запускают раньше, для этого – ЛЗ.
Пример: измерить можно А = мкВ, В,мВ масштаб известен
132
Калибратор длительности градуирует в цифрах ось времени.
Калибратор меток
Примечание:
57. Общие сведения о цифровых (ЦИП) приборах. Методы построения АЦП.
Погрешности ЦИП
Системы счисления
Любое число в любой системе счисления может быть представлено в виде:
𝑁𝑁 = � 𝑎𝑎𝑖𝑖 ∗ ℎ𝑖𝑖−1
𝑖𝑖
h – основание сс
а – коэффициенты
h=2 => ai=0;1
Примеры 0÷ 9
1) 9=1 ∗ 23 + 0 ∗ 22 + 0 ∗ 21 + 1 ∗ 20 = 8 + 0 + 0 + 1 => 910 → 10012
2) 93810→11101010102 (неважно)
Состояние 0-1 легко реализовать технически (триггеры):
0 – нет сигнала
1- есть сигнал
h=10 ai=0…9 (10 шт)
Декатроны – устройства с десятью устойчивыми состояниями
h=60 ai=0…..59 (60 шт)
938=15 ∗ 601 + 38 ∗ 600 (неважно)
133
Пример позиционного кода:
938
(30 шт) 0 ÷ 999
Различают коды с различными весовыми коэффициентами
Пример:
9→1001
23 + 22 + 21 + 20
8 − 4 − 2 − 1 ← весовые коэффициенты
Другие весовые коэффициенты:
2–4–2–1
9=2+4+2+1
Число 5:
А) 5=2+2+1
Б) 5=4+1
Коды с такими весовыми коэффициентами (дефект – неоднозначность показаний)
широко используются, тк реализуются легче, чем с коэффициентами 8 – 4 – 2 – 1
Цифровые измерительные приборы (ЦИП)
Достоинства:
6) Высочайшая точность
7) Высокая чувствительность
8) Универсальность
9) Широкий частотный диапазон
10)
! возможность работы с компьютером
Недостатки:
6) Требуют источника питания
7) Требуют большого прогрева (больше часа)
8) Дорогие
9) Напичканы многими приборами, схемами
10) Обладают сравнительно невысокой надежностью
АУ – аналоговое устройство
АЦП – аналогово цифровой преобразователь
134
Примечание: помимо чисто аналоговых и чисто
цифровых существуют дискретно- аналоговые приборы
и дискретно-цифровые.
У этих приборов отсчет воспринимается как аналоговый,
кроме того, у него имеется чисто цифровой отсчет.
Методы построения АЦП (это было в 21 вопросе)
1) Метод считывания
2) Метод последовательного счета
3) Метод сравнения вычитания – наиболее распространенный
Метод считывания
Идея:
Прибор определяет, к какому уровню квантования ближе сигнал.
┌При этом методе происходит одновременное сравнение измеряемой величины X с
известными величинами X1, X2, X3, …, значения которых равны уровням квантования.
Известная величина, равная измеряемой Xi = X(tИ), даёт номер отождествляемого
уровня квантования, в соответствии с которым образуется код, то есть значение
измеряемой величины.┘
Технический шаблон
Метод последовательного счета
(Времяимпульсный вольтметр)
Сигнал определяется по количеству
ступеней (h=const)
┌При этом методе происходит
последовательное во времени сравнение
измеряемой величины X с известной
величиной Xi (ступенька),
изменяющейся (возрастающей или
убывающей) во времени скачками,
причём каждый скачок соответствует шагу (ступени) квантования h по уровню. Число
ступеней, при котором наступает равенство X = Xi(tИ) (c некоторой погрешностью),
равно номеру отождествляемого уровня квантования. В процессе сравнения
образуется код, соответствующий номеру отождествляемого уровня квантования.
Возможно инверсное преобразование, при котором известная постоянная величина
сравнивается с равномерно квантуемой величиной, функционально связанной с
измеряемой величиной.┘
Метод сравнения вычитания
Квантованную функцию строят по определенному алгоритму в соответствии с кодом.
135
┌При этом методе происходит
последовательное во времени сравнение
измеряемой величины X c известной
квантованной величиной Xi ,
изменяющейся во времени скачками по
определённому правилу (исключая
единичную систему счисления). Значение
известной величины при которой наступает
равенство X = Xi(tИ), соответствует номеру
отождествляемого уровня квантования.
Код, образуемый в процессе этой операции, соответствует отождествляемому
уровню.┘
Погрешности
Существует 3 метода квантования:
- отнесение к нижнему уровню
- отнесение к верхнему уровню
- отнесение к ближайшему уровню
1) Отнесение к нижнему уровню
Непрерывный сигнал квантуют по уровню (строят квантовую функцию)/
Эти уровни нумеруются с нуля, причём уровень с номером нуль – это уровень оси
абсцисс. На каждом уровне все значения равны (т.к. уровни - это параллельные
линии). Значит, если мы хотим узнать, что происходит на уровне N, используем
формулу 𝑁𝑁 ∗ ℎ.
h – шаг квантования (и разрешающая способность) = const.
Уровни квантования кодируются, т.е. переводятся в электрический сигнал.
Ошибка, то есть разность между аналоговой и квантованной функцией существует и
равна шагу квантования.
∆Хдискр = Хкв − Х
2) Отнесение к верхнему уровню
𝛥𝛥𝑋𝑋дискр−ти 𝑀𝑀𝑀𝑀𝑀𝑀 = −ℎ
𝛥𝛥𝑋𝑋дискр−ти 𝑀𝑀𝑀𝑀𝑀𝑀 = ℎ
136
3) Отнесение к ближнему уровню
Обратите внимание на минус в погрешности для отнесения к нижнему уровню и на
плюс в погрешности для отнесения к верхнему уровню.
Погрешность можно уменьшить аж до полушага квантования, если провести
квантованную функцию по центру тяжести аналоговой функции.
∆Хдискр = ±ℎ/2
1) Отнесение к нижнему уровню
2) Отнесение к верхнему уровню
3) Отнесение к ближнему уровню
Чтобы уменьшить погрешность надо уменьшать шаг квантования или увеличивать
число уровней квантования (а лучше и то и другое вместе).
137
58. Вольтметр на принципе считывания
Это вольтметр постоянного тока.
СУ – сравнивающее устройство
ИОН – источник образцового напряжения (i=const; напряжения отличается на
постоянную величину (шаг квантования))
ПКК – преобразователь кода в код
ЦОУ – цифровое отсчетное устройство (на светодиодах, на индикаторных лампах)
Самые быстродействующие устройства
На вход подаются 2 сигнала: хорошо известный образцовый с высокой точностью и
искомый сигнал и сравниваются:
Uвх>=Uoi=> сигнал 1
Наоборот => сигнал 0
Работа схемы:
Одновременно на все входы сравнивающих СУ устройств подаётся неизвестное, но
желаемое быть измеренным напряжение UX, на вторые входы СУ (правые) подаётся
напряжение от образцового источника, причём на всё СУ – разное. На выходе схемы
располагается преобразователь кода в код. СУ срабатывает, если на оба входа подано
одно и тоже напряжение. На выходе, если СУ сработало, вырабатывается сигнал,
соответствующий логической единице.
ПКК получил сигналы от сравнивающих устройств, преобразовал их в коды для
цифрового отсчётного ЦОУ устройства, чтобы измеряющий (человек) понял
результат.
Этот прибор хорош своим быстродействием, но в тоже время, данное устройство
очень сложно в исполнении и имеет в себе множество элементов.
Прибор реализовывает аналого-цифровой метод считывания.
138
59. Времяимпульсный цифровой вольтметр
Реализует метод последовательного счета
Схема обладает невысокой помехозащищенностью
Во Времяимпульсном вольтметре применяются 2 преобразования:
• Аналоговое
Аналоговая величина преобразуется в интервал времени: A →Ux→ tx!!!
Есть сравнивающее устройство
ГЛИН – генератор линейно изменяющегося напряжения
Uглин=k*t
K=const
Ux1=k*tx1
Недостатки в преобразовании:
-СУ должно обладать высокой чувствительностью
- K должно быть const, но это не так, тк ГЛИН обладает малой
нелинейностью.
• Цифровое
Идея: надо иметь источник импульса с точной высокой частотой
(f0=const), например, кварцевый генератор.
Число импульсов считаем: N=tx/T0=tx*f0
-должна быть высокая частота (чем больше импульсов вмещается в интервал времени,
тем лучше)
139
Как показано на рисунке выше, при измерении возникают 4 проблемы: погрешность до
старта ∆t1, погрешность после старта, погрешность до остановки ∆t2, погрешность после
остановки.
Ликбез
Сверхупрощенная схема Времяимпульсного вольтметра
Сброс – для чистоты (от 0)
УК – устройство управления ключом (триггер)
ГОЧ – генератор образцовой частоты
ПУ – пересчетное устройство/счетчик импульсов
140
ЦОУ – цифровое отсчетное устройство
УУ+УС – устройство управления и синхронизации
Ключ замыкается – интервал времени заполняется
импульсами.
Кодоимпульсный вольтметр
Основан на методе сравнения.
УП – устройство преобразования
ЦАП – цифроаналоговый преобразователь
Принцип работы – как у предыдущей схемы
Цифровые приборы хороши разрядностью
141
Приложение
Это было в лекциях, но я не знаю, куда это пихать
Оценка погрешностей косвенных измерений
Косвенные измерения – измерения, в которых искомое значение результата
измерений находят на основе прямых измерений других величин, функционально
связанных с искомой величиной.
y = F( 𝑥𝑥1 , 𝑥𝑥2 ,….., 𝑥𝑥𝑛𝑛 )
y – искомая величина
𝑥𝑥𝑖𝑖 - значение величины, полученных с помощью прямых измерений.
Особенностью косвенных измерений является одновременное измерение аргументов,
что позволяет получить значение измеряемой величины к конкретному моменту
времени.
Измеряют значения величин с погрешностью.
Результат косвенных измерений получается подстановкой оценок аргументов в
уравнение.
Для нахождения границ абсолютной погрешности косвенных измерений
воспользуемся формулой полного дифференциала, заменив его на приращение, т.е. на
абсолютную погрешность:
𝜕𝜕𝜕𝜕
𝜕𝜕𝜕𝜕
𝜕𝜕𝜕𝜕
∆y= ∆𝑥𝑥1 + ∆𝑥𝑥2 +…..+ ∆𝑥𝑥𝑛𝑛
𝜕𝜕𝜕𝜕
𝜕𝜕𝑥𝑥𝑖𝑖
𝜕𝜕𝑥𝑥1
𝜕𝜕𝑥𝑥2
𝜕𝜕𝑥𝑥𝑛𝑛
–частная производная F по аргументу 𝑥𝑥𝑖𝑖
∆𝑥𝑥𝑖𝑖 - абсолютная погрешность измерения аргументов
Функция
абс. погрешность
относ. погрешность
∆𝑥𝑥 +∆𝑥𝑥
y= 𝑥𝑥1 +𝑥𝑥2
∆y=± (∆𝑥𝑥1 +∆𝑥𝑥2 )
𝛿𝛿𝑦𝑦 = 1 2 *100
𝑥𝑥1 +𝑥𝑥2
y= 𝑥𝑥1 -𝑥𝑥2
∆y=± (∆𝑥𝑥1 +∆𝑥𝑥2 )
y= 𝑥𝑥1 *𝑥𝑥2
∆y=± (∆𝑥𝑥2 𝑥𝑥1 +∆𝑥𝑥1 𝑥𝑥2 )
y= 𝑥𝑥1 /𝑥𝑥2
∆𝑥𝑥2 𝑥𝑥1 +∆𝑥𝑥1 𝑥𝑥2
∆y=± (
)
𝑥𝑥2 2
∆𝑥𝑥1 +∆𝑥𝑥2
*100
∆𝑥𝑥1 ∆𝑥𝑥2
)*100
∆𝑥𝑥1 ∆𝑥𝑥2
)*100
𝛿𝛿𝑦𝑦 =
𝛿𝛿𝑦𝑦 =(
𝛿𝛿𝑦𝑦 =(
𝑥𝑥1 −𝑥𝑥2
𝑥𝑥1
𝑥𝑥1
+
+
𝑥𝑥2
𝑥𝑥2
Оценка неопределённости измерений
Неопределённость – параметр, связанный с результатом измерений и
характеризующий рассеяние значений, которые можно приписать измеряемой
величине.
Этим параметром может быть так называемое стандартное отклонение
(ср.квадратическая погрешность результата измерений) или кратное ему число или
ширина доверительного интервала.
Важно различать погрешность и неопределённость
Погрешность может иметь единственное значение. Значение погрешности можно
учесть, как поправку к результату измеренной величины.
142
Неопределённость представляется в виде интервала значений и не может быть
использована для улучшения результатов измерений.
Если известны неопределённости в виде стандартных отклонений из-за влияния
возможных мешающих факторов (изменения окружающей среды, погрешности СИ и
других источников), то определяют суммарную неопределённость.
𝑈𝑈𝑐𝑐 (𝑦𝑦) = �𝑈𝑈(𝑎𝑎)2 + 𝑈𝑈(𝑏𝑏)2 +. . . — для моделей влияния источников неопределённости
на результат изменения в виде суммы или разности.
U(a), U(b) —СКО факторов a, b, …
𝑈𝑈𝑐𝑐 (𝑦𝑦) = 𝑦𝑦��
𝑈𝑈(𝑎𝑎) 2
𝑎𝑎
� + |𝑈𝑈(𝑏𝑏)/𝑏𝑏|2 +. . . — для моделей влияния неопределённости на
результат измерения в виде произведения или дроби.
𝑈𝑈𝑐𝑐 (𝑦𝑦) — неопределённость результата изменения.
с – стандартная.
U(a), U(b) – неопределенность в виде стандартов отклонения в виде различных
источников.
Полученную стандартную неопределённость умножают коэффициент охвата k для
получения расширенной неопределённости, указывающей интервал, в котором
заключена большая часть распределения значений, приписанных измеряемой
величине с достаточным основанием.
Для большинства применений рекомендуется коэффициент охвата k = 2.
Например, если распределение нормальное, то k=2 при доверительной вероятности
P=95% приводит к интервалу, содержащему примерно 95% всех значений измеряемой
величины.
Место измерений в информационных технологиях
Какие линии связи бывают:
1) Проводная
2) Телесвязь
3) Радиосвязь
4) Оптоэлектроника
В канале связи напихано много устройств (измерительных устройств, устройств
преобразователей, память, устройств управления).
143
144