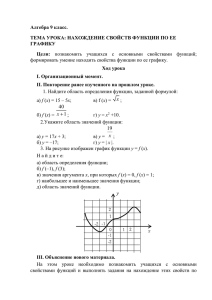
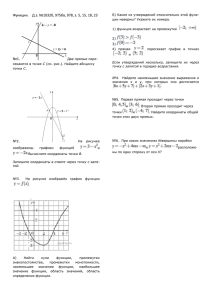
1. Функция задана графиком на отрезке [- 5; 3]. Укажите множество значений этой функции 2. Укажите число нулей функции, изображенной на рисунке, на промежутке (0; + ∞). 1). 4; 2). 5. 3). 6; 4). 2. у у х 3 -5 2 1,7 0 -1 х 3 х х х х 0 -2 у = f(x) 4. Функция у = f (x) определена на промежутке (– 6; 3). Укажите точку максимума функции у = f (x) на промежутке (– 6; 3). 3. Сколько промежутков возрастания имеет функция, график которой изображен на у рисунке? у х 0 у = f (x) y 1 –6 1 5. Функция задана графиком. Укажите промежуток, на котором она принимает только положительные значения. 0 1 x 0 1 3 х Задача урока: • Научиться описывать свойства функции по графику. План описания свойств функции: 1.Область определения: 2.Область значений (множество значений функции): 3.Чётность: 4.Пересечение с осями координат (нули функции): 5.Промежутки возрастания и убывания: 6.Наибольшее и наименьшее значения функции: 7.Промежутки знакопостоянства: Свойства функции: 10 1.Область определения: Х є [-3;3] у 9 2.Область значений: У є [0;9] 7 3.Чётность: f(x)=f(-x), значит функция чётная (ось симметрии – ось ординат, значит f(x) – чётная) 6 4.Пересечение с осями координат: (0; 0) 5 5.Промежутки возрастания и убывания: 4 f(x) возрастает на промежутке (0; 3); f(x) убывает на промежутке (-3; 0) 8 3 6.Наибольшее и наименьшее значения функции: min: f(0)=0; max: f(-3)=9, f(3)=9 7.Промежутки знакопостоянства: f(x)>0 при х є [-3; 0), (0; 3] 2 х 1 0 -4 -3 -2 -1 0 1 2 3 4 Перечислите свойства функции. 8 у 6 4 2 х 0 -12 -10 -8 -6 -4 -2 0 -2 -4 -6 -8 -10 2 4 6 8 10 12 Свойства функции: • • • 8 6 • 4 2 0 -12 -10 -8 -6 -4 -2 0 -2 х 2 4 6 8 10 12 • • • -4 -6 -8 -10 • Область определения: Х є [-10; 10]; Область значений: У є [-8; 6,2]; Чётность: f(x)‡f(-x), значит функция не является чётной; f(-x)‡-f(x), значит функция не является нечётной; Пересечение с осями координат: с осью абсцисс: (-8;0), (-3;0), (4;0), (8;0); с осью ординат: (0;-6); Промежутки возрастания: (-10; -5), (0,2; 6,2); Промежутки убывания: (-5; 0,2), (6,2; 10); Наибольшее и наименьшее значения функции: min: f(-10)=-8 ; max: f(6,2)=6,2; Промежутки знакопостоянства: f(х)<0 при хє[-10;-8), (-3;4), (8;10]; f(х)>0 при хє(-8;-3), (4;8).