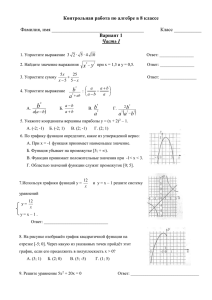
Административная контрольная работа по математике
(аудит) для 7 класса за 1 полугодие.
Учебники «АЛГЕБРА – 7» Мерзляк А.Г., Полонский В.Б.,
Якир М.С., «ГЕОМЕТРИЯ 7-9» Атанасян Л.С., Бутузов В.Ф.
Составитель: Тимакова Д. С., учитель математики.
Работа состоит из двух частей.
Часть А содержит 10 заданий базового уровня, задания с
выбором ответа.
Часть В содержит 3 задания, требующее записать решение и
ответ.
Обучающиеся должны
продемонстрировать знания, умения и навыки за 7 класс:
умение находить значение выражения, раскрывать скобки и
приводить подобные слагаемые, решать уравнения, умение
работать со степенями, приводить одночлен к
стандартному виду, упрощать выражения, знать начальные
геометрические сведения.
Ответы:
ва
ри
ан
т
1
А А
1 2
А
3
А
4
А
5
А
6
А
7
А
8
А
9
А
10
В
1
б
в
б
а
б
а
а
б
а
б
(1;2) 6
2
а
г
б
б
а
в
б
а
в
б
(2;1) 7
В
3
Критерий оценивания:
Часть «А» - 1балл за каждое задание.
Часть «В» - 2 балла за каждое задание.
Максимальное количество - 16 баллов.
Количество бал.
14-16
10-13
6-9
5-0
Отметка.
5
4
3
2
Итоговая контрольная работа по математике за 7 класс
Вариант I
А1. Найдите значение выражения 1,5 ∙ 62 − 23 .
а) 36
б) 46
в) 56
г) 66
А2. Упростите выражение −8𝑥 6 𝑦 ∙ (2𝑥 3 )5
а) −16𝑥 21 𝑦 б) −16𝑥 14 𝑦
в) −256𝑥 21 𝑦
а) 90°
б) 30°
в) 60°
г) 45°
А9. ∠1 = 480 , ∠2 = 1320 , ∠3 = 1220 . Какие из прямых,
изображенных на рисунке, являются параллельными?
а) 𝑎 и 𝑏
б) 𝑏 и 𝑐
в) 𝑎 и 𝑐
г) все прямые
параллельны
г) 256𝑥 21 𝑦
А3. Выполните умножение (𝑥 − 5𝑦)(3𝑦 + 2𝑥)
а) 7𝑥𝑦
б) 2𝑥 2 − 7𝑥𝑦 − 15𝑦 2
в) 2𝑥 2 − 13𝑥𝑦 − 15𝑦 2
г) 2𝑥 2 − 15𝑦 2
А4. Преобразуйте в многочлен (5𝑏 − 7𝑎)2
а) 25𝑏2 − 70𝑎𝑏 + 49𝑎2
б) 25𝑥 2 − 49𝑎2
в) 25𝑏2 − 35𝑎𝑏 + 49𝑎2
г) 5𝑏2 − 35𝑎𝑏 + 7𝑎2
А5. Функция задана формулой 𝑦 = 5𝑥 + 21. Определите
значение функции, если значение аргумента равно -3.
а) -36
б) 6
в) 36
г) -6
А6. Решите уравнение 6𝑥 − 14 = 4𝑥 + 7.
а) 10,5
б) 2,1
в)−10,5
г) 3,5
А7. Упростите выражение 2,5𝑦(4𝑦 − 2) − 5𝑦(2𝑦 − 8) и найдите
его значение при 𝑦 = −6.
а) -210
б) 235
в) -235
г) 245
А8. В прямоугольном треугольнике гипотенуза равна 10 см, а
один из катетов 5 см. Найдите наименьший из углов данного
треугольника.
А10. Один из смежных углов больше другого на 20⁰. Найдите
величины этих углов.
а) 65° и 115°
б) 80° и 100°
в) 25° и 155°
г) 40° и 140°
Часть В.
11𝑥 + 8𝑦 = 27
.
5𝑥 − 16𝑦 = −27
В2. Постройте график функции 𝑦 = 3𝑥 − 2. Пользуясь графиком,
найдите:
1) Значение функции, если значение аргумента равно 2;
2) Значение аргумента, если значение функции равно -5.
В3. В прямоугольном треугольнике 𝐴𝐵𝐶 угол между
биссектрисой 𝐶𝐾 и высотой 𝐶𝐻, проведенными из вершины
прямого угла 𝐶 равен 15⁰. 𝐴𝐵 = 12 см.Найдите сторону 𝐵𝐶, если
известно, что точка 𝐾 лежит между 𝐴 и 𝐻.
В1. Решите систему уравнений {
Итоговая контрольная работа по математике за 7 класс
а) 120°
Вариант II
А1. Найдите значение выражения 2,5 ∙ 24 − 72 .
а) -9
б) -19
в) -29
г) -39
А2. Упростите выражение −3𝑎5 𝑏2 ∙ (7𝑎3 )2
а) 21𝑎11 𝑏2
б) −21𝑎10 𝑏2
в) 147𝑎10 𝑏2
г) −147𝑎11 𝑏2
б) 90°
в) 150°
г) 130°
А9. ∠1 = 510 , ∠2 = 1390 , ∠3 = 1290 . Какие из прямых,
изображенных на рисунке, являются параллельными?
а) 𝑎 и 𝑏
б) 𝑏 и 𝑐
в) 𝑎 и 𝑐
г) все прямые
параллельны
А3. Выполните умножение (3𝑎 − 𝑏)(2𝑏 + 4𝑎)
а) 12𝑎2 − 2𝑎𝑏 − 2𝑏2
б) 12𝑎2 + 2𝑎𝑏 − 2𝑏2
в) 6𝑎𝑏 − 2𝑏2
г) 6𝑎𝑏 − 4𝑏
А4. Преобразуйте в многочлен (4𝑦 − 5𝑥)2
а) 16𝑦 2 − 20𝑥𝑦 + 25𝑥 2
б) 16𝑦 2 − 40𝑥𝑦 + 25𝑥 2
в) 4𝑦 2 − 25𝑥 2
г) 16𝑦 2 − 25𝑥 2
А5. Функция задана формулой 𝑦 = 6𝑥 − 14. Определите
значение функции, если значение аргумента равно -4.
а) -38
б) 38
в) 10
г) -10
А10. Один из смежных в 4 раза меньше другого. Найдите
величины этих углов.
а) 120° и 60°
б) 36° и 144°
в) 25° и 155°
г) 40° и 140°
А6. Решите уравнение 5𝑥 − 11 = 2𝑥 + 7.
Часть В.
а)
18
17
б) -6
в) 6
г)
11
7
А7. Упростите выражение 1,5𝑥 (4 − 6𝑥) − 3𝑥(𝑥 − 4) и найдите
его значение при 𝑥 = 1.
а) -18
б) 6
в) 12
г) 30
А8. В равнобедренном треугольнике высота, проведенная к
основанию, равна 7 см, а его боковая сторона равна 14 см.
Найдите наибольший угол данного треугольника.
9𝑥 + 13𝑦 = 31
.
18𝑥 − 5𝑦 = 31
В2. Постройте график функции 𝑦 = −2𝑥 + 5. Пользуясь
графиком, найдите:
1) Значение функции, если значение аргумента равно 2;
2) Значение аргумента, если значение функции равно -1.
В3. В прямоугольном треугольнике 𝐴𝐵𝐶 угол между
биссектрисой 𝐶𝐾 и высотой 𝐶𝐻, проведенными из вершины
прямого угла 𝐶, равен 15⁰. 𝐴𝐵 = 14 см.Найдите сторону 𝐴𝐶, если
известно, что точка 𝐾 лежит между 𝐵 и 𝐻.
В1. Решите систему уравнений {