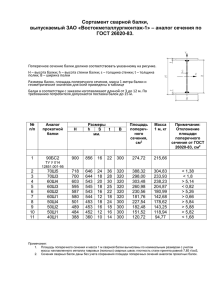
Исходные данные: размеры перекрытия в плане 3А×3В=3·18м×3·6м; отметка верха настила Hн=11.5м; строительная высота перекрытия 2.5 м; характеристическое значение функциональной нагрузки Qk=30кПа; марка стали настила С245 марка стали балки настила С245 марка стали главной балки С345 марка стали колонны С245 Расчет стального настила (на настоящий момент для собственного веса стальных конструкций гамма = 1.2, для функциональной нагрузки гамма Q = 1.4). Принимаем настил из стальных листов толщиной td = 13 мм. Пролёт настила определяем по формуле ld где n0 4 n0 72 E (1 4 1 ) td , 15 n0 Qk ld ; в соответствии с таблицей 49 [1] n0 =250; fu E1 – цилиндрический модуль упругости стали, определяемый по формуле E1 ld E 206000 226374 МПа; 1 2 1 0.32 4 250 72 226374 (1 ) 13 987 мм 15 2504 30 103 Принимаем ld =1000 мм. Расчет настила выполняем как упругой висячей конструкции с учётом напряжений от изгиба и растягивающих напряжений от распора (50 < ld / td = 1000 / 13 = 76.9 < 300). В расчёте рассматриваем участок настила шириной bd = 1 м. В расчётной схеме настил представляет собой стержневой элемент расчетной длиной ld, имеющий по концам шарнирно неподвижные опоры (балки настила) и загруженный равномерно распределенной по его длине нагрузкой. Расчетная схема настила приведена на рисунке 1. q ld Рисунок 1 – Расчётная схема настила Геометрические характеристики рассчитываемого элемента настила: – площадь поперечного сечения Ad = bd·td = 1000·13 = 13000 мм2; – момент сопротивления поперечного сечения Wd , x bd td 2 1000 132 28167 мм3 ; 6 6 – момент инерции поперечного сечения Id ,x bd td 3 1000 133 183083 мм4 . 12 12 Расчетные сочетания нагрузок на рассчитываемый элемент настила: – 1-е основное сочетание q1 k FI G td bd k FI Q 0 Qk bd 11.35 78.5 0.013 1 11.5 0.8 30 1 37.38кН / м – 2-е основное сочетание q2 k FI G td bd k FI Q Qk bd 1 0.85 1.35 78.5 0.013 1 11.5 30 1 46.17 кН / м – сочетание характеристических значений постоянных нагрузок и практически постоянных значений переменных нагрузок qn td bd 2 Qk bd 78.5 0.013 1 0.6 30 1 19.02кН / м , где ρ=78.5 кН/м3 – объёмный вес стали; kFI=1 – коэффициент, применяемый к воздействиям для дифференциации надежности; γG=1.35 и γQ=1.5 – частные коэффициенты безопасности соответственно для постоянного и переменного воздействий; (в соответствии с СН 2.01.012022, таблица А.3 частные коэффициенты безопасности для расчета стальных конструкций принимаются: для нагрузки от собственного веса γG=1.2, для функциональной нагрузки γQ=1.4); ξ=0.85 – понижающий коэффициент; 0=0.8 – коэффициент, учитывающий комбинационное значение переменного воздействия (значение коэффициента принято в соответствии с заданием); -2- 2=0.6 – коэффициент, учитывающий практически постоянное значение переменного воздействия (значение коэффициента принято в соответствии с заданием). Определяем балочный прогиб настила 5 qn ld 4 5 19.02 14 1012 f0 5.98 мм 384 E1 I d , x 384 226374 183083 Определяем коэффициент из решения кубического уравнения (1 2 ) 3( f 0 / td ) 2 3 3( f 0 / td ) 2 0 0.51 Прогиб настила с учетом влияния распора f f0 1 1 5.98 3.96 мм 1 1 0.51 Предельно допустимое значение вертикального прогиба настила определяем по таблице 49 [1]. Вертикальный предельный прогиб настила ld 1000 4.00 мм 250 250 f 3.96 мм fu 4.00 мм fu – прогиб настила от действующей нагрузки не превышает предельно допустимое значение вертикального прогиба. Определяем балочный изгибающий момент в настиле q2 ld 2 46.17 12 M0 5.77кНм 8 8 Максимальный изгибающий момент в настиле с учетом влияния распора M Ed M 0 1 1 5.77 3.82кНм 3821192 Н мм 1 1 0.51 Продольная растягивающая сила (распор) в настиле N Ed 2 E1 I d , x ld 2 3.142 226374 183083 0.51 208403Н 10002 Выполняем проверку прочности настила при действии продольной растягивающей силы и изгибающего момента по формуле N Ed M Ed Ad Wd , x f yd c 1, -3- где fyd=230 МПа – расчётное значение предела текучести стали настила, определённое по таблице А.3 [1]; γc=1 – коэффициент условий работы конструкций и элементов, определённый по таблице Б.1 [1]. 208403 3821192 13000 28167 0.66 1 230 1 – прочность настила обеспечена. Продольную силу, действующую в сварном шве, прикрепляющем настил к балке настила, определяем по приближенной формуле N Ed , w Q 2 f 2 2 3.142 3.96 E1td 1.5 226374 13 170.63Н / мм 4 ld 4 1000 Настил приварен к балкам механизированной сваркой в нижнем положении проволокой СВ-08А. Характеристики для расчета сварного соединения: – характеристическое значение предела прочности стали настила fuk=370 МПа; – расчетное значение прочности углового шва на срез (условный) по металлу шва fwf=180 МПа; – расчетное значение прочности углового шва на срез (условный) по металлу границы сплавления fwz=0.45· fuk =0.45·370=166.5 МПа; – коэффициенты βf=0.9, βz=1.05; – коэффициент условий работы конструкций и элементов γc=1. Так как f f wf 0.9 180 0.93 1, z f wz 1.05 166.5 расчет сварного соединения с угловыми швами выполняем на срез (условный) по металлу шва. Требуемое значение катета шва из условия прочности сварного соединения kf N Ed , w f f wf c 170.63 1.05 мм 0.9 180 1 Минимальное значение катета шва, определенное по таблице 39 [1], k f ,min 4 мм . Сварные швы, прикрепляющие настил к балке настила, выполняем с катетом шва kf = 4 мм. -4- Расчет балки настила В расчёте рассматриваем среднюю балку настила. В расчётной схеме балка настила представляет собой стержневой элемент расчетной длиной lef, имеющий по концам шарнирно подвижную и шарнирно неподвижную опоры (главные балки) и загруженный равномерно распределенной по его длине нагрузкой. Расчетная схема балки настила приведена на рисунке 2. q lef Рисунок 2 – Расчётная схема балки настила Расчетные сочетания нагрузок на 1 м длины балки настила с учетом ее собственного веса, принятого равным 2% от соответствующего сочетания нагрузок: – 1-е основное сочетание q1 k FI G td ld k FI Q 0 Qk ld 1.02 (11.35 78.5 0.013 1 11.5 0.8 30 1) 1.02 38.13кН / м – 2-е основное сочетание q2 k FI G td ld k FI Q Qk ld 1.02 (1 0.85 1.35 78.5 0.013 1 11.5 30 1) 1.02 47.09кН / м Максимальный изгибающий момент в балке настила от 2-го основного сочетания нагрузок равен M Ed q2 lef 2 8 47.09 62 211.91кНм 211.91106 Н мм 8 Требуемое значение момента сопротивления поперечного сечения балки настила из условия прочности балки при действии изгибающего момента с учетом развития пластических деформаций Wx ,треб . M Ed 211.91 106 802689 мм3 802.7см3 , cx f yd c 1.1 240 1 где cx и β – коэффициенты, произведение которых при подборе сечения принято равным 1.1; fyd – расчётное значение предела текучести стали балки настила, определённое по таблице А.5 [1]. -5- Балку настила выполняем из двутавра №40 по ГОСТ 8239-89. Геометрические характеристики балки настила: – высота h = 400 мм; – ширина полки bf = 155 мм; – толщина стенки tw = 8.3 мм; – толщина полки tf = 13 мм; – момент сопротивления поперечного сечения Wx=953 см3; – момент инерции поперечного сечения Ix=19062 см4. Расчетное сочетание нагрузок на 1 м длины балки настила с учетом ее собственного веса (2-е основное сочетание) q2 k FI G td ld k FI G p k FI Q Qk ld 1 0.85 1.35 78.5 0.013 1 1 0.85 1.35 0.57 11.5 30 1 46.83кН / м, где p = 57 кг/м ≈ 0.57 кН/м – нагрузка от собственного веса балки настила согласно ГОСТ 8239-89. Максимальный изгибающий момент в балке настила от 2-го основного сочетания нагрузок равен M Ed q2 lef 2 8 46.83 62 210.74кНм 210.74 106 Н мм 8 Максимальная поперечная сила в балке настила от 2-го основного сочетания нагрузок равна VEd q2 lef 2 46.83 6 140.49кН 140.49 103 Н 2 Касательные напряжения VEd 140.49 103 x 45.26МПа, Aw 3104 где Aw=(h-2·tf)·tw=(400-2·13)·8.3=3104 мм2. Проверяем условие x VEd 0.9 f s , Aw где fs – расчетное значение прочности стали на сдвиг; определяется по формуле, приведённой в таблице 2 [1]; f s 0.58 f yk m 0.58 245 138.6 МПа, 1.025 где fyk – характеристическое значение предела текучести стали балки настила, определённое по таблице А.5 [1]; γm – частный коэффициент по материалу, определённый по таблице 3 [1]. -6- x 45.26МПа 0.9 f s 0.9 138.6 124.7МПа – условие выполняется. Расчет балки настила на прочность при действии изгибающего момента выполняем по формуле (49) [1]. Определяем коэффициенты cx ([1], приложение Е, таблица Е.1) и β (формула (51) [1]). При Af Aw bf t f (h 2t f ) tw 155 13 0.65 (400 2 13) 8.3 для типа сечения 1 cx=1.105. Тогда cxm=0.5·(1+cx)=0.5·(1+1.105)=1.053. В зоне чистого изгиба β=1. Проверяем прочность балки настила: – в зоне чистого изгиба M Ed 210.74 106 0.88 1; cx Wx f yd c 1.053 1 953 103 240 1 – в опорном сечении VEd 140.49 103 0.33 1. Aw f s c (400 2 13) 8.3 138.6 1 Прочность балки при действии изгибающего момента и при действии поперечной силы обеспечена. Сочетание характеристических значений постоянных нагрузок и практически постоянных значений переменных нагрузок на 1 м длины балки настила qn td ld p 2 Qk ld 78.5 0.013 1 0.57 0.6 30 1 19.59кН / м . Определяем прогиб балки настила 4 5 qn lef 5 19.59 64 1012 f 8.4 мм 384 E I x 384 206000 19062 10 4 Вертикальный предельный прогиб балки настила (таблица 49 [1]) lef 6000 24.0 мм 250 250 f 8.4 мм fu 24.0 мм fu – прогиб балки настила от действующей нагрузки не превышает предельно допустимое значение вертикального прогиба. -7- Расчет и конструирование главной балки Главную балку проектируем составного сварного двутаврового сечения из трёх листов: вертикального – стенки и двух горизонтальных – полок. Сварное соединение стенки с полками выполняем автоматической сваркой в заводских условиях. В расчёте рассматриваем главную балку по средней оси. В расчётной схеме главная балка представляет собой стержневой элемент расчетной длиной lef, имеющий по концам шарнирно подвижную и шарнирно неподвижную опоры (колонны) и загруженный равномерно распределенной по его длине нагрузкой. Расчетная схема главной балки приведена на рисунке 3. q lef Рисунок 3 – Расчётная схема главной балки Расчетные сочетания нагрузок на 1 м длины главной балки с учетом ее собственного веса, принятого равным 2% от соответствующего сочетания нагрузок: – 1-е основное сочетание q1 k FI G td B k FI G p B / ld k FI Q 0 Qk B 1.02 (11.35 78.5 0.013 6 1 1.35 0.57 6 /1 1 1.5 0.8 30 6) 1.02 233.46кН / м – 2-е основное сочетание q2 kFI G td B k FI G p B / ld k FI Q Qk B 1.02 (1 0.85 1.35 78.5 0.013 6 1 0.85 1.35 0.57 6 /1 1 1.5 30 6) 1.02 286.57кН / м Максимальный изгибающий момент в главной балке от 2-го основного сочетания нагрузок равен M Ed q2 lef 2 8 286.57 182 11606.09кНм 11606.09 106 Н мм 8 Максимальная поперечная сила в опорном сечении главной балки от 2-го основного сочетания нагрузок равна VEd q2 lef 2 286.57 18 2579.13кН 2579.13 103 Н 2 -8- Требуемое значение момента сопротивления поперечного сечения главной балки из условия прочности балки при действии изгибающего момента без учета развития пластических деформаций Wx ,треб . M Ed 11606.09 106 38686967 мм3 , f yd c 300 1 где fyd – расчётное значение предела текучести стали главной балки, определённое по таблице А.3 [1]. Определяем высоту главной балки из следующих условий. 1. Из условия наименьшего расхода материала (hопт). Принимаем толщину стенки балки tw=14 мм. Оптимальная высота балки hопт k Wx ,треб . tw 1.15 38686967 1912 мм, 14 где k – коэффициент, принимаемый для сварных балок равным 1.2…1.15. 2. Из условия жесткости балки (hmin). Сочетание характеристических значений постоянных нагрузок и практически постоянных значений переменных нагрузок на 1 м длины главной балки qn ( td B p B / ld 2 Qk B) 1.02 (78.5 0.013 6 0.57 6 /1 0.6 30 6) 1.02 119.89кН / м hmin 5 f yd lef lef qn 5 300 18000 250 119.89 571мм, 24 E fu q 24 206000 286.57 где q принимаем равным максимальному значению из q1 и q2. 3. Из максимально возможной заданной высоты (hстр,б). hстр,б hстр,перекр hбалки td 2500 400 13 2087 мм настила Принимаем высоту главной балки h=1950 мм, толщину поясов балки tf=25 мм. Высота стенки балки hw h 2t f 1950 2 25 1900 мм Площадь стенки балки Aw hw tw 1900 14 26600 мм 2 Проверяем прочность балки в опорном сечении VEd 2579130 0.56 1, Aw f s c 26600 172 1 -9- где fs – расчетное значение прочности стали на сдвиг; определяется по формуле, приведённой в таблице 2 [1]; f s 0.58 f yk m 0.58 305 172 МПа, 1.025 где fyk – характеристическое значение предела текучести стали балки настила, определённое по таблице А.3 [1]; γm – частный коэффициент по материалу, определённый по таблице 3 [1]. Прочность балки в опорном сечении при действии поперечной силы обеспечена. Определяем необходимость установки продольных ребер жесткости из условия w 5.5 (п. 8.5.11 [1]) . Условная гибкость стенки w hef tw f yd E 1900 300 5.18 5.5, 14 206000 где hef – расчетная высота стенки балки при проверке устойчивости стенки; для сварных балок hef = hw. Согласно п. 8.5.11 [1] установка продольных ребер не требуется. Ширину поясных листов определяем исходя из обеспечения прочности балки. Требуемый момент инерции поперечного сечения главной балки I x ,треб . Wx ,треб . h 1950 38686967 37 719 792 825 мм 4 2 2 Момент инерции стенки балки tw hw3 14 19003 Iw 8 002 166 667 мм 4 12 12 Требуемый момент инерции поясных листов I f ,треб. I x,треб. I w 37719792825 8002166667 29 717 626 158 мм4 При определении геометрических размеров поясных листов моментом инерции поясов относительно их собственной оси ввиду его малости пренебрегаем. Тогда момент инерции поясных листов относительно нейтральной оси балки определяется формулой 2 hef I f 2 Af , 2 где Af – площадь сечения пояса; hef = h–tf = 1950–25 = 1925 мм – расстояние между центрами тяжести поясных листов. Требуемая площадь сечения пояса балки - 10 - Af ,треб . 2 I f ,треб . hef 2 2 29717626158 16039 мм 2 2 1925 Требуемая ширина пояса балки b f ,треб . Af ,треб . tf 16039 642 мм 25 Принимаем bf=650 мм. При этом соотношение bf h 650 1 1950 3 находится в рекомендуемых пределах bf 1 1 ... . h 3 5 Геометрические характеристики главной балки: – высота h = 1950 мм; – высота стенки hw = 1900 мм; – толщина стенки tw = 14 мм; – ширина полки bf = 650 мм; – толщина полки tf = 25 мм; – площадь поперечного сечения A hw tw 2 bf t f 1900 14 2 650 25 59100 мм2 ; – момент инерции поперечного сечения bf t f 3 tw hw3 Ix 2 bf t f 12 12 2 h tf 2 2 2 650 253 14 19003 1950 25 2 650 25 38 112 062 500 мм 4 ; 12 2 2 12 – момент сопротивления поперечного сечения Wx Ix 38112062500 39 089 295 мм3 ; 0.5 h 0.5 1950 – статический момент полусечения h tf 1950 25 S b f t f tw hw2 / 8 650 25 14 19002 / 8 2 2 2 2 21 958 125 мм3 ; – статический момент пояса h tf 1950 25 S f b f t f 650 25 15 640 625 мм3 . 2 2 2 2 - 11 - Расчетное сочетание нагрузок на 1 м длины главной балки с учетом ее собственного веса (2-е основное сочетание) q2 k FI G td B k FI G p B / ld k FI G A k FI Q Qk B 1 0.85 1.35 78.5 0.013 6 1 0.85 1.35 0.57 6 /1 1 0.85 1.35 78.5 59100 106 11.5 30 6 286.27кН / м Максимальный изгибающий момент в главной балке от 2-го основного сочетания нагрузок равен M Ed q2 lef 2 286.27 182 11593.94кНм 11593.94 106 Н мм 8 8 Максимальная поперечная сила в опорном сечении главной балки от 2-го основного сочетания нагрузок равна VEd q2 lef 2 286.27 18 2576.43кН 2576.43 103 Н 2 Проверяем прочность главной балки: – при действии изгибающего момента M Ed 11593.94 106 0.99 1; Wx f yd c 39089295 300 1 – при действии поперечной силы VEd S 2576430 21958125 0.62 1; I x tw f s c 38112062500 14 172 1 – при одновременном действии в стенке балки момента и поперечной силы: при наличии местного напряжения (на расстоянии 7.5 м от опоры) 0.87 x2 x y y2 3 xy2 f yd c 0.87 280.97 2 280.97 100.34 100.342 3 12.59 2 0.72 1, 300 1 при отсутствии местного напряжения (на расстоянии 8.5 м от опоры) 0.87 0.87 x2 3 xy2 288.12 3 4.22 0.84 1, f yd c 300 1 где σx – нормальное напряжение в срединной плоскости стенки, действующее параллельно продольной оси балки; x M Ed ,1 y Ix M Ed ,1 0.5 hw Ix 11558.15 106 0.5 1900 288.1МПа; 38112062500 - 12 - σy – нормальное напряжение в срединной плоскости стенки, действующее перпендикулярно продольной оси балки; σy = σloc; τxy – касательное напряжение в стенке; xy VEd ,1 S f I x tw 143135 15640625 4.2МПа; 38112062500 14 здесь MEd,1 и VEd,1 – изгибающий момент и поперечная сила в расчетном сечении на уровне поясного шва. Прочность балки при действии изгибающего момента, при действии поперечной силы и при их совместном действии обеспечена. Местное напряжение в стенке главной балки под балкой настила loc FEd 280950 100.34МПа, lef tw 200 14 где FEd – расчетное значение сосредоточенной силы; FEd=46.825·6=280.95кН; lef – условная длина распределения нагрузки; lef = b+2·h=130+2·35=200 мм, здесь b – ширина опирания балки настила; b=10·tf(балки настила) =10·13=130 мм<bf(балки настила)=155 мм; h – размер, равный сумме толщины верхнего пояса главной балки и катета поясного шва; h=25+10=35 мм. Проверяем прочность стенки главной балки под балкой настила при отсутствии ребер жесткости loc 100.34 0.33 1. f yd c 300 1 Прочность стенки балки при действии местного напряжения обеспечена. Условная гибкость сжатого пояса балки при расчете на общую устойчивость b lef bf f yd E 1000 300 0.059, 650 206000 где lef – расчетная длина балки при расчете на общую устойчивость, равная шагу балок настила. Предельная условная гибкость сжатого пояса балки 0.02 b f b f 0.76 tf t h t f f 0.0032 650 0.02 650 650 0.35 0.76 0.514. 25 25 1950 25 ub 0.35 0.0032 b f b 0.059 ub 0.514 - 13 - – общая устойчивость главной балки обеспечена. Проверка на местную устойчивость пояса и стенки главной балки Проверяем устойчивость сжатого пояса. Условная гибкость свеса пояса f bef tf f yd E 318 300 0.485, 25 206000 где bef – свес пояса; bef = (bf–tw)/2 = (650–14)/2 = 318 мм. Предельная условная гибкость свеса пояса f yd uf 0.5 c 0.5 300 0.5, 296.6 где σc – напряжение в сжатом поясе; M Ed 11593.94 106 c 296.6МПа. Wx c 39089295 1 f 0.485 uf 0.5 – устойчивость сжатого пояса главной балки обеспечена. Проверяем устойчивость стенки. Условная гибкость стенки w hef tw f yd E 1900 300 5.18, 14 206000 где hef – расчетная высота стенки; hef = hw. Устанавливаем необходимость укрепления стенки поперечными ребрами жесткости согласно п. 8.5.9 [1]. w 5.18 3.2 – установка поперечных ребер жесткости необходима. Ширина выступающей части поперечного ребра жесткости br hw 1900 25 мм 25 мм 88.3 мм. 30 30 Принимаем br=100 мм. Толщина поперечного ребра жесткости tr 2br f yd E 2 100 320 7.9 мм. 206000 Принимаем tr=8 мм. Расстояние между поперечными ребрами жесткости не должно превышать 3hef=3·1900=5700 мм. Поперечные ребра жесткости устанавливаем в местах приложения сосредоточенных нагрузок (под балками настила). Схема расположения поперечных ребер жесткости приведена на рисунке 4. - 14 - Проверяем выполнение условия п. 8.5.1 [1] w uw . w 5.18 uw 2.5 – условие не выполняется, следовательно, требуется проверка устойчивости стенки, укрепленной поперечными ребрами жесткости. Определяем напряжения в стенке балки в соответствии с п. 8.5.2 [1]. Выполняем расчет для третьего от опоры отсека. Так как длина отсека (расстояние между поперечными ребрами жесткости) a=3 м больше его расчетной высоты hef=1.9 м, то значения Mx,Ed и VEd вычисляем как средние для более напряженного участка длиной, равной hef (на расстоянии 7.55 м от опоры). Mx,Ed = 11293 кН·м, VEd = 415.1 кН. Наибольшее сжимающее напряжение на уровне поясного шва M x , Ed y Ix M x , Ed 0.5 hw Ix 11293 106 0.5 1900 281.49МПа. 38112062500 Среднее касательное напряжение VEd 415.1103 15.61МПа. tw hw 14 1900 Местное напряжение в стенке под балкой настила σloc=100.34 МПа. Проверяем устойчивость стенки в соответствии с п. 8.5.3 [1]. Условная гибкость стенки f yd w 5.18 6 6 300 6.19. 281.49 Так как a/hef = 3/1.9=1.58>0.8, проверку устойчивости стенки выполняем дважды (п. 8.5.5 [1]). 1. Определяем критические напряжения. cr ccr f yd 2 w 32.5 300 363.37 МПа, 5.182 где ccr – коэффициент, определяемый по таблице 13 [1] в зависимости от вида поясных соединений и значения коэффициента , вычисляемого по формуле 3 3 bf t f 650 25 0.8 1.56, hef tw 1900 14 здесь β – коэффициент, определяемый по таблице 14 [1]. loc,cr c1c2 f yd w2 39.02 1.6 300 698.02МПа, 5.182 - 15 - где c1 – коэффициент, определяемый по таблице 15 [1] в зависимости от отношения a1/hef=0.67 (здесь a1=0.67hef при a/hef=1.58>1.33) и значения ρ=1.04lef/hef=1.04·200/1900=0.11; c2 – коэффициент, определяемый по таблице 16 [1] в зависимости от a1/hef=0.67 и =1.56. cr 10.3 1 0.76 f s 0.76 172 2 10.3 1 86.13МПа, 2 2 2 d 1.58 5.18 где μ – отношение большей стороны отсека стенки к меньшей стороне; μ=a/hef=3/1.9=1.58; d d tw f yd E 1900 300 5.18, 14 206000 здесь d – меньшая из сторон отсека стенки (hef или a); d=hef. Проверяем устойчивость стенки балки loc cr loc ,cr 2 cr 2 c 2 2 281.49 100.34 15.61 363.37 698.02 86.13 0.94 1. 1 2. Определяем критические напряжения. cr ccr f yd w2 61.08 300 682.91МПа, 5.182 где ccr – коэффициент, определяемый по таблице 17 [1] в зависимости от отношения a/hef=1.58. loc ,cr c1c2 f yd w2 18.52 1.72 300 356.15МПа, 5.182 где c1 – коэффициент, определяемый по таблице 15 [1] в зависимости от отношения a/hef=1.58 и значения ρ=1.04lef/hef=0.11; c2 – коэффициент, определяемый по таблице 16 [1] в зависимости от a/hef=1.58 и =1.56. Проверяем устойчивость стенки балки loc cr loc ,cr c 2 cr 2 2 2 281.49 100.34 15.61 682.91 356.15 86.13 0.72 1. 1 Выполняем расчет для первого от опоры отсека. Так как длина отсека (расстояние между поперечными ребрами жесткости) a=2.5 м больше его расчетной высоты hef=1.9 м, то значения Mx,Ed и VEd вычисляем как средние для - 16 - более напряженного участка длиной, равной hef (на расстоянии 0.95 м от опоры). Mx,Ed = 2318.43 кН·м, VEd = 2304.47 кН. Наибольшее сжимающее напряжение на уровне поясного шва M x , Ed y Ix M x , Ed 0.5 hw Ix 2318.43 106 0.5 1900 57.79МПа. 38112062500 Среднее касательное напряжение VEd 2304.47 103 86.63МПа. tw hw 14 1900 Местное напряжение в стенке под балкой настила σloc=100.34 МПа. Проверяем устойчивость стенки в соответствии с п. 8.5.3 [1]. Условная гибкость стенки f yd w 5.18 6 6 300 13.67. 57.79 Так как a/hef = 2.5/1.9=1.32>0.8, проверку устойчивости стенки выполняем дважды (п. 8.5.5 [1]). 1. Определяем критические напряжения. cr ccr f yd w2 32.5 300 363.37 МПа, 5.182 где ccr – коэффициент, определяемый по таблице 13 [1] в зависимости от вида поясных соединений и значения коэффициента , вычисляемого по формуле 3 3 bf t f 650 25 0.8 1.56, hef tw 1900 14 здесь β – коэффициент, определяемый по таблице 14 [1]. loc,cr c1c2 f yd 2 w 39.67 1.6 300 709.65МПа, 5.182 где c1 – коэффициент, определяемый по таблице 15 [1] в зависимости от отношения a1/hef=1.25/1.9=0.66 (здесь a1=0.5a при 0.8<a/hef=1.32<1.33) и значения ρ=1.04lef/hef=1.04·200/1900=0.11; c2 – коэффициент, определяемый по таблице 16 [1] в зависимости от a1/hef=0.66 и =1.56. cr 10.3 1 0.76 f s 0.76 172 10.3 1 94.82МПа, 2 2 2 d2 1.32 5.18 где μ – отношение большей стороны отсека стенки к меньшей стороне; μ=a/hef=2.5/1.9=1.32; - 17 - d d tw f yd E 1900 300 5.18, 14 206000 здесь d – меньшая из сторон отсека стенки (hef или a); d=hef. Проверяем устойчивость стенки балки loc cr loc ,cr 2 cr 2 c 2 2 57.79 100.34 86.63 363.37 709.65 94.82 0.96 1. 1 2. Определяем критические напряжения. cr ccr f yd 2 w 49.76 300 556.34МПа, 5.182 где ccr – коэффициент, определяемый по таблице 17 [1] в зависимости от отношения a/hef=1.32. loc ,cr c1c2 f yd 2 w 21.3 1.71 300 407.23МПа, 5.182 где c1 – коэффициент, определяемый по таблице 15 [1] в зависимости от отношения a/hef=1.32 и значения ρ=1.04lef/hef=0.11; c2 – коэффициент, определяемый по таблице 16 [1] в зависимости от a/hef=1.32 и =1.56. Проверяем устойчивость стенки балки loc cr loc ,cr c 2 cr 2 2 2 57.79 100.34 86.63 556.34 407.23 94.82 0.98 1. 1 Устойчивость стенки главной балки обеспечена. Поперечное ребро жесткости проверяем на устойчивость как центрально сжатый элемент на действие сосредоточенной силы FEd=280.95кН. При этом в расчетное сечение стойки включаем сечение ребер жесткости и полосы стенки шириной 0.65tw E / f yd 0.65 14 206000 / 300 238 мм с каждой стороны ребра, а расчетную длину стойки принимаем равной расчетной высоте стенки hef=1900 мм. Площадь расчетного сечения стойки - 18 - A 2 br tr 2 0.65tw E tr t w f yd 206000 2 100 8 2 0.65 14 8 14 8389 мм 2 300 Момент инерции стойки 2 tr br 3 br tw Iz 2 tr br 2 0.65tw 12 2 2 t 3 E tr w 12 f yd 2 8 1003 143 206000 100 14 2 8 100 2 0.65 14 8 12 2 2 300 12 6642618 мм 2 Радиус инерции стойки Iz 6642618 28 мм A 8389 iz Условная гибкость стойки f yd E hef iz f yd E 1900 300 2.6 28 206000 Тип сечения b (таблица 7 [1]). Значение коэффициента устойчивости при центральном сжатии определяем по таблице Д.1 [1]: φ=0.723. Проверяем устойчивость стойки FEd 280950 0.15 1. A f yd c 0.723 8389 300 1 Устойчивость поперечного ребра жесткости обеспечена. Расчет опорного ребра главной балки Требуемая площадь поперечного сечения опорного ребра из расчета прочности на смятие Ar ,треб. N Ed 2576430 5619.3мм2 , f p c 458.5 1 где NEd – опорная реакция главной балки; fp – расчетное значение прочности стали на смятие торцевой поверхности; fp f uk m 470 458.5МПа. 1.025 - 19 - Принимаем ребро толщиной tr=16 мм, шириной br=550 мм. Площадь поперечного сечения опорного ребра Ar=br·tr=550·16=8800мм2 > 2 Ar,треб.=5619.3мм . Высота выступающей за нижний пояс балки части ребра a=15мм<1.5·tr=24мм. Участок стенки балки над опорой проверяем на устойчивость при центральном сжатии из плоскости балки как стойку, нагруженную опорной реакцией NEd=2576.43кН. При ширине выступающей части опорного ребра br≥0.5bfi, где bfi – ширина нижнего пояса балки, (br=550мм>0.5bfi= 0.5·650=325мм), в расчетное сечение стойки включаем сечение опорного ребра жесткости и полосы стенки шириной 0.65tw E / f yd 0.65 14 206000 / 300 238 мм , а расчетную длину стойки принимаем равной расчетной высоте стенки hef=1900 мм. Площадь расчетного сечения стойки A br tr 0.65tw E 206000 tw 550 16 0.65 14 14 12138 мм 2 f yd 300 Момент инерции стойки tr br 3 Iz 0.65tw 12 E t w3 f yd 12 16 5503 206000 143 0.65 14 221887861мм 2 12 300 12 Радиус инерции стойки Iz 221887861 135 мм A 12138 iz Условная гибкость стойки f yd E hef iz f yd E 1900 300 0.54 135 206000 Тип сечения b (таблица 7 [1]). Значение коэффициента устойчивости при центральном сжатии определяем по таблице Д.1 [1]: φ=0.99. Проверяем устойчивость стойки N Ed 2576430 0.95 1. A f yd c 0.99 9098 300 1 Устойчивость опорного ребра жесткости обеспечена. Приварку опорного ребра к стенке балки осуществляем двусторонним швом механизированной сваркой проволокой СВ-10ГА. - 20 - Характеристики для расчета сварного соединения: – характеристическое значение предела прочности стали балки fuk=470 МПа; – расчетное значение прочности углового шва на срез (условный) по металлу шва fwf=215 МПа; – расчетное значение прочности углового шва на срез (условный) по металлу границы сплавления fwz=0.45· fuk =0.45·470=211.5 МПа; – коэффициенты βf=0.8, βz=1; – коэффициент условий работы конструкций и элементов γc=1. Так как f f wf 0.8 215 0.81 1, z f wz 1 211.5 расчет сварного соединения с угловыми швами выполняем на срез (условный) по металлу шва. Расчетная длина флангового шва согласно конструктивным требованиям (п. 14.1.7 [1]) lw 85 f k f . Требуемое значение катета шва из условия прочности сварного соединения N Ed 1 f k f 85 f k f 2 f wf c kf N Ed 2576430 10.5 мм. 85 2f 2 f wf c 85 0.82 2 215 1 Минимальное значение катета шва, определенное по таблице 39 [1], k f ,min 5 мм . Максимальное значение катета шва согласно п. 14.1.7 [1] k f ,max 1.2t 1.2 14 16.8 мм , где t – наименьшая из толщин свариваемых элементов. Сварные швы, прикрепляющие опорное ребро к стенке главной балки, выполняем с катетом шва kf = 11 мм. При этом расчетная длина флангового шва lw 85 f k f 85 0.8 11 748 мм hw 10 мм 1900 10 1890 мм. Опорное ребро привариваем к стенке по всей высоте сплошными швами. Расчет поясных швов Приварку поясных листов к стенке балки осуществляем двусторонними швами автоматической сваркой в лодочку проволокой Св-10ГА. Характеристики для расчета сварного соединения: – характеристическое значение предела прочности стали балки fuk=470 МПа; - 21 - – расчетное значение прочности углового шва на срез (условный) по металлу шва fwf=215 МПа; – расчетное значение прочности углового шва на срез (условный) по металлу границы сплавления fwz=0.45· fuk =0.45·470=211.5 МПа; – коэффициенты βf=1.1, βz=1.15; – коэффициент условий работы конструкций и элементов γc=1. Так как f f wf 1.1 215 0.97 1, z f wz 1.15 211.5 расчет сварного соединения с угловыми швами выполняем на срез (условный) по металлу шва. Максимальная сдвигающая сила под первой от опоры балкой настила V S F TEd Ed f Ed I x lef 1724 Н / мм, 2 2 2 2 2433295 15640625 280950 38112062500 200 где FEd и lef – расчетное значение сосредоточенной силы и условная длина распределения нагрузки из расчета на местное напряжение стенки главной балки под балкой настила. Требуемое значение катета шва из условия прочности сварного соединения kf TEd 1724 3.6 мм. 2 f f wf c 2 1.1 215 1 Минимальное значение катета шва, определенное по таблице 39 [1], k f ,min 10 мм . Сварные швы, прикрепляющие поясные листы к стенке главной балки, выполняем с катетом шва kf = 10 мм. Монтажный стык главной балки Монтажный стык выполняем в середине пролета главной балки. Схема стыка приведена на рисунке 4. Стык осуществляем высокопрочными болтами с номинальным диаметром резьбы d=30мм из стали 40Х с газопламенной обработкой поверхностей соединяемых элементов. Расчетное усилие, воспринимаемое каждой плоскостью трения элементов, стянутых одним высокопрочным болтом Qbh fbh Ab,n h 630 561 0.42 132536 Н , 1.12 - 22 - 1-1 1 180 190 280 280 280 280 45 1950 16 190 25 16 1900 1755 1485 1215 945 675 405 135 1880 16 16 25 25 16 45 360 45 16 25 45 9x90=810 900 1 16 90 90 90 16 45 650 45 Рисунок 5 – Схема монтажного стыка главной балки где fbh – расчетное значение прочности на растяжение высокопрочного болта, принимаемое по таблице Г.8 [1]; fbh=630 МПа; Ab,n – площадь сечения болта нетто (по резьбе); Ab,n=5.61 см2=561 мм2 (таблица Г.9 [1]); μ – коэффициент трения, определяемый по таблице 43 [1]; μ=0.42; γh – коэффициент, определяемый по таблице 43 [1]; γh=1.12. Стык поясов. Верхний и нижний пояса балки перекрываем с двух сторон тремя накладками сечением: наружная – 650х16 мм, внутренние – 280х16 мм. Площадь сечения накладок, перекрываемых один пояс, накл 2 2 A =650·16+2·280·16=19360 мм > Af=bf·tf=650·25=16250 мм . Усилие в поясе балки Nf M Ed I f hef I x 11593.94 106 30109895833 4758248 Н , 1925 38112062500 где If – момент инерции поясных листов; - 23 - bf t f 3 I f 2 bf t f 12 2 h tf 2 2 2 650 253 1950 25 2 650 25 30 109 895 833 мм 4 ; 12 2 2 hef – расчетная высота поясов; hef = hw+tf = 1900+25=1925 мм. Количество болтов для прикрепления накладок (п. 14.3.4 [1]) n Nf Qbh b c 4758248 17.95, 132536 2 11 где κ – количество плоскостей трения соединяемых элементов; κ=2; γb – коэффициент условий работы фрикционного соединения, зависящий от количества n болтов, необходимых для восприятия расчетного усилия; при n≥10 γb=1. Принимаем 18 болтов и размещаем в соответствии с таблицей 41 [1]. Стык стенки. Стенку балки перекрываем двумя вертикальными накладками размерами 1880х360х10. Изгибающий момент в стенке балки Mw M Ed I w 11593.94 8002166667 2434.31кНм, Ix 38112062500 где Iw – момент инерции стенки балки; Iw = 8 002 166 667 мм4. Принимаем расстояние между крайними по высоте рядами болтов amax 1880 2 45 1790 мм. Коэффициент стыка Mw 2434.31106 2.57, m amax Qbh b c 2 1790 132536 2 11 где m – число вертикальных рядов болтов на полунакладке. Число рядов болтов по вертикали k=14 при =2.69>2.57 (таблица 7.9 [2]). Окончательно принимаем 14 рядов болтов по вертикали с шагом 135 мм (2.5d=2.5·31=77.5мм<135мм<8d=8·30=240мм – соответствует конструктивным требованиям (таблица 41 [1]); d=31мм – диаметр отверстия для болта). Расстояние от центра крайнего болта до края элемента (1880-13·135)/2=62.5мм, что больше минимально допустимого расстояния 1.3d=1.3·31=50.7мм и не превышает максимально допустимое расстояние 4d=4·31=124мм (таблица 41 [1]). Расстояние между крайними по высоте рядами болтов amax 13 135 1755 мм. Проверяем прочность стыка стенки балки - 24 - N max M w amax 2434.31 1.755 257.6кН Qbh b c m ai2 2 8.29 132.536 2 1 1 265.07 кН , где a 2 i 0.1352 0.4052 0.6752 0.9452 1.2152 1.4852 1.7552 8.29 м2 . Прочность стыка стенки обеспечена. Проверку сечений, ослабленных отверстиями для болтов во фрикционном соединении, выполняют при статических нагрузках при площади сечения нетто Anet 0.85 A по площади сечения брутто А. Нижний растянутый пояс балки ослаблен двумя отверстиями по краю стыка, тогда пояс Anet 25 (650 2 31) 14700 мм 2 0.85 A 0.85 25 650 13813 мм 2 . Проверку нижнего пояса выполняют по площади сечения брутто. Поясные накладки ослаблены по краю стыка четырьмя отверстиями, тогда накл Anet 19360 4 2 16 31 15392 мм 2 0.85 Aнакл 0.85 19360 16456 мм 2 . Проверку накладок выполняют по условной площади Aef 1.18 Anet . Так как накл Aefнакл 1.18 Anet 1.18 15392 18163мм2 Af 16250 мм2 , расчет прочности по ослабленному сечению накладок можно не производить. Проверка балки по прогибам Сочетание характеристических значений постоянных нагрузок и практически постоянных значений переменных нагрузок на 1 м длины главной балки qn td B p B / ld A 2 Qk B 78.5 0.013 6 0.57 6 /1 78.5 59100 10 6 0.6 30 6 122.18кН / м Максимальный прогиб главной балки в середине пролета 4 5 qn lef 5 122.18 184 1012 f 21.3 мм 384 E I x 384 206000 38112062500 Вертикальный предельный прогиб балки (таблица 49 [1]) lef 18000 72.0 мм. 250 250 f 21.3 мм fu 72.0 мм fu – прогиб главной балки от действующей нагрузки не превышает предельно допустимое значение вертикального прогиба. - 25 - Расчет колонны В расчёте рассматриваем среднюю колонну. В расчётной схеме колонна представляет собой стержневой элемент расчетной длиной lef, имеющий по концам шарнирно подвижную (главные балки) и шарнирно неподвижную (фундамент) опоры и загруженный сосредоточенной продольной силой NEd, приложенной по центру тяжести сечения колонны. Расчетная схема колонны приведена на рисунке 5. lef NEd Рисунок 5 – Расчётная схема колонны Расчетная длина колонны при коэффициенте расчетной длины μ=1 (таблица 31 [1]) lef , x, y H н td hб.н. hгл.б. (11.5 0.013 0.4 1.95) 1 9.14 м Продольная сила в колонне от 2-го основного сочетания нагрузок с учетом собственного веса колонны, принятого равным 1% от сочетания нагрузок, равна NEd q2гл.б. lefгл.б. 1.01 286.27 18 1.01 5204.4кН 5204.4 103 Н Колонну проектируем двутаврового сечения, сваренное из трех листов. Задаемся гибкостью =70. Условная гибкость f yd E 70 230 2.34. 206000 Коэффициент устойчивости при центральном сжатии, определенный по таблице Д.1 для типа сечения с, φ=0.683. Требуемое значение площади поперечного сечения колонны Атреб . N Ed 5204.4 103 33130 мм 2 , f yd c 0.683 230 1 - 26 - где fyd – расчётное значение предела текучести стали колонны, определённое по таблице А.3 [1]. Требуемый радиус инерции поперечного сечения колонны iтреб . lef 9140 130.6 мм. 70 Подбираем ширину колонны по таблице 8.1 [2] bтреб . iтреб . k2 130.6 544 мм. 0.24 Принимаем полки сечением 560х20 мм, стенку сечением 600х18 мм. Площадь поперечного сечения колонны А 2 560 20 600 18 33200 мм 2 . Проверяем общую устойчивость колонны. Момент инерции сечения относительно оси y I y 2 20 5603 /12 600 183 /12 585 678 267 мм4. Радиус инерции относительно оси y iy Iy A 585678267 133 мм. 33200 Гибкость y lef iy 9140 69. 133 Условная гибкость f yd E 69 230 2.31. 206000 Коэффициент устойчивости при центральном сжатии, определенный по таблице Д.1 для типа сечения с, φ=0.689. Проверяем общую устойчивость колонны N Ed 5204.4 103 0.99 1. А f yd c 0.689 33200 230 1 Устойчивость колонны обеспечена. Геометрические характеристики колонны: – высота стенки hw = 600 мм; – ширина полки bf = 560 мм; – толщина стенки tw = 18 мм; – толщина полки tf = 20 мм. Проверяем местную устойчивость стенки колонны. Условная гибкость стенки - 27 - w hef tw f yd E 600 230 1.11, 18 206000 где hef – расчетная высота стенки; hef = hw. Предельная условная гибкость стенки колонны (таблица 9 [1]) при 2.31 2 uw 1.20 0.35 1.20 0.35 2.31 2.01. w 1.11 uw 2.01 – устойчивость стенки колонны обеспечена. Устанавливаем необходимость укрепления стенки поперечными ребрами жесткости согласно п. 7.3.3 [1]. w 1.11 2.3 – установка поперечных ребер жесткости не требуется. Из конструктивных соображений устанавливаем три парных поперечных ребра жесткости. Ширина выступающей части поперечного ребра жесткости br hw 600 40 мм 40 мм 60 мм. 30 30 Принимаем br=100 мм. Толщина поперечного ребра жесткости tr 2br f yd E 2 100 230 6.7 мм. 206000 Принимаем tr=8 мм. Проверяем местную устойчивость поясного листа колонны. Условная гибкость свеса пояса f bef tf f yd E 271 230 0.45, 20 206000 где bef – свес пояса; bef = (bf–tw)/2 = (560–18)/2 = 271 мм. Предельная условная гибкость свеса пояса колонны (таблица 10 [1]) uf 0.36 0.1 0.36 0.1 2.31 0.59. f 0.45 uf 0.59 – устойчивость пояса колонны обеспечена. Расчет оголовка колонны Усилие на стержень колонны передается опорными ребрами главных балок через плиту оголовка. Ширина опорного ребра главной балки br=550 мм. Толщину плиты оголовка принимаем равной tпл.ог.=25 мм. - 28 - Толщину ребер оголовка определяем из условия смятия. Требуемая площадь смятия Аp ,тр. N Ed 5204.4 103 14417 мм 2 , f p c 361 1 где fp – расчетное значение прочности стали на смятие торцевой поверхности; fp fuk m 370 361МПа. 1.025 Условная длина распределения нагрузки l p ,ef br 2tпл.ог. 550 2 25 600 мм. Требуемая толщина ребра оголовка t p ,тр. Аp ,тр. l p ,ef 14417 24 мм. 600 Принимаем толщину ребра tp = 25 мм. Приварку ребер оголовка к стенке колонны осуществляем двусторонним швом механизированной сваркой проволокой СВ-08ГА. Задаемся катетом шва kf = 14 мм (k f ,min 10 мм k f 14 мм k f ,max 1.2t 1.2 18 21.6 мм) . Характеристики для расчета сварного соединения: – характеристическое значение предела прочности стали колонны fuk=370 МПа; – расчетное значение прочности углового шва на срез (условный) по металлу шва fwf=200 МПа; – расчетное значение прочности углового шва на срез (условный) по металлу границы сплавления fwz=0.45· fuk =0.45·370=166.5 МПа; – коэффициенты βf=0.7, βz=1; – коэффициент условий работы конструкций и элементов γc=1. Так как f f wf 0.7 200 0.84 1, z f wz 1166.5 расчет сварного соединения с угловыми швами выполняем на срез (условный) по металлу шва. Требуемая длина сварного шва N Ed 5204.4 103 lw 10 мм 10 мм 674 мм f k f 4 f wf c 0.7 14 4 200 1 - 29 - Принимаем lw=680мм. Расчетная длина флангового шва конструктивным требованиям (п. 14.1.7 согласно [1]) lw 680 мм 85 f k f 85 0.7 14 833 мм. Принимаем высоту ребра оголовка hp=700мм > lw=680мм. Определяем толщину стенки колонны в месте приварки ребер оголовка из условия ее работы на срез N Ed 5204.4 103 tw,ог. 27.95 мм, 2 hp f s c 2 700 133 1 где fs – расчетное значение прочности стали на сдвиг; f s 0.58 f yk m 0.58 235 133МПа. 1.025 Так как толщина стенки колонны tw.=18мм < 27.95мм, делаем вставку в стенке колонны в уровне оголовка. Принимаем толщину вставки tw,ог.=28мм. Расчет базы колонны Принимаем бетон фундамента класса С20/25. Предварительно задаемся размерами опорной плиты в плане 800х800 мм, размерами обреза фундамента 1000х1000 мм. Тогда площадь распределения, принимаемая в соответствии с рисунком 8.24, схема ж) [3] составит Ac1 1000 1000 1000000 мм 2 . Площадь смятия Ac 0 800 800 640000 мм 2 . Расчетная прочность бетона на смятие fcud u f cd 1.2 12.5 15.0МПа, где fcd – расчетная прочность бетона на сжатие; fcd fck / c 20 /1.6 12.5МПа, здесь fck – расчетная прочность бетона на сжатие; γc – частный коэффициент по бетону; при расчете элементов на местное сжатие γc=1.6; ωu – коэффициент, учитывающий повышение прочности бетона при местном сжатии; u 1 kc k f c 1 12.5 0.8 0.02 1.2 u ,max 2.5, здесь kc – коэффициент эффективности бокового обжатия, создаваемого окружающим бетоном; принимают равным 12.5; kf – коэффициент; принимают по таблице 8.4 [3]; - 30 - c – коэффициент, учитывающий относительный уровень бокового обжатия, создаваемого окружающим бетоном c f ctm f cm Ac1 2.2 1000000 Ac1 1 1 0.02 0.07 1 Ac 0 28 640000 Ac 0 1000000 0.07 1 0.0175, 640000 здесь fctm – средняя прочность на осевое растяжение бетона; fctm=2.2 МПа; fcm – средняя прочность на осевое сжатие бетона; fcm=28 МПа; ωu,max – предельное значение коэффициента повышения прочности бетона на смятие; принимают по таблице 8.4 [3]. Требуемая площадь опорной плиты базы колонны из условия работы бетона фундамента на смятие Aпл,треб . N Ed 5204.4 103 346960 мм 2 , u f cud 115.0 где u – коэффициент, зависящий от распределения напряжений по площади смятия; при центральном сжатии и значительной жесткости опорной плиты напряжения под плитой в бетоне можно считать равномерно распределенными, тогда u=1. Так как Апл=800·800=640000мм2 > Апл,треб.=346960мм2, принимаем размеры опорной плиты 800х800 мм. Напряжение под опорной плитой (реактивный отпор фундамента) N Ed 5204.4 103 q 8.13Н / мм 2 . Ac1,треб . 640000 Определяем изгибающие моменты, действующие на полосе единичной ширины разных участков опорной плиты (рисунок 7): – для консольного 1 участка плиты M 1 0.5qc 2 0.5 8.13 1042 43967.0 Н мм, – для участка 2, опертого на четыре стороны, в направлении короткой и длинной сторон соответственно M a 1qa 2 0.125 8.13 2712 74634.4 Н мм, M b 2 qa 2 0.037 8.13 2712 22091.8 Н мм, – для участка 3, опертого по трем сторонам, расчет выполняем как для консольного участка, так как a1/d1=80/560=0.14<0.5 M 3 0.5qa12 0.5 8.13 802 26016 Н мм, где с – вылет консольного участка плиты; - 31 - a – короткая сторона участка плиты; d1 – длина свободной стороны участка плиты; a1 – длина стороны, перпендикулярной свободной стороне участка плиты; 1, 2, 3 – коэффициенты, зависящие от условий опирания и отношения размеров сторон участка плиты; принимают по таблице Е.2 [1]. Опорную плиту выполняем из стали С345. Толщина опорной плиты из расчета на изгиб пластинки при действии наибольшего из расчетных изгибающих моментов Mmax,Ed=Ma tпл 6 M max, Ed f yd c 6 74634.4 38.6 мм. 300 1 Принимаем толщину опорной плиты tпл=40 мм. Траверса работает на изгиб как двухконсольная балка, шарнирно опертая на полки колонны. Нагрузка на траверсу – реактивный отпор фундамента с половины ширины опорной плиты qtr q Bпл / 2 8.13 800 / 2 3252 Н / мм. Определяем высоту траверсы из условия размещения сварных швов, необходимых для ее крепления к полкам колонны. Приварку траверсы к полкам колонны осуществляем односторонним швом механизированной сваркой проволокой СВ-08ГА. Задаемся катетом шва kf = 14 мм (k f ,min 10 мм k f 14 мм k f ,max 1.2t 1.2 16 19.2 мм) . Характеристики для расчета сварного соединения: – характеристическое значение предела прочности стали колонны fuk=370 МПа; – расчетное значение прочности углового шва на срез (условный) по металлу шва fwf=200 МПа; - 32 - 16 Bпл=800 3 560 104 a) 2 20 80 16 600 104 80 20 1 Lпл=800 2 б) 1 htr =700 qtr 90 B/ 620 2 90 1 п= Рисунок К расчету колонны Рисунок 7 - 6К –расчету базыбазы колонны: а) конструкция базы; а) конструкция базы; б) расчетная схема траверсы б) расчетная схема траверсы - 33 - – расчетное значение прочности углового шва на срез (условный) по металлу границы сплавления fwz=0.45· fuk =0.45·370=166.5 МПа; – коэффициенты βf=0.7, βz=1; – коэффициент условий работы конструкций и элементов γc=1. Так как f f wf 0.7 200 0.84 1, z f wz 1166.5 расчет сварного соединения с угловыми швами выполняем на срез (условный) по металлу шва. Требуемая длина сварного шва lw qtr Lпл 3252 800 10 мм 10 мм 674 мм 2 f k f f wf c 2 0.7 14 200 1 Принимаем lw=680мм. Расчетная длина флангового шва конструктивным требованиям (п. 14.1.7 согласно [1]) lw 680 мм 85 f k f 85 0.7 14 833 мм. Принимаема высоту траверсы htr=700мм > lw=680мм. Изгибающий момент в середине пролета траверсы (сечение 1-1) qtr ltr 2 qtr ctr 2 3252 6202 3252 902 M Ed ,1 8 2 8 2 143088000 Нмм 143.088кНм. Изгибающий момент в месте приварки траверсы к колонне (сечение 2-2) M Ed ,2 qtr 802 3252 802 10406400 Нмм 10.406кНм. 2 2 Поперечная сила в сечении 2-2 VEd ,2 qtr 80 3252 80 260160 Н 260.16кН . Геометрические характеристики траверсы базы колонны: – высота htr = 700 мм; – толщина ttr = 16 мм; – площадь поперечного сечения Atr htr ttr 700 16 11200 мм 2 ; – момент инерции поперечного сечения ttr htr 3 16 7003 I tr 457333333 мм4 ; 12 12 – момент сопротивления поперечного сечения ttr htr 2 16 7002 Wtr 1306667 мм3 . 6 6 - 34 - Проверка прочности траверсы в сечении 1-1 M Ed ,1 Wtr f yd c 143088000 0.48 1. 1306667 230 1 Проверка прочности траверсы в сечении 2-2 0.87 0.87 x2 3 xy2 7.962 3 23.232 0.16 1, f yd c 230 1 где x M Ed ,2 xy Wtr VEd ,2 Atr 10406400 7.96МПа; 1306667 260160 23.23МПа. 11200 Прочность траверсы при действии изгибающего момента и при совместном действии изгибающего момента и поперечной силы обеспечена. Приварку траверсы к опорной плите осуществляем механизированной сваркой проволокой СВ-10ГА. Характеристики для расчета сварного соединения траверсы с опорной плитой: – характеристическое значение предела прочности стали траверсы fuk=370 МПа; – расчетное значение прочности углового шва на срез (условный) по металлу шва fwf=215 МПа; – расчетное значение прочности углового шва на срез (условный) по металлу границы сплавления fwz=0.45· fuk =0.45·370=166.5 МПа; – коэффициенты βf=0.7, βz=1; – коэффициент условий работы конструкций и элементов γc=1. Так как f f wf 0.7 215 0.9 1, z f wz 1166.5 расчет сварного соединения с угловыми швами выполняем на срез (условный) по металлу шва. Катет швов, прикрепляющих траверсу к опорной плите kf Принимаем qtr Lпл 3252 800 18.6 мм. f lw f wf c 0.7 930 215 1 катет сварного шва kf = 19 мм. При этом k f ,min 10 мм k f 19 мм k f ,max 1.2t 1.2 16 19.2 мм. Анкерные болты принимаем конструктивно диаметром 24 мм, глубина заделки 580 мм. - 35 - СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ 1. СП 5.04.01-2021. Стальные конструкции. – Минск: Минстройархитектуры, 2021. – 147 с. 2. Металлические конструкции: учебник для студ. учреждений высш. проф. образования / [Ю.И. Кудишин, Е.И. Беленя, В.С. Игнатьева и др.] ; под ред. Ю.И. Кудишина. - 13-е изд., испр. - М.: Издательский центр «Академия», 2011. – 688 с. 3. СП 5.03.01-2020. Бетонные и железобетонные конструкции. – Минск: Минстройархитектуры, 2020. – 236 с. - 36 -