otchet po laboratornoe rabote-3

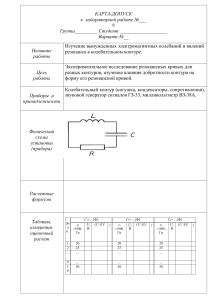
МИНОБРНАУКИ РОССИИ
Государственное образовательное учреждение высшего
профессионального образования
Санкт-Петербургский государственный электротехнический
университет «ЛЭТИ»
Кафедра ТОЭ
Отчет по лабораторной работе №3
«Исследование свободных процессов
в электрических цепях»
Выполнил:
Проверил: преподаватель
Соколов В. Н.
Санкт-Петербург
2016 г.
Цель: изучение связи между видом свободного процесса в электрической цепи и
расположением собственных частот (корней характеристического полинома) на
комплексной плоскости; экспериментальное определение собственных частот и
добротности 𝑅𝐿𝐶-контура по осциллограммам.
Обработка результатов:
1. Исследование свободных процессов в цепи первого порядка.
Исходная цепь: 𝐶 = 0,02 мкФ 𝑅 = 5 кОм
Диаграмма
собственных частот
Найдём собственную частоту:
𝑈1
17,236
𝑝 = − (ln )⁄∆𝑡 = − ln
⁄(62,5 ∙ 10−6 ) = −10482
𝑈2
8,952
1
1
𝑝=−
=−
= −10000
3
𝑅𝐶
5 ∙ 10 ∙ 2 ∙ 10−8
Найденная частота соответствует практической с высокой
точностью.
В общем виде: 𝑈(𝑡) = 𝐴𝑒 −10000𝑡
2. Исследование свободных процессов в цепи второго порядка.
Исходная цепь: 𝑅1 = 0,5 (кОм) (колебательный режим): 𝐶 = 0,02 мкФ
𝐿 = 25 мГн
Найдём собственные частоты:
𝑈1
5,737
𝛼 = (ln )⁄∆𝑡 = (ln
)⁄(147,727 ∙ 10−6 ) = 9655
𝑈2
1,378
𝑝1,2 = −𝛼 ± 𝑗
Диаграмма
собственных частот
2𝜋
2𝜋
= −9655 ± 𝑗
= −9655 ± 𝑗 ∙ 42532
𝑇
147,727 ∙ 10−6
𝛼 = 𝑅⁄2𝐿 = 10000
𝑝1,2 = −𝛼 ± √𝛼 2 − 𝜔02 (
) = −10000 ± 𝑗 ∙ 43589
𝜔0 = 1⁄√𝐿𝐶 = 44721
Найдём добротность
𝑄=
𝜋
𝜋
=
= 2,203;
𝑈
5,737
ln 𝑈1 ln
1,378
2
𝑄=
𝜔0 𝛼 = 𝑅⁄2𝐿 = 10000
(
) = 2,236
2𝛼 𝜔0 = 1⁄√𝐿𝐶 = 44721
В общем виде:
𝑈(𝑡) = 𝐴1 𝑒 −10000𝑡 cos(44721𝑡) + 𝐴2 𝑒 −10000𝑡 sin(44721𝑡)
3. Апериодеский режим: 𝑅1 = 3 (кОм)
Диаграмма
собственных частот
Найдём собственные частоты:
α = R⁄2L = 60000
p1,2 = −α ± √α2 − ω20 (
) = −60000 ± 40000
ω0 = 1⁄√LC = 44721
p1 = −100000
p2 = −20000
В общем виде:
𝑈(𝑡) = 𝐴1 𝑒 −100000𝑡 + 𝐴2 𝑒 −20000𝑡
4. Критический режим: 𝑅1 = 𝑅КР = 2.24 (кОм)
Диаграмма
собственных частот
Найдём собственные частоты, используя схему:
𝛼 = 𝑅 ⁄2𝐿 = 44800
𝑝1,2 = −𝛼 ± √𝛼 2 − 𝜔02 (
) = −44800
𝜔0 = 1⁄√𝐿𝐶 = 44721
𝑝1,2 = −44800
В общем виде: 𝑈(𝑡) = 𝐴1 𝑒 −44800𝑡 + 𝐴2 𝑡𝑒 −44800𝑡
5. Свободный колебательный режим: 𝑅1 = 0 (кОм)
Диаграмма
собственных частот
Найдём собственные частоты:
𝛼 = 𝑅 ⁄2𝐿 = 0
𝑝1,2 = −𝛼 ± √𝛼 2 − 𝜔02 (
) = ±𝑗 ∙ 211
𝜔0 = 1⁄√𝐿𝐶 = 44721
Найдём добротность:
𝜋𝑛
2𝜋
𝑄=
=
= 44
𝑈
23,377
ln 1 ln
𝑈2
20,272
𝑄=
𝜔0
𝛼 = 𝑅 ⁄2𝐿 = 0
(
)=∞
2𝛼 𝜔0 = 1⁄√𝐿𝐶 = 44721
Контур не идеальный, но добротность этого контура в разы выше, чем первого.
В общем виде:
𝑈(𝑡) = 𝐴1 cos(211𝑡) + 𝐴2 sin(211𝑡)
6. Исследование свободных процессов в цепи третьего порядка.
Исходная цепь: 𝐶 = 0,02 мкФ 𝐿 = 25 мГн 𝑅 = 5 кОм 𝑅1 = 1 кОм
Найдём собственные частоты, используя схему:
1
𝑝1 = −
= −10000
𝑅𝐶
2
𝑝2,3
1 𝑅1
1
1 𝑅1
1
2 + 𝑅1 /𝑅
=− ( +
) ± √( ( +
)) −
2 𝐿 𝑅𝐶
2 𝐿 𝑅𝐶
𝐿𝐶
= −25000 ± 𝑗 ∙ 61441
В общем виде: 𝑈(𝑡) = 𝐴1 𝑒 −10000𝑡 + 𝐴2 𝑒 −25000𝑡 cos(61441𝑡) + 𝐴3 𝑒 −25000𝑡 sin(61441𝑡)
Вывод:
Форма реакции цепи зависит от вида собственных частот, если вещественные –
апериодический режим, если комплексно-сопряженные – периодический режим, если
кратные – критический апериодический режим. Результаты аналитических расчетов
не совпадают с данными осцилограмм, так как цепь неидельна.