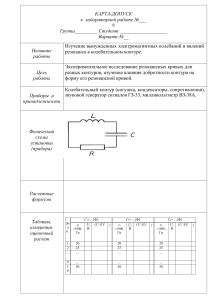
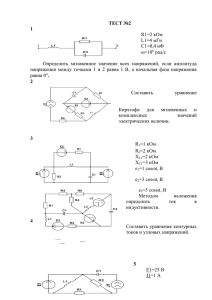
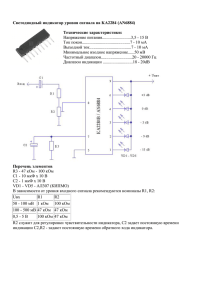
МИНОБРНАУКИ РОССИИ САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ЭЛЕКТРОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ «ЛЭТИ» ИМ. В.И. УЛЬЯНОВА (ЛЕНИНА) Кафедра ТОЭ ОТЧЕТ по лабораторной работе № 3 по дисциплине «Теоретические основы электротехники» ТЕМА: Исследований свободных процессов в электрических цепях Студент гр. 0321 Земсков Д. И. Преподаватель Езеров К. С. г. Санкт-Петербург 2022 Цель работы: изучение связи между видом свободного процесса в цепи и расположением собственных частот (корней характеристического уравнения) на комплексной плоскости; приближенная оценка собственных частот и добротности RLC - контура по осциллограммам. 3.2.1. Исследование свободных процессов в цепи первого порядка Рис. 1 - Схема цепи первого порядка Рис. 2 – осциллограмма напряжения на конденсаторе Полупериод Т = 0,1 мс * 6 = 0,6 мс, f = 1/T = 1/(0,6 мс * 2) = 833 Гц Вопрос 1. Осциллографируемый процесс описывается формулой: 𝑢(𝑡) = 𝐴𝑒 𝑝1𝑡 = 𝐴𝑒 −𝛼𝑡 = 𝐴𝑒 −𝑡/𝜏 Вопрос 2. Собственная частота определяется по осциллограмме, 1 определяется по формуле 𝑝1 = −𝛼 = − , где = 0,1 мс, тогда = -10 000. 𝜏 Что соответствует теоретическому расчету: 1 1 𝛼=− = = −10000 𝑅𝐶 (5 ∗ 103 )Ом ∗ (0,02 ∗ 10−6 )Ф Im . −104 Re Рис. 3 - Расположение частоты на комплексной плоскости 3.2.2. Исследование свободного процесса в цепи второго порядка Рис. 4 - Схема цепи второго порядка Рис. 5 - Осциллограммы напряжения на резисторе при R1 = 0,5 кОм (колебательный режим) Рис. 6 - Осциллограммы напряжения на резисторе при R1 = 3 кОм (апериодический режим) Рис. 7 - Осциллограмма напряжения на резисторе при R1 = R1кр = 2 кОм Рис. 8 - Осциллограмма напряжения на конденсаторе при значениях R1 = 0 Собственные частоты цепи при R1 = 0,5 кОм: 𝑅1 0,5 ∗ 103 1 1 𝛼= = = 10 000, 𝜔 = = 0 2𝐿 2 ∗ 25 ∗ 10−3 √𝐿𝐶 √25 ∗ 10−3 ∗ 0,02 ∗ 10−6 = 44 721 2 𝜔 = √𝜔0 − 𝛼 2 = √(104 )2 − 44 7212 ≈ j*43 589 𝑝1,2 = −𝛼 ± √𝜔02 − 𝛼 2 = −10000 ± 𝑗 ∗ 43 589 Собственные частоты цепи при R1 = R1кр = 2 кОм: 𝑅1 2 ∗ 103 1 1 𝛼= = = 40 000, 𝜔 = = 0 2𝐿 2 ∗ 25 ∗ 10−3 √𝐿𝐶 √25 ∗ 10−3 ∗ 0,02 ∗ 10−6 = 44 721 2 𝜔 = √𝜔0 − 𝛼 2 = √(4 ∗ 104 )2 − 44 7212 ≈ j*20 000 𝑝1,2 = −𝛼 ± √𝜔02 − 𝛼 2 = −40 000 ± 𝑗 ∗ 20 000 Собственные частоты цепи при R1 = 3 кОм: 𝑅1 3 ∗ 103 1 1 𝛼= = = 60 000, 𝜔 = = 0 2𝐿 2 ∗ 25 ∗ 10−3 √𝐿𝐶 √25 ∗ 10−3 ∗ 0,02 ∗ 10−6 = 44 721 2 𝜔 = √𝜔0 − 𝛼 2 = √(6 ∗ 104 )2 − 44 7212 ≈ 40 000 𝑝1,2 = −𝛼 ± √𝜔02 − 𝛼 2 = −60 000 ± 40 000 ⇒ 𝑝1 = −20 000, 𝑝2 = −100 000 Добротность контура при R1 = 0 Ом: 𝐿 0,025 𝑄 = 𝜔0 = ∗ 44 721 → ∞ 𝑅 0 Добротность контура при R1 = 0,5 кОм: 𝐿 0,025 𝑄 = 𝜔0 = ∗ 44 721 = 2,24 𝑅 500 Вопрос 3. Графики процессов описываются выражением: 𝑢(𝑡) = 𝐴1 𝑒 −∝1𝑡 + 𝐴2 𝑒 −∝2𝑡 для апериодического режима (R1 = 3 кОм); 𝑢(𝑡) = 𝐴1 𝑒 −∝𝑡 + 𝐴2 𝑡𝑒 −∝𝑡 , где А1 = 0 для предельного апериодического (критического) режима (R1кр = 2 кОм); 𝑢(𝑡) = 𝐴𝑒 −𝛼𝑡 𝑐𝑜𝑠( 𝜔𝑡 + 𝛽) для колебательного режима (R1 = 0,5 кОм). Вопрос 4. Расчёт частоты цепи при R1 = 0,5 кОм: 4 ∗ 0,1 мс 𝑇= ≈ 0,133 мс 3 периода 𝑢1 = 4 ∗ 0,05 𝐵 = 0,2 В; 𝑢2 = 1,6 ∗ 0,05 = 0,08 𝐵 ln(𝑢1 ⁄𝑢2 ) ln(0.2⁄0.08) 𝛼= = = 6 890, 𝑇 0,133 ∗ 10−3 2𝜋 2∗𝜋 𝜔0 = = = 47 242 𝑇 0,133 ∗ 10−3 𝑝1,2 = −𝛼 ± 𝑗𝜔 = −6 890 ± 𝑗 ∗ 47 242 – практическое значение отличается от значения, полученного при помощи теоретического расчета: −10000 ± 𝑗 ∗ 43 589 Погрешность можно обосновать погрешностью средств измерений и погрешностью номиналов радиодеталей в схеме. . . . −10000 + 𝑗 43589 −10 Im . 4,5 ∗ 104 Re 4 −10000 − 𝑗 43589 Рис. 9 - Расположение частоты на комплексной плоскости Расчёт частоты цепи при R1 = R1кр = 2 кОм: 1 1 𝑝1 = 𝑝2 = −∝= − = − = −100 000 – практическое значение 𝑡𝑚 0.1∗0.1 мс похоже на значение, полученное при помощи теоретического расчета: 𝑝1,2 = −𝛼 ± √𝜔02 − 𝛼 2 = −40 000 ± 𝑗 ∗ 20 000 Погрешность можно обосновать погрешностью средств измерений и погрешностью номиналов радиодеталей в схеме. . . . Im −40000 + 𝑗 20 000 −10 Re 4 −40000 − 𝑗 20 000 Рис. 10 - Расположение частоты на комплексной плоскости Вопрос 5. Расчёт частоты цепи при R1 = 3 кОм: 𝑇 = 2,5 ∗ 0,1 мс ≈ 0,25 мс 𝑢1 = 3 ∗ 0,2 𝐵 = 0,6 В; 𝑢2 = 0,4 ∗ 0,2 𝐵 = 0,08 𝐵 ln(𝑢1 ⁄𝑢2 ) ln(0.6⁄0.08) 𝛼= = = 8 060, 𝑇 0,25 ∗ 10−3 2𝜋 2∗𝜋 𝜔0 = = = 25 133 𝑇 0,25 ∗ 10−3 𝑝1,2 = −𝛼 ± 𝑗𝜔 = −8 060 ± 25 133 ⇒ 𝑝1 = 17 073, 𝑝2 = −33 193 – практическое значение отличается от значения, полученного при помощи теоретического расчета: 𝑝1 = −20 000, 𝑝2 = −100 000 Погрешность можно обосновать погрешностью средств измерений и погрешностью номиналов радиодеталей в схеме. Im . −10 ∗ 104 . . −2 ∗ 104 Re Рис. 11 - Расположение частоты на комплексной плоскости Вопрос 6. Добротность контура при R1 = 0,5 кОм (полученная экспериментально): 𝑛𝜋 4𝜋 𝑄= = 4∗0.05 В = 5.5, (Q > 0.5 соответствует колебательному 𝑢(𝑡) 𝑙𝑛 𝑢(𝑡+𝑛𝑇) 𝑙𝑛 0,4∗0.05 В режиму) Q при теоретическом расчёте = 2,24 Для R1=0: Q→ ∞ 3.2.3. Исследование свободных процессов в цепи третьего порядка Рис. 12 - Схема цепи третьего порядка Рис. 13 - Осциллограмма напряжения для цепи третьего порядка Вопрос 7. Осциллографируемый процесс описывается выражением: 𝑢(𝑡) = 𝑒 −𝛼𝑡 (𝐴1 𝑐𝑜𝑠𝜔𝑡 + 𝐴2 𝑠𝑖𝑛𝜔𝑡) + 𝐴3 𝑒 −𝑝1𝑡 Вопрос 8. С = 0,02 мкФ, R = 5 кОм, R1 = 5 кОм, L = 25 мГн 1 1 𝑝1 = −𝛼1 = − =− = −10 000 𝑅𝐶 5 ∗ 103 ∗ 0,02 ∗ 10−6 1 𝑅1 1 5 ∗ 103 1 𝛼2 = ( + + ) = 0,5 ∗ ( ) = 105 000 2 𝐿 𝑅𝐶 25 ∗ 10−3 5 ∗ 103 ∗ 0,02 ∗ 10−6 √ 𝑝2,3 = −𝛼2 ± 𝛼22 − 𝑅1 𝑅 𝐿𝐶 2+ = −105 000 ± √105 0002 − 2 + 5000/5000 25 ∗ 10−3 ∗ 0,02 ∗ 10−6 = −105 000 ± √11 ∗ 109 − 6 ∗ 109 = (−105 000 ± 𝑗 ∗ 2 236) . . . 104 (−10,5 + 𝑗 ∗ 0,2) −10,5 ∗ 10 4 Im Re 4 10 (−10,5 − 𝑗 ∗ 0,2) Рис. 14 - Расположение частоты на комплексной плоскости Снятая осциллограмма соответствует вычисленным значениям собственных частот. Вывод: в ходе работы было проведено исследование свободных процессов в цепи первого, второго и третьего порядка. Был произведён расчёт собственных частот цепи, а также добротность при помощи теоретического и экспериментального подхода к измерениям. В результате полученных расчётов и измерений теоретические данные совпали с практическими.