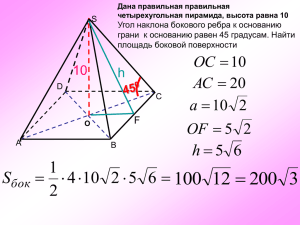
Многогранники Поверхность, составленную из многоугольников и ограничивающую некоторое геометрическое тело, называют многогранной поверхностью или многогранником. Примеры многогранников Тетраэдр Параллелепипед Октаэдр Многоугольники, из которых составлен многогранник, называются его гранями. Например, АА1D1A (перечислите остальные) Стороны граней называются рёбрами (AD, DC, перечислите остальные), а концы рёбер – вершинами (А, В, перечислите остальные) многогранника. Отрезок, соединяющий две вершины , не принадлежащие одной грани, называется диагональю (DB1, перечислите остальные) многогранника. Многогранник называется выпуклым, если он расположен по одну сторону от плоскости каждой его грани. Невыпуклый многогранник Прямые и наклонные многогранники В любом выпуклом многограннике сумма числа граней и числа вершин больше числа рёбер на 2. f + e – k =2 f- число граней; е – число вершин; k – число рёбер. Например, для пирамиды (см. рисунок): f = 5- число граней; e = 5– число вершин; k = 8– число рёбер. Проверка: 5+5-8=2 -верно ПОСТРОЕНИЕ ПРИЗМЫ α β Определение Bn B1 B2 An A1 A2 A3 B3 Многогранник, составленный из двух равных многоугольников A1А2…Аn и B1B2…Bn , расположенных в параллельных плоскостях , и n параллелограммов A1А2В2В1, A2А3В3В2,…,AnА1В1Вn, называется призмой. ВЕРШИНЫ F1 E1 A1 D1 B1 C1 E F D A B C РЕБРА ОСНОВАНИЯ F1 E1 A1 D1 B1 C1 E F D A B C БОКОВЫЕ РЕБРА F1 E1 A1 D1 B1 C1 E F D A B C ГРАНИ ОСНОВАНИЯ F1 E1 A1 D1 B1 C1 E F D A B C БОКОВЫЕ ГРАНИ F1 E1 A1 D1 B1 C1 E F D A B C ВЫСОТА F1 A1 E1 M B1 D1 C1 E F N A B D C ДИАГОНАЛИ F1 E1 A1 D1 B1 C1 E F D A B C ЭЛЕМЕНТЫ ПРИЗМЫ. 1. Вершины 2. Ребра A,B,C,D,E,F,A1,B1,C1,D1,E1,F1 Основания: AB,BC,…,A1D1,B1C1,… Боковые: AA1, DD1, BB1, CC1, EE1, FF1 3. Грани Основания: ABCDEF, A1B1C1D1E1F1 Боковые: AA1B1B, CC1D1D, … 4. Высота 5. Диагональ MN=H – высота призмы Призмы: A1D, AD1, … Боковой грани: A1B, B1C, C1D, … Основания: AD,A1D1, … Площадью полной поверхности призмы называется сумма площадей всех граней (т.е. оснований и боковых граней). Sполн = 2Sосн + Sбок Площадь боковой поверхности призмы равна произведению периметра основания на высоту призмы. Sбок = Ph Виды призм по n -угольнику в основании: D1 C1 A1 A1 B1 F1 A D1 B1 D C1 B A Треугольная B1 E1 A1 C C1 F E B Четырехугольная A D B C C Шестиугольная Правильная призма Правильной называется прямая призма, в основании которой лежит правильный многоугольник. Правильными называют многоугольники, у которых равны все стороны и все углы. Площади полной и боковой поверхностей, объём правильной треугольной призмы. 1. S осн Н 3. а 4. 5. Sполн. a2 3 4 2. Росн.= 3a Sбок Pосн H 3a H a2 3 Sбок 2 Sосн 3 a H 2 4 V S осн a2 3 Н H 4 Площади полной и боковой поверхностей, объём правильной четырехугольной призмы. D1 C1 A1 B1 2 S = a осн 1. Н 3. D A C а B 2. Росн.= 4a Sбок Pосн H 4a H 4. Sполн. Sбок 2 Sосн 4 a H 2 a 2 5. V Sосн Н a 2 H Площади полной и боковой поверхностей, объём правильной шестиугольной призмы. а Н 1. S осн 2. Росн.= 6a 3. 4. Sполн. a2 3 3 a2 3 6 4 2 Sбок Pосн H 6a H 3 a2 3 Sбок 2 Sосн 6 a H 2 6 a H 3 a2 3 2 5. V S осн 3a 2 3 Н H 2 Сечение- это изображение фигуры, полученное при мысленном рассечении Плоскость называется секущей плоскостью многогранника, если по обе стороны этой плоскости имеются точки данного многогранника. Многоугольник, сторонами которого являются отрезки, по которым секущая плоскость пресекает грани многогранника, называется сечением многогранника. Сечения призмы. L M C1 A1 D A C K B N Параллельное боковому ребру C A Перпендикулярное боковому ребру Диагональное Многогранник, составленный из n –угольника и n треугольников, называется пирамидой. реугольная пирамида – Четырехугольная пирамида Шестиугольная пирамид Тетраэдр Площадью полной поверхности пирамиды называется сумма площадей всех граней (т.е. основания и боковых граней). Sполн = Sосн + Sбок Площадью боковой поверхности пирамиды называется сумма площадей её боковых граней. Пирамида называется правильной, если её основание – правильный многоугольник, а отрезок, соединяющий вершину пирамиды с центром основания, является её высотой Площадью боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему Sбок = 𝟏 𝟐 𝑷∙𝒉 P – периметр основания, h = РМ - апофема Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется АПОФЕМОЙ Многогранник, гранями которого являются n – угольники (нижнее и верхнее основания), расположенные в параллельных плоскостях, и n четырёхугольников (боковые грани), называется усечённой пирамидой. Перпендикуляр, проведенный из какой – нибудь точки одного основания к плоскости другого основания, называется высотой усечённой пирамиды Отрезки А1 В1, А2 В2, …..An Bn называются боковыми рёбрами усечённой пирамиды Боковые грани усечённой пирамиды- трапеции Усеченная пирамида называется правильной, если она получена сечением правильной пирамиды плоскостью, параллельной основанию Основания правильной усечённой пирамиды – правильные многоугольники, а боковые грани – равнобедренные трапеции Площадь боковой поверхности правильной усечённой пирамиды равна произведению полусуммы периметров оснований на апофему Sбок = 𝟏 𝟐 ( P 1 + P2 ) h Апофема правильной усечённой пирамиды