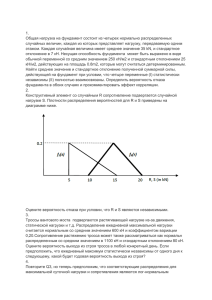
Оценка погрешностей измерений. Расчет выборочного стандартного отклонения Пусть измеряемая имеет известное значение величина X. Естественно, отдельные, найденные в процессе измерения значения этой величины x1, x2,…xn заведомо не вполне точны, т.е. не совпадают с X. Тогда величина будет являться абсолютной погрешностью i-го измерения. Но поскольку истинное значение результата X, как правило, не известно, то реальную оценку абсолютной погрешности используя вместо X среднее арифметическое ,которое рассчитывают по формуле: (1) Однако при малых объемах выборки вместо предпочтительнее пользоваться медианой. Медианой (Ме) называют такое значение случайной величины х, при котором половина результатов имеет значение меньшее, а другая большее, чем Ме. Для вычисления Ме результаты располагают в порядке возрастания, то есть образуют так называемый вариационный ряд. Для нечетного количества измерений n мeдиана равна значению среднего члена ряда. Например, для n=3 Для четных n, значение Ме равно полусумме значений двух средних результатов. Например, для n=4 Далее рассчитывают среднеквадратичную погрешность (стандартное отклонение выборки), являющуюся мерой разброса и характеризующую случайную погрешность определения: (2) Выборочное стандартное отклонение s зависит от объема выборки n и ее значение колеблется по случайному закону около постоянного значения генерального стандартного отклонения σ Для расчета s пользуются неокругленными результатами анализа с неточным последним десятичным знаком. При очень большом числе выборки (n> ) случайные погрешности могут быть описаны при помощи нормального закона распределения Гаусса. При малых n распределение может отличаться от нормального. В математической статистике эта дополнительная ненадежность устраняется модифицированным симметричным t-распределением. Существует некоторый коэффициент t, называемый коэффициентом Стьюдента, который в зависимости от числа степеней свободы (f) и доверительной вероятности (Р) позволяет перейти от выборки к генеральной совокупности. Стандартное отклонение среднего результата определяется по формуле: (3) Разности между средним выборки и средним значением генеральной совокупности μ лежат в Р случаях в пределах, которые при помощи нормального распределения и связанного с ним t-распределения определяются следующим выражением: (4) Величина является доверительным интервалом среднего значения Для серийных анализов обычно полагают Р = 0,95. . Таблица 1. значения коэффициента Стьюдента (t) f 1 2 3 4 5 6 7 8 9 10 11 12 Р=0,90 Р=0,95 Р=0,98 Р=0,99 6,31 2,92 2,35 2,13 2,02 1,94 1,90 1,86 1,83 1,81 1,80 1,78 12,7 4,30 3,18 2,78 2,57 2,45 2,36 2,31 2,26 2,23 2,20 2,18 31,8 6,97 4,54 3,75 3,37 3,14 3,00 2,90 2,82 2,76 2,72 2,68 63,6 9,93 5,84 4,60 4,03 3,71 3,50 3,36 3,25 3,17 3,11 3,05 Пример 1. Из десяти определений содержания марганца в пробе требуется подсчитать стандартное отклонение единичного анализа и доверительный интервал среднего значения Mn %: 0,69; 0,68; 0,70; 0,67; 0,67; 0,69; 0,66; 0,68; 0,67; 0,68. Решение. По формуле (1) подсчитывают среднее значение анализа =0,679 . Далее по формуле (2) находят стандартное отклонение единичного результата По табл. 1 (приложение) находят для f = n-1= 9 коэффициент Стьюдента (Р = 0,95) t = 2,26 и рассчитывают доверительный интервал среднего значения. По табл. 1 (приложение) находят для f=n-1=9 коэффициент Стьюдента (Р=0,95) t=2,26 и рассчитывают доверительный интервал среднего значения. Таким образом, среднее значение анализа определяется интервалом (0,679 ± 0,009) % Мn. Пример 2. Среднее из девяти измерений давления паров воды над раствором карбамида при 20°С равно 2,02 кПа. Выборочное стандартное отклонение измерений s=0,04кПа. Определить ширину доверительного интервала для среднего из девяти и единичного измерения, отвечающего 95%-й доверительной вероятности. Решение. Коэффициент Стьюдента t для доверительной вероятности 0,95 и f = 8 равен 2,31. Учитывая, что и найдем: , - ширина доверит. интервала для среднего значения - ширина доверит. интервала для единичного измерения значения Если же имеются результаты анализа образцов с различным содержанием, то из частных средних s путем усреднения можно вычислить общее среднее значение s. Имея m проб и для каждой пробы проводя nj параллельных определений, результаты представляют в виде таблицы: Номер анализа Номер образца 1 2 i…nj 1 x11 x12 x1i… 2 x21 x22 x2i… 3 x31 x32 x3i… … … … … j… … … … m … … … Средняя погрешность рассчитывают из уравнения: (5) со степенями свободыf = n – m, где n – общее число определений, n = m.nj. ЗАДАНИЕ. Вычислить среднюю ошибку определения марганца в пяти пробах стали с различным содержанием его. Значения анализа, % Mn: 1. 0,31 0,30 0,29 0,32 2. 0,51 0,57 0,58 0,57 3. 0,71 0,69 0,71 0,71 4. 0,92 0,92 0,95 0,95 5. 1,18 1,17 1,21 1,19 Сравнение средних результатов химического анализа. t-критерий Стьюдента Критерий Стьюдента (t) также используют при сравнении средних результатов химического анализа. Для этого рассчитывают выборочные средние случайную величину, равную их разности (для и и составляют удобства расчетов выбирают ). Далее находят стандартное отклонение этой величины Однако если сравнение выборочных дисперсий и с помощью F-критерия показала их однородность, лучшей оценкой обеих величин sА и sB может служить средневзвешенное стандартное отклонение: Тогда . Теперь можно оценить значимость расхождения средних и , назначив определенный (обычно 0,01 или 0,05) уровень значимости. Выборочные средние и значимо отличаются, если их разность превосходит свое стандартное отклонение более чем в ta,f раз, гдеta,f - коэффициент Стьюдента для доверительной вероятности P= 1-β; и числа степеней свободы объединенной выборки fА,В = nА + nB–2. На практике обычно вычисляют значение отношения: и сравнивают его с коэффициентом Стьюдента. Пример 1. Два аналитика (А и В), проводя анализ сплава на содержание Ве одинаковым методом, получили следующие результаты: n (число параллельных анализов) (средний результат), % s (выборочное стандартное отклонение), % B 5 7,32 0,13 A 4 7,44 0,105 Значимо ли расхождение средних результатов аналитиков для доверительной вероятности P = 0,95 (β = 0,05) Решение. Найдем критерия: значение средневзвешенного стандартного отклонения SА,В и t- что меньше, чем коэффициент Стьюдента (для f = 7 и P = 0,95 t= 2,37), следовательно, расхождение у двух аналитиков незначимо и оправдано случайным разбросом.