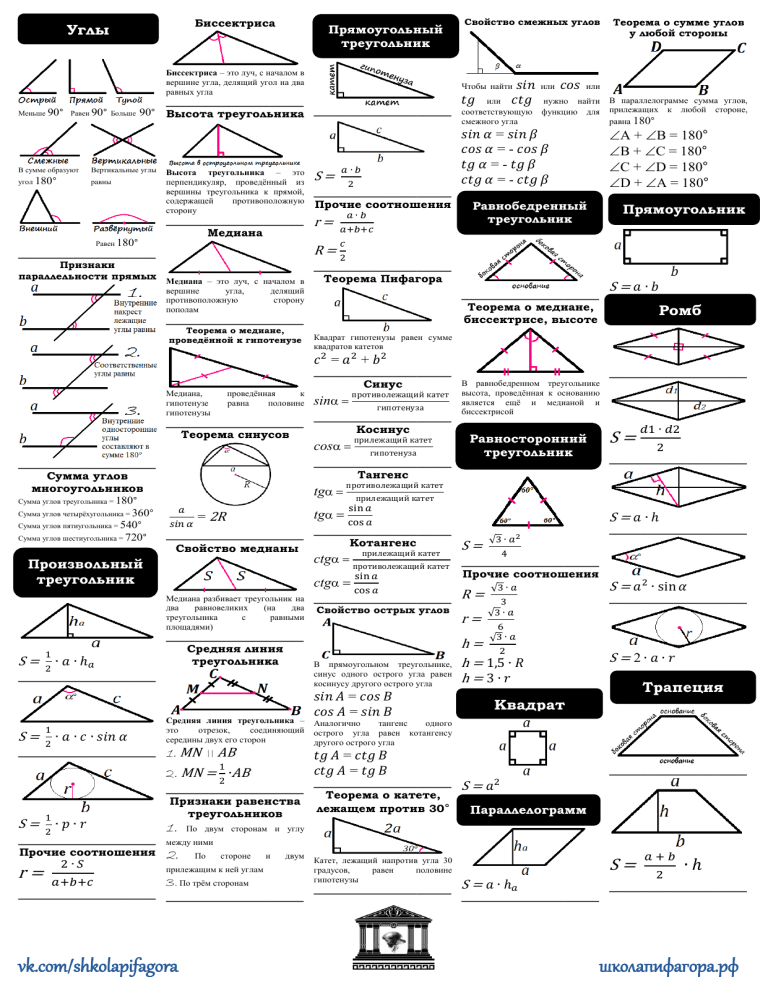
Биссектриса Углы Свойство смежных углов Прямоугольный треугольник Биссектриса – это луч, с началом в вершине угла, делящий угол на два равных угла ________________________ Меньше 90° Равен 90° Больше 90° Высота треугольника ________________________ В сумме образуют Вертикальные углы угол 180° равны 𝑎∙𝑏 2 ________________________ Высота треугольника – это перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону S= ________________________ r= Медиана Равен 180° ________________________ Признаки параллельности прямых Медиана – это луч, с началом в вершине угла, противоположную пополам Прочие соотношения 𝑎∙𝑏 𝑎+𝑏+𝑐 𝑐 R=2 ________________________ 𝑐𝑜𝑠 или 𝑡𝑔 нужно найти функцию для или соответствующую смежного угла или В параллелограмме сумма углов, прилежащих к любой стороне, равна 180° A + B = 180° B + C = 180° C + D = 180° D + A = 180° 𝑠𝑖𝑛 𝛼 = 𝑠𝑖𝑛 𝛽 𝑐𝑜𝑠 𝛼 = - 𝑐𝑜𝑠 𝛽 𝑡𝑔 𝛼 = - 𝑡𝑔 𝛽 𝑐𝑡𝑔 𝛼 = - 𝑐𝑡𝑔 𝛽 Равнобедренный треугольник Прямоугольник Теорема Пифагора делящий сторону S=𝑎∙𝑏 ________________________ Теорема о медиане, биссектрисе, высоте ________________________ Теорема о медиане, проведённой к гипотенузе 𝑠𝑖𝑛 𝑐𝑡𝑔 Чтобы найти Теорема о сумме углов у любой стороны Ромб Квадрат гипотенузы равен сумме квадратов катетов 𝑐 2 = 𝑎2 + 𝑏 2 ________________________ Медиана, гипотенузе гипотенузы проведённая к равна половине ________________________ Теорема синусов Произвольный треугольник sin противолежащий катет гипотенуза ________________________ Косинус cos прилежащий катет гипотенуза Свойство медианы Котангенс прилежащий катет ctgпротиволежащий катет sin 𝑎 cos 𝑎 Медиана разбивает треугольник на ________________________ два равновеликих (на два Свойство острых углов ctg с равными Средняя линия треугольника 1 ∙ 𝑎 ∙ ℎ𝑎 2 ________________________ В прямоугольном треугольнике, синус одного острого угла равен косинусу другого острого угла Средняя линия треугольника – это отрезок, соединяющий середины двух его сторон 1. MN AB 1 2. MN = 2 ∙AB Признаки равенства треугольников 1 ∙𝑝∙𝑟 1. По двум сторонам и углу 2 ________________________ между ними r= 2∙𝑆 𝑎+𝑏+𝑐 2 ________________________ 2. По стороне и двум прилежащим к ней углам 3. По трём сторонам ________________________ ________________________ vk.com/shkolapifagora S=𝑎∙ℎ √3 ∙ 𝑎 2 S= 4 ________________________ Прочие соотношения R= r= √3 ∙ 𝑎 3 √3 ∙ 𝑎 6 √3 ∙ 𝑎 2 h= h = 1,5 ∙ 𝑅 h=3∙𝑟 𝑠𝑖𝑛 𝐴 = 𝑐𝑜𝑠 𝐵 𝑐𝑜𝑠 𝐴 = 𝑠𝑖𝑛 𝐵 ________________________ S = 𝑎2 ∙ sin 𝛼 ________________________ S=2∙𝑎∙𝑟 Трапеция Квадрат Аналогично тангенс одного острого угла равен котангенсу другого острого угла 𝑡𝑔 𝐴 = 𝑐𝑡𝑔 𝐵 𝑐𝑡𝑔 𝐴 = 𝑡𝑔 𝐵 ________________________ Прочие соотношения 𝑑1 ∙ 𝑑2 прилежащий катет sin 𝑎 𝑎 tg = 2R cos 𝑎 𝑠𝑖𝑛 𝛼 ________________________ ________________________ S= S= S= противолежащий катет ________________________ 1 ∙ 𝑎 ∙ 𝑐 ∙ 𝑠𝑖𝑛 𝛼 2 ________________________ Равносторонний треугольник Тангенс tg треугольника площадями) S= ________________________ В равнобедренном треугольнике высота, проведённая к основанию является ещё и медианой и биссектрисой ________________________ ________________________ Сумма углов многоугольников Сумма углов треугольника = 180° Сумма углов четырёхугольника = 360° Сумма углов пятиугольника = 540° Сумма углов шестиугольника = 720° Синус ________________________ Теорема о катете, лежащем против 30° Катет, лежащий напротив угла 30 градусов, равен половине гипотенузы ________________________ ________________________ S=𝑎 2 Параллелограмм S= S = 𝑎 ∙ ℎ𝑎 𝑎+𝑏 2 ∙ℎ ________________________ ________________________ школапифагора.рф Средняя линия трапеции Диагонали в шестиугольнике Средняя линия трапеции – это отрезок, соединяющий середины боковых сторон трапеции Окружность 1. MN II a и MN II b Теорема об отрезках касательных Отрезки касательных к окружности, проведённых из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности Теорема об отношении площадей Прямая призма Отношение площадей подобных фигур равно квадрату коэффициента подобия 𝑎+𝑏 ________________________ 𝑆бол = 𝑘 2 2. MN = 2 Длина окружности 𝑆мал Круговой сектор ________________________ С = 2 ∙ 𝜋 ∙ 𝑅 ________________________ Теорема об отрезке на ________________________ Теорема об серединах диагоналей Площадь круга Прямоугольный параллелепипед отношении объёмов S = 𝜋 ∙ 𝑅2 V = 𝑆осн ∙ ℎ Sпов= 𝑆бок + 2𝑆осн Sбок = 𝑃осн ∙ ℎ ________________________ Центральный угол Sсектора = Отрезок, соединяющий середины диагоналей трапеции равен полуразности оснований lсектора = 𝑎−𝑏 EF = 2 ________________________ Теорема об описанной Центральный угол равен градусной мере дуги, на которую он окружности опирается 𝑙сектора ∙ 𝑅 2 2 ∙ 𝑆сектора 𝑅 Векторы Отношение объёмов подобных фигур равно кубу коэффициента подобия 𝑉бол 𝑉мал = 𝑘3 V=𝑎∙𝑏∙ℎ 𝑆пов = 2𝑎𝑏 + 2𝑏ℎ + 2𝑎ℎ 𝑑 2 = 𝑎2 + 𝑏 2 + ℎ2 Сложение векторов Конус ________________________ Цилиндр Вписанный угол Если трапецию можно вписать в окружность, то эта трапеция – равнобедренная ________________________ Теорема о перпендикулярных диагоналях Вписанный угол равен половине градусной мере дуги, на которую он опирается Даны два вектора. К концу первого пристраиваем начало второго. Теперь соединяем начало первого и конец второго. Это и есть сумма векторов 𝑎⃗ и 𝑏⃗⃗ Подобие ________________________ Теорема о касательной 1 V = 3 ∙ 𝜋 ∙ 𝑅2 ∙ ℎ Sпов= 𝜋 ∙ 𝑅 ∙ (𝑅 + 𝑙) Sбок = 𝜋 ∙ 𝑅 ∙ 𝑙 Куб Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований h= 𝑎+𝑏 2 Касательная к окружности перпендикулярна к радиусу, проведённому в точку касания ________________________ Шестиугольник Теорема о вписанном 4-ке A = A1, B = B1, C = C1 𝐴1 𝐵1 𝐵1 𝐶1 𝐴1 𝐶1 = 𝐵𝐶 = 𝐴𝐶 =k 𝐴𝐵 ________________________ Признаки подобия треугольников 1. 2. По двум равным углам По двум пропорциональным сторонам и углу между ними В любом вписанном в окружность четырёхугольнике сумма противоположных углов равна 3. V= Теорема об описанном 4-ке R= 𝑎 √3 ∙ 𝑎 r= 2 ________________________ Sбок = 2 ∙ 𝜋 ∙ 𝑅 ∙ ℎ V = 𝑎3 Sпов= 6𝑎2 d = √3𝑎 Sтр = √3 ∙ 𝑎2 4 Шар Октаэдр По трём пропорциональным сторонам Отношение периметров, биссектрис, медиан, высот и серединных перпендикуляров равно коэффициенту подобия 𝑝 (периметры) 𝑝бол = k Площади в шестиугольнике 𝜋 ∙𝑑 2 ∙ℎ 4 Sпов = 2 ∙ 𝜋 ∙ 𝑅 ∙ (𝑅 + ℎ) 3√3 ∙ 𝑎2 ________________________ 180° Отношения в 2 ________________________ 𝛼 + 𝛽 = 180° подобных Прочие соотношения ________________________ треугольниках S= V = 𝜋 ∙ 𝑅2 ∙ ℎ 4 Sпов= 2 ∙ √3 ∙ 𝑎2 V = 3 ∙ 𝜋 ∙ 𝑅3 Sпов= 4 ∙ 𝜋 ∙ 𝑅 2 ________________________ Пирамида мал (биссектрисы) 𝑙бол 𝑙мал =k 𝑚бол В любом описанном окружностью (медианы) =k 𝑚мал четырёхугольнике суммы ℎбол противоположных сторон равны (высоты) ℎ = k 𝑎+𝑐=b+d мал ℎсер бол 𝑝∙𝑟 Sпр = √3 ∙ 𝑎2 S = 2 1 V = 3 ∙ 𝑆осн ∙ ℎ (сер.перпендикуляр) ℎ =k Sпов= 𝑆бок + 𝑆осн сер мал ________________________ ________________________ ________________________ ________________________ vk.com/shkolapifagora школапифагора.рф