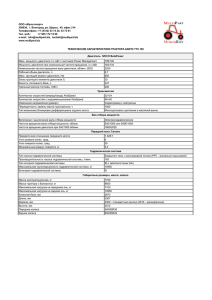
Оглавление 1 Исходные данные ....................................................................................... 3 2. Выбор двигателя ....................................................................................... 3 2.1. Выбор двигателя по мощности.......................................................... 4 2.2 Предварительная проверка выбора двигателя по моментам........... 5 3 Кинематический расчёт ............................................................................. 6 3.1 Определение общего передаточного отношения ............................. 6 3.2 Разбиение общего передаточного отношения по ступеням ............ 7 3.3 Ограничитель угла поворота выходного вала .................................. 7 3.4 Определение чисел зубьев зубчатых колес ....................................... 8 4 Силовой расчёт ЭМП ................................................................................. 9 5 Расчёт зубчатых колёс на прочность ..................................................... 10 5.1 Выбор материала................................................................................ 10 5.2 Расчет зубчатых передач на изгибную прочность ......................... 11 6. Геометрический расчёт .......................................................................... 13 7. Проектный расчет валов ......................................................................... 18 8. Подбор шариковых подшипников ........................................................ 24 9. Проверочные расчеты ............................................................................. 26 9.1 Проверочный расчет на точность ........................................................ 26 9.2 Проверка правильности выбора двигателя ........................................ 33 9.3 Проверочные расчеты на прочность ................................................... 36 Список литературы ..................................................................................... 40 1 Исходные данные В данном домашнем задании необходимо разработать электромеханический привод (ЭМП) согласно техническому заданию. Начальные данные для проектирования приведены в таблице 1. Таблица 1. Исходные данные Момент нагрузки Мн Частота вращения выходного вала 𝒏 Угловое ускорение вращения выходного вала Ен Момент инерции нагрузки Jн Температура эксплуатации 𝑇э Род тока Срок службы не менее 𝐿 Критерий расчета Режим работы Метод расчета, процент риска при расчете, точность Рабочий угол поворота выходного вала Точность отработки не хуже Примечание 1,25 Н·М 15 об/мин 5 рад/с2 0,5 кг·м2 ±50 °С постоянный 100 час минимизация погрешности кратковременный вероятностный 0.27% ±1080 град 15' нет 2. Выбор двигателя В общем случае электромеханический привод состоит из трёх основных звеньев (см. рисунок 1). Рисунок 1. Схема разрабатываемой конструкции Целью расчета является выбор двигателя для ЭМП. 2.1. Выбор двигателя по мощности Расчётная мощность электродвигателя определяется по формуле: Pн (2.1) , ηо — расчётная мощность нагрузки; ηо — КПД передач цепи Pр = ξ где Pн = 𝑀н ∙ 𝜔вых двигатель-нагрузка; ξ – коэффициент запаса. Учитывая, что Мн = 1,25Н ∙ м — статический момент нагрузки, а 𝜔вых = 𝜋 30 ∙ 𝑛 — угловая скорость вращения нагрузки и приняв КПД передачи ηо = 0,8 для предварительных расчетов и коэффициент запаса для приводов с переменной нагрузки ξ = 1,3, расчётная мощность электродвигателя: 𝜋𝑛 𝑀н ∙ 𝑀н ∙ 𝜔вых 30 = 1,3 ∙ 1,25 ∙ 𝜋 ∙ 15 = 3,19Вт Pр = ξ =ξ ηо ηо 0,8 ∙ 30 Предварительно выберем двигатель ДПР-52-Ф1-03, который имеет следующие параметры: Таблица 2. Основные параметры двигателя Номинальная мощность Номинальный момент Пусковой момент Номинальная частота вращения Момент инерции ротора Напряжение питания Время работы Масса Pном Mном Mпуск nном Jр U Tч m 4,6 Вт 9,8 Н∙мм 54 Н∙мм 4500 об/мин 1,7∙10-6 кг∙м2 27 В 2500 ч 0,25 кг В обозначение двигателя входит 52 – номер габарита, Ф1 – крепление за фланец. Исполнение электродвигателя представлено на рисунке 2. 4 Рисунок 2 – Чертеж электродвигателя серии ДПР-52 Проверим, ξ= Pном Pp = 4,6 3,2 = 1,44 – значение коэффициента запаса удовлетворяет рекомендуемым значениям приводом с переменной нагрузкой. 2.2 Предварительная проверка выбора двигателя по моментам Проверка проводится по условию Mс. пр. +Mд. пр. < Mпуск. Статический приведённый момент определяется по формуле: Mс. пр. = ξ Mн , io · η о (2.2) где Mн – момент нагрузки; iо – общее передаточное отношение; ηо — КПД передач цепи двигатель-нагрузка. Динамический приведённый момент определяется по формуле: Jн Mд. пр. = εдв · (Jдв + Jр + 2 ) iо 5 (2.3) где εн – угловое ускорение вращения на выходном звене; iо – общее передаточное отношение; Jдв – момент инерции двигателя; Jр – момент инерции редуктора; Jн – момент инерции нагрузки. Общее передаточное отношение: iо = где ωдв = 𝜋 30 𝜔вых = ωдв 𝜔вых (2.4) ∙ 𝑛ном – угловая скорость вращения нагрузки двигателя; 𝜋 30 ∙ 𝑛 – угловая скорость вращения нагрузки. Тогда 𝑖𝑜 = 𝑛ном 4500 = = 300. 𝑛 15 1,25 ∙ 103 Mс. пр. = 1,3 = 6,7 Н ∙ мм; 300 · 0,8 Mд. пр. = 5 ∙ 300 ∙ (1,7 ∙ 10−6 + 1,7 ∙ 10−6 + 0,5 ) = 13,4 Н ∙ мм; 3002 Mс. пр. + Mд. пр = 6,7 + 13,4 = 20,1 Н ∙ мм Проверка 20,1 < Mпуск = 54 Нмм выполняется. 3 Кинематический расчёт Целью расчёта является разработка кинематической схемы привода, разбиение передаточного отношения, определения числа зубьев зубчатых колес. 3.1 Определение общего передаточного отношения Общее передаточное отношение: iо = где ωдв = 𝜋 30 𝜔вых = ωдв 𝜔вых ∙ 𝑛ном – угловая скорость вращения нагрузки двигателя; 𝜋 30 ∙ 𝑛 – угловая скорость вращения нагрузки. Тогда 𝑖𝑜 = 𝑛ном 4500 = = 300. 𝑛 15 6 (3.1) 3.2 Разбиение общего передаточного отношения по ступеням Согласно условию ТЗ проектирование будет осуществляться по критерию минимальной погрешности. Число ступеней редуктора в таком случае: n = 1,4 lg(𝑖0 ) ; (3.2) где iо — общее передаточное отношение цепи. Тогда: n = 1,4 lg(300) = 3,5 ≈ 3 В первом приближении, передаточное отношение каждой ступени равно 𝑖𝑖 = 𝑛√𝑖0 (3.3) 3 𝑖𝑖 = √300 = 6,69. При этом следует выбирать такие передаточные отношения, что бы выполнялось следующее условие: 𝑖1−2 ≤ 𝑖3−4 ≤ 𝑖5−6 . Передаточные отношения ступеней сведены в таблицу 3 Таблица 3. Передварительные передаточные отношения № зацепления i 1-2 5 3-4 6,6 5-6 9 3.3 Ограничитель угла поворота выходного вала Для обеспечения отключения двигателя при повороте выходного вала на угол, превышающий допустимый (±1080 град), в конструкции необходимо предусмотреть концевые выключатели. Концевой выключатель размещается так, чтобы движущийся элемент гарантированно задевал его актуатор, достигая заданной точки. В данной конструкции используются два малогабаритных однополюсных микропереключателя с одинарным разрывом цепи МП1-1 (рис.3), предназначенные для коммутации электрических цепей постоянного и переменного тока при напряжении не более 250 В и силе тока до 2,0 А. 7 Рисунок 3 – Кинематическая схема ЭМП Ограничителем является дополнительный вал, передаточное отношение зацепления которого выбирается с учетом рекомендуемого ряда числа зубьев и рабочего угла проворота вала: 𝑖4 = 1080 = 9. 120 Таблица 4. Передаточные отношения № зацепления i 1-2 5 3-4 6,6 5-6 9 7-8 9 3.4 Определение чисел зубьев зубчатых колес Число зубьев колеса рассчитывается по формуле: zк = zш · ij , (3.4) где zш — число зубьев шестерни; ij — передаточное отношение одной ступени. Назначим количества зубьев колес и шестерен из стандартного ряда: Таблица 5. Числа зубьев колес редуктора Номер ступени Передаточное отношение ij 1 2 3 4 5 6,6 9 9 Назначенные числа зубьев 8 Шестерня Колесо 20 20 20 20 100 132 180 180 Погрешность фактического передаточного отношения, не включая ступень ограничителя, от расчетного не должна превышать 10 процентов: 𝑖0 − Пij 300 − 5 ∙ 6,6 ∙ 9 𝛥𝑖 = | | ∙ 100% = | | ∙ 100% = 1%. 𝑖0 300 В таком случае можно считать выбранные значения чисел зубьев колеса и шестерни подходящими для Кинематическая схема приведена на рисунке: Рисунок 4 – Кинематическая схема ЭМП 4 Силовой расчёт ЭМП Целью силового расчёта является определение возникающих в каждой передаче моментов. Моменты рассчитываются по формуле: Mведущ = Mведом ij · ηj · ηподш (4.1) где Mведущ — момент на ведущем звене; Mведом — момент на ведомом звене; ij — передаточное отношение ступени; ηj — КПД передачи, примем равным 0,98; ηподш — КПД подшипников, примем равным 0,99. По кинематической схеме, в редукторе 4 вала, ведем расчёт последовательно к валу двигателя: 9 М𝑉𝐼 = Мн + Мд = Мн + 𝐽н · εн, (4.2) где Mн – момент нагрузки; Mд – динамический момент нагрузки; Jн – момент инерции нагрузки; εн –угловое ускорение вращения выходного вала. Тогда М𝐼𝑉 = 1,25 + 0,5 · 5 = 3,75 Н · м М𝐼𝐼𝐼 = М𝐼𝑉 3,75 = = 0,43 Н ∙ м, i3 · ηj · ηподш 9 · 0,98 · 0,99 М𝐼𝐼 = М𝐼𝐼𝐼 0,43 = = 0,067 Н ∙ м; i2 · ηj · ηподш 6,6 · 0,98 · 0,99 М𝐼 = М𝐼𝐼 0,067 = = 0,0138 Н ∙ м. i1 · ηj · ηподш 5 · 0,98 · 0,99 5 Расчёт зубчатых колёс на прочность Целью расчёта является определение модуля зацепления зубчатых колёс, обеспечивающего работоспособность в течение заданного срока службы. 5.1 Выбор материала Для цилиндрической передачи открытого типа с небольшими окружными скоростями в качестве материала для шестерен будет использоваться углеродистая сталь 35, а в качестве материала для колёс — сталь 45. Зубья шестерен будут выполнены из материалов с более высокой твёрдостью рабочих поверхностей по сравнению с колёсами для повышения долговечности зубчатой передачи. Основной причиной выхода их строя открытых передач является поломка зубьев в результате усталости материала. Для предотвращения поломок зубья рассчитывают на изгибную прочность. 10 Таблица 6. Характеристики используемых материалов Шестерня Колесо сталь 45 сталь 35 Материал Модуль упругости E, Мпа 2·105 Коэффициент линейного расширения α·10-6, 1/°C 12 Плотность ρ, г/см3 7,85 Твёрдость 240 Термообработка 250 Поверхностная обработка Предел прочности σв, Мпа 580 520 Предел текучести σт, Мпа 360 250 Предел выносливости материала: 𝜎−1 = [0,33σв + (70 … 120)]. (5.1) Примем поправочное слагаемое равным 90, тогда 𝜎−1 сталь45 = 0,33 ∙ 580 + 90 = 281 МПа; 𝜎−1 сталь35 = 0,33 ∙ 520 + 90 = 238,5 МПа. Допускаемое напряжение: [σF] = 𝜎−1 , 𝑛 (5.2) где 𝑛 = 1,5 – коэффициент запаса. Тогда [σF] сталь45 = [σF]сталь35 = 281 = 187; 1,5 238,5 = 175. 1,5 5.2 Расчет зубчатых передач на изгибную прочность Для открытых передач модуль зацепления определяется из изгибной прочности: 3 m= √ M · YF · 2K , z · ψm · [σF] 11 (5.3) где M — крутящий момент, действующий на рассчитываемое колесо; YF — коэффициент формы зуба для прямозубых цилиндрических колёс; z — число зубьев рассчитываемого колеса; K = 1,3 — коэффициент расчётной нагрузки; ψm = 10 — коэффициент ширины зубчатого венца для мелкомодульных передач; [σF] — максимальное допускаемое напряжение изгиба. Для каждой передачи расчёт производится по тому зубчатому колесу (из пары шестерня – зубчатое колесо), для которого отношение YF/[σF] больше. Таблица 7. Определение отношения YF/[σF] № (п/п) 1 2 3 Числа зубьев Шестерня 20 20 20 Коэффициент формы YF Колесо 100 132 180 Шестерня 4,15 4,15 4,15 Колесо 3,75 3,75 3,75 YF/[σF] Шестерня 0,022 0,022 0,022 Колесо 0,021 0,021 0,021 Из таблицы 7 следует, что расчет следует проводить по колесам. 3 m12 = √ 3 13,8 · 3,75 · 2 · 1,3 M · YF · 2K =√ = 0,16 мм; z · ψm · [σF] 20 · 10 · 187 3 m34 = √ 3 m56 = √ 67 · 4,15 · 2 · 1,3 = 0,27 мм; 20 · 10 · 187 430 · 4,15 · 2 · 1,3 = 0,49 мм. 20 · 10 · 187 Значения модулей зацепления округляются в соответствии с ГОСТ 956360, а также учитывая конструктивные особенности изделия. Таким образом, модули зацепления цилиндрических зубчатых передач примем m12 = 0,4; m34 = 0,4; m56 = 0,5. Модуль зацепления передачи ограничителя выбирается m56 = 0,3 из геометрических соображений. 12 6. Геометрический расчёт Целью расчёта является определение основных размеров передач и их элементов. Основные геометрические размеры цилиндрических зубчатых передач указаны на рисунке 4. Рисунок 5 - Геометрические параметры цилиндрической зубчатой передачи В данном приводе используются цилиндрические прямозубые передачи, поэтому угол наклона зубьев β = 0°. Делительный диаметр определяется соотношением: m·z d= , cos β (6.1) где m — модуль зацепления рассчитываемой пары колёс; z — число зубьев рассчитываемого колеса; β = 0° — угол наклона зубьев. Диаметр вершин зубьев определяется по формуле: da = d + 2m(h∗a + x), (6.2) где d — делительный диаметр; m — модуль зацепления рассчитываемой пары колёс; β = 0° — угол наклона зубьев; h∗a = 1 — коэффициент высоты головки зуба; x = 0 — коэффициент смещения. Диаметр впадин определяется по формуле: df = d − 2m(h∗a + c ∗ − x), (6.3) где m — модуль зацепления рассчитываемой пары колёс; d — делительный диаметр; β = 0° — угол наклона зубьев; h∗a = 1 — коэффициент высоты головки зуба; c* = 0,5 — коэффициент радиального зазора m ≤ 0,5 мм по ГОСТ 958781; x = 0 — коэффициент смещения. Ширина колеса определяется по формуле: bк = ψm · m, (6.5) где ψm = 10 — коэффициент ширины зубчатого венца для мелкомодульных передач; m — модуль зацепления рассчитываемой пары колёс. Ширина шестерни определяется по формуле: bш = bк + (1. .2)m, (6.6) где bк — ширина колеса; m — модуль зацепления рассчитываемой пары колёс. 1. Шестерня 1 0,4 · 20 = 8 мм; 1 da1 = 8 + 2 ∙ 0,4 ∙ (1 + 0) = 8,8 мм; d1 = df1 = 8 − 2 ∙ 0,4 ∙ (1 + 0,5 − 0) = 6,8 мм; bш1 = 4 + 1 ∙ 0,4 = 4,4 мм. 2. Зубчатое колесо 1 0,4 · 100 = 40 мм; 1 da2 = 40 + 2 ∙ 0,4 ∙ (1 + 0) = 40,8 мм; d2 = df2 = 40 − 2 ∙ 0,4 ∙ (1 + 0,5 − 0) = 38,8 мм; bк2 = 10 · 0,4 = 4 мм. 3. Шестерня 2 0,4 · 20 = 8 мм; 1 da3 = 8 + 2 ∙ 0,4 ∙ (1 + 0) = 8,8 мм; d3 = df3 = 6 − 2 ∙ 0,4 ∙ (1 + 0,5 − 0) = 6,8 мм; 14 bш3 = 4 + 1 ∙ 0,4 = 4,4 мм. 4. Зубчатое колесо 2 0,4 · 132 = 52,8 мм; 1 da4 = 52,8 + 2 ∙ 0,4 ∙ (1 + 0) = 53,6 мм; d4 = df4 = 52,8 − 2 ∙ 0,4 ∙ (1 + 0,5 − 0) = 51,6 мм; bк4 = 10 · 0,4 = 4 мм. 5. Шестерня 3 0,5 · 20 = 10 мм; 1 da5 = 10 + 2 ∙ 0,5 ∙ (1 + 0) = 10,6 мм; d5 = df5 = 10 − 2 ∙ 0,5 ∙ (1 + 0,5 − 0) = 8,5 мм; bш5 = 5 + 1 ∙ 0,5 = 5,5 мм. 6. Зубчатое колесо 3 0,5 · 180 = 90 мм; 1 da6 = 90 + 2 ∙ 0,5 ∙ (1 + 0) = 90,6 мм; d6 = df6 = 90 − 2 ∙ 0,5 ∙ (1 + 0,5 − 0) = 88,5 мм; bк6 = 10 · 0,5 = 5 мм. 7. Шестерня 4 0,3 · 20 = 6 мм; 1 da7 = 6 + 2 ∙ 0,3 ∙ (1 + 0) = 6,6 мм; d7 = df7 = 6 − 2 ∙ 0,3 ∙ (1 + 0,5 − 0) = 5,1 мм; bш7 = 3 + 1 ∙ 0,3 = 3,3 мм. 8. Зубчатое колесо 4 0,6 · 180 = 54 мм; 1 da8 = 54 + 2 ∙ 0,3 ∙ (1 + 0) = 54,6 мм; d8 = df8 = 54 − 2 ∙ 0,3 ∙ (1 + 0,5 − 0) = 53,1 мм; bк8 = 10 · 0,3 = 3 мм. 15 Окружной шаг определяется по формуле: p = m · π, (6.4) где m — модуль зацепления рассчитываемой пары колёс. p1 = p2 = 0,4 · π = 1,26 мм; p3 = p4 = 0,4 · π = 1,26 мм; p5 = p6 = 0,5 · π = 1,57 мм; p7 = p8 = 0,3 · π = 0,94 мм. Межосевое расстояние определяется по формуле: aω = 0,5 · m · (zк + zш) , cos β (6.7) где m — модуль зацепления рассчитываемой пары колёс; zк — число зубьев колеса; zш — число зубьев шестерни; β = 0° — угол наклона зубьев. 0,5 · 0,4 · (100 + 20) = 24 мм; 1 0,5 · 0,4 · (132 + 20) aω34 = = 30,4 мм; 1 0,5 · 0,5 · (180 + 20) aω56 = = 50 мм; 1 0,5 · 0,3 · (180 + 20) aω56 = = 30 мм. 1 aω12 = В таблице 8 приведены все рассчитанные геометрические параметры зубчатых колес. Таблица 8. Геометрические параметры зубчатых колес № колеса 1 2 3 4 5 6 7 8 Z 20 100 20 132 20 180 20 180 m 0,4 0,4 0,5 0,3 d, мм da, мм 8 40 8 52,8 10 90 6 54 8,8 40,8 8,8 53,6 10,6 90,6 6,6 54,6 16 df, мм 6,8 38,8 6,8 51,6 8,5 88,5 5,1 53,1 b, мм 4,4 4 4,4 4 5,5 5 3 3,3 a , мм p 24 1,26 30,4 1,26 50 1,57 30 0,94 По расчетным данным проводится компоновка редуктора (рис 6,7). Рисунок 6 – Компоновка редуктора (вид сверху) Рисунок 7 – Компоновка редуктора (вид А-А) 17 7. Проектный расчет валов Составим таблицу исходных данных для валов в соответствии с компоновкой (табл.9). Таблица 9 – Исходные данные № вала 2 3 4 M, Нмм 67 430 3750 𝑑1 , мм 40 10 90 𝑑2 , мм 8 52,8 - 𝑙1 , мм 3,8 10,4 17 𝑙2 , мм 11,3 6,1 10,3 𝑙3 , мм 16 15,1 21,3 Примем для вала сталь 40Х со следующими характеристиками: Тбалица 10 – Характеристики материала вала Марка 𝜎в Термообработка стали МПа 45 Улучшение 580 Твердость 𝜎-1 Примечания ГОСТ Мпа (ср. значение) не стойкие 250 240 НВ 4543-71 коррозионно 7.1 Расчёт IV вала Определим значения сил, приложенных к зубчатому колесу: окружная сила Ft 𝐹𝑡1 = 2 𝑀 3750 =2 = 83,3 Н; 𝑑1 90 радиальная сила Fr: 𝐹𝑟1 = 𝐹𝑡1 ∙ cos(𝛼 ) = 30,3 Н; Рассчитаем изгибающие моменты в сечениях вала. Реакции опор: 𝑅𝑎𝑥 = 𝐹𝑡1 𝑙3 = 56,2 𝐻; (𝑙2 + 𝑙3 ) 𝑅𝑏𝑥 = 𝐹𝑡1 𝑙2 = 27,2 𝐻; (𝑙2 + 𝑙3 ) 𝑅𝑎𝑦 = 𝐹𝑟1 𝑙3 = 20,4𝐻. (𝑙2 + 𝑙3 ) 𝑅𝑏𝑦 = 𝐹𝑟1 𝑙2 = 9,9 𝐻; (𝑙2 + 𝑙3 ) Изгибающий момент в опасном сечении 𝐶: 2 + 𝑀 2 = √2112 + 5792 = 616 Нмм. 𝑀пр из = √𝑀𝑥𝑐 𝑦𝑐 Диаметр вала по приведенному изгибающему моменту в наиболее опасном сечении вала: 3 𝐷4 ≥ √ где 𝜎𝑓 = 𝜎−1 1.5 𝑀пр из , 0,1 𝜎𝑓 (7.1) = 252 МПа. 3 𝐷4 = √ 616 = 2,9 мм. 0,1 ∙ 252 Примем 𝐷4 = 3 мм. Чтобы обеспечить нормальную работу передач с заданной точностью, необходимо также обеспечить достаточную жесткость валиков на скручивание и изгиб. Из-за скручивания валиков под действием крутящих моментов в передачах возникает упругий мертвый ход: ∆𝜑 = 2 ∙ М ∙ 𝑙𝑟𝑎𝑏 ≤ [𝜑 ], 𝐺∙𝐽 19 (7.2) где 𝑙𝑟𝑎𝑏 = 27,3 мм – длина рабочего участка, 𝐺 = 80 Гпа – модуль упругости при сдвиге кручением стали 40Х, 𝐽 = 𝜋 32 ∙ 𝐷4 . Допускаемое значение угла закручивания валика составляет [𝜑] = 5 … 30 угловых минут. ∆𝜑 = 2 ∙ 3750 ∙ 27,3 = 322, 80 ∙ 7,95 следовательно, необходимо увеличить диаметр вала. Примем 𝐷4 = 7 мм, тогда ∆𝜑 = 10,9 угловых минут и условие выполняется. Проверка размеров вала из условия изгибной жёсткости: 𝑓𝑟𝑎𝑠 ≤ 𝑓𝑝𝑟𝑒𝑑 , где (7.3) 𝑓𝑝𝑟𝑒𝑑 = (0,0002 … 0,0003)𝑙 = 0,0097 … 0,015 мм – предельно допускаемая величина прогиба, 𝑓𝑟𝑎𝑠 – расчётная величина прогиба валика в месте установки колеса или шкива (𝐸 = 2 ∙ 105 , 𝐽 = 𝜋 64 ∙ 𝐷4 = 118). Прогиб вычисляется по правилу Верещагина с построением эпюр от единичной силы: Рисунок 8 – Схема расчета прогибов вала IV 𝑓𝑥 = 1 1 2 (𝑀𝑥 ∙ 𝑙2 ∙ ∙ ℎ ∙ ) = 0,00058 мм; 𝐸∙𝐽 2 3 𝑓𝑦 = 1 1 2 (𝑀𝑦 ∙ 𝑙2 ∙ ∙ ℎ ∙ ) = 0,00021 мм; 𝐸∙𝐽 2 3 Тогда: 20 𝑓𝑟𝑎𝑠 = √𝑓𝑥 2 + 𝑓𝑦 2 = 0,00062 мм, 𝑓𝑟𝑎𝑠 ≤ 𝑓𝑝𝑟𝑒𝑑 , следовательно, условие выполняется и диаметр вала оставляем равным 7 мм. 7.2 Расчёт III вала Расчет проводится аналогично 7.1.Определим значения сил, приложенных к зубчатому колесу: окружная сила Ft 𝐹𝑡1 = 2 ∙ 𝐹𝑡2 = 2 ∙ 430 = 86 Н; 10 430 = 16,3 Н. 52,8 радиальная сила Fr: 𝐹𝑟1 = 86 ∙ 0,4 = 31,3 Н; 𝐹𝑟2 = 16,3 ∙ 0,4 = 5,9 Н. Рассчитаем изгибающие моменты в сечениях вала. Реакции опор: 𝑅𝑎𝑥 = 𝐹𝑡1 (𝑙2 + 𝑙3 ) + 𝐹𝑡1 𝑙3 = 65,7 𝐻; 𝑙 𝑅𝑏𝑥 = 𝐹𝑡2 (𝑙1 + 𝑙2 ) + 𝐹𝑡1 𝑙1 = 36,6 𝐻; 𝑙 𝑅𝑎𝑦 = 𝐹𝑟1 (𝑙2 + 𝑙3 ) − 𝐹𝑟1 𝑙3 = −18,2 𝐻. 𝑙 𝑅𝑏𝑦 = 𝐹𝑟2 (𝑙1 + 𝑙2 ) − 𝐹𝑟1 𝑙1 = −7,2 𝐻; 𝑙 Изгибающий момент в опасном сечении: 2 + 𝑀 2 = √189,42 + 559,62 = 709 Нмм. 𝑀пр из = √𝑀𝑥𝑐 𝑦𝑐 21 Диаметр вала по приведенному изгибающему моменту в наиболее опасном сечении вала: 3 𝐷3 ≥ √ где 𝜎𝑓 = 𝜎−1 1.5 𝑀пр из 3 709 =√ = 3 мм, 0,1 𝜎𝑓 0,1 ∙ 252 = 252 МПа. Примем 𝐷3 = 4 мм. Чтобы обеспечить нормальную работу передач с заданной точностью, необходимо также обеспечить достаточную жесткость валиков на скручивание и изгиб. Из-за скручивания валиков под действием крутящих моментов в передачах возникает упругий мертвый ход: ∆𝜑 = 2 ∙ М ∙ 𝑙𝑟𝑎𝑏 ≤ [𝜑 ], 𝐺∙𝐽 где 𝑙𝑟𝑎𝑏 = 6,1 мм – длина рабочего участка, 𝐺 = 80 Гпа – модуль упругости при сдвиге кручением стали 40Х, 𝐽 = 𝜋 32 ∙ 𝐷 4 = 25,1. Допускаемое значение угла закручивания валика составляет [𝜑] = 5 … 30 угловых минут. ∆𝜑 = 2 ∙ 430 ∙ 6,1 = 8,24, 80 ∙ 25,1 следовательно, условие выполняется. Проверка размеров вала из условия изгибной жёсткости: 𝑓𝑟𝑎𝑠 ≤ 𝑓𝑝𝑟𝑒𝑑 , где 𝑓𝑝𝑟𝑒𝑑 = (0,0002 … 0,0003)𝑙 = 0,0064 … 0,0095 мм – предельно допускаемая величина прогиба, 𝑓𝑟𝑎𝑠 – расчётная величина прогиба валика в месте установки колеса или шкива (𝐸 = 2 ∙ 105 , 𝐽 = 𝜋 64 ∙ 𝐷4 = 3,98). Прогиб вычисляется по правилу Верещагина с построением эпюр от единичной силы: 22 Рисунок 9 – Схема расчета прогибов вала III 𝑓𝑥 = 1 1 1 1 (𝑀𝑥𝑐 ∙ 𝑙1 ∙ ∙ ℎ0.67 + (𝑀𝑥𝑐 − 𝑀𝑥𝑑 ) ∙ 𝑙2 ∙ ∙ ℎ0.89 + 𝑀𝑥𝑑 ∙ 𝑙2 ∙ ℎ0.86 + 𝑀𝑥𝑑 ∙ 𝑙3 ∙ ∙ ℎ0.45 ) 𝐸∙𝐽 2 2 2 = −0,016 мм; 𝑓𝑦 = 1 1 1 1 (𝑀𝑦𝑐 ∙ 𝑙1 ∙ ∙ ℎ0.67 + (𝑀𝑦𝑐 − 𝑀𝑦𝑑 ) ∙ 𝑙2 ∙ ∙ ℎ0.89 + 𝑀𝑦𝑑 ∙ 𝑙2 ∙ ℎ0.86 + 𝑀𝑦𝑑 ∙ 𝑙3 ∙ ∙ ℎ0.45 ) 𝐸∙𝐽 2 2 2 = 0,067 мм; Тогда 𝑓𝑟𝑎𝑠 = √𝑓𝑥 2 + 𝑓𝑦 2 = 0,068 мм, что не удовлетворяет условию. Увеличим диаметр вала до 5 мм, тогда 𝑓𝑟𝑎𝑠 = 0,0068 ≤ 𝑓𝑝𝑟𝑒𝑑 и условие выполняется. Так как для второго вала крутящий момент намного меньше чем на третьем валу, примем его диаметр равным 𝐷2 = 4 мм. 23 8. Подбор шариковых подшипников Подберем радиальные шарикоподшипники для опор вала по динамической грузоподъемности: (𝐶)𝑝 = 0.01 ∙ 𝑃 ∙ 3√60 ∙ 𝑛 ∙ 𝐿ℎ , (8.1) где 𝐿ℎ = 100 ч – долговечность, 𝑛 = 15 об/мин – частота вращения, 𝑃 – эквивалентная динамическая нагрузка. 𝑃 = (𝑋 ∙ 𝑉 ∙ 𝐹𝑟 + 𝑌 ∙ 𝐹𝑎1 ) ∙ 𝑘𝑏 ∙ 𝑘𝑡 (8.2) При вращающемся внутреннем кольце V=1, при возможных перегрузках до 200% расчетной нагрузки – 𝑘𝑏 = 2, при температуре в подшипниках до +60oС – 𝑘𝑡 = 1. Силы в опорах 𝐹𝑅 = √𝑅𝑥2 + 𝑅𝑦2 . Значения X и Y табличные. Таблица 11 – Данные рассчета подшипников № вала 2 3 4 𝐷 4 5 10 𝐹𝑅𝑎 , Н 11,7 68,2 59,8 𝐹𝑅𝑏 , Н 8,99 37,3 28,9 𝑃 22,2 129 113 Тип подшипника 1000092 1000093 1000096 (𝐶)𝑝 38,8 120 50,6 Подшипник для опор: Таблица 12 – Параметры радиальных однорядных шарикоподшипников Условное обозначение 1000092 Основные размеры, мм d D B r Dw Лёгкая серия диаметров 2 2 6 2,3 0,2 1,000 Со Н Z C Н 7 220 90 1000093 3 8 3 0,2 1,588 6 440 200 1000096 6 15 5 0,4 2,381 8 1160 570 Момент трения в подшипнике на опоре: 𝑀𝑡𝑟 = 𝑀0𝑎 + 1,25𝐹𝑟 ∙ 𝑓 ∙ где 𝑀0𝑎 = 0,4𝐷0 , 𝐷0 = самой нагруженной опоры. 𝐷+𝑑 2 𝐷0 , 𝐷𝑤 (8.3) , 𝑓 = 0,015 – коэффициент трения, 𝐹𝑟 – реакция КПД в подшипниках: 𝜂= 𝑀−𝑀𝑡𝑟 𝑀 . (7.5) Проверка выбранных подшипников: Таблица 13 – Проверка КПД работы подшипников № вала 2 3 4 M, Нмм 67 430 3750 Тип подшипника 1000092 1000093 1000096 𝐷0 , мм 4 5,5 10,5 𝐹𝑅 , Н 11,7 68,2 59,8 𝑀0𝑎 , Нмм 0,16 0,22 0,42 𝑀𝑡𝑟 , мм 0,89 4,65 5,36 𝜂 0,987 0,989 0,999 Вид проектированного ЭМП представлен на рис. 10. Рисунок 10. Модель проектируемого ЭМП (верхняя пластина скрыта) 25 9. Проверочные расчеты 9.1 Проверочный расчет на точность Разрабатываетмая кинематика должна удовлетворять условию: ∆𝛴 ≤ [𝛿0 𝑆], (9.1) где ∆𝛴 – погрешность передачи; [𝛿0 𝑆] = 15` – заданная погрешность передачи. Погрешность передачи состоит из кинематической погрешности и погрешности мертвого хода: ∆𝛴 = ∆𝜑𝑖0𝛴 + ∆𝜑Л𝛴 (9.2) Определение этих погрешностей, в соответствии с ТЗ проводится вероятностным методом с вероятностью выхода параметра за пределы допуска 𝑝 = 0,27%. Таблица 14 – Исходные данные для проверочных расчетов № З.К. i z d, мм aω, мм m 20 8 Fr, мкм 16 22 16 26 18 30 TH, мкм 23 38 23 45 32 45 Fp, мкм ff, мкм Kφ K Ks fa, мкм EHS, мкм jnmin, мкм 22 9 30 9 1 22 9 35 9 1 22 9 42 9 1 1 2 3 5 20 8 24 0,4 0.96 0.87 ±16 132 52,8 30,4 0,4 16 20 10 180 90 50 0,5 0.98 0.99 ±20 26 9 6 9 0.98 0.99 ±16 22 9 5 6,6 100 40 16 4 18 28 11 1. Расчет кинематической погрешности Назначим степень точности 7 на все передачи. Определим вид сопряжения из условия: 𝑗𝑝 ≤ 𝑗𝑛 𝑚𝑖𝑛 , (9.3) где 𝑗𝑝 — расчётное значение бокового зазора; jn min — минимальное значение гарантированного бокового зазора для соответствующего вида сопряжения. Расчётное значение бокового зазора определяется по формуле: 𝑗𝑝 = 𝑗𝑛𝑡 + 𝑗с , (9.4) где 𝑗𝑛𝑡 — боковой зазор, компенсирующий изменение рабочей температуры; jс — боковой зазор, необходимый для размещения слоя смазки. Боковой зазор, компенсирующий изменение рабочей температуре, определяется по формуле: 𝑗𝑛𝑡 = 0,684 · 𝑎𝜔 · (𝛼зк · (𝑡зк − 20°) − 𝛼кор · (𝑡кор − 20°)), (9.5) где аω — межосевое расстояние; αзк и αкор — коэффициенты линейного расширения материалов зубчатого колеса и корпуса; tзк и tкор — температура нагрева зубчатого колеса и корпуса. Если в качестве материала корпуса использовать сталь, то значения коэффициентов линейного расширения данных материалов 𝛼зк ≈ 𝛼кор = 12 · 1 10−6 ° и температуры нагрева зубчатого колеса и корпуса также равны, тогда С 𝑗𝑛𝑡 = 0,684 · 𝑎𝜔 · 𝛼зк · (𝑡зк − 𝑡кор ) ⇒ 𝑗𝑛𝑡 = 0 мкм. Значение зазора, необходимого для размещения смазки, определяется по формуле: 𝑗с = 0,01 · 𝑚, где m — модуль зацепления. Тогда, учитывая что 𝑗𝑝 = 𝑗с: 𝑗𝑝12 = 𝑗с12 = 0,01 · 0,4 = 0,004мм; 𝑗𝑝34 = 𝑗с34 = 0,01 · 0,4 = 0,004мм; 𝑗𝑝56 = 𝑗с56 = 0,01 · 0,5 = 0,005мм. 27 (9.5) Вывод: на все передачи назначим вид сопряжения G. Минимальное значение кинематической погрешности: ′ ′ ′ ) 𝐹𝑖0𝑚𝑖𝑛 = 0,71𝐾𝑠 (𝐹𝑖1 + 𝐹𝑖2 , (9.6) ′ ′ где 𝐾𝑠 – коэффициент фазовой компенсации; 𝐹𝑖1 , 𝐹𝑖2 - допуск на кинематическую погрешность шестерни и колеса соответственно. 𝐹𝑖′ = 𝐹𝑝 + 𝑓𝑓 , (9.7) где 𝐹𝑝 – допуск на накопленноую погрешность шага зубчатого колеса; 𝑓𝑓 – допуск на погрешность профиля зуба. Максимальное значение кинематической погрешности: ′ ′ ′ ) 𝐹𝑖0𝑚𝑎𝑥 = 𝐾 · 𝐾𝜑 · (𝐹𝑖1 + 𝐹𝑖2 , (9.8) ′ ′ где K — коэффициент фазовой компенсации; 𝐹𝑖1 , 𝐹𝑖2 — допуски на кинематическую погрешность шестерни и колеса; Kφ — коэффициент учитывающий угол поворота выходного звена. Угловая погрешность элементарной передачи: 𝐹 ′ ∙180∙60 ∆𝜑𝑖0 = 𝑚𝑧𝑖02 2 ∙1000𝜋 = ′ 6,88𝐹𝑖0 𝑚𝑧2 , (9.9) ′ где 𝑚 – модуль передачи; 𝑧2 – число зубьев ведомого колеса; 𝐹𝑖0 - значение кинематической погрешности. Вероятностное значение кинематической погрешности цепи: 𝑝 2 𝑝 ∆𝜑𝑖0𝛴 = 𝐸𝑖𝛴 + 𝑡1 √∑𝑛𝑗=1(𝜉𝑗 𝑉𝑖𝑗 ) , (9.10) 𝑝 где 𝐸𝑖𝛴 – суммарная координата середины поля расеяния кинематической погрешности цепи; 𝑡1 = 0,57 – коэффициент, учитывающий процент принятого риска; 𝜉𝑗 – передаточный коэффициент элементарной передачи; 𝑉𝑖𝑗 – поле рассеяния погрешности. 28 𝑝 𝐸𝑖𝛴 = ∑𝑛𝑗=1 𝜉𝑗 𝐸𝑖𝑗 ; 𝜉𝑗 = 1 𝑖𝑗−в (9.11) , (9.12) где 𝑖𝑗−в – передаточное отношение кинематической цепи между выходными валами 𝑗-й передачи и привода. Координаты середины поля рассеяности и поле рассеяния погрешности соответственно: 𝜑 𝜑 ∆𝜑𝑖0𝑚𝑎𝑥 +∆𝜑𝑖0𝑚𝑖𝑛 ; (9.13) 𝑉𝑖𝑗 = ∆𝜑𝑖0𝑚𝑎𝑥 − ∆𝜑𝑖0𝑚𝑖𝑛 . (9.14) 𝐸𝑖𝑗 = 2 𝜑 𝜑 Произведем расчет для вех передач: ′ 𝐹𝑖1 = 22 + 9 = 31 мкм; ′ 𝐹𝑖2 = 30 + 9 = 39 мкм; ′ 𝐹𝑖3 = 22 + 9 = 31 мкм; ′ 𝐹𝑖4 = 35 + 9 = 44 мкм; ′ 𝐹𝑖5 = 22 + 9 = 31 мкм; ′ 𝐹𝑖6 = 42 + 9 = 51 мкм. Минимальное значение кинематической погрешности: ′ 𝐹𝑖0𝑚𝑖𝑛12 = 0,71 ∙ 0,87 ∙ (31 + 39) = 43,2 мкм; ′ 𝐹𝑖0𝑚𝑖𝑛34 = 0,71 ∙ 0,99 ∙ (31 + 44) = 52,7 мкм; ′ 𝐹𝑖0𝑚𝑖𝑛56 = 0,71 ∙ 0,99 ∙ (31 + 51) = 57,6 мкм. Максимальное значение кинематической погрешности: ′ 𝐹𝑖0𝑚𝑎𝑥12 = 0,96 · 1 · (31 + 39) = 67,2мкм; ′ 𝐹𝑖0𝑚𝑎𝑥34 = 0,98 · 1 · (31 + 44) = 73,5мкм; ′ 𝐹𝑖0𝑚𝑎𝑥56 = 0,98 · 1 · (31 + 51) = 80,4мкм. Угловая погрешность элементарной передачи: ∆𝜑𝑖0𝑚𝑖𝑛12 = 6,88 ∙ 43,2 = 7,43′ ; 0,4 ∙ 100 ∆𝜑𝑖0𝑚𝑖𝑛34 = 6,88 ∙ 52,7 = 6,87′ ; 0,4 ∙ 132 29 ∆𝜑𝑖0𝑚𝑖𝑛56 = 6,88 ∙ 57,6 = 4,40′ ; 0,5 ∙ 180 ∆𝜑𝑖0𝑚𝑎𝑥12 = 6,88 ∙ 67,2 = 11,56′ ; 0,4 ∙ 100 ∆𝜑𝑖0𝑚𝑎𝑥34 = 6,88 ∙ 73,5 = 9,58′ ; 0,4 ∙ 132 ∆𝜑𝑖0𝑚𝑎𝑥56 = 6,88 ∙ 80,4 = 6,15′ . 0,5 ∙ 180 Передатоные коэффициенты элементарных передач: 𝜉1 = 1 𝑖2−в 𝜉2 = = 1 1 = = 0,017; 𝑖34 ∙ 𝑖56 6,6 ∙ 9 1 𝑖3−в = 1 1 = = 0,111; 𝑖56 9 𝜉3 = 1. Координаты середины поля рассеяности: 7,43 + 11,56 = 9,5′; 2 6,87 + 9,58 𝐸𝑖2 = = 8,2′; 2 4,40 + 6,15 𝐸𝑖3 = = 5,3′ . 2 𝐸𝑖1 = Поле рассеяния погрешности: 𝑉𝑖1 = 11,56 − 7,43 = 4,1′ ; 𝑉𝑖2 = 9,58 − 6,87 = 2,7′ ; 𝑉𝑖3 = 6,15 − 4,40 = 1,75′ . Суммарная координата середины поля расеяния кинематической погрешности цепи: 𝑝 𝐸𝑖𝛴 = 0,017 ∙ 9,5 + 0,111 ∙ 8,2 + 1 ∙ 5,3 = 6,37′ . Вероятностное значение кинематической погрешности цепи: 𝑝 ∆𝜑𝑖0𝛴 = 6,37 + 0,57 √(0,017 ∙ 4,1)2 + (0,111 ∙ 2,7)2 + (1 ∙ 1,75)2 = 7,38′ . 30 2. Расчет погрешности мертвого хода Вероятностное значение кинематической погрешности цепи: 𝑝 2 𝑝 ∆л𝛴 = 𝐸л𝛴 + 𝑡2 √∑𝑛𝑗=1(𝜉𝑗 𝑉л𝑗 ) , (9.15) 𝑝 где 𝐸л𝛴 – суммарная координата середины поля расеяния люфтовой погрешности цепи; 𝑡2 = 0,46 – коэффициент, учитывающий процент принятого риска; 𝜉𝑗 – передаточный коэффициент элементарной передачи; 𝑉л𝑗 – поле рассеяния люфтового хода передачи. 𝑝 𝐸л𝛴 = ∑𝑛𝑗=1 𝜉𝑗 𝐸л𝑗 ; 𝜉𝑗 = 1 𝑖𝑗−в (9.16) , (9.17) где 𝑖𝑗−в – передаточное отношение кинематической цепи между выходными валами 𝑗-й передачи и привода. Координаты середины поля рассеяности и поле рассеяния погрешности соответственно: 𝜑 𝐸л𝑗 = 𝜑 ∆𝜑л0𝑚𝑎𝑥 +∆𝜑л0𝑚𝑖𝑛 2 𝜑 ; 𝜑 𝑉л𝑗 = ∆𝜑л0𝑚𝑎𝑥 − ∆𝜑л0𝑚𝑖𝑛 . (9.18) (9.19) Угловая погрешность элементарной передачи: ∆𝜑л = 6,88𝑗𝑡 𝑚𝑧2 , (9.20) где 𝑗𝑡 – значение мертвого хода рассчитываемаой передачи. Минимальное значение мертвого хода: 𝑗𝑡 𝑚𝑖𝑛 = 𝑗𝑛 𝑚𝑖𝑛 𝑐𝑜𝑠𝛼∙𝑐𝑜𝑠𝛽 , (9.21) где 𝑗𝑛 𝑚𝑖𝑛 – минимальное значение гарантированного бокового зазора соответствуеющей передачи; 𝛼 = 20° – угол профиля исходного контура; 𝛽 = 0 – угол налона боковой стороны профиля. Максимальное значение мертвого хода передач: 31 2 2 ) 2 2 𝑗𝑡 𝑚𝑎𝑥 = 0,7 · (𝐸𝐻𝑆1 + 𝐸𝐻𝑆2 ) + √0,5 · (𝑇𝐻1 + 𝑇𝐻2 + 2 · 𝑓𝑎2 + ∆𝑝𝑟1 + ∆𝑝𝑟2 , (9.22) где EHS — наименьшее смещение исходного контура зубчатого колеса; TH — допуск на смещение исходного контура зубчатого колеса; fa — допуск на отклонение межосевого расстояния передачи; ∆𝑝𝑟 — радиальный зазор в опорах зубчатого колеса. Произведем расчет для вех передач: 𝑗𝑡 min 1 = 9 = 9,57; cos(20) ∙ 1 𝑗𝑡 min 1 = 9 = 9,57; cos(20) ∙ 1 𝑗𝑡 min 1 = 11 = 11,7; cos(20) ∙ 1 𝑗𝑡 max 1 = 0,7 · (16 + 22) + √0,5 · (232 + 382 ) + 2 · 162 + 0 + 132 = 67,44; 𝑗𝑡 max 2 = 0,7 · (16 + 26) + √0,5 · (232 + 452 ) + 2 · 162 + 132 + 132 = 75,52; 𝑗𝑡 max 2 = 0,7 · (18 + 28) + √0,5 · (322 + 452 ) + 2 · 202 + 132 + 132 = 83,8. Угловая погрешность элементарной передачи: ∆𝜑л min 1 = 6,88 ∙ 9,57 = 1,65′; 0,4 ∙ 100 ∆𝜑л min 2 = 6,88 ∙ 9,57 = 1,25′; 0,4 ∙ 132 ∆𝜑л min 3 = 6,88 ∙ 11,7 = 0,89′ ; 0,5 ∙ 180 ∆𝜑л max 1 = 6,88 ∙ 67,44 = 11,6′; 0,4 ∙ 100 ∆𝜑л max 2 = 6,88 ∙ 75,52 = 9,84′; 0,4 ∙ 132 ∆𝜑л max 3 = 6,88 ∙ 83,8 = 6,41′ . 0,5 ∙ 180 Координаты середины поля рассеяности: 𝐸л1 = 1,65 + 11,6 = 6,63′; 2 32 1,25 + 9,84 = 5,55′; 2 0,89 + 6,41 = = 3,65′ . 2 𝐸л2 = 𝐸л3 Поле рассеяния погрешности: 𝑉л1 = 11,6 − 1,65 = 9,95′ ; 𝑉л2 = 9,84 − 1,25 = 8,59′ ; 𝑉л3 = 6,41 − 0,89 = 5,52′ . Суммарная координата середины поля расеяния кинематической погрешности цепи: 𝑝 𝐸л𝛴 = 0,017 ∙ 6,63 + 0,111 ∙ 5,55 + 1 ∙ 3,65 = 4,38′ . Вероятностное значение кинематической погрешности цепи: 𝑝 ∆л0𝛴 = 4,38 + 0,46 √(0,017 ∙ 9,95)2 + (0,111 ∙ 8,59)2 + (1 ∙ 5,52)2 = 6,96′ . Погрешность передачи: ∆𝛴 = 7,38 + 6,96 = 14,85′ , ∆𝛴 ≤ [𝛿0 𝑆] = 15′ — проверка проходит. 9.2 Проверка правильности выбора двигателя Условие правильного выбора двигателя для кратковременного режима работы отпределяется соотношением: ∗ ∗ 𝑀п ≥ 𝑀с.пр + 𝑀д.пр , (9.22) ∗ ∗ где 𝑀п = 54 Нмм – пусковой момент двигателя; 𝑀с.пр , 𝑀д.пр - соответственно уточненные статический и динамический моменты, приведенные к валу двигателя. Уточненный статический момент: ∗ 𝑀с.пр = Mн , ∗ io · 𝜂ц∗ · 𝜂под 33 (9.23) где Mн – момент нагрузки; iо – общее передаточное отношение; 𝜂ц∗ — уточненное значение КПД передач цепи двигатель-нагрузка. Уточненные значения КПД цилиндрической зубчатой передачи рассчитаем по формуле: ∗ 𝜂ц𝑖 =1− 𝜋𝑓𝐶𝜀𝜈 2 1 1 𝑧1 𝑧2 ( − ) (9.24) 𝑓 = 0,06 – коэффициент трения для матерала шестерни (сталь); εν = 1,5 – коэффициент перекрытия (для приборостроения); С – коэффициент нагрузки. 𝐶= где 𝐹 = 2 M d 𝐹+2.92 , (9.25) 𝐹+0.174 – окружная сила. При 𝐹 ≥ 30 Н принимают 𝐶 = 1. 𝐹6 = 𝐹2 = 2 ∙ 0,067 = 3,35 Н; 0,04 𝐹4 = 2 ∙ 0,43 = 16,29 Н; 0,0528 2 ∙ 3,75 = 83,33 Н > 30𝐻, значит, С6 = 1; 0.09 3,35 + 2,92 𝐶2 = = 1,78 3,35 + 0,174 𝐶4 = 16,29 + 2,92 = 1,17 16,29 + 0,174 𝜋 ∙ 0,06 ∙ 1,78 ∙ 1,5 1 1 ( + ) = 0,985 2 20 100 𝜋 ∙ 0,06 ∙ 1,17 ∙ 1,5 1 1 =1− ( + ) = 0,991 2 20 132 𝜋 ∙ 0,06 ∙ 1,00 ∙ 1,5 1 1 =1− ( + ) = 0,992 2 20 180 ∗ 𝜂пер12 =1− ∗ 𝜂пер34 ∗ 𝜂пер56 Таблица 15 – Расчет уточненного статического момента № 1-2 3-4 5-6 𝑀, Hм 0,067 0,43 3,75 𝑑зк , м 0,04 0,528 0,09 𝐹, H 𝐶 𝑧1 𝑧2 3,35 16,3 83,3 1,78 1,17 1 20 20 20 100 132 180 ∗ 𝜂ц∗ = ∏ 𝜂ц𝑖 = 0,968; 34 ∗ 𝜂ц𝑖 0,985 0,991 0,992 ∗ 𝜂под𝑖 0,987 0,989 0,999 ∗ ∗ 𝜂под = ∏ 𝜂под𝑖 = 0,975; Тогда ∗ 𝑀с.пр = 1,25 = 0,0044 Нмм. 300 · 0,968 · 0,975 Уточненный динамический момент: ∗ 𝑀д.пр = 𝐽пр ∙ 𝜀, (9.26) где 𝐽пр – приведенный к валу двигателя момент инерции всего ЭМП,кг ∙ м2 ; 𝜀 – угловое ускорение вала двигателя, рад/с2 . Угловое ускорение вала: 𝜀 = 𝜀н · io = 5 ∙ 300 = 1500 рад/с. Приведенный момент инерции: 𝐽 𝐽пр = 𝐽р + 𝐽рпр + 2н , (9.27) 𝑖0 где 𝐽р = 1,7 ∙ 10−6 кг ∙ м2 – момент инерции вращающихся частей двигателя; 𝐽рпр – приведенный момент инерции редуктора; 𝐽н = 0,5 кг ∙ м2 – момент инерции нагрузки/ Приведенный момент инерции редуктора: 𝐽рпр = 𝐽1 + 𝐽2 2 𝑖12 + ⋯+ 𝐽𝑛 2 𝑖1−𝑛 . (9.28) Рассчитаем момент инерции каждого звена по формуле: 𝐽= 𝜋𝑏𝜌𝑑 4 10−12 32 , (9.29) где 𝑏 – толщина, мм; 𝑑 – диаметр звена, мм; 𝜌 = 7,85 г/см3 – плотность матерала звеньев. 𝜋 ∙ 4,4 ∙ 7,85 ∙ 84 ∙ 10−12 𝐽1 = = 1,39 ∙ 10−8 кг ∙ м2 ; 32 𝜋 ∙ 4 ∙ 7,85 ∙ 404 ∙ 10−12 𝐽2 = = 7,89 ∙ 10−6 кг ∙ м2 ; 32 𝜋 ∙ 4,4 ∙ 7,85 ∙ 84 ∙ 10−12 𝐽3 = = 1,39 ∙ 10−8 кг ∙ м2 ; 32 35 𝜋 ∙ 4 ∙ 7,85 ∙ 52,84 ∙ 10−12 𝐽4 = = 2,396 ∙ 10−5 кг ∙ м2 ; 32 𝜋 ∙ 5,5 ∙ 7,85 ∙ 104 ∙ 10−12 𝐽5 = = 4,24 ∙ 10−8 кг ∙ м2 ; 32 𝜋 ∙ 5 ∙ 7,85 ∙ 904 ∙ 10−12 𝐽6 = = 2,53 ∙ 10−4 кг ∙ м2 . 32 Таблица 16 – Расчет уточненного динамического момента № 1 2 3 4 5 6 𝑖 5 6,6 9 𝑑зк , м 0,008 0,04 0, 008 0,0528 0,01 0,09 𝐽 ∙ 10−9 , кг ∙ м2 13,9 7892 13,9 23959 42,4 252819 𝑏, мм 4,4 4 4,4 4 5,5 5 ∗ 𝜂ц𝑖 ∗ 𝜂под𝑖 0,985 0,987 0,991 0,989 0,992 0,999 Приведенный момент инерции редуктора: 𝐽рпр = 13,9 + 7892 + 13,9 23959 + 42,4 252819 + + = 355 ∙ 10−9 кг ∙ м2 . 2 2 2 5 (5 ∙ 6,6) (5 ∙ 6,6 ∙ 9) Приведенный момент инерции: 𝐽пр = 1,7 ∙ 10−6 + 355 ∙ 10−9 + 0,5 = 7,6 ∙ 10−6 кг ∙ м2 . 2 300 Уточненный динамический момент: ∗ 𝑀д.пр = 7,6 ∙ 10−6 ∙ 1500 = 0,01142 Нм. Проверка выбранного двигателя: ∗ ∗ 𝑀с.пр + 𝑀д.пр = 0,0044 + 0,01142 = 0,0158 Нм, что меньше чем 𝑀п = 0,054 Нм, следовательно, двигатель подобран верно. 9.3 Проверочные расчеты на прочность Для открытых цилиндрических прмозубых передач должны выполняться зависимости: 𝜎Н = √ 𝑀2 𝐾𝐾𝛼3 (𝑖12 +1)3 2 𝑏𝑎2 𝑖12 36 ≤ [𝜎Н ], (9.30) где 𝑀2 – момент на колесе; 𝐾 – коэффициент расчетной нагрузки; 𝑖12 – 3 передаточное отношение ступени; 𝐾𝛼 = 0,82 √𝐸пр cos 2 𝛽 ; 𝑎 – межосевое расстояние; 𝑏 – ширина колеса. Допускаемое напряжение для шестерен и колес: [𝜎Н ] = 𝜎Н𝑅 ∙𝑍𝑅 ∙𝑍𝑉 ∙𝐾𝐻𝐿 𝑆𝐻 , (9.31) где 𝜎Н𝑅 – предел выносливости поверхности зуба; 𝑍𝑅 = 1 – коэффициент шероховатости сопряженных поверхностей; учитывающий окружную скорость колеса; 𝑍𝑉 = 1 – коэффициент, 𝑆𝐻 = 1,15 – коэффициент безопасности; 𝐾𝐻𝐿 – коэффициент долговечности. 𝑚 𝑁 𝐾𝐻𝐿 = √ 𝐻𝑂 , 𝑁 𝐻 (9.32) где 𝑚 = 6 – показатель степени для стальных колес; 𝑁𝐻𝑂 = 3 ∙ 107 – базовое число циклов для стальных улучшаемых колес; 𝑁𝐻 = 60𝑛𝑐𝐿 – расчетное число циклов нагружения, где 𝑛 – частота вращения зубчатого колеса, 𝑐 – число колес в зацеплении с расчитываемым, 𝐿 – срок службы передачи.При расчетном значении 𝐾𝐻𝐿 > 2,4, его принимают равным 2,4. 6 𝐾𝐻𝐿 = √ 3 ∙ 107 = 2,6 60 ∙ 15 ∙ 1 ∙ 100 [𝜎Н ]Ш = (2 ∙ 240 + 70) ∙ 1 ∙ 1 ∙ 2,4 = 1147,8 МПа; 1,15 [𝜎Н ]К = (2 ∙ 250 + 70) ∙ 1 ∙ 1 ∙ 2,4 = 1189,6 МПа. 1,15 К сравнению принимаем большее значение [𝜎Н ] = 1189,6 МПа. 1. Расчет на изгибную прочность: Коэффициент расчетной нагрузки: 𝐾 = 𝐾𝐹𝑉 ∙ 𝐾𝐹𝛽 , (9.33) где 𝐾𝐹𝑉 = 1,2 – коэффициент динамической нагрузки; 𝐾𝐹𝛽 = 1,17 – коэффициент неравномерности нагрузки по ширине зуба. Приведенный модуль упругости: 37 𝐸пр = 2𝐸1 𝐸2 𝐸1 +𝐸2 , (9.34) где 𝐸1 , 𝐸2 – модули упругости материалов шестерни и колеса. Так как он одинаков для обоих материалов, а зубья прямые 3 3 𝐾𝛼 = 0,82√𝐸 = 0,82 √2,1 ∙ 105 = 48. Проведем расчет для первой и последней ступени. Уточним момент на каждом валу (по табл. 16): М∗∑𝑖 = 𝑀𝑖+1 ∗ 𝑖𝑗 ·𝜂𝑗∗ ∙𝜂под𝑖 + 𝜀𝐻 𝑖𝑗 (𝐽𝑖 + 𝐽𝑖+1 ). (9.35) М𝐼𝑉 = 𝑀Н + 𝐽Н 𝜀𝐻 = 1,25 + 0,5 · 5 = 3,75 Н · м; М∗∑𝐼𝐼𝐼 = 3,75 + 5 ∙ 9 ∙ (4,24 ∙ 10−8 + 2,53 ∙ 10−4 ) = 0,436Н ∙ м; 9 · 0.992 · 0,985 М∗∑𝐼𝐼 = 0,436 + 5 ∙ 9 ∙ 6,6 ∙ (1,39 · 10−8 + 2,396 ∙ 10−5 ) = 0,075Н ∙ м; 6,6 · 0.991 · 0,989 М∗∑𝐼 = 0,075 + 5 ∙ 9 ∙ 6,6 ∙ 5 ∙ (1,38 · 10−8 + 7,89 ∙ 10−6 ) = 0,027Н ∙ м. 5 · 0.985 · 0,999 Расчитаем напряжение на первой и последней ступени: 𝜎Н1 𝜎Н5 27 ∙ 1,2 ∙ 1,17 ∙ 483 ∙ (5 + 1)3 =√ = 126 МПа; 52 ∙ 4 ∙ 242 3750 ∙ 1,2 ∙ 1,17 ∙ 483 ∙ (9 + 1)3 √ = = 758 МПа; 92 ∙ 5 ∙ 502 𝜎Н5 ≤ [𝜎Н ], проверка выполняется. 2. Проверка прочности зубьев при кратковременных нагрузках Необходимо чтобы выполнялось условие: 𝜎Н𝑚𝑎𝑥 = 𝜎Н √𝐾пер ≤ [𝜎Н ]𝑚𝑎𝑥 , (9.36) где 𝐾пер – коэффициент перегрузки, 𝜎Н – контактное напряжение, [𝜎Н ]𝑚𝑎𝑥 = 2,8𝜎т – допустимое напряжение при улучшении. [𝜎Н ]max Ш = 2,8 ∙ 360 = 1008 МПа; [𝜎Н ]max К = 2,8 ∙ 250 = 700 МПа; 𝐾пер = 𝑀пуск 0,054 = = 1,4. 𝑀 0,027 38 Тогда 𝜎Н𝑚𝑎𝑥 = 758 ∙ √1,4 = 901 МПа. 𝜎Н𝑚𝑎𝑥 ≤ [𝜎Н ]𝑚𝑎𝑥 , проверка выполняется. 39 Список литературы 1. Кокорев Ю.А., Жаров В.А., Торгов А.М. Расчет электромеханического привода. Изд-во МГТУ, 1995, 132 с. 2. Буцев А.А., Еремеев А.И., Кокорев Ю.А. и др. Атлас конструкций ЭМП. Под ред. Тищенко О.Ф. Машиностроение, 1982. 3. Буцев А.А. Электроэлементы в конструкции приборов: Справочное пособие по курсу «Основы конструирования приборов» / Под ред. В.Н. Баранова. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2000. – 27с., ил.