Гибкое программирование Sinumerik

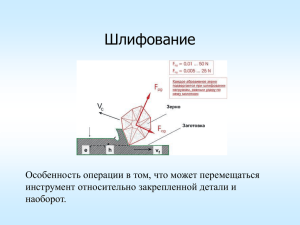
Г. ГРОМОВ
Гибкое программирование для станков с ЧПУ
в среде Sinumerik-840D
Для средних технических учебных заведений
г. Александров
2014
Громов Г.С.
Гибкое программирование для станков с ЧПУ в среде Sinumerik-840D
Aлександровский промышленно-гуманитарный колледж,
факультет «Технология машиностроения», Владимирская область
Гибкое программирование – что это такое?
Как облегчить труд программиста-технолога?
Об этом в этой книжке.
© Громов Г.С., 2014
2
Моему первому станку
с системой ЧПУ «Контур-2ПТ»
посвящается
От автора:
В состав современного оборудования с программным управлением входят мощные
средства программирования, которые наряду с классическими схемами, предоставляют
пользователю ряд широких возможностей по созданию универсальных компактных
программ. Как только в составе устройств с ЧПУ появилась ЭВМ (в нашей стране незабвенная «Электроника-60») программирование приобрело совершенно иной вид. Вместо
последовательного считывания и дальнейшей отработки кадра появилась возможность
со стороны программиста воздействовать на ход выполнения программы: осуществлять
переходы по условию и без, изменять координаты начальной точки, производить
отработку зеркально относительно осей и т. п. Тогда же появилось и понятие параметра,
а вместе с ним появление понятия «программирования с параметрами» или параметрического программирования. Казалось бы, твори, выдумывай. Но не тут-то было. Эксплуатационная документация по этому вопросу оказалась настолько невнятной, что новые
возможности практически не использовались. В данной книге я попытался исправить
это недоразумение. Полагаю, что некоторые читатели подумают про козу и баян, мол,
для чего всѐ? Вон создал модель, пропустил через САМ-систему и получи программу.
Согласен. Для обработки сложных поверхностей так и поступают. Но бывают моменты,
когда такие действия не целесообразны. Для обработки некоторых деталей САМ-система
выдаст программу объѐмом в несколько мегабайт, в то же время нужный результат
можно получить, написав программу лишь в несколько десятков кадров. Изменятся
начальные данные - снова модель и т.д. В программе с параметрами достаточно будет
лишь заменить пару данных. Впрочем, не буду навязывать своего мнения, читатель
разберѐтся.
Эту книгу я написал для студентов нашего колледжа, которые осваивают
специальность техник-технолог-программист, отрабатывая навыки на токарном
и фрезерном станках с УЧПУ Sinumerik-840D. Надеюсь, конечно, что ею заинтересуются и другие соответствующие учебные заведения. Тогда, быть может, мы и удвоим
ВВП, что нам обещал другой ВВП к 2010 году.
Успехов Вам!
Г. Громов
P.S. Почти все примеры, приведенные в книге, были реализованы на токарном и
и фрезерном станках EMCO Concept Turn & Mill 155A студентами колледжа
на практических занятиях.
3
Содержание
Начальные установки и соглашения …………………………………………………..6
1.
Фреймы ……………………………………………………………………..8
1.1.
1.2.
1.3.
1.4.
1.5.
1.6.
1.7.
Параметры ………………………………………………………………………...8
Счѐтный цикл FOR ……………………………………………………………….8
Сдвиг системы координат, TRANS, ATRANS ………………………………...11
Программируемое зеркальное отображение, MIRROR, AMIRROR ………...14
Программируемый поворот, ROT, AROT ……………………………………..18
Программируемое изменение масштаба, SCALE, ASCALE………………….23
Заключение к разделу 1 …………………………………………………………26
2.
Подпрограммы …………………………………………………………………...31
2.1.
2.2.
2.3.
2.4.
2.5.
Общая информация ……………………………………………………………..31
Подпрограммы, составленные в относительной системе отсчѐта ……………32
Подпрограммы, составленные в абсолютной системе отсчѐта ……………….38
Подпрограммы с параметрами R ………………………………………………..41
Подпрограммы с передачей параметров ………………………………………..43
3.
Гибкое программирование (теория) …………………………………………….46
3.1. Переменные ……………………………………………………………………...46
3.2. Функции вычисления …………………………………………………………. 47
3.3. Безусловные программируемые переходы …….…………………………….. 48
3.4. Операторы сравнения и логические переходы ………………………………..49
3.5. Приоритет операций …………………………………………………………… 50
3.6. Ветвление программы. Оператор CASE…OF…DEFAULT…………………..51
3.7. Управляющие структуры ……………………………………………………….53
3.7.1. Программный цикл с альтернативой ( IF …, ELSE …, ENDIF) ……………..53
3.7.2. Счѐтный цикл ( FOR … TO …, ENDFOR) …………………………………...53
3.7.3. Бесконечный программный цикл ( LOOP, ENDLOOP) ……………………...54
3.7.4. Программный цикл с условием в начале цикла ( WHILE, ENDWHILE) …...54
3.7.5. Программный цикл с условием в конце цикла ( REPEAT, UNTIL) ………...55
3.8. Подавление отображения текущего кадра ( DISPLOF, DISPLON) …………56
4.
Гибкое программирование (примеры) ………………………………………..57
4.1. Программирование нелинейных фигур на плоскости XOY (G17) ……….…57
4.1.1 Тригонометрическая функция Y=SIN(X) ……………………………………..57
4.1.2. График функции Y=SIN(X)/X ……………………………………………...…59
4.1.3. Эллипс …………………………………………………………………………...61
4.2. Параболоид …………………………………………………………………..….64
4.3. Программирование цилиндрической резьбы, профиль которой
изменяется по косинусоидальному закону ………………………………..…..66
.
4
4.4.
Программирование конической резьбы, профиль которой
изменяется по косинусоидальному закону ……………………………………68
4.5. Программирование цилиндрической «верѐвочной» резьбы …..
4.6.
Программирование скосов ……………………………………………………...72
4.7.
4.8.
4.9.
4.10.
4.11.
4.12.
Конические поверхности ……………………………………………………….75
Цилиндрические поверхности …………………………………………………77
Сферические поверхности ……………………………………………………...80
Вогнутые цилиндрические поверхности ………………………………….......82
Вогнутые сферические поверхности …………………………………………..84
Программирование объѐмных фигур с одновременным
движением по трѐм осям ………………………………………………………..86
5.
Примеры разработки универсальных подпрограмм …………………………..88
5.1. Подпрограмма растачивания отверстий различного диаметра
и глубины фрезой произвольного диаметра ……………………………………88
5.2. Подпрограмма для фрезерования правильных пирамид ………………………91
5.3. Подпрограмма фрезерования полу- и части (меньшей) сферы ……………….95
Заключение ……………………………………………………………………………..98
Приложения …………………………………………………………………………….99
Литература …………………………………………………………………………….108
5
Начальные установки и соглашения
Прежде чем начать, необходимо установить некоторые соглашения.
1. Читатель должен знать основы программирования. Необязательно системы Sinumerik.
Сделав потом соответствующие замены, можно получить программы для
любых систем.
2. Желательно иметь на компьютере установленную систему WinNC Sinumerik 840D
со средствами трехмерного моделирования 3DView. Это исключительно для того,
чтобы посмотреть результаты без отработки на станке.
3. Для описания заготовки при фрезерной обработке будем применять следующие
обозначения:
число1-Х-число2 - размеры по оси Х,
число3-Y-число4 - размеры по оси Y,
Z1= толщина детали, Z2= вылет из зажимного приспособления.
Все размеры в миллиметрах. Например, заготовка с такими параметрами
10 – Х – 120, 5 – Y– 100, Z1=50, Z2=52 будет иметь вид (рис. 1):
Рис.1
6
Размеры по осям X200, Y100, Z100 до точки W – это смещения нуля детали
от нуля станка. Они должны быть записаны в функцию G54 (раздел
<ПАРАМЕТРЫ><СНТ>).
Для токарной обработки обозначения следующие (рис 1.1):
W =50 – вылет заготовки из зажимного приспособления;
D=25 – диаметр заготовки.
Ноль по оси Z всегда на торце заготовки.
Рис 1.1
4. Если обработка ведѐтся фрезой, желательно в окно РАДИУС
(раздел <ПАРАМЕТРЫ><КОРРЕКЦИЯ ИНСТРУМЕНТА> ввести еѐ радиус.
5. Фрезы, описанные в системе, имеют режущую часть в 45 мм. Поэтому при отработке
программ на станке, если нет инструмента с такими параметрами, провести предварительную обработку.
6. Режимы резания постоянны. Обороты шпинделя S1000, подача для фрезерной
обработки F100, для токарной F0.1. При отработке программ на станках необходимо
поставить реальные данные.
7. Если по ходу дела встретится аббревиатура УП, то это управляющая программа.
8. При движении фрезы в заготовку вдоль оси Z предполагается наличие в этом месте
технологического отверстия соответствующего диаметра.
7
1. ФРЕЙМЫ
Фреймы – это действия с осями координат, такие как: зеркальное отображение,
повороты на определенный градус, смена начала координат, масштабирование.
Но для начала, чтобы полностью использовать эти возможности, познакомимся
с понятием «Параметра» и циклом FOR.
1.1. ПАРАМЕТРЫ
Система Sinumerik предлагает три типа переменных: это системные переменные,
переменные пользователя и арифметические параметры. Мы остановимся на переменных,
определяемых пользователем. Это переменные различных типов, таких как: целые,
вещественные, логические, строковые, массивы и предопределенные. Пока будем
использовать последние. Переменные других типов рассмотрим позже.
Системой зарезервировано сто предопределенных переменных.
Они обозначаются латинской буквой R и индексом от 0 до 99. Диапазон
принимаемых значений в десятичном виде ±(0,0000001….99999999). Значения
R-параметрам присваиваются предварительно или по ходу выполнения программы.
С ними можно производить различные математические действия, о которых немного
позже. Также предварительные установки можно вводить в раздел <ПАРАМЕТРЫ>
<ПАРАМЕТРЫ>.
Пример.
R0=1
; параметру с индексом 0 присвоено значение 1
R4=3.14 ; параметру с индексом 4 присвоено значение 3.14
1.2. СЧЕТНЫЙ ЦИКЛ FOR
Если какой либо участок программы нужно повторить некоторое количество раз,
применяется цикл FOR.
Синтаксис:
FOR <переменная> = <начальное значение> ТО <конечное значение>
<фрагмент программы>
ENDFOR
Значения:
FOR
начало цикла
начальное значение должно быть меньше конечного
ENDFOR окончание цикла
ТО
количество повторений
Цикл обеспечивает до восьми вложений.
Пример 1.
Пример 2.
FOR R1=1 TO 10 ; повторить 10 раз
….
….
ENDFOR
FOR R1=1 TO 2
; пример 3-х уровнего вложения
8
….
FOR R2=1 TO 3
….
FOR R3=1 TO 4
…
…
ENDFOR
ENDFOR
ENDFOR
Выполнение циклов от внутреннего к внешним.
Практический пример. Растачивание матрицы отверстий. Рис. 2
Рис. 2
На этом примере покажем как с помощью оператора FOR легко программировать
обработку регулярных объектов. Во внутреннем цикле с параметром R2 программируется
непосредственная обработка отверстия за 4 прохода. Изменяя значения параметров R3 и
R1 можно обрабатывать регулярные матрицы с любым количеством отверстий, изменяя
в кадре N1 координаты Х и Y на соответствующие значения.
9
;
ОБРАБОТКА МАТРИЦЫ ОТВЕРСТИЙ
;
заготовка 0 - X - 230, 0 - Y- 140 , Z1=20,Z2=15
;
T1 - фреза D=10 MM
T1 D1 M6
M3 S1000 F100
G54 G0 X30 Y30
Z1
G1 Z0
FOR R3=1 TO 5
; горизонтальный ряд 5 отверстий
FOR R1=1 TO 3
; вертикальный ряд 3 отверстия
FOR R2=1 TO 4
; растачивание отверстия за 4 прохода
G91 Z-5.1
; глубина 1 прохода
G41 Y-14
G3 J14
G40 G1 Y14
ENDFOR
G90 Z1
G91 Y40
G90 Z0
ENDFOR
G90 Z1
N1 G91 X40 Y-120
G90 Z0
ENDFOR
G90 G0 Z50 M5
M30
Результат отработки программы представлен на рис. 3.
Рис. 3
10
1.3. Сдвиг системы координат: TRANS, ATRANS
Данная команда позволяет смещать начальную точку детали в место, удобное
для расчѐта координат опорных точек контура.
Синтаксис:
TRANS/ATRANS X±… Y±… Z±…
TRANS - абсолютный сдвиг относительно фактического нуля, занесѐнного
в G54-G599. Удаляет все предварительно запрограммированные
фреймы: TRANS, ATRANS, ROT, AROT, SCALE, ASCALE,
MIRROR, AMIRROR. TRANS без параметров возвращает всѐ
в исходное состояние.
ATRANS – относительный сдвиг относительно абсолютного (G54-G599) или
текущего нуля. Все ранее установленные фреймы сохраняются.
X, Y, Z - координаты осей, в которые устанавливается новый ноль.
Пример.
Рис. 4
На рисунке 4 представлен абсолютный сдвиг в точку X50 Y75, и относительный
сдвиг X100 Y20 (X150-X50=X100, Y95-Y75=Y20). Ниже представлена УП.
11
; Пример абсолютного и относительного сдвига нуля
; заготовка 0 - X - 200,0 -Y- 150, Z1=2, Z2=10
;
T1- фреза 10 мм
;
T1 D1 M6
M3 S1000 F100
G54 G0 X0 Y0 Z1
; абсолютный сдвиг для упрощения расчёта координат отверстий
TRANS X50 Y75
G1 X40 Y0
Z-3
Z1
X28.3 Y28.3
Z-3
Z1
X0 Y40
Z-3
Z1
X-28.3 Y28.3
Z-3
Z1
X-40 Y0
Z-3
Z1
X-28.3 Y-28.3
Z-3
Z1
X0 Y-40
Z-3
Z1
X28.3 Y-28.3
Z-3
Z1
;
относительный сдвиг
ATRANS X100 Y20
X0 Y40
Z-3
G3 X-40 Y0 CR=40
G1 Z1
X0 Y-40
Z-3
G3 X40 Y0 CR=40
G1 Z1
G0 Z50 M5
M30
12
Результат выполнения УП представлен на рисунке 5.
Рис. 5
13
1.4. Программируемое зеркальное отображение: MIRROR, AMIRROR
По командам MIRROR/AMIRROR осуществляется зеркальное отображение
относительно какой-либо оси.
Синтаксис:
MIRROR/AMIRROR X… Y… Z…
При зеркальном отражении контура движение по окружности G2/G3 и коррекция на
радиус инструмента G41/G42 изменяются автоматически.
MIRROR - абсолютное зеркальное отражение относительно абсолютного нуля,
устанавливаемого в функциях G54 – G57, G500 - G599.
MIRROR удаляет все предварительно запрограммированные фреймы.
Программирование MIRROR без адреса оси отменяет зеркальное отражение
и все другие фреймы, устанавливая всѐ в исходное состояние.
AMIRROR - относительное зеркальное отражение относительно текущих фреймов
или абсолютного смещения нуля.
X, Y, Z
-
геометрические оси для зеркального отражения.
Для иллюстрации выше сказанного приведем два примера.
Пример 1. На рисунке 6 представлено упрощенное изображение бабочки.
Рис. 6
Не ставлю здесь дополнительных размеров, для определения координат опорных
точек контура. Просто примите на веру. Далее следует текст УП. Нас в первую очередь
интересует программирование зеркального отражения.
14
; программирование зеркальной отработки
; заготовка 0-X-120, 0-Y-100, Z1=1, Z2=10
T1 D1 M6
; шпоночная фреза 10 мм
M3 S1000 F100
G0 G54 X0 Y0
Z1
TRANS X60 Y40
;смена координат начальной точки
X0 Y0
FOR R1=1 TO 2
;1 проход - правая сторона
G1 Z-1
G2 X50 Y50 CR=50
G3 X25 Y10 CR=70
G2 X15 Y0 CR=10
G1 X0
Y-15
G3 X15 Y0 CR=-15
G1 X0
AMIRROR X0
; зеркально относительно новой оси Y
; текущие значения фреймов сохраняются
; второй проход в зеркальном отображении
ENDFOR
MIRROR
; сброс всех фреймов, возврат в исходное состояние
G0 Z50 M5
X150 Y100
M30
Результат отработки программы на рисунке 7.
Рис. 7
15
Пример 2. На детали, представленной на рис. 8, необходимо прорезать 8 элементов,
четыре из которых зеркальны четырем другим.
Рис. 8
Вариантов УП здесь масса. Главное – минимальное количество кадров.
В представленном варианте: сдвиг координат в точку X100 Y0, во внутреннем цикле –
1 проход обработка правого элемента, второй проход – зеркальная обработка относительно новой оси Y.
Внешний цикл – повторение первого 4 раза с относительным сдвигом относительного
нового нуля детали.
; заготовка 0-X-200,0-Y-160, Z1=4, Z2=10
T6 D1 M6
M3 S1000 F100
G0 G54 X0 Y0
Z1
TRANS X100 Y0
FOR R2=1 TO 4
FOR R1=1 TO 2
X45.5 Y30
G1 Z-5
G2 Y50 CR=-15
G1 X70
Y47
X90
Y33
X70
Y30
X45.5
Z1
; шаровая фреза 2 мм
; сдвиг нуля
; внутренний цикл
; обработка правого элемента
16
AMIRROR X0
ENDFOR
ATRANS X0 Y32
ENDFOR
G0 Z50 M5
M30
; относительное зеркальное отражение
; относительный сдвиг нуля
Результат отработки УП на рисунке 9.
Рис. 9
17
1.5. Программируемый поворот ROT, AROT
Программируемый поворот ROT/AROT, используется для вращения системы
координат детали вокруг каждой из геометрических осей X, Y, Z на любой угол в
выбранной рабочей плоскости. В рабочей плоскости G17 поворот осуществляется
вокруг оси Z, в G18 вокруг оси Y, в G19 вокруг оси X. Будем рассматривать рабочую
плоскость XOY (G17).
Синтаксис:
ROT/AROT Z…
ROT/AROT RPL=<± значение угла>
ROT – абсолютное вращение вокруг абсолютного нуля, занесенного
в функции G54-G57, G500-G599. ROT удаляет все предшествующие фреймы
AROT – относительное вращение вокруг абсолютного нуля или относительного,
программируемого фреймами TRANS/ATRANS. Все предшествующие
фреймы сохраняются.
Z< ± градус > - ось, вокруг которой выполняется вращение
RPL=< ± градус > - поворот на заданный градус в рабочей плоскости. Градусы даются
в десятичном представлении. Например, 10º30΄ соответствует 10.5º.
Нулевой угол – ось Х в абсолютной или относительных системах координат
Положительное направление угла в рабочей плоскости G17 от оси X против движения
часовой стрелки, отрицательное – в направлении движения.
Например,
ROT Z28
; абсолютный поворот осей системы координат XOY на 28º
….
ROT RPL=30 ; абсолютный поворот на 30º
AROT RPL=-5 ; относительный поворот на -5º
; результирующий угол поворота составляет 25º
….
18
Примеры программирования с конструкцией ROT/AROT.
Пример 1. На рисунке 10 представлен эскиз детали.
Рис. 10
В центре заготовки 200х200 мм на окружности диаметром 100 мм равномерно
расположены 16 отверстий произвольного (разумного) диаметра с углом начального
смещения 5º. Программировать напрямую такую обработку слишком хлопотно. Покажем,
как с помощью команд поворота, не напрягаясь, запрограммировать обработку этой
детали. Ниже приведен текст УП. Чтобы увидеть начальный поворот в 5º, предварительно
шаровой фрезой прочертим исходные оси.
; заготовка 0-X-200, 0-Y-200, Z1=1, Z2=10
T6 D1 M6
M3 S1000 F100
G0 G54 X0 Y100 Z1
G1 Z-0.2
X200
Z1
G0 X100 Y0
G1 Z-0.2
Y200
G0 Z50 M5
; шаровая фреза 2 мм, прорисовка осей
; по центру заготовки
T2 D1 M6
M3 S1000 F100
G0 G54 X0 Y0 Z1
; сверло 6 мм
19
TRANS X100 Y100
ROT RPL=5
FOR R1=1 TO 16
X50 Y0
G1 Z-5
Z1
AROT RPL=22.5
ENDFOR
G0 Z50 M5
X200
M30
; перенос нуля в центр заготовки
; абсолютный поворот осей на 5 градусов
; сверление 16-ти отверстий в цикле
; с относительным поворотом на 22,5 градуса
Как видим, сама программа обработки составляет всего 14 кадров. На рисунке 11
представлен результат.
Рис. 11
Пример 2. На рисунке 12 представлены четыре крестика, центры которых
центрально симметричны относительно центра детали с углом наклона 30º. Был бы
этот угол 45º проблем бы не было. Повернул четыре раза на 90º и всѐ. Можно, конечно,
запрограммировать напрямую, благо, что расчеты координат опорных точек не сложные.
Но лучше всѐ сделать элегантно. Ниже показан один из вариантов программирования.
Предварительно в программе прорисованы оси, чтобы оценить правильность обработки.
Также использованы фреймы, разобранные на предыдущих стадиях.
20
Рис. 12
Текст УП.
; заготовка 0-X-200, 0-Y-160, Z1=1, Z2=10
T6 D1 M6
; фреза шаровая 2 мм, прорисовка осей
M3 S1000 F100
G0 G54 X100 Y0 Z1
G1 Z-0.4
Y160
Z1
X0 Y80
Z-0.4
X200
G0 Z50 M5
T1 D1 M6
M3 S1000 F100
G0 G54 X0 Y0 Z1
R2=0
TRANS X100 Y80
X0 Y0
FOR R1=1 TO 4
ATRANS X40 Y40
AROT RPL=30
X0 Y0
G1 Z-2
X-20
X20
X0
Y20
; фреза 10 мм
; угол
; перенос нуля
; отраБотка в цикле
; относительный сдвиг нуля в центр креста
; относительный поворот осей на 30 град.
; фрезерование креста
21
Y-20
Y0
Z1
TRANS X100 Y80
R2=R2+90
AROT RPL=R2
ENDFOR
G0 Z50 M5
X200 Y160
M30
; возврат в ноль
; увеличение угла в R2 на 90 град.
; поворот на 90 град
; конец цикла
Результат на рисунке 13.
Рис. 13
Можно сделать УП ещѐ элегантней, запрограммировав для получения крестика
один луч и повернув его четыре раза. Предоставляю это читателю.
22
1.6. Программируемое изменение масштаба: SCALE, ASCALE.
SCALE/ASCALE позволяет установить отдельные масштабные коэффициенты
для каждой оси X, Y, Z.
Синтаксис: SCALE/ASCALE X… Y… Z…
Если после SCALE/ASCALE программируется сдвиг нуля с ATRANS, он также
масштабируется.
SCALE – абсолютный масштаб относительно сдвига нуля, устанавливаемого в функциях
G54-G57, G500-G599. Удаляет все предшествующие фреймы. Программирование
SCALE без параметров отменяет все масштабные коэффициенты и возвращает
всѐ в исходное состояние.
ASCALE - относительный масштаб относительно абсолютного или текущего нуля. Все
текущие фреймы сохраняются.
X, Y, Z – масштабные коэффициенты для каждой оси. Принимает целые или дробные
значения большие нуля. Если коэффициент равен единице, соответствующий
адрес опускается.
Например,
SCALE X1.5 Y0.8 Z0.5
; значения всех последующих адресов в УП
; X, Y, Z умножаются на соответствующие
; коэффициенты.
В своей практике при разработке УП мне довелось использовать эту возможность
программирования только один раз: при создании библиотеки подпрограмм для гравирования буквенно-цифровых символов. Устанавливая коэффициенты масштабирования
по осям X и Y, можно добиться требуемых размеров символов. И еще при художественном фрезеровании (например, после обкатки САМ-системой ArtCAM), когда есть
готовая УП, но размеры заготовки больше или меньше размеров, установленных
в программе. Тогда, установив соответствующие коэффициенты для осей, можно
вписать готовую УП в свою заготовку. Но, если коэффициенты при осях X и Y
будут не одинаковы, возможно искажение общей картины.
Тем не менее, приведем пару примеров.
Пример 1. Если будете пробовать, просто перепишите эту УП.
;заготовка: -19 -X- 100, 10 -Y-25,Z1=35, Z2=40
T10 D1 M6
; фреза дисковая 35 мм
M3 S1000 F200
G0 G54 X0 Y0 Z0
G1 Z-1
FOR R1=1 TO 30
; 30 проходов со смещением по Z на -1 мм,
G90 G42 X20
; поворотом на каждом проходе 0.25 градуса
G3 X35.089 Y-8.606 I10
; и увеличением адреса Х в 1.0015 раз
G2 X88.125 Y-4.625 CR=60
G3 X92.678 Y4.156 CR=-5
X25.867 Y9.105 CR=70
23
X20 Y0 I=AC(30) J=AC(0)
G1 G40 X0
AROT RPL=0.25
ASCALE X1.0015
G91 Z-1
ENDFOR
SCALE
; сброс всех фреймов
G0 X0
G0 Z150 M5
M30
Результат на рисунке 14.
Рис. 14
Пример 2. Логарифмическая спираль
Текст УП
; логарифмическая спираль
; заготовка 100-X-100, 100-Y-100, Z1=2, Z2=3
T6 D1 M6
; шаровая фреза 2 мм
M3 S1000 F100
G0 G54 X1 Y0 Z1
G1 Z-0.2
FOR R1=1 TO 200
; 200 раз через 5 градусов
X1
AROT RPL=5
ASCALE X1.02
; масштабирование
ENDFOR
M30
24
Результат отработки УП на рисунке 15.
Рис. 15
25
1.7. Заключение к разделу 1
В заключение к первому разделу рассмотрим два примера по применению
фреймов на конкретных примерах.
Пример 1. Деталь представлена на рисунке 16.
Координаты опорных точек первого окна
1
X23.92
Y2
3
X28.25
Y25.42
2
X18.33
Y15.5
4
X37.95
Y2
Рис. 16
26
Заготовка представляет цилиндрическую шайбу диаметром 100 мм с центральным
внутренним отверстием со шпоночным пазом. Деталь имеет 8 сквозных окон плюс
18 зубьев, которые повернуты на начальный угол α, который пусть будет равен 5º20΄48˝.
Требуется составить наиболее короткую УП. Координаты опорных точек первого окна
представлены в таблице. Угол α в десятичном виде будет равен α=5,347º. Программы
могут быть разными, сколько программистов, столько и вариантов. Один из них имеет
следующий вид. В УП для наглядности прорисованы оси. В местах захода фрезы Ø8 мм
в заготовку надо было бы запрограммировать сверление технологических отверстий,
но, чтобы не загромождать УП, автор этого делать не стал.
; заготовка 50-X-50, 50-Y-50, Z1=10 Z2=15
T6 D1 M6
; шаровая фреза 2 мм
; прорисовка осей
M3 S1000 F100
G0 G54 X-55 Y0
Z-0.2
G1 X55
G0 Z2
X0 Y55
Z-0.2
G1 Y-50
G0 Z50 M5
T3 D1 M6
M3 S1000 F100
G0 G54 X60 Y0 Z1
G1 Z-11
G42 X50
G3 I-50
G0 G40 X60
ROT RPL=5.347
FOR R1=1 TO 18
X60 Y0
G1 X49
X60
AROT RPL=20
ENDFOR
ROT
G0 Z50 M5
T9 D1 M6
M3 S1000 F100
G0 G54 X0 Y0
Z1
; фреза 12 мм, зубья
; фреза 8 мм, окна
FOR R1=1 TO 8
X28 Y8
G1 Z-11
27
G42 Y2
X23.92
G3 X18.33 Y15.5 CR=24
G1 X28.25 Y25.42
G2 X37.95 Y2 CR=38
G1 X28
G40 Y10
Z1
AROT RPL=45
ENDFOR
G0 Z50 M5
X100
M30
Результат на рисунке 17.
Рис. 17
28
Пример 2. Применяя различные фреймы, составить наиболее короткую УП для детали,
представленной на рис. 18. Требуется вырезать заштрихованные участки.
В этом примере применяются все фреймы.
Рис. 18
Один из вариантов УП имеет следующий вид:
; заготовка 55-X-55, 60-Y-60, Z1=2, Z2=10
T6 D1 M6
M3 S1000 F100
G0 G54 X-55 Y0 Z1
G1 Z-0.1
X55
Z1
X0 Y60
Z-0.1
Y-60
Z1
; шаровая фреза 2 мм
; прорисовка осей
; начало обработки
29
FOR R3=1 TO 2
FOR R2=1 TO 2
FOR R1=1 TO 2
X-25 Y-27.5
Z-3
Y-5
X-20
Y-22.5 RND=5
X-5
Y-27.5
X-25
Z1
ASCALE X2 Y2
ATRANS X2.5 Y2.5
ENDFOR
TRANS
AMIRROR X0
ENDFOR
MIRROR Y0
; нижняя половина
; левый нижний фрагмент
; увеличение в 2 раза
; локальный сдвиг
; сброс всех фреймов, возврат в исходный ноль
; локальная зеркальность относительно оси Y
; нижняя половина готова
; зеркальное отражение нижней половины
; относительно абсолютной оси Х
ENDFOR
G0 Z50 M5
M30
Результат на рисунке 19.
Рис. 19
Читатель может попробовать другой алгоритм программирования.
В час добрый.
30
2. ПОДПРОГРАММЫ
2.1. Общая информация
Если при обработке деталей встречаются некие одинаковые участки, то
обработку этих участков можно выделить в отдельные программы, которые можно
будет вызывать из основной программы. Такие программы называются подпрограммами.
В настоящий момент жесткого разделения между программами и подпрограммами
нет. Просто есть главная программа, а всѐ, что из неѐ вызывается, называют подпрограммами. В свою очередь и главная программа может быть для какой-то программы
подпрограммой.
Как и во всех высокоуровневых языках программирования, так и в языке ЧПУ
подпрограммы используются для того, чтобы поместить многократно используемые
программные блоки в самостоятельные, завершенные программы.
Преимуществами подпрограмм являются:
- улучшение наглядности и читабельности программ;
- улучшение качества через повторное использование протестированных блоков
программ;
- создание специальных библиотек подпрограмм для общего доступа.
При наименовании подпрограмм следует придерживаться следующих правил:
- первыми двумя символами должны быть две буквы латинского алфавита A-Z
- последующими символами может быть любая комбинация букв и цифр (0-9) и
символа подчеркивания “_”
- максимально можно использовать 31 символ.
Расширение файла подпрограммы .SPF
Заканчиваться подпрограмма должна кодом М17.
Из подпрограммы в свою очередь также может вызываться подпрограмма,
из этой следующая и т.д. Таким образом, процессы вложены друг в друга. Каждая
подпрограмма выполняется на своѐм уровне. Глубина вложенности составляет
16 уровней. Главная программа всегда выполняется на 0 уровне, а подпрограммы
на следующих 15 по мере их появления.
Вызов подпрограмм осуществляется по их имени. Желательно, чтобы имена
главной программы и подпрограммы не были идентичны.
Например, подпрограмма обработки повторяющегося участка имеет имя MUMU.SPF.
Чтобы еѐ вызвать, просто в нужном месте надо вставить отдельный кадр MUMU.
Существует также многократный вызов подпрограмм. Его синтаксис:
MCALL MUMU ; многократный вызов подпрограммы MUMU
….
; вызов MUMU в конце движения
….
; вызов MUMU в конце движения
MCALL
; отмена
….
Ниже будут приведены примеры применения различных подпрограмм
как для фрезерной обработки, так и для токарной.
31
2.2. Подпрограммы, составленные в относительной системе отсчѐта
Такие подпрограммы можно использовать в любом месте обработки. Главное,
чтобы в подпрограмме алгебраическая сумма всех адресных значений для всех осей
была равна нулю.
Рассмотрим по паре примеров для фрезерной и токарной обработок.
Пример 1. Создадим библиотеку подпрограмм для гравирования нескольких
символов, например, для букв O, Z, R, и попытаемся отгравировать их, используя
различные коэффициенты масштабирования.
Все вы видели магазинные чеки. Если присмотреться, то можно увидеть, что
буквы и цифры на них прорисованы в виде точек. Это их пробили через красящую
ленту иголки печатающей головки, которые собраны в определѐнную матрицу.
Мы поступим таким же образом. На рис. 20 на сетке 7×5 линий нарисована буква Z.
Пусть размер одной клетки будет 1×1 мм.
Рис. 20
За начало отсчета принимается левый нижний угол, и подпрограмма составляется
в относительной системе отсчѐта. Текст еѐ выглядит следующим образом:
; подпрограмма ZZ.SPF
;
Буква Z
G1 G91
Y6
; левый верхний угол
Z-1.2
; врезание
X4
X-4 Y-6
X4
Z1.2
; подъём
X1
; переход на начало следующей буквы
G90
; возврат в абс. систему отсчёта
M17
Аналогичным образом составляются подпрограммы на символы O и R, а также на
любые другие. Главная программа, из которой вызываются наши подпрограммы
имеет вид:
32
; надпись
; заготовка 0-X-100, 0-Y-100, Z1=2, Z2=10
T6 D1 M6
;шаровая фреза 2 мм
M3 S1000 F100
G0 G54 X20 Y10
Z1
ZZ
; вызов подпрограммы для буквыZ
OO
;O
RR
;R
RR
;R
OO
;O
G0 X20 Y20
; выход в новую точку
SCALE X2 Y2 ; масштабирование
ZZ
OO
RR
RR
OO
SCALE
; сброс,
; иначе координаты точки X20 Y40 будут искажены
G0 X20 Y40
; выход в точку
SCALE X2.2 Y1.5
ZZ
OO
RR
RR
OO
G0 Z50 M5
M30
Что получилось, смотрим на рисунке 21.
Рис. 21
33
Как мы видели в разделе 1, если одинаковые участки обработки образуют
регулярную структуру, то вполне возможно использовать цикл FOR. Но, если эти
одинаковые участки расположены хаотично, то здесь без применения подпрограмм
не обойтись. Рассмотрим следующий пример.
Пример 2. На детали толщиной 15 мм ( см. рис. 22) расположены сквозные окна
в произвольной последовательности.
Рис. 22
Требуется разработать УП для изготовления этой детали.
Видим, что размеры окон одинаковые, но расположены окна как попало, обработку
в цикл FOR вставить не удастся. Значит, составляем подпрограмму в относительной
системе отсчѐта на растачивание окон за три прохода. Начальная точка – середина окна.
Назовѐм подпрограмму FENSTER.SPF ( это окно на немецком языке).
Текст подпрограммы:
;
подпрограмма FENSTER.SPF
G1 G91
FOR R0=1 TO 3
; 3 прохода
Z-5.5
G42 Y7.5
X15
Y-20
X-30
Y20
X15
G40
Y-7.5
ENDFOR
34
G90 Z1
M17
; возврат в абс. систему отсчёта
Текст главной программы:
; заготовка 0-X-200, 0-Y-160, Z1=15, Z2=10
T1 D1 M6
; фреза 10 мм
M3 S1000 F100
G54 G0 X35 Y30
Z1
MCALL FENSTER
; многократный вызов подпрограммы
G0 X35 Y30
; 1 окно
G0 X90 Y40
; 2 окно
G0 X150 Y25
; 3 окно
MCALL
G0 X145 Y115
; 4 окно с поворотом на 90 град
ROT RPL=90
FENSTER
; вызов подпрограммы
ROT
; сброс
G0 X50 Y108
; 5 окно с поворотом на 45 град
ROT RPL=45
FENSTER
ROT
G0 Z50 M5
M30
Результат обработки на рис. 23
Рис 23.
35
Посмотрим теперь, а что же токарный станок? Здесь то же самое, только
гораздо проще, поскольку обычный токарный станок имеет всего две координаты:
ось Х и ось Z. Но, несмотря на это, на нѐм тоже можно творить удивительные вещи.
Что может быть повторяющимися структурами при токарной обработке?
наверное, только канавки различного профиля. Рассмотрим одну из таких канавок.
Пример 3. На рисунке 24 представлена деталь.
Рис. 24
Три конических канавки расположены относительно друг от друга на разных
расстояниях. Программирование с циклом FOR не проходит. Значит, подпрограмма.
Канавки формируются прорезным резцом, ширина пластины которого составляет 3 мм.
Начало отсчѐта в подпрограмме точка 1. Пусть подпрограмма обработки таких канавок
называется KAN1.SPF . Еѐ текст в относительной системе отсчѐта имеет вид:
; подпрограмма KAN1.SPF
G1
G91 Z-5
; сдвиг на 2 мм + ширина пластины
G90 G1 X20
; проход до диаметра 20 мм
G0
X31
; возврат
G91 Z-1
; сдвиг на 1 мм
G90 G1 X20
; 2 проход, основание канавки сформировано
G0
X31
G91 Z-2
; выход на левый скос
G90 G1 X30
; касание
G91 Z2 X-10
; левый скос
G0 G90 X31
36
G91 Z3
G1 G90 X30
G91 X-10 Z-2
Z-1
G0 G90 X31
M17
; выход на правый скос с учетом ширины пластины
; касание
; правый скос, прорез правым углом пластины
; подчистка дна
Главная программа:
; заготовка W58, D30
T1 D1
; прорезной резец CERATIZIT E-20252
M4 S1000 F0.05
G0 X31
Z-2
MCALL KAN1
Z-2 X31
; выход в точку
Z-18
; выход в точку
Z-40
; выход в точку
MCALL
G0 X40
Z100 M5
M30
Результат на рисунке 25.
Рис. 25
37
2.3. Подпрограммы, составленные в абсолютной системе отсчѐта
Такие подпрограммы пишутся относительно выбранного нуля в абсолютной
системе отсчѐта. При вызове таких подпрограмм в главной программе необходимо
сдвигать начало координат при помощи фрейма TRANS/ATRANS. Иначе подпрограмма будет выполнять всегда около текущего нуля.
Рассмотрим пример, изображѐнный на рис. 22. Пусть подпрограмма называется
OKNO.SPF, начальная точка та же. Также предполагаем, что в центрах окон просверлены
технологические отверстия.
Ниже представлен текст подпрограммы.
; подрограмма OKNO.SPF
; аБс система отсчета
G1 G90
FOR R1=1 TO 3
G91 Z-5.4
G90
G42 Y7.5
X15
Y-7.5
X-15
Y7.5
X0
G40 Y0
ENDFOR
Z1
M17
Главная УП:
T1 D1 M6
M3 S1000 F100
G54 G0 X35 Y30
Z1
MCALL OKNO
TRANS X35 Y30
X0 Y0
TRANS
TRANS X90 Y40
X0 Y0
TRANS
TRANS X150 Y25
X0 Y0
TRANS
MCALL
TRANS X145 Y115
X0 Y0
AROT RPL=90
; фреза 10 мм
; многократный вызов подпрограммы
; сдвиг нуля
; 1 окно
; сброс
; 2 окно
; 3 окно
; отмена многократного вызова
; 4 окно с поворотом на 90 град
38
OKNO
TRANS X50 Y108
X0 Y0
AROT RPL=45
OKNO
TRANS
G0 Z50 M5
M30
; 5 окно с поворотом на 45 град
Результат на рисунке 23. Можете мне поверить.
Для токарного станка рассмотрим эскиз детали, представленной на рис. 24.
Условия те же, но подпрограмма будет составлена в абсолютной системе отсчѐта.
Пусть она называется KAN2.SPF. Текст еѐ приведен ниже
; подпрограмма KAN2.SPF
; заготовка W60, D30
G1 G90
Z-7
X20
G0 X31
Z-8
G1 X20
G0 X31
Z-10
G1 X30
X20 Z-8
G0 X31
Z-5
G1 X30
X20 Z-7
Z-8
G0 X31
M17
Главная программа:
T1 D1
; прорезной резец CERATIZIT E-20252
M4 S1000 F0.05
G0 X31
Z-2
MCALL KAN2
; многократный вызов подпрограммы
TRANS Z-2
; смещение нуля
Z0
TRANS Z-18
Z0
TRANS Z-40
Z0
MCALL
39
G0 X40
Z100 M5
M30
Результат на рис. 25.
Программист сам выбирает в какой системе отсчѐта разрабатывать свою
подпрограмму. Они всѐ равно разовые, конкретно под определенные размеры
заготовки или детали.
40
2.4. Подпрограммы с параметрами R.
Подпрограммы можно сделать более универсальными, если при их разработке
использовать предопределѐнные параметры R. Далее, когда рассмотрим математические
действия с параметрами, остановимся на этом подробнее.
Рассмотрим снова пример, изображѐнный на рисунке 22. Если в главной
программе указать габаритные размеры окон в параметрах, а в подпрограмме при
перемещениях их указывать, то с помощью такой подпрограммы можно вырезать
окна различных размеров.
Главная программа:
; заготовка 0-X-200, 0-Y160, Z1=15, Z2=10
G54 G0 X35 Y30
R2=50
; ширина прямоугольника
R1=40
; высота
Z1
MCALL FEN1
; вызов подпрограммы FEN1
G0 X35 Y30
; 1 окно
G0 X90 Y40
; 2 окно
G0 X150 Y25
; 3 окно
MCALL
R1=30
R2=40
G0 X145 Y115
ROT RPL=90
FEN1
ROT
; новые размеры
R1=20
R2=60
G0 X50 Y108
ROT RPL=45
FEN1
ROT
G0 Z50 M5
; новые размеры
; 4 окно с поворотом на 90 град
; 5 окно с поворотом на 45 град
M30
Подпрограмма написана в относительной системе отсчѐта. Здесь используется
неизвестный нам пока символ < / >. Это деление.
; подпрограмма FEN1.SPF
G1 G91
;
FOR R0=1 TO 3
; 3 прохода
Z-5.5
41
G42 Y=R1/2
X=R2/2
Y=-R1
X=-R2
Y=R1
X=R2/2
G40 Y=-R1/2
ENDFOR
G90 Z1
M17
; половина высоты
; половина ширины
; возврат в абсолютную систему отсчёта
Результат на рисунке 26.
Рис. 26
Подпрограмму можно сделать ещѐ более универсальной, добавив два параметра:
R3 – величина съѐма материала за один проход и,
R4 – количество проходов.
42
2.5. Подпрограммы с передачей параметров.
Определение подпрограммы с передачей параметров осуществляется кодовым
cловом PROC и полным списком ожидаемых параметров. Завершается такая
подпрограмма кодом RET.
Синтаксис:
PROC <Имя ПП> <список параметров>
…
…
RET
Обозначения: < Имя ПП>
– имя подпрограммы
<список параметров> - полный список принимаемых параметров (max 127)
с типом данных и значением
RET
- возврат из подпрограммы.
Например: PROC MUMU (REAL VVV, INT WWW, и т.д.)
Здесь VVV - переменная вещественного типа,
WWW – переменная целого типа.
Вид главной программы следующий:
…
…
MUMU (5.43,10, …)
…
В подпрограмме переменной VVV присваивается значение 5.43, а WWW=10.
Эти данные обрабатываются подпрограммой и после обработки управление
передаѐтся в главную программу.
Рассмотрим небольшой пример. На рисунке 27
Рис. 27
43
представлены четыре глухих отверстия различной глубины- Ø20 мм глубина 10 мм,
Ø30 мм – 8.5 мм, Ø22 мм - -5 мм, Ø35 мм - -2 мм. Требуется разработать одну
подпрограмму для растачивания всех этих отверстий. Пусть подпрограмма называется
KREIS.SPF. Ниже еѐ текст.
; подпрограмма KREIS.SPF
; растачивание отверстий различного диаметра и глубины
PROC KREIS (REAL RR, REAL ZZ)
; переменные RR и ZZ вещественного типа, радиус и глубина соответственно
; из главной программы считываются их значения
G1 Z=ZZ
; врезание
G42 Y=RR
; обработка окружности с коррекцией на радиус инструмента
G2 J=-RR
G1 G40 Y0
Z=1
RET
Текст главной УП
; заготовка 0-X-100, 0-Y-100, Z1=30, Z2=20
T1 D1 M6
M3 S1000 F100
G54 X0 Y0 Z1
; фреза 10 мм
TRANS X20 Y20
X0 Y0
KREIS (10,-10)
; сдвиг координат
; вызов подпрограммы, 1 параметр-радиус 10 мм
;
2 параметр-глубина -10 мм
TRANS X70 Y30
X0 Y0
KREIS (15,-8.5)
ATRANS X-5 Y35
X0 Y0
KREIS (11,-5)
; относительный сдвиг к отв. D22 мм
ATRANS X-35 Y10
X0 Y0
KREIS (17,-2)
G0 Z50 M5
M30
Результат на рисунке 28.
44
Рис. 28
Пусть Вас не смущают недорезы. Это просто пример. Далее уберѐм эти
недостатки и составим более универсальную программу, введя переменные
радиуса фрезы, количества проходов, т.е. постараемся, чтобы дно отверстий было
чистое.
45
3. ГИБКОЕ ПРОГРАММИРОВАНИЕ (немного теории)
3.1. Переменные
Переменные используются вместо фиксированных значений для повышения
гибкости программы. Используя переменные, можно создавать универсальные
программы, создав библиотеку которых, значительно сократить затраты времени
на программирование.
Переменные
• Предопределенные переменные (арифметические параметры R0-R99)
• Переменные, определяемые пользователем
• Системные переменные
Тип переменных
- целые со знаком, диапазон значений: ±(2³¹-1)
- вещественные со знаком, диапазон значений: ±(10ˉ³ºº÷10³ºº)
- Булевы значения: TRUE (1) и FALSE (0), диапазон значений: 1, 0
- один ASCII символ, определяемый кодом, диапазон значений: 0÷255
- строка символов, количество символов в квадратных скобках,
длина строки до 200 символов
AXIS
- идентификатор оси/шпинделя
FRAME - геометрические данные для статической трансформации координат.
INT
REAL
BOOL
CHAR
STRING
Далее будем использовать переменные типа INT, REAL и R-параметры.
Определение переменных пользователя
Производится командой
DEF < Тип переменной><Имя>=<Значение>
Тип переменной – INT, REAL (для нашего случая)
Имя
– наименование переменной (может содержать до 32 буквенноцифровых символов, включая символ нижнего подчѐркивания.
Первые два символа должны быть буквами или нижним
подчѐркиванием.
Равно «=»
– знак присваивания
Значение
– число, соответствующее типу переменной.
Если переменная определяется без начального значения, системой ей присваивается
значение нуля.
Примеры.
DEF INT _M1=3
; определяется целочисленная переменная _M1 с начальным
; значением 3
DEF REAL NM1=2.3 NM2
; определяются вещественные переменные NM1 и NM2
; с начальными значениями 2.3 и 0 соответственно.
46
3.2. Функции вычисления
Функции вычисления в основном используются для R- параметров и переменных
(или постоянных) типа REAL. Типы переменных INT и CHAR также допускаются.
Оператор/функция
вычисления
+
–
*
/
DIV
SIN( )
COS( )
TAN( )
ASIN( )
ACOS( )
SQRT( )
ABS( )
POT( )
TRUNC( )
ROUND( )
LN( )
EXP( )
MINVAL( )
MAXVAL( )
Значение
сложение
вычитание
умножение
деление, при делении тип INT/ тип INT= тип REAL
например: 4/5=0.8
деление для типа переменных INT и REAL
тип INT/тип INT=тип INT ; 4/5=0
синус угла
косинус
тангенс
арксинус
арккосинус
корень квадратный
абсолютное значение
квадрат числа
выделение целой части дробного числа
округление до целого
натуральный логарифм
показательная функция
меньшее значение из двух переменных
большее значение из двух переменных
Для функций вычисления действуют обычные математические правила.
Приоритет операций можно изменить посредством круглых скобок, глубина вложения
до шести. При вычислении тригонометрических функций угол должен быть представлен
в виде десятичной дроби. Например угол 30º30΄ должен быть задан как 30.5º.
Примеры.
R1=R1+2
; значение R1 увеличивается на 2 и результат
; заносится в R1
R1=R2*R1
; результат умножения заносится в R1
R3=(LIN–R4)*2
; результат вычитания удваивается и заносится в R3
R4=SQRT(POT(_X)+POT(_Y))
; текущие значения переменных _X и _Y возводятся
; в квадрат, суммируются, из суммы извлекается
; квадратный корень и заносится в R4
R0=R1–R2+R3/R4
; вычисление по правилам математики
G2 J=–R1
; прорисовать окружность, значение радиуса которой
; находится в R1
47
3.3. Безусловные программируемые переходы
Переходы осуществляются на определенные метки, которые назначаются
программистом. Метка – буквенно-цифровая последовательность, оканчивающаяся
символом двоеточие «:». Всегда стоит в начале строки или после номера кадра.
Например:
BEGIN:
; метка в отдельной строке
BEG: G0 X100 Y100
…
…
; метка, совмещѐнная с кадром УП
Переходы на метки осуществляются с помощью команд GOTOB, GOTOF, GOTO,
GOTOC. Существует ещѐ один безметочный переход GOTOS – это переход на
начало программы.
Синтаксис:
GOTOB METKA
; переход в направлении к началу программы
GOTOF METKA
; переход в направлении к концу программы
GOTO
; оператор перехода с поиском цели. Сначала поиск
; осуществляется в направлении к концу программы,
; потом в направлении начала программы.
METKA
GOTOC METKA
Пример.
; аналогично с GOTO с той разницей, что ошибка 14080
; «Цель перехода не найдена» подавляется и выполнение
; программы продолжается со следующей за GOTOC
; строки программы.
…
B1:
; бесконечная программа
G1 X0 Y0
X100
Y100
X0
Y0
GOTOB B1
M30
48
3.4. Операторы сравнения и логические операторы
Операции сравнения могут использоваться для формулировки условий перехода.
Возможно сравнение и сложных выражений. В основном используется с оператором
IF (если).
Операции сравнения могут использоваться для переменных типа INT, REAL,
BOOL, CHAR. Для типа CHAR сравнивается кодовое значение.
Логические операторы служат для связи значений истинности. Применяются
Только для переменных типа BOOL. Через внутреннее преобразование типов они
могут использоваться и для типов данных CHAR, INT, REAL.
Для логических (булевых) операций для типов данных BOOL, INT, REAL, CHAR
действует:
• ноль соответствует FALSE
• отличное от нуля – TRUE.
Оператор сравнения
Значение
равно
не равно
больше, чем
меньше, чем
больше или равно
меньше или равно
==
<>
>
<
>=
<=
Логический оператор
Значение
ИЛИ
И
Отрицание
Исключающее ИЛИ
AND
OR
NOT
XOR
Между логическими операторами и операндами необходимо вставлять пробелы.
Пример 1.
Пример 2.
…
BEGIN:
R2=R2+1
…
IF (R2<=10) GOTOB BEGIN
…
; пока R2 меньше или равно 10,
; переходить метку BEGIN
…
IF (R1==0) AND (R3> 15) GOTOF END ; если одновременно R1=0 и
; R3>15, перейти на метку END
…
; если нет – продолжить выполнение
…
; программы
END:
…
49
3.5. Приоритет операций
Каждому оператору соответствует приоритет. При обработке выражения сначала
всегда используются операторы с более высоким приоритетом. В случае равнозначных
операторов обработка выполняется слева направо.
В арифметических выражениях посредством круглых скобок можно изменять
порядок вычисления, отличный от обычных правил.
Приоритетность операторов (от высших к низшим)
1
2
3
4
5
6
7
NOT
*, /, DIV
+, –
AND
XOR
OR
==, < >, >, <, >=, <=
Отрицание
Умножение, деление
Сложение, вычитание
Логическое И
Исключающее ИЛИ
Или
Операторы сравнения
50
3.6. Ветвление программы. Оператор CASE…OF…DEFAULT
Функция CASE предлагает возможность проверки актуального значения (тип: INT)
переменной или функции вычисления и в зависимости от результата перейти на
различные места в программе.
Синтаксис:
CASE(<выражение>) OF <Постоянная_1> GOTOF <Цель перехода_1>
<Постоянная_2> GOTOF <Цель перехода_2> … DEFAULT GOTOF
<Цель перехода_n>
Значение:
CASE
Оператор перехода.
<выражение>
Переменная или функция вычисления.
OF
Кодовое слово для формулировки условных ветвлений.
<Постоянная_1>
Первое указанное постоянное значение для переменной
или функции вычисления. Тип: INT.
<Постоянная_2>
Второе указанное постоянное значение для переменной
Или функции вычисления. Тип: INT.
DEFAULT
Если переменная или функция вычисления не
принимает ни одного из указанных постоянных
значений, с помощью этого оператора можно
определить цель перехода.
Если оператор DEFAULT не запрограммирован,
то в этом случае выполняется следующий за
оператором CASE кадр.
GOTOF
Оператор перехода с целью перехода в направлении
конца программы.
Вместо GOTOF могут быть запрограммированы
и все другие команды GOTO.
<Цель перехода_1> Выполняется ветвление на эту цель перехода, если
значение переменной или функции вычисления
равно первой указанной постоянной.
Цель перехода может быть указана или меткой,
определѐнной программистом, или номером кадра,
например, N100.
<Цель перехода_2> Выполняется переход на эту цель, если значение
переменной или функции вычисления равно второй
указанной постоянной.
<Цель перехода_n> Выполняется переход на эту цель, если переменная
не принимает ни одного из указанных постоянных
значений.
51
Пример.
DEF INT MM1 MM2 MM3
…
…
CASE(MM1+MM3-MM2) OF 6 GOTOF L1 8 GOTOF L2 DEFAULT GOTOF END
L1:
…
L2:
…
END: MSG (“ ПРОЦЕСС ПРОШЕЛ”)
…
Комментарии.
Переменные ММ1, ММ2, ММ3 определяются как целые.
Оператор CASE определяет следующие возможности ветвления программы:
1.
Если вычисленное выражение в скобках равно 6, то переход на метку L1.
2.
Если вычисленное выражение равно 8, то переход наметку L2.
3.
Если значение функции вычисления ни 6, ни 8, то перейти на метку END.
Под меткой END стоит конструкция MSG. Это оператор выдачи текстового
сообщения на дисплей станка во время отработки программы. Формат его следующий:
MSG (“ текст сообщения “).
52
3.7. Управляющие структуры
Система ЧПУ обрабатывает кадры УП в запрограммированной последовательности.
Эта последовательность может изменяться через программирование программных
циклов и программных циклов. Программирование управляющих структур осуществляется с помощью элементов управляющих структур (кодовых слов):
IF…ELSE, LOOP, FOR, WHILE и REPEAT.
3.7.1. Программный цикл с альтернативой (IF, ELSE, ENDIF)
Конструкция с IF и ELSE используется, если программный цикл должен
содержать альтернативный программный блок: если условие IF выполнено, выполняется
следующий за IF программный блок. Если условие не выполнено, выполняется
следующий за ELSE альтернативный программный блок. После отработки программного
блока управление передаѐтся на кадр, следующий за оператором ENDIF.
Если альтернативы не требуется, то цикл IF может быть запрограммирован
и без оператора ELSE и следующего за ним альтернативного программного блока.
Синтаксис.
IF (<условие>)
…
ELSE
…
ENDIF
Значение.
IF
Запускает цикл IF
ELSE
Запускает альтернативный блок
ENDIF
Конец цикла IF
<условие>
Условие, определяющее какой программный блок будет пройден.
Пример.
IF (R1==0)
…
ELSE
…
ENDIF
…
Если R1=0, выполняется программный блок, следующий за оператором IF.
Если R1≠0, выполняется программный блок, следующий за оператором ELSE.
3.7.2. Счѐтный цикл ( FOR … TO …, ENDFOR)
Рассмотрен в главе 1.2.
53
3.7.3. Бесконечный программный цикл (LOOP, ENDLOOP)
Бесконечный цикл используется в бесконечных программах. Концом цикла
всегда является возврат на начало цикла.
Синтаксис.
LOOP
…
ENDLOOP
Значение.
LOOP
Запускает бесконечный цикл
ENDLOOP
Конец цикла и возврат на начало
3.7.4. Программный цикл с условием в начале цикла ( WHILE, ENDWHILE)
В цикле WHILE условие стоит в начале цикла. Цикл выполняется до тех пор,
пока выполняется условие.
Синтаксис.
WHILE <условие>
…
ENDWHILE
Значение.
WHILE
Запускает цикл
ENDWHILE
Конец цикла, возврат на начало
<условие>
Условие, которое должно выполняться, чтобы
выполнялся цикл WHILE
Пример.
R1=0
WHILE R1<=10
…
…
R1=R1+1
ENDWHILE
…
54
3.7.5. Программный цикл с условием в конце цикла (REPEAT, UNTIL)
В цикле REPEAT условие стоит в конце цикла. Цикл выполняется один раз
и затем повторяется до тех пор, пока выполняется условие.
Синтаксис.
REPEAT
…
…
UNTIL <условие>
Значение.
REPEAT
Запускает цикл.
UNTIL
Конец цикла и возврат на начало.
<условие>
Проверка условия и, если выполняется,
возврат на начало цикла.
Пример.
R2=0
REPEAT
R2=R2+1
…
…
UNTIL R2<=10
…
55
3.8. Подавление отображения текущего кадра (DISPLOF, DISPLON)
При использовании функции DISPLOF подавляется отображение текущего
кадра подпрограммы на дисплее станка. Вместо мелькания текущих кадров
на дисплее отображается вызов цикла или подпрограммы.
Синтаксис.
PROC … DISPLOF
Значение.
PROC
подпрограмма
DISPLOF
отмена отображения текущего кадра
Для включения отображения текущего кадра используется функция DISPLON.
PROC … DISPLON
56
4. ГИБКОЕ ПРОГРАММИРОВАНИЕ (ПРИМЕРЫ)
4.1. Программирование нелинейных фигур на плоскости XOY (G17)
Если траекторию, вдоль которой движется инструмент, можно представить
в математическом виде, и получившаяся функция будет непрерывной, то, изменяя
аргумент и вычисляя соответствующие значения функции, можно передвигать
инструмент по полученным координатам параллельно вычислительному процессу,
получая тем самым в наглядном виде график этой функции. Рассмотрим в этой главе
три примера: функции y=sin x, y=(sin x)/x и эллипс.
4.1.1. Тригонометрическая функция Y=SIN (X)
Применяя полученные знания, попытаемся двинуть фрезу по синусоидальному
закону. Возьмѐм функцию y=20sin(x) и прочертим фрезой еѐ график на отрезке
[–360º, 360º]. Коэффициент 20 взят для повышения наглядности. Текст такой УП
имеет вид:
MSG ("SINUS")
; функция Y=20*SIN(X)
; фреза шаровая 2 мм
; заготовка 105-X-105, 25-Y-25, Z1=10, Z2=5
R1=-360
R2=-100
R3=0
R4=ABS(R2/R1)
; начальный угол
; начало по оси Х
; значение функции
; приращение по Х, соответствующее одному градусу
T6 D1 M6
M3 S1000
G0 G54 X-105 Y0
; прорисовка осей
G1 Z1 F500
Z-0.2 F100
X105
Z1
X0 Y40
Z-0.2
Y-40
Z1
X0 Y0
G0 X=-100 Y=20*SIN(R1)
; выход в начальную точку
G1 Z-0.4
BEG: R3=20*SIN(R1)
G1 X=R2 Y=R3
; движение фрезы
R1=R1+1
; изменение угла на 1 градус
R2=R2+R4
; вычисление координат по оси Х
IF R1<=360 GOTOB BEG ; переход на метку BEG, пока выполняется условие
G0 Z50 M5
57
M30
Результат на рисунке 29.
Рис.29
Если поменять SIN на COS, получим график функции y=20cos(x).
Результат такой замены представлен на рис. 30.
Рис. 30
58
4.1.2. График функции Y=SIN(X)/X
При построении графика такой функции может возникнуть неопределенность.
При значении аргумента Х=0 получается, что Y=0/0. Раскрывая неопределенность,
получаем, что при Х=0 Y=1. Да ещѐ видим, что функция чѐтная, т.е. f(x)=f(-x), значит
можно начать от Х=0 до 6π, а после сделать зеркальное отображение относительно
оси Y в отрицательную область.
Для повышения наглядности введем коэффициент 50, и функция примет вид:
y=50(sin x/x). Ход мыслей программиста будет виден из комментариев в программе.
УП имеет вид:
; функция Y=50*SIN(X)/X
; фреза шаровая 2 MM
; заготовка 105-X-105, 20-Y-60, Z1=10, Z2=15
;
R1=0
; начальный угол
R2=0
; начало по оси Х
R3=0
; значение функции
R4=0.0175
; приращение по Х, соответствующее одному градусу
; 3.14/180=0.0175
T6 D1 M6
M3 S1000
G0 G54 X-105 Y0
; прорисовка осей
G1 Z1 F500
Z-0.1 F100
X105
Z1
X0 Y105
Z-0.1
Y-20
Z1
G0 X0 Y50
; выход в начальную точку
;
FOR R0=1 TO 2
G1 Z-0.3
BEG: R1=R1+1
; изменение на 1 градус
R2=R2+R4
R3=50*(SIN(R1)/R2)
G1 X=5*R2 Y=R3
; 5-масштабный коэффициент для оси Х
IF R1<=1080 GOTOB BEG
; переход на метку BEG, пока выполняется условие
R1=0
; сброс параметров в исходное состояние
R2=0
Z1
G0 X0 Y50
AMIRROR X0
; зеркальность относительно оси Y
ENDFOR
G0 Z50 M5
M30
59
Результат выполнения программы представлен на рис. 31.
Рис. 31
60
4.1.3. Эллипс
Каноническое уравнение эллипса имеет вид:
+
=1
, где
а - большая полуось эллипса (ось, параллельная оси абсцисс)
b - малая полуось эллипса (параллельная оси ординат)
Представим уравнение эллипса в виде y(x). После несложных преобразований имеем
y=b
Если в параметр R1 ввести значение полуоси а, в R2 значение полуоси b,
а в R3 – значение аргумента, то в машинном виде уравнение эллипса примет вид:
Y=R2*SQRT(1-POT(R3)/POT(R1)).
Ниже представлен текст УП для фрезерования эллипса. Занося в R1и R2
различные данные, можно получить желаемый эллипс.
;
; Пример параметрического программирования эллипса
;
MSG ("ELLIPS")
;
; фреза шаровая 2 мм
; заготовка 50-X-50, 50-Y-50, Z1=10, Z2=15
; R1,R2-полуоси эллипса
R1=50
; полуось эллипса А
R2=25
; полуось эллипса В
R3=0
; аргумент
R4=0
; функция
;
;
;
Y=B*SQRT(1-POT(X)/POT(A))
T6 D1 M6
M3 S1000 F100
G0 G54 X=-R1 Y0 Z1
; выход на левый край оси А
G1 Z-0.2 F100
R3=-R1
BEG:
; верхняя часть
R4=R2*SQRT(1-POT(R3)/POT(R1))
61
G1 X=R3 Y=R4
R3=R3+1
IF (R3<=R1) GOTOB BEG
R3=R1
R1=-R1
BEG1:
R4=R2*SQRT(1-POT(R3)/POT(R1))
G1 X=R3 Y=-R4
R3=R3-1
IF (R3>=R1) GOTOB BEG1
;
G1 Z50 F1000
M5
M30
; изменение аргумента на 1 мм
; переустановка параметров
; нижняя часть
Из формулы эллипса видим, что окружность – частный случай эллипса.
В этом легко убедиться, если в УП значения полуосей задать одинаковыми.
Результат выполнения этой УП на рис. 32
Рис. 32
62
Если вместо шаровой фрезы поставить концевую, в программу добавить
пару отверстий под шурупы и отфрезеровать пару цифр, то можно открыть артель
по производству квартирных или офисных номерков. Угадайте номер моей квартиры.
Рис. 33
63
4.2. Параболоид
С помощью параметров довольно легко программировать различные тела
вращения. Рассмотрим это на примере параболоида, представленного на рис. 34.
Рис. 34
Текст УП
; парабола Z=-0.2*POT(X)
; заготовка W=40, D=20 мм
;
T12 D1
; резец SDJC L1212
M4 S1000 F0.1
G0 X10 Z1
; подготовительный проход
G1 Z0
Z-5 X20
G0 Z1
X-0.8
; выход за ось Х на радиус пластины
G1 Z0
R2=0
;X
R3=0
;Z
;
BEG:
R2=R2+0.1
R3=-0.2*POT(R2)
G1 G42 X=2*R2 Z=R3
; движение с коррекцией на радиус пластины
IF R2<=10 GOTOF BEG
;
G0 G40 X40
Z100 M5
M30
Результат работы программы на рисунке 35.
64
Рис. 35
Изменяя коэффициент в формуле параболы, можно выточить любой параболоид.
65
4.3. Программирование цилиндрической резьбы, профиль которой
изменяется по косинусоидальному закону.
Нигде не видел такого профиля, это просто пример, показывающий
возможности параметрического программирования. Рассмотрим пример на рис. 36.
Рис. 36
Шаг такой резьбы 10 мм. Коэффициент при косинусе единица, значит
величина профиля 2 мм.
Текст УП:
MSG ("COSINUSGEWINDE")
;
R1=26
;диаметр заготовки
R2=20
;количество циклов
R3=0
;текущий диаметр
R4=0
;приращение по оси Z
R5=10
;шаг резьбы
R6=1
;коэффициент при COS(X)
R7=0
;текущее значение угла
R8=0
;средний диаметр
R9=0
;приращение угла
R10=80
;длина резьбы
; резец SDNC N1212
; заготовка W=100, D=26 мм
T9 D1
M3 S200 F0.05
G0 Z=R5 X=R1
; выход на диаметр и на шаг резьбы за заготовку
;
R8=R1-2*R6
R9=360/R2
; приращение угла на один проход
66
R4=R5/R2
BEGIN:
R3=R8+2*R6*COS(R7)
G1 X=R3
G91 G33 Z=-R10 K=R5
G90 G0 X=R1+2
G91 G0 Z=R10-R4
G90 X=R3
R7=R7-R9
IF (R7>=-360) GOTOB BEGIN
G0 X50
Z100
M5
M30
Результат на рисунке 37.
Рис. 37
Резьба на этом виде сбоку показана условно. На реальной детали всѐ как надо.
Как говорят мои коллеги, такую штуку легко выточить на универсальном станке,
в чем я сильно сомневаюсь. Но следующую вещь, они сказали, вручную сделать нельзя.
67
4.4. Программирование конической резьбы, профиль которой изменяется
по косинусоидальному закону.
Рассмотрим рисунок 38.
Рис. 38
То же, что и в предыдущем случае, только резец движется по образующей
конуса. Ниже представлен текст УП. Программирование резьбы оформлено
через переменные.
T12 D1
M4 S1000 F0.1
G0 Z0
X30
G1 X-1
X25
Z-70
X26
;
G0 Z1
X20
G1 X25 Z-20
;
G0 Z1
X15
G1 X25 Z-40
;
G0 Z1
X10
G1 Z0
X25 Z-60
G0 X50
Z100
M5
; резец SDJC L1212
; подготовка конической поверхности
68
T9 D1
; резец SDJC N1212
M3 S200 F0.05
;
DEF REAL DD=5.5
; начальный радиус средней линии
DEF REAL UGOL=0
; угол в косинусоидальной функции
DEF REAL DZ=50
; длина резьбы минус шаг
DEF REAL DDX=0
; приращение по Х к средней линии в зависимости от угла
;
G0 Z10 X7.5
; выход в начальную точку с учетом конусности
;
BEGIN:
DDX=DD+2*COS(UGOL)
G0 X=DDX
G90 G33 X=15+DDX Z= -DZ K=10
G0 G90 X30
G91 G0 Z59.75
; за счет функции G91 обеспечивается постоянный сдвиг
; начальной точки по оси Z
DD=DD+0.0625
; увеличивающийся радиус средней линии
DZ=DZ+0.25
G90
UGOL=UGOL-9
IF (UGOL>=-360) GOTOB BEGIN
;
G0 G90 X50
Z100
M5
M30
Результат на рисунке 39.
Рис. 39
69
4.5. Программирование цилиндрической «веревочной» резьбы.
Рассмотрим рисунок 40.
Рис. 40
Профиль резьбы – часть окружности диаметром 12 мм. Резьба оформлена
через цикл FOR. Уравнение окружности имеет вид:
(z+4.5)² + (x-16.5)² = 36 , отсюда
X1,2=16.5±
Выбираем
.
x=16.5–
.
Подставляя вместо (x) R2, a вместо (z) R1, запишем формулу в машинном виде:
R2=16.5–SQRT(36–POT(R1+4.5))
УП имеет вид:
; заготовка W=80, D=25
;
T9 D1
; резец SDJC N1212
M4 S200 F0.1
;
G0 Z0 X25
R1=0
;Z
R2=0
;X
;
FOR R3=1 TO 18
; резьба нарезается за 18 проходов
R1=R1-0.5
R2=16.5-SQRT(36-POT(R1+4.5)) ; вычисление Х на дуге окружности
70
G1 Z=R1 X=2*R2
G33 G91 Z-60 K=12
G0 G90 X26
Z=R1
ENDFOR
G0 X26
Z10 M5
M30
; резьБа
Результат на рисунке 41.
Рис. 41
Как видим, владея техникой параметрического программирования, можно
нарезать резьбу с любым нестандартным профилем, естественно, если есть резец
с пластиной с соответствующими углами.
71
4.6. Программирование скосов.
Обычно обработка на 3-х координатном фрезерном станке с ЧПУ ведется в
формате 2.5D, т.е., движение инструмента в плоскости G17 на разных глубинах или
высотах в зависимости от того, где выбран ноль по оси Z. И вдруг, наклонная плоская
поверхность или сферическая. Как быть? Не надо отчаиваться. Программирование
с параметрами поможет и здесь. Посмотрим на рисунок 42.
Рис. 42
Скосы можно программировать или от основания, или от вершины.
Желательно от основания, поскольку при программировании от вершины
происходит зарез фрезы в тело заготовки. Просто нужно руководствоваться
целесообразностью. В данном случае в плоскости G17 за ноль выберем центр
детали, а по оси Z верхнюю плоскость. Скос можно программировать с помощью
цикла FOR или переходом по условию. Остановимся на последнем. Техника
программирования проста: в зависимости от чистоты обработки выбирается
шаг по оси Х или по оси Z, неизвестный шаг (или Х, или Z) вычисляется через
тангенс угла α. Текст УП представлен ниже.
72
;
; Заготовка
Пример программирования скосов
0-X-20,20-Y-20,Z1=27, Z2=30
R1=0
;Х
R2=0.5
; приращение по Z
R3=R2*15/25
; приращение по X (ΔХ=ΔZ*tgα)
;
T1 D1 M6
; фреза 10 мм
M3 S1000 F100
G0 G54 X-5 Y26 Z1 ; выход в исходную точку с учетом радиуса фрезы
G1 Z0
R2=0
BEG:
;
R1=R1+R3
R2=R2+0.5
IF (R2>25) GOTOF END
G1 X=-(R1+5) Z=-R2
Y-26
R2=R2+0.5
IF (R2>25) GOTOF END
R1=R1+R3
G1 X=-(R1+5) Z=-R2
Y26
;
GOTOB BEG
END:
G0 Z50 M5
M30
Результат на рисунке 43.
Рис.43
73
Если повернуть скос на 180º, получится два скоса, если на 120º – трѐхгранная
пирамида, на 90º – четырѐхгранная и т.д. Добавим в программу пару кадров и получим
пятигранную пирамиду. Текст УП приведен ниже.
;
; Заготовка
0-X-20,20-Y-20,Z1=27, Z2=30
;
R1=0
;Х
R2=0.5
; приращение по Z
R3=R2*15/25
; приращение по Х
;
T1 D1 M6
; фреза 10 мм
M3 S1000 F100
G0 G54 X0 Y0 Z1 ; выход в ноль
G1 Z0
FOR R0=1 TO 5
; количество циклов=количеству граней
R2=0
X-5 Y26
BEG:
R1=R1+R3
R2=R2+0.5
IF (R2>25) GOTOF END
G1 X=-(R1+5) Z=-R2
Y-26
R2=R2+0.5
IF (R2>25) GOTOF END
R1=R1+R3
G1 X=-(R1+5) Z=-R2
Y26
GOTOB BEG
END:
R1=0
G0 Z0
AROT RPL=72
; 360°/5=72°
ENDFOR
G0 Z50 M5
M30
Эта программа под конкретную пирамиду. Позже составим универсальную
подпрограмму для вытачивания правильных пирамид.
74
4.7. Конические поверхности
Если перемещать инструмент вдоль наклонной прямой, лежащей в плоскости
XOZ или YOZ, и через равные отрезки описывать окружности в плоскости XOY,
то получим коническую поверхность. Чем меньше эти отрезки, тем точнее будет
получаться конус. Соответственно конус может быть полным, если начинать от вершины,
или усечѐнным. Рассмотрим программирование полного конуса, приведенного
на рис. 44.
Рис. 44
Возьмѐм за ноль детали вершину конуса. Фрезу будем вести вдоль образующей
конуса в плоскости YOZ в отрицательной области. Ниже текст УП.
; конус
; заготовка 20-X-20, 20-Y-20, Z1=35, Z2=32
;
T1 D1 M6
; фреза концевая 10 мм
M3 S1000 F100
G0 G54 X-5 Y0 Z1
G1 Z0
R1=0.1
; шаг по оси Z
R2=R1/2
; шаг по оси X, ΔХ=0.1tgα, tgα=15/30=0.5
R3=0
; текущий X
R1=0
ANF:
R1=R1-0.1
R3=R3+R2
75
G1 X=-R3-5
Z=R1
G2 I=R3+5
IF (R1>-30) GOTOB ANF
G1 X-28
; подчистка углов
G2 I28
G0 Z50 M5
M30
Результат на рисунке 45.
Рис. 45
Программируя не полную окружность, а еѐ часть, например, четверть,
можно красиво скруглять углы на деталях.
76
4.8. Цилиндрические поверхности
Если в плоскости XOZ или YOZ фрезу перемещать по дуге окружности,
скажем, через градус, а в плоскости XOY вести фрезу вдоль осей X или Y, то получим
цилиндрическую поверхность (рис. 46).
Рис. 46
Координаты точек на окружности по оси Х в абсолютном виде будут определяться
как Х=Rcos(α), координаты центра фрезы как X=Rcos(α)+r, где r – радиус фрезы.
По оси Z как Z=Rsin(α).
Перемещая фрезу вдоль оси Y из таких точек, получим цилиндрическую
поверхность. Полуцилиндр можно получить, запрограммировав четверть, а потом
сделать зеркальное отображение, или сразу, изменяя угол от 0 до 180°. В таком случае в
верхней точке фрезу нужно сдвинуть на расстояние диаметра фрезы по оси Х или Y.
Рассмотрим пример, приведѐнный на рис. 47
Рис. 47
77
Ниже текст УП. Вторая половина полуцилиндра реализована фреймами
TRANS и AMIRROR.
;
POLUCILINDR
; заготовка 0-X-100,0-Y-50,Z1=30, Z2=27
;
R1=0
; X
R2=0
; Z
R3=0
; угол
R4=20
; радиус
;
T1 D1 M6
; фреза 10 мм
M3 S1000 F100
G0 G54 X5 Y60
Z-20
FOR R5=1 TO 2
G1 X5 Y60
; предварительные проходы
Z-20
Y-10
X15
Y60
X25
Y-10
R3=0
BEG:
; начало обработки полуцилиндра
R1=R4*COS(R3)
R2=R4*SIN(R3)
G1 Z=-20+R2 X=45-R1
Y60
R3=R3+1
IF (R3>90) GOTOF END
R1=R4*COS(R3)
R2=R4*SIN(R3)
Z=-20+R2 X=45-R1
Y-10
R3=R3+1
IF (R3>90) GOTOF END
;
GOTOB BEG
;
END:
TRANS X100 Y0
; сдвиг нуля
AMIRROR X0
; зеркальность
ENDFOR
;
G0 Z50 M5
M30
78
Результат на рисунке 48.
Рис. 48
Задавая начальный угол больше нуля, можно получать цилиндрические
поверхности, центральный угол которых меньше 180°.
79
4.9. Сферические поверхности
Если в предыдущем случае в плоскости XOY проводить не прямые,
а окружности, получим сферическую поверхность. Алгоритм вычисления координат
опорных точек аналогичный. Рассмотрим пример, приведѐнный на рис. 49.
Рис.49
Текст УП:
MSG ("HALBKUGEL")
;
заготовка 21-X-21 , 21-Y-21, Z1=30, Z2=25
;
R1=20
; радиус шара
R2=5
; радиус фрезы
R3=0
;X
R4=0
;Z
R5=0
; угол
;
T1 D1 M6
M3 S1000
G1 G54 X=R2 Y0 F100
;
полушарие
REPEAT
R5=R5+2
R3=-(R2+R1*SIN(R5))
80
R4=R1-R1*COS(R5)
G1 X=R3
Z=-R4
G3 I=-R3
UNTIL (R5>=90)
G1 Z50 F1000
;
M30
Результат на рис. 50.
Рис. 50
81
4.10. Вогнутые цилиндрические поверхности
Программирование таких поверхностей аналогично программированию
выпуклых с той лишь разницей, что используется шаровая фреза (рис. 51).
Рис. 51
При программировании следует указывать движение центра фрезы (указана
штриховой линией). Координаты i-ой точки вычисляются по формулам:
Xi=(R-r)cos(α), Zi=(R-r)sin(α), где
R – радиус полуцилиндра,
r – радиус шаровой фрезы,
α – текущий угол.
Составим УП для фрезерования полуцилиндра, представленного на рис. 52.
Рис. 52
82
Фрезерование проведем, изменяя угол от 0 до 180°.
Текст УП:
; заготовка 40-X-40, 0-Y-50, Z1=25, Z2=20
;
T4 D1 M6
; фреза шаровая 10 мм
M3 S1000 F100
R1=20
; радиус полуцилиндра
R2=5
; радиус фрезы
R3=0
;X
R4=0
;Z
R5=0
; угол от 0 до 180 градусов
;
G0 G54 Y-6 X=-(R1-R2) Z1
G1 Z=-R2
BEG:
IF (R5>180) GOTOF END
G1 X=-(R1-R2)*COS(R5) Z=-(R1-R2)*SIN(R5)-R2
Y56
R5=R5+1
IF (R5>180) GOTOF END
X=-(R1-R2)*COS(R5) Z=-(R1-R2)*SIN(R5)-R2
Y-6
R5=R5+1
GOTOB BEG
END:
G0 Z5 M5
M30
Результат на рис. 53.
Рис. 53
83
4.11. Вогнутые сферические поверхности
Вычисления, аналогичные показанным в главе 4.10., с той лишь разницей,
что из опорных точек, описываются полные окружности. Составим УП для изготовления
детали, представленной на рисунке 54.
Рис. 54
Программирование обработки будем вести с левого края, изменяя угол
от 0 до 90°. Можно вести и от центра, предварительно просверлив технологическое
отверстие соответствующего диаметра. Координаты опорных точек в таком случае
определять согласно эскизу.
Текст УП:
; вогнутая полусфера
; заготовка 40-X-40, 40-Y-40, Z1=25, Z2=20
;
T4 D1 M6
; фреза шаровая 10 мм
M3 S1000 F100
R1=20
R2=5
R3=0
R4=0
R5=0
; радиус полусферы
; радиус фрезы
;X
;Z
; угол от 0 до 90 градусов
G0 G54 Y0 X=-(R1-R2) Z1
G1 Z=-R2
; выход в исходную точку
; врезание до центра шаровой фрезы
84
BEG:
IF (R5>=90) GOTOF END
;
;
;
R3=-(R1-R2)*COS(R5)
R4=-(R1-R2)*SIN(R5)-R2
G1 X=R3 Z=R4
G2 I=-R3
R5=R5+1
GOTOB BEG
END:
G0 Z5 M5
X30 Y30
M30
; при угле, равном 90°, радиус окружности
становится равным нулю, поэтому этот угол
исключается. При программировании от центра
такой угол присутствует в вычислениях
Результат на рисунке 55.
Рис. 55
85
4.12. Программирование объѐмных фигур с одновременным
движением по трем осям
В качестве примера рассмотрим «объѐмную» спираль Архимеда, которая
условно показана на рисунке 56.
Рис. 56
Текст УП:
MSG ("SERPANTIN")
; спираль Архимеда в объёме
;
Заготовка 20-X-20 , 20-Y-20, Z1=42, Z2=37
; фреза 10 мм
;
определение параметров
R1=0
; угол
R2=0
; приращение по Х
R3=0
; приращение по Y
R4=-32
; высота по Z
R5=25
; начальный радиус с учётом радиуса фрезы
R6=0.01
; уменьшение радиуса на 1 градус
R7=0.018
; приращение по Z на один градус
;
T1 D1 M6
M3 S1500 F200
G0 G54 X25 Y0
G1 Z-32
G41 X20
G2 I-20
G1 G40 X25
86
;
BB: R1=R1-1
R5=R5-R6
R2=R5*COS(R1)
R3=R5*SIN(R1)
G1 X=R2 Y=R3
IF R1>-360 GOTOB BB
R1=0
R5=21.4
BEG: R1=R1-1
R5=R5-R6
R2=R5*COS(R1)
R3=R5*SIN(R1)
R4=R4+R7
G1 X=R2 Y=R3 Z=R4
IF R1>-1800 GOTOB BEG
;
G0 Z40
X100
M5
M30
; проход на глубине 32 мм, исключительно
; для придания детали товарного вида
; сброс угла
; R5=25-0.01*360=21.4
; спираль
; 5 витков
Расчѐт параметров.
R7 = R4/5/360≈0.018, где R4=32 – высота, 5 – количество витков, 360 – полный угол.
R6 = (R5-5)/1800≈0.01, где (R5-5) – начальный радиус без радиуса фрезы, 1800=360*5
полное количество градусов.
Результат на рисунке 57.
Рис. 57
87
5. Примеры разработки универсальных подпрограмм
Универсальные подпрограммы – это подпрограммы, которые принимают
значения переменных из главной программы и соответственно этим значениям
выполняют алгоритм, заложенный программистом. Ниже рассмотрим три примера
по разработке таких программ.
5.1. Подпрограмма растачивания отверстий различного диаметра
и глубины фрезой произвольного диаметра
В главе 2.5. у нас случились недорезы и я обещал показать, как разработать
подпрограмму, которая бы исключала эти недостатки. При разработке подпрограмм
обычно устанавливают какие-либо условия, поскольку предусмотреть все возможные
варианты развития событий практически невозможно.
В нашем случае имеется отверстие определенного диаметра, его глубина
и диаметр используемой фрезы.
Назначим переменные. Пусть
D_OTV – переменная, обозначающая диаметр отверстия. Тип REAL
TIEFE – глубина отверстия. Тип REAL
D_FR – диаметр фрезы. Тип INT.
Значения этих переменных будут передаваться из главной программы.
Условия:
1. Ноль детали по осям X, Y – центр отверстия, по оси Z – верхняя плоскость
2. Фреза находится в нуле детали.
Если глубина отверстия больше диаметра фрезы, то растачивание производится
за несколько проходов. Количество проходов определяется как выделение целого от
(TIEFE/D_FR). Последний проход осуществляется на требуемой глубине.
Теперь, используя эти начальные данные, составляется алгоритм решения поставленной
задачи. Их может быть множество. Сколько программистов – столько и алгоритмов.
Вот один из них.
1. Осуществляется деление TIEFE/D_FR.
2. Далее подпрограмма ветвится. Ветвление осуществляется с помощью
конструкции IF… ELSE …ENDIF. Если частное меньше 1, работа производится
на требуемой глубине, если >= 1, то за несколько проходов (1 проход= диаметру
фрезы) + последний проход на конечной глубине.
3. Аналогично программируется растачивание в плоскости XOY.
Ниже приводится текст подпрограммы. Она называется LOCH.SPF.
Обилие комментариев поможет понять мысли программиста.
88
; подпрограмма LOCH.SPF
; растачивание отверстий различного диаметра и глубины
; фрезой заданного диаметра
;
PROC LOCH (REAL D_OTV, REAL TIEFE, INT D_FR) DISPLOF
;
; D_OTV
диаметр отверстия
; TIEFE
глубина
; D_FR
диаметр фрезы
; определение дополнительных переменных
DEF INT PR_HOR
DEF INT PR_VERT
; количество проходов по горизонтали
; количество проходов по вертикали
PR_HOR=TRUNC(D_OTV/(2*D_FR)) ; целая часть при горизонтальных проходах
PR_VERT=TRUNC(TIEFE/D_FR)
; целая часть глубины
R0=0
; сдвиг по горизонтали
IF (PR_VERT<1)
; если глубина отверстия меньше диаметра фрезы
A1: R0=R0+D_FR-1
G1 Z=-TIEFE
FOR R1=1 TO PR_HOR ; цикл растачивания одного горизонтального прохода
G1 G90 Y=R0
G2 J=-R0
R0=R0+(D_FR-1)
ENDFOR
G1 G42 Y=D_OTV/2
G2 J=-(D_OTV/2)
G1 G40 Y0
G0 Z5
RET
; возврат из ПП
ELSE
; если глубина отверстия больше диаметра фрезы
R0=0
FOR R2=1 TO PR_VERT ; цикл захода в глубину
G91 G1 Z=-D_FR
R0=R0+(D_FR-1)
FOR R1=1 TO PR_HOR ; цикл растачивания одного горизонтального прохода
G1 G90 Y=R0
G2 J=-R0
R0=R0+(D_FR-1)
ENDFOR
R0=0
; доработка до нужного диаметра
G1 G42 Y=D_OTV/2
G2 J=-(D_OTV/2)
G1 G40 Y0
ENDFOR
;
ENDIF
GOTOB A1
; переход на доработку остатка по глубине
RET
89
Используя программу, приведенную в главе 2.5. и подпрограмму LOCH,
посмотрим, что получится.
Главная программа:
; заготовка 0-X-100, 0-Y-100, Z1=30, Z2=20
;
T1 D1 M6
; фреза 10 мм
M3 S1000 F100
G54 X0 Y0 Z1
TRANS X20 Y20
X0 Y0
LOCH (20,10,10)
; сдвиг координат
; вызов ПП: 1 параметр - диаметр отверстия
;
2 - глубина
;
3 - диаметр фрезы
TRANS X70 Y30
X0 Y0
LOCH (30,8,10)
;
ATRANS X-5 Y35
X0 Y0
LOCH (22,5,10)
;
ATRANS X-35 Y10
X0 Y0
LOCH (34,2,10)
G0 Z50 M5
M30
Результат на рисунке 58. Сравним с рис. 28.
Рис. 58
90
5.2. Подпрограмма для фрезерования правильных пирамид
Рассмотрим рисунок 59. Правильная четырѐхугольная пирамида, основание
которой вписано в окружность радиусом R. Высота пирамиды Н (при фрезеровании
следует обратить внимание на инструмент или провести предварительную обработку).
Нас интересует в первую очередь тангенс угла α между осью пирамиды и еѐ гранью.
Путем нехитрых вычислений определяем, что тангенс угла α для пирамиды с количеством граней n определяется по формуле
tgα =
, где
R – радиус описанной окружности вокруг основания,
H – высота пирамиды,
n – количество граней.
Условие: Локальный ноль на вершине пирамиды, фреза должна находиться в
локальном нуле.
Рис. 59
Зная тангенс угла α, по накатанному варианту (см. главу 4.6.) программируем
скосы и поворачиваем их обработку на соответствующий угол.
Наименования принимаемых переменных видны из комментариев.
; подпрограмма PIRAMIDA.SPF
; фрезерование правильных пирамид с количеством граней от 3 и более
;
PROC PIRAMIDA (REAL ROKR, REAL HH, INT GRANI, REAL RFR, REAL DZ) DISPLOF
;
; ROKR - радиус описанной окружности
; HH
- высота пирамиды
; GRANI - количество граней
; RFR - радиус фрезы
91
; DZ
- шаг по оси Z
; определение дополнительных переменных
DEF REAL TAN_UGLA
; тангенс угла между осью пирамиды и гранью
DEF REAL DXX=0
; сумма приращений по оси Х
DEF REAL DZZ=0
; сумма приращений по оси Z
DEF REAL DX
; шаг по оси X
TAN_UGLA=ROKR*COS(180/GRANI)/HH ; вычисление тангенса угла
DX=DZ*TAN_UGLA
; шаг по оси Х
FOR R0=1 TO GRANI
; число повторений по количеству граней
G1 X=RFR
; смещение на радиус фрезы
BEGIN:
; начало обработки грани
G1 Y=-ROKR
; смещение вдоль оси Y на минус радиус окружности
DXX=DXX+DX
; суммирование приращений по оси Х
DZZ=DZZ+DZ
; то же по оси Z
IF DZZ>HH GOTOF END1 ; переход на метку END1, если общий Z>высоты пирамиды
G1 X=RFR+DXX Z=-DZZ ; перемещение в точку суммирования
Y=ROKR
; смещение вдоль оси Y
DXX=DXX+DX
DZZ=DZZ+DZ
IF DZZ>HH GOTOF END1
X=RFR+DXX Z=-DZZ
GOTOB BEGIN
; переход на метку BEGIN
END1:
G0 Z0
X=RFR Y0
; возврат в исходную точку
AROT RPL=360/GRANI
; поворот на угол, согласно количеству граней
DXX=0
; обнуление переменных для нового прохода цикла
DZZ=0
ENDFOR
RET
; возврат из ПП
Пример главной программы с пятью пирамидами с различным количеством
граней (рис. 60).
Рис. 60
92
; заготовка 55-X-55, 55-Y-55, Z1=46, Z2=40
T1 D1 M6
; фреза 10 мм
M3 S1000 F100
;
предварительная обработка
G0 G54 X0 Y61 Z1
Z-36
G1 G42 Y20
G3 J-20
G1 G40 Y25
G2 X17.667 Y17.667 CR=25
;
ROT RPL=45
FOR R0=1 TO 4
G1 X25 Y0
G2 I25
G3 X0 Y25 CR=25
G1
AROT RPL=90
ENDFOR
ROT
G0 Z1
FOR R0=1 TO 4
X61 Y0
Z-36
G1 X30
Y-9
X61
Y9
X30
G0 Z1
X61 Y0
AROT RPL=90
ENDFOR
ROT
G0 Z0
X0 Y0
; PIRAMIDA (ROKR, HH, GRANI, RFR, DZ)
; ROKR - радиус описанной окружности
; HH
- высота пирамиды
; GRANI - количество граней
; RFR
- радиус фрезы
; DZ
- шаг по оси Z
;
PIRAMIDA (20, 36, 3, 5, 3)
; центральная трёхгранная
;
R1=0
FOR R2=4 TO 7
; остальные, начиная с четырехгранной,
; против часовой стрелки
93
AROT RPL=R1+45
ATRANS X50
X0 Y0
PIRAMIDA (20, 36, R2, 5, 3) ; количество граней передается через параметр R2
TRANS
R1=R1+90
ENDFOR
G0 Z50 M5
M30
Результат на рисунке 61.
Рис. 61
94
5.3. Подпрограмма фрезерования полу- и части сферы
Условия:
1. Локальный ноль должен находиться на вершине сферы
2. Фреза должна находиться в локальном нуле.
Рассмотрим рисунок 62.
Рис. 62
Координаты i-ой точки вычисляются по формулам:
Xi=r+Rsin(α), Zi=Rcos(α), где
R – радиус сферы
r – радиус фрезы,
α – текущий угол.
; подпрограмма фрезерования сфер
;
PROC SFERA (REAL R_SF, REAL R_FR, REAL UGOL, REAL DUG) DISPLOF
; принимаемые переменные
; R_SF - радиус сферы
; R_FR - радиус фрезы
; UGOL – половина угла раскрыва
; DUG - шаг изменения угла
;
; дополнительные переменные
;
DEF REAL DX=0
; смещение по оси Х
DEF REAL DZ=0
; смещение по оси Z
DEF REAL UG=0
; текущее значение угла
95
;
G1 X=R_FR
; сдвиг на радиус фрезы
;
WHILE (UG<UGOL)
UG=UG+DUG
DX=R_FR+R_SF*SIN(UG)
DZ=R_SF-R_SF*COS(UG)
G1 X=DX
Z=-DZ
G2 I=-DX
ENDWHILE
G0 Z1
X0
;
RET
Главная программа.
Фрезерование полусферы и части (меньшей) сферы (рис. 63)
Рис. 63
; заготовка 25-X-75, 25-Y-25, Z1=40, Z2=30
T1 D1 M6
M3 S1000 F100
G0 G54 X0 Y0 Z1
G1 Z0
SFERA (25, 5, 90, 2)
; вызов подпрограммы
; 1 параметр - радиус сферы
; 2 - радиус фрезы
; 3 - угол
; 4 - шаг изменения угла
96
TRANS X55 Y0
X0 Y0
ATRANS Z-11.84
G1 Z0
SFERA (20, 5, 70, 2)
TRANS
G1 X81 Y25
Z-25
G1 X28
X30
Y-25
X28
X80
G0 Z50 M5
M30
; подчистка
Результат на рисунке 64.
Рис. 64
Строго говоря, представленные подпрограммы не совсем универсальны,
поскольку в них отсутствует обработка нештатных ситуаций. Включение такой
обработки непомерно увеличило бы объѐм подпрограмм, что затруднило бы
их понимание. Впрочем, при корректном внесении значений переменных приведенные
подпрограммы вполне работоспособны.
97
ЗАКЛЮЧЕНИЕ
Ну вот, пожалуй, и всѐ. Полагаю, что для студентов, которых наши «педагогини»
всѐ ещѐ держат за детей, хотя это пятипудовые парнишки длиной под два метра, и
которые считают, что тангенс это фамилия зарубежного писателя, а Пифагор – позывной
советского разведчика, действовавшего во время Великой отечественной войны на
территории Греции (а может и был такой?), вполне достаточно. Хотелось бы, чтобы
эта книжка принесла какую-нибудь пользу.
Донской, Руднев, июль-август 2014 г.
98
ПРИЛОЖЕНИЕ
Примеры для самостоятельной работы.
Задание. Запрограммировать обработку приведенных деталей. Чем короче УП,
тем лучше.
99
Рис. 65
100
Вырезать из листа фрезой диаметром 6 мм Т-образные элементы.
У нас получилась основная программа в 15 кадров. Причем количество кадров
в УП остаѐтся постоянным независимо от количества горизонтальных и вертикальных
рядов элементов.
101
Рис. 67
102
Рис. 68
103
Рис. 69
104
Рис. 70
105
Рис. 71
106
Рис. 72
107
Рис. 73
Сравните объѐмы УП: программы с параметрами и программы, полученной
c помощью САМ-системы, например, PowerMILL, по модели. Результат, думаю,
будет не в пользу второй.
108
ЛИТЕРАТУРА
1. SINUMERIK 810/840D. Программирование. Руководство для начинающих.
ARINSTEIN.
109