Министерство науки и высшего образования Российской Федерации
ФГАОУ ВО «Севастопольский Государственный Университет»
Институт радиоэлектроники и интеллектуальных технических систем
Кафедра «Радиоэлектронные системы и технологии»
ОТЧЕТ
по лабораторной работе №7
«Исследование характеристик линейных дискретных систем»
по дисциплине
«Цифровая обработка сигналов»
Выполнила: студент гр. РС/с-19-1-о
Мозжеров Д.А.
Защитила с оценкой______
Принял: доцент Тыщук Ю.Н.
Севастополь
2022
7.1. Цель работы
1) Изучение основных характеристик линейных дискретных систем (далее ЛДС).
2) Изучение методов описания ЛДС во временной и частотной областях.
3. Изучение функций MATLAB для анализа ЛДС во временной и частотной областях.
7.2. Выполнение лабораторной работы
7.2.1. Исходные данные
Исходные данные для выполнения лабораторной работы укажем в таблице 7.1.
Таблица 7.1 –– Исходные данные для выполнения лабораторной работы
Вариант
a0
a1
a2
b0
b1
b2
12
1
-0.5570
0.2270
0.4460
-0.8920
0.4460
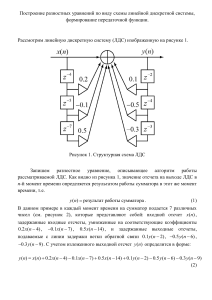
7.2.2. Построение АЧХ и ФЧХ ЛДС
Функция дискретной линейной системы имеет вид:
b 0 b1 z 1 b2 z 2
Н z
a 0 a1 z 1 a 2 z 2
Требуется:
–– построить частотные характеристики заданной ЛДС.
Для этого используем следующий листинг программы:
fd = 1000;
Td = 1/fd;
N1 = 20;
a = [1 -0.5570 0.2270];
b = [0.4460 -0.8920 0.4460];
N = 2000;
[H, w] = freqz(b, a, N);
figure(1)
plot(w/(2*pi), abs(H))
set(gca,'FontName','Arial Cyr','FontSize',10);
title('АЧХ ЛДС')
ylabel('H, В')
xlabel('w, рад/с')
grid on
figure(2)
plot(w/(2*pi), angle(H))
set(gca,'FontName','Arial Cyr','FontSize',10);
title('ФЧХ ЛДС')
ylabel('Phi, рад')
xlabel('w, рад/с')
grid on
Результат работы программы изобразим на рис. 7.1––7.2.
Рис. 7.1 –– АЧХ ЛДС
Рис. 7.2 –– ФЧХ ЛДС
7.2.3. Построение импульсной характеристики ЛДС
Требуется:
–– построить импульсную характеристику заданной ЛДС.
Для этого используем следующий листинг программы:
[h,t] = impz(b,a);
figure(3)
stem(t*Td, abs(h))
set(gca,'FontName','Arial Cyr','FontSize',10);
title('Импульсная характеристика ЛДС')
ylabel('H, В')
xlabel('t, с')
grid on
Результат работы программы изобразим на рис. 7.3.
Рис. 7.3 –– Импульсная характеристика ЛДС
7.2.4. Формирование и фильтрация сигнала x(nTД)
Требуется:
–– сформировать сигнал x(nTД) = cos(ω1nTД) + cos(ω2nTД) + cos(ω3nTД);
–– выполнить фильтрацию во временной и частотной области.
Для этого используем следующий листинг программы:
N1=40;
n = 0:1:N1-1;
f1 = 50;
f2 = 150;
f3 = 400;
x=cos(2*pi*f1*n*Td)+cos(2*pi*f2*n*Td)+cos(2*pi*f3*n*Td);
figure(4)
stem(n*Td,x)
set(gca,'FontName','Arial Cyr','FontSize',10);
title('Сформированный сигнал')
ylabel('A, В')
xlabel('n')
ylim([-4 4])
grid on
Результат работы программы изобразим на рис. 7.4.
Рис. 7.4 –– Сформированный сигнал x(nTД)
Для фильтрации во временной и частотной областях напишем следующий листинг
программы:
y1 = filter(b,a,x);
figure(5)
stem(n*Td,y1)
title('Результат фильтрации во временной области')
grid on
n = N1;
y2 = ifft(fft(x).*fft(b,n)./fft(a,n));
figure(6)
n = 0:1:length(y2)-1;
stem(n*Td, y2)
title('Результат фильтрации в частотной области')
grid on
Результат работы программы изобразим на рис. 7.5––7.6.
Рис. 7.5 –– Результат фильтрации сигнала во временной области
Рис. 7.6 –– Результат фильтрации сигнала в частотной области
7.2.5. Построение графиков выходных процессов
Требуется:
–– построить графики выходных процессов в соответствии с п. 7.2.4 и в одной системе координат.
Для этого используем следующий листинг программы:
X = fft(x);
figure(7)
subplot(3, 1, 1)
stem(n*fd/N1, 2/N1*abs(X))
title('Спектр входного сигнала')
grid on
Y1 = fft(y1);
figure(7)
subplot(3, 1, 2)
stem(n*fd/N1, 2/N1*abs(Y1))
title('Результат фильтрации во временной области')
ylim([0 1.5])
grid on
Y2 = fft(y2);
figure(7)
subplot(3, 1, 3)
stem(n*fd/N1, 2/N1*abs(Y2))
title('Результат фильтрации в частотной области')
ylim([0 1.5])
grid on
Результат работы программы изобразим на рис. 7.7.
Рис. 7.7 –– Графики спектра входного сигнала и результатов фильтрации
7.3. Выводы
В результате выполнения лабораторной работы были построены частотные и временные характеристики ЛДС.
В результате фильтрации нет эффектов растекания спектра, так как частоты бимов
кратны частоте дискретизации, и почти полностью подавляется третья гармоника, что и
требовалось в задании, то есть частоты выбраны верно.