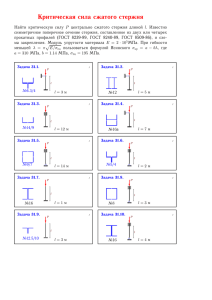
Вариант 8 Задание 1 Задана плоская составная стержневая конструкция, состоящая из двух частей АВ и ВС, связанных между собой шарнирной связью В, показанная на рис. 1.1. Конструкция размещена на опорах А и С. К ней приложены внешние сосредоточенные силы Р = 4 кН, Q = 2,5Р = 10 кН и сосредоточенный внешний момент М = 8 кН∙м. Размер а = 2 м. Требуется найти реакции XA,YA, MA опоры А,XС, опоры С и XВ, YВ связи В. Рис.1.1 Решение: Для определения реакций расчленим конструкцию в шарнире В и рассмотрим равновесие части АВ, на который действуют силы: (Рис. 1.1): реакции XA,YA, MA опоры А и реакции XВ,YВ +2,5Р связи В, а также равновесие части ВС с действующими на нее силами реакциями XВ, YВ связи В, XС опоры С и момента М. Составим уравнения равновесия части АВ: X X A XB 0 A YB 2,5P 0 Y Y M A (1) (2) M A (2,5P YB )a X B a 0 (3) Составим уравнения равновесия части ВС: X X Y Y B M B B XС 0 P0 X С 2a P a M 0 (4) (5) (6) 2 Рис.1.1 5. YB = P = 4 кН 6. XC = -P/2 +M/2a = -4/2 + 8/4 = 0 4. XB = XC = 0 (7) 1. XA = - XC = 0 2. YA = -YB +2,5·P = -4 +2,5·4 = 6 кН 3. MA = (2,5P - YB) · a = 6·2 = 12 кН·м. Модули реакций R A и RB опор А и В определим из формул: RA X A2 Y A2 0 6 2 = 6 кН. RB X B2 YB2 0 4 2 = 4 кН. Результаты расчета сведены в таблицу. Проверка Для проверки правильности решения объединим части АВ и ВС расчетной схемы, показанной на рис. 1.1, относительно связи В вместе. В результате получим расчетную схему, показанную на рис. 1.2 3 Рис.1.2 Составим систему уравнений равновесия (8) для полученной расчетной схемы: X X A XC 0 0 0 ; Y Y P 2,5P 6 4 10 0 ; M M 2,5Pa M 2Pa 12 20 8 16 0. (8) A А A где уравнение моментов записано относительно опоры А. Тождество уравнений нулю при подстановке в них расчетных данных из табл. 3 свидетельствует о правильности решения. Задание 2 Задана нагруженная пространственная стержневая конструкция, размещенная на опорах (рис.2). Оси координат x и y направлены 4 соответственно горизонтально и вертикально в плоскости чертежа этой конструкции, а ось z перпендикулярно к плоскости чертежа. Дано: Р = 4кН, q = 2 кН/м, а= 4 м. Требуется найти реакции ее опор Рис.2 В общем случае систему уравнений равновесия пространственной конструкции, состоящую из трех уравнений проекций и трех уравнений моментов, можно записать в виде: F xi 0 ; F yi 0 ; F zi 0 ; i i i M xo ( Fi ) M xm 0 ; M yo ( Fi ) M ym 0 ; i m i (9) m M ( F zo i ) M zm 0 , i m где F xi , F yi и F zi - проекции внешних сил, действующих на конструкцию, и реакций ее опор на оси координат x, y и z; M xo ( Fi ) Fxihi , M yo ( Fi ) Fyi hi и M zo ( Fi ) Fzi hi - моменты этих сил и реакций относительно осей координат x, y и z в соответствующих плоскостях Оyz, Оxz и Оxy при условии того, что 5 эти плоскости рассматриваются со стороны конца осей координат x, y и z; hi плечи этих проекций сил и проекций реакций относительно какой-либо произвольной точки О в соответствующих плоскостях Оyz, Оxz и Оxy; M xm , M ym и M zm - внешние сосредоточенные моменты, приложенные к конструкции в этих же соответствующих им плоскостях Оyz, Оxz и Оxy. Отбросим от рассматриваемой конструкции ее опоры А, В, С, D и заменим их действие реакциями XD YD, ZD, ZA, ZC и YB. В результате получим расчетную схему, показанную на рис. 2.1. Первоначально направления реакций XD YD, ZD, ZA, ZC и YB выберем положительными. Рис.2.1 Согласно расчетной схеме на рис. 2.1а), конструкция содержит шесть неизвестных реакций XD YD, ZD, ZA, ZC и YB Уравнений равновесия (9) для определения этих реакций тоже шесть, т. е. решаемая задача статически определена. Запишем систему уравнений равновесия (10) этой конструкции по ее расчетной схеме в виде: 1. Х X 2. Y Y D D Q P 0; YB 0 ; 6 3. Z Z 4. M DX D Z A ZC 0 ; (10) Z C a / 2 0 ; 5. M DY Z C a Z A a 0 ; 6. M DZ YB a Pa / 2 0 , где уравнения моментов записаны относительно опоры D, которая выбрана за начало координат системы отсчета Dxyz; Q - внешняя сосредоточенная сила Q qa 2 4 = 8 кН, приложенная посередине участка а, заменяющая внешнюю распределенную нагрузку с интенсивностью q. Из системы уравнений равновесия (10) получим: 6. YB =P/2 = 2 кН; 2. YD = -YB = -2 кН; 4. ZC = 0 кН; 5. ZA = 0 кН; 1. XD = -Q +P = -4 кН; 3. ZD = 0 кН; где номер перед реакцией соответствует номеру уравнения в этой системе, из которого она определена. Отрицательные значения реакций X D и YD характеризует то, что направления этих реакций должны быть изменены на обратные. После повторного расчета этих реакций с измененными направлениями они примут положительные значения ХD = 4 кН и YD =2 кН.(Рис.2.1 б)) Модуль реакций RD опоры D определим по формуле RD X D YD 4 2 2 2 = 4,47 кН 2 2 Результаты расчета сведены в таблицу 7 Проверка Для проверки правильности решения выберем точку О(-а/2,а/4,а/2) , как показано на расчетной схеме, приведенной рис.2.1б. Точка О выбрана так, что в уравнения моментов (9) входят все шесть ранее определенных реакций XD YD, ZD, ZA, ZC и YB из таблицы. Составим уравнения моментов (9) относительно этой точки: M XO Z D a / 4 Z A a / 4 ZC a / 4 0 0 0 0 M УO Z D a / 4 Z A a / 4 ZC a / 4 Q a / 4 P a / 4 X D a / 4 0 0 0 8 4 4 0 M ZO Q a / 4 Pa / 4 YB a / 2 YD a / 2 X D a / 4 8 4 4 4 4 0 Тождество этих уравнений нулю при подстановке в них расчетных данных из табл. свидетельствует о правильности решения. Задание 3 Нагруженный ступенчатый стержень из хрупкого материала с одним свободным, а с другим жестко закрепленным концом работает на центральное растяжение и сжатие, либо только на растяжение или сжатие. Схема варианта нагружения стержня показаны на рис. 3. Здесь же в таблицах приведены соответствующие этим схемам исходные данные. Ось координат x проходит по центральной оси стержня. Требуется: построить эпюры внутренних продольных сил N x , нормальных напряжений x и перемещений u x поперечных сечений стержня; 8 проверить перемещение свободного конца, используя принцип независимости действия сил; проверить стержень на прочность полагая, что стержень изготовлен из хрупкого материала с пределом прочности при растяжении [ p ] 100 МПа и сжатии [ c ] 200 МПа. Рис.3 Решение. Разбиваем брус на участки, границами которых являются поперечные сечения, в которых или приложены силы или изменяется площадь поперечного сечения бруса. Таких участков 4 (рис.1.2). Определяем внутренние продольные усилия N по участкам, используя метод сечений. Начинаем со свободного конца бруса: 1-й участок CD: N1 = 0 кН – участок не нагружен 2-й участок DB: N2 = Р1 = -800 Н – сжатие (11) 3-й участок BE : N3 = Р1 = -800 Н – сжатие 4-й участок EA : N4 =P2 – Р1 =1200 – 800 = 400 Н – сжатие Строим эпюру N (Рис. 1.2). Для построения эпюры нормальных напряжений определяем напряжения на участке по формуле N F , где F– площадь поперечного сечения на участке. Изменение длины участка от действия нагрузки находим по формуле 9 l Тогда 1 1-й участок CD: l1 2-й участок DB: 3 N1 0 Н/мм2 = 0 МПа, 6 F1 50 10 1 l1 E 0 20 = 0 мм 2 10 5 2 l2 E (12) 16 80 = -0,0064 мм 2 105 N3 800 Н/мм2 = -8 МПа, 6 F2 100 10 l3 4-й участок ЕА: E N2 800 Н/мм2 = -16 МПа, F1 50 10 6 2 l2 3-й участок BЕ: l 3 l3 E 8 60 = -0,0024 мм 2 105 N 400 Н/мм2 = 4 МПа, 4 4 6 F2 100 10 l4 4 l4 E 4 40 = 0,0008 мм 2 105 Смещение uA, uE, uB, uD, uC, сечений А, Е,В, D, и C стержня определим как: uA 0 u E u A l4 = 0,0008 мм; u B u E l3 = -0,0016 мм; uD uB l2 = -0,008 мм; uС u В l1 = -0,008 мм; Строим эпюры нормальных напряжений σ и cмещение сечений u (Рис. 3.2). Проверим смещение uC сечения C стержня по принципу независимости действия сил. 10 Рис. 3.2 Рассчитаем uC от действия сил Р1и Р1 отдельно: uС ( P1 ) l DB l BE uС ( P2 ) l AE P1l DB P1l BE 800 80 800 60 0,0088 мм. 5 EFDB EFBE 2 10 50 2 10 5 100 P21l AE 1200 40 0,008 мм. EFAE 2 10 5 100 Тогда uС uС ( P1 ) uС ( P2 ) 0,088 0,008 0,0008 мм. Проверим стержень на прочность. Для этого запишем условие прочности стержня при его растяжении 4 [ p ] (13) и сжатии | 2 | max [ c ] , 11 где | 4 | max и | 2 | max - максимальные значения нормальных напряжений на участках АВ и CD при растяжении и сжатии стержня, которые взяты по модулю. После подстановки из условий прочности (122) имеем: 4 100 МПа; 16 200 МПа. Из полученных неравенств делаем вывод, что при заданных нагрузках P1 , P2 размерах и свойствах материала Е стержня он удовлетворяет условиям прочности. Коэффициент запаса по пределу прочности стержня составляет n [ c ] / | CD | max 200 / 16 12,5 (14) Задание 4 На рис. 4 дана схема нагружения стержня. Двно: l1 = 500 мм, l2 = 200 мм, М1 = 240 Н·м, М2 = -40 Н·м, G = 8·104 МПа, [τ] = 30 МПа, [θ] = град/м, с = dB/d = 0,6. l1 l2 М1 Нм мм 500 М2 200 240 -40 G MПа 8∙104 30 с dB / d град/ м 0,6 0,6 Требуется: найти внутренние крутящие моменты M AB и M BC на участках АВ и ВС стержня; подобрать размеры поперечных сечений стержня (диаметр d стержня и размер h = b стороны его квадрата) для этих участков исходя из условий прочности d AB , d BC и жесткости d AB , d BC , а также принять единый размер d h b их поперечных сечений; найти углы АВ и ВС закручивания участков АВ и ВС стержня и угол С поворота его свободного конца; 12 построить эпюры внутренних крутящих моментов M x и углов x поворота сечений стержня. Рис.4 Решение. Для определения внутреннего крутящего момента M AB составим уравнение равновесия стержня в сечении 1 - 1: М х М АВ М1 М 2 0 , откуда М АВ М 1 М 2 240 40 200 Н∙м. Для определения неизвестного внутреннего крутящего момента M BC составим уравнение равновесия стержня в сечении : М х М ВC М 2 0 , откуда М ВC М 2 40 Н∙м. Подбор диаметров поперечных сечений на участках АВ и ВС осуществим исходя из условия прочности max M max / W , (15) где max и M max максимальное касательное напряжение и максимальный внутренний крутящий момент на рассматриваемом участке стержня; предельно допустимое касательное напряжение. Участок АВ 13 Подставив в (15) M max | M AB | и W для квадратного поперечного сечения участка АВ стержня получим d AB 3 | M AB | 200 3 = 0,31634 м. 0,21 0,21 30 10 6 Участок ВС Подставив в (15) M max | M BC | и W для кольцевого поперечного сечения участка ВС стержня получим d BC 3 16 | M BC | 16 40 = 0,19833 м. 3 4 (1 c ) 3,14(1 0,6 4 ) 30 10 6 Подбор диаметров поперечных сечений на участках АВ и ВС исходя из условия жесткости: max M max /(GJ ) , (16) где max и M max - максимальный относительный угол закручивания и максимальный внутренний крутящий момент на рассматриваемом участке стержня; - предельно допустимый относительный угол закручивания. [θ] = 0,6 град/м = 0,6·π/180 = 0,01 рад/м. Участок АВ Подставив в (16) M max | M AB | и J для квадратного поперечного сечения участка АВ стержня получим d AB 4 180 | M AB || 180 200 4 = 0,1 м. 0,14 G 0,14 3,14 0,01 8 10 4 10 6 Участок ВС 14 Подставив в (16) M max | M BC | и J для кольцевого поперечного сечения участка ВС стержня получим d BC 4 32 180 | M AB || 32 180 40 4 = 0,076 м. 2 4) 2 G (1 c 3,14 0,01 8 10 4 10 6 (1 0,6 4 ) За единый размер для обоих участков примем наибольший из четырех рассчитанных выше d h b d AB = 0,1 м ≈ 100 мм. Рис.4.1 Абсолютные углы закручивания АВ и ВС участков АВ и ВС стержня определим из формул: AB M AB l1 M AB l1 200 0,5 = 0,89·10-4 рад. 4 4 GJ G 0,14d 8 10 10 6 0,14 0,14 15 BC M BC l 2 32M BC l 2 32 40 0,2 = -0,12·10-4 рад. 4 4 4 6 4 4 GJ Gd (1 c ) 8 10 10 3,14 0,1 (1 0,6 ) где в первой формуле J для квадратного поперечного сечения стержня , а во второй - для его кольцевго поперечного сечения . Определим абсолютный угол С закручивания свободного конца стержня: А 0; B A AB = 0,89·10-4 рад. C B BC 0,89 10 4 0,12 10 4 = 0,77·10-4 рад. Результаты расчета сведены в табл. Таблица M AB M BC d AB d BC Нм 200 -40 d AB d BC d АВ 19,8 100 С 10-4 рад мм 31,6 ВС 76 100 0,89 -0,12 0,77 По результатам расчетов строим эпюры внутренних крутящих моментов M x и абсолютных углов x закручивания сечений стержня, которые показаны на рис. 4.1 Задание 7 Расчетная схема плоской составной конструкции примера задания 1 (вар.8) показана на рис. 7. Результаты расчета реакции Y A , M A , ее опор А и С приведены в табл. примера этого же задания: Р = 4 кН, М= 8 кНм ,а = 2 м 16 Рис.7 Требуется построить эпюры внутренних продольных N x и поперечных Q y сил, а также внутренних изгибающих моментов M z в этой конструкции. Решение. Для определения продольных N x и поперечных Q y сил, а также изгибающих моментов M z на участках АВ и ВС рассматриваемой составной конструкции воспользуемся методом сечений. Запишем систему уравнений равновесия стержня на участке АЕ: X X Y Y A A М М Qx 0 ; Nx 0 ; А X Ax 0, где 0 х 12 м . Из этой системы определим: N X YA 6 кН; QX 0 кН; M z1 ( x) M A 12 кН∙м. 17 На участке ЕВ: X X A Nx 0 ; Y Y A Qx 0 ; М М А YA x 0 , где 0 х 2 м . Из этой системы определим: N X 0 кН; QX 6 кН; M z1 ( x) 12 6x кН∙м. Мz(0) = 12 кН∙м. Мz(2) = 0 кН∙м. На участке ВD: X X Y Y Nx 0 ; A Qx 2,5P 0 ; A М М z (2) YA x 0 , где 0 х 2 м . Из этой системы определим: N X 0 кН; QX 4 кН; M z1 ( x) 4 x кН∙м. Мz(0) = 0 кН∙м. Мz(2) = 8 кН∙м. На участке DC: X X Y Y Nx 0 ; A A М М Qx 2,5P 0 ; z (2) M 0 , где 0 х 2 м . Из этой системы определим: N X 4 кН; QX 0 кН; M z1 (2) 8 8 0 кН∙м. Построенные эпюры N x , Q y и M z показаны на рис. 7.1. 18 Рис.7.1 Задание 8 Задана пространственная стержневая конструкция, варианта 8 схемы 8 задания 2. : Р = 4кН, q = 2 кН/м, а = 4 м, Q = qa = 8 кН. Используя исходные данные, расчетную схему и результаты расчета реакций опор этой конструкции, выполненные в задании 2, требуется построить эпюры продольных N x Qx и поперечных Q y , Q z сил, крутящих М кр М x и изгибающих M y , M z моментов в ее стержнях. Рис.8 19 Решение. Для определения продольной N x и поперечных Q y , Qz сил, а также крутящего М кр и изгибающих M y и M z моментов на участках АВ, ВС, СЕ и ЕD стержня рассматриваемой пространственной конструкции воспользуемся методом сечений. В каждом сечении i – i будем отбрасывать наиболее удаленную от опоры А часть конструкции и определять внутренние продольную N x Qxi и поперечные Q y Q yi , Qz Qzi силы, а также внутренние крутящий М кр М xi и изгибающие M y M yi , M z M zi . Участок АВ (Рис.8.1): Запишем систему уравнений равновесия: X N ч Qx1 0 ; Z qx 1 QZ1 0 Рис. 8.1 Y Y B Qy1 0 ; М x11 М x1 0 ; M y1 YB x1 М y1 0 ; 20 М z11 qx12 / 2 М z1 0 , где 0 х1 а . Из этой системы определим: Q x1 0 кН; Q y1 ( x1 ) YB = 2кН; Q1Z ( x ) qa = 8 кН; 1 М x1 0 М y1 ( x1 ) М y1 (0) 0 ; М y ( x ) М y (a) YB a = 8 кНм; 1 1 1 М z1 ( x1 ) М z1 (0) 0 ; М z ( x ) М z (a) qa 2 / 2 = -16 кНм. 1 1 1 Участок ВС (Рис.8.2): Рис.8.2 Запишем систему уравнений равновесия : X Y B Qx 2 0 ; Y Q Q Z Q z2 y2 0; 0; 21 М Qa / 2 М X 2 0 ; x 2 2 M M Y 2 2 Z 2 2 МY 2 0 М Z 2 0 ;, где 0 х а /2, 2 Из этой системы определим: Qx1 N X YB = -2 кН; Q y 2 Q 8 кН; Qz 2 P 6 кН; М x 2 Qa / 2 = -16 кНм; М y 2 ( x2 ) 0 ; M Z 2 ( x2 ) 0 ; Участок СЕ (Рис.8.3): Рис.8.3 Запишем систему уравнений равновесия в этом сечении: X P Q Q x3 Y Y B 0; QY 3 0 ; 22 Z Q 3 M M Y 33 M X3 0; M X3 0; M Y 3 Qa / 2 = 0 ; Z 33 YB a Mz 3 0 , M Z 3 ( x3 ) где 0 х3 а . Из этой системы определим: Qx 3 Q P = 4 кН; Qy3 = -YB = -2 кН; Qz 3 Pq YB 6 кН; M X3 0 M Y 3 Qa / 2 = -16 кНм; M Z 3 YB a = 8кНм; Участок ЕD (Рис.8.4): Рис.8.4 23 Систему уравнений равновесия в этом стержне: ΣX = YD – YB + Qx4 = 0 ΣY = Q – XD + Qy4 = 0 ΣZ = Qz4 = 0 ΣMx4-4 = Qa/2 + Mx4= 0 ΣMy4-4 = Qy4 = 0 ΣMz4-4 = Qz4 = 0 где 0 x4 а / 2 . Из этой системы определим: Qx4 = YB – YD = 0 Qy4 = XD – Q = -4 кН. Qz4 = 0 Mx4 = -Qa/2 = -16 кНм. My4 = 0 Mz4 = 0 Эпюры внутренних усилий в конструкции показаны на рис. 8.5 24 Рис.8.5 25 Список использованной литературы 1. Савелькаев, С.В. Механика. Сопротивление материалов: практикум/С.В. Савелькаев, М.Б. Устюгов, А.И. Совертков; под общ. ред. Савелькаева С.В. – Новосибирск: СГГА, 2011. – 72 с. 2. Голипад Л. И., Совертков А. И. Сборник задач по механике деформируемых тел: метод. разработки. – Новосибирск: НИИГАиК, 1985. – 57 с. 3. Федосеев, В.И. Сопротивление материалов/В.И. Федосеев. М.: Наука,1979. – 560 с. 26