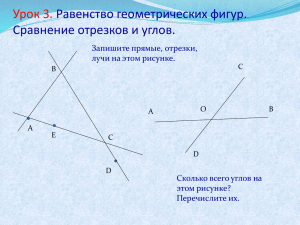
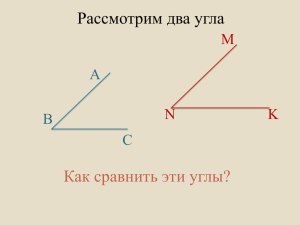
Задачи по теме «Многогранный угол» 1) Чему равна сумма всех плоских углов треугольной пирамиды? 2) Найдите двугранные углы трёхгранного угла, плоские углы которого равны 90°, 90° и a. 3) Все плоские углы трёхгранного угла равны 90°. Найдите углы между биссектрисами плоских углов. 4) В каких пределах может меняться плоский угол трёхгранного угла, если два оставшихся соответственно равны: а) 70 и 100°; б) 130 и 150°? 5) Дан трёхгранный угол. Рассмотрим три плоскости, содержащие грани этого трёхгранного угла. Эти плоскости делят пространство на восемь трёхгранных углов. a) Найдите плоские углы всех образовавшихся трёхгранных углов, если плоские углы исходного трёхгранного угла равны α, и γ. b) Найдите двугранные углы всех образовавшихся трёхгранных углов, если двугранные углы исходного трёхгранного угла равны a, b и g. 6) Через одну точку пространства проведены четыре плоскости, никакие три из которых не имеют общей прямой. На сколько частей делят пространство эти плоскости? Как называются образовавшиеся части пространства? 7) Противоположные рёбра треугольной пирамиды попарно равны. Докажите, что все грани этой пирамиды — равные между собой остроугольные треугольники. 8) A, B, C, D — четыре точки пространства. Известно, что AD =BD = CD, ∠ ADB = 90°, ∠ ADC = 50°, ∠ BDC = 140°. Найдите углы треугольника ABC. 9) Все плоские углы трёхгранного угла равны 60°. Найдите углы, образованные рёбрами этого трёхгранного угла с плоскостями противоположных граней. 10) Вершины двух трёхгранных углов совпадают, при этом рёбра первого из них целиком расположены внутри второго. Докажите, что сумма плоских углов первого трёхгранного угла меньше суммы плоских углов второго. 11) Рассмотрим плоскость p, проходящую через биссектрисы плоских углов AOB и BOC трёхгранного угла OABC. Докажите, что плоскость p пересекает плоскость COA по прямой, перпендикулярной биссектрисе угла COA. 12) Обозначим двугранные и плоские углы трёхгранного угла OABC соответственно через A, B, C и a, b, g (a — двугранный угол при ребре OA, ∠ A = ∠ BOC и т. д.). Возьмём точку O ʹ внутри этого угла и проведём лучи O ʹA ʹ, O ʹB ʹ и O ʹC ʹ, соответственно перпендикулярные граням трёхгранного угла OABC и пересекающие их (или их продолжения). Найдите плоские и двугранные углы трёхгранного угла O ʹA ʹB ʹC ʹ. 13) Все плоские углы трёхгранного угла прямые. Докажите, что любое его сечение есть остроугольный треугольник. 14) У любого ли трёхгранного угла можно провести сечение, являющееся правильным треугольником? 15) Докажите, что в любой треугольной пирамиде найдётся вершина, у которой все плоские углы острые.