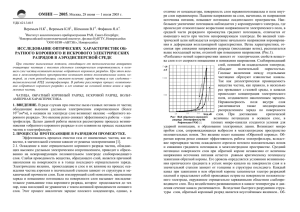
SIMULATION OF BALL MILLS UNDER UNCERTAINTY CONDITIONS The separation of rare and precious metals from ore is associated with its grinding. Ball, rod, semi-autogenous and autogenous mills are used for grinding ore. The mill of the latter type uses only the ore itself as the grinding medium, while in semi-autogenous and ball mills, along with ore, steel balls are used as the grinding medium. Let us consider in more detail the grinding process in a ball mill, where the material to be ground is part of the grinding medium. Changes in the state of ore before and during grinding is a significant factor of uncertainty in the modeling and control of the grinding process. The composition of the ore in terms of particle size and their hardness and distribution in the medium being ground affects the grinding kinetics, which also contributes to the uncertainty. No improvement in the design of the ball mill can solve this problem. In order to reduce the influence of these uncertainties in the control of this process, closed-loop circuits are used [1]. For example, the main controlled parameters of the grinding process are the size of particles at the outlet of the apparatus, and it is not possible to carry out continuous automatic control over the size of particles in the apparatus and the hardness of the grinding medium in the apparatus, which leads to the impossibility of controlling the influence of disturbing influences and, accordingly, to the uncertainty of the dynamics of the process. [2]. Grinding technological schemes can have various configurations. To control the grinding process, block predictive models are often used [3], consisting of separate modules, for example, for the mill itself, cyclone of water and sump [4]. The block principle of creating a model allows you to simulate the process for various configurations of the grinding technological scheme. In this case, the nonlinearity of the technological process and the uncertainties described above are taken into account in the control system. Grinding process control pursues several goals, firstly, to stabilize the system, and secondly, to optimize the technological process [7]. The economic goal consists of several components, each of which contributes to the achievement of the overall economic goal of the grinding process. The components of the economic goal are: • improving the quality of products, which consists in stabilizing the fineness of grinding and minimizing fluctuations in the size of the product; • maximizing productivity; • minimizing the number of steel balls used per ton of product produced; • minimizing energy consumption for each ton of products produced, etc. All these goals are interrelated and require a certain compromise solution, since, for example, productivity cannot be increased to certain values without compromising product quality. The problem of controlling the grinding process is to concider the strong correlation between the variables, long time delays, uncontrolled disturbances, changes in parameters over time, the nonlinearity of the process and the non-optimality of the design of the grinding plant. [5, 6]. This is achieved by introducing uncertainties and deviations from the process into the predictive model. The control system calculates the optimal sequence of controls or generates certain feedback laws that optimize a given objective function. Let's construct a dynamic mathematical model of a ball mill shown in Figure 1. The mill consists of a mill itself, a sump and a cyclone of water. Figure 1. Ball mill for grinding ore. As can be seen from the figure, ore is fed into the mill together with grinding balls, water and a reverse flow of waste from the cyclone of water The crushed ore in the mill is mixed with water, forming a slurry, which is discharged through a sieve with end discharge, which limits the particle size of the discharged slurry. The withdrawn slurry is collected in a sump where it is diluted with water before being pumped into a cyclone for classification. The cyclone of water is designed to separate substandard ore discharged from the sump. The bottom product is returned to the mill for further crushing of the out-of-specification particles. The list of input and output streams is presented in Table 1. WSM OSG SB FWS FCM GCML ZVS PPS Variables of input Water supply to the mill material, prepared for grinding Metal balls fill water sumpf Flow rate of the circulating mixture Output variables general component of the mill loading Cracking size of sump The size of output particle [м3/h] [t/h] [t/h] [м3/h] [м3/h] [-] [м3] [-] To describe the grinding process as shown in Figure 1, you can use a relatively simple nonlinear dynamic model proposed by Le Roux et al. [8]. This model uses the minimum number of refined parameters, but allows obtaining sufficiently accurate corresponding model responses. The model consists of four blocks describing a feeder, an SAG mill with a diverting screen, a sump and a cyclone of water. Table 2 provides a description of the indices for measured costs V and calculated by model X. Table 2: Description of indexes Low index Description X∆− f-feeder; m - mill; h - sump; g - cyclone of water k - stones; including - solid particles; gh - coarse particles; w - balls; c - water i - inflow; o - exit; u - overflow X−∆ X− − ∆ The first index indicates the module under consideration (feeder, mill, sump or cyclone of water), the second indicates which of the six states is taken into account (stones, solids, coarse particles, fine particles, balls, water), and in the case of flow rates, the last subscript shows, whether it is inflow, overflow, or decreased flow. A description of the continuous time mill circuit in state space is shown below. V H H H овм WSM v mw mw VFWS H ms H mw V H H OSG P X mr H ms (1 r ) v mw ms VFSS mill ( ) Ds H ms H mw Ds r X mr X ms V H H P OSG f v mw mf VFFS mill / Ds H ms H mw Ds f H mf H H mr H ms H mb [1 f ( mw Pmax )] mill P H mr OSG H mr к mill ( ) Ds D s к H mr H ms X mb SB Pmill H mb ( ) DB b Ds ( X mr X ms ) DB X mb (1) Vv H mw H mw FCM H mw H sw FWS H ms H mw H mw H ms Vv H mw H ms FCM H ms H ss H ms H mw H mw H ms Vv H mw H mf FCM H mf H sf H ms H m H mw H ms where H mw , H ms , H mf , H mr , H mb are the volume of water, solid particles, fines, rocks and balls in the mill, respectively, H sw , H ss , H sf are the volume of water, solid particles and small particles in the sump, respectively, and Vhw , Vhs , Vhf is the flow of water, solid particles and fines in the cyclone of water, respectively. Since particulate matter is the sum of the fine and coarse ore, only the solids and fines change is calculated, not the coarse ore change. The nomenclature of the model is presented in tables 3. Table3 : Values of circuit parameters and uncertainty Circuit Given Parameter Value Δ Details of circuit f 0.05 50% Fine part in raw product r 0.47 60% Rock part in raw product P 1.0 f 0.01 скор 0.71 su 0.87 C1 0.6 stable C2 0.4 stable C3 4.0 stable C4 4.0 stable P s 0.5 Power change parameter for solids in the mill P 0.5 DB 7.85 Power change parameter for the volume of the filled mill Density of steel balls [t / m3] DS 4.2 Density of the original ore [t / m3] sv 0.62 c 129 5% b 90 6.6% Maximum fraction of solids by volume of grinding at 0 grinding flow Parameter associated with coarse particles [m3 / h] Wear rate of steel [kW * h / t] f 29.5 50% r 7.1 20% v Partial power reduction by partial reduction from the maximum mill speed Partial change in kW / produced fines for a change in the fractional filling of the mill Fraction of the critical speed of the mill 15% Parameter related to solids in the downstream Power required per ton of fines produced [kW * h / t] Abrasion rate of rocks [kW * h / t] P 1662 Rheology factor for maximum mill power input Pmax 0.57 mill 120 Maximum power consumption of the mill motor [kW] Mill capacity [m3] P 0.4 Vv 84 P 0 max max 6000 Filled fraction of mill volume for maximum power consumption Volumetric flow rate for driving force "current volume" Cross time for maximum power consumption The three outputs of the model are the fraction of the mill filled with the GCML loading, the volume of the sump filled with the ZVS loading, and the estimate of the particle size at the outlet of the PPS cyclone of water, which are calculated by the formulas: GCML ( H mw H ms H mf H mb ) / mill ZVS H ss H sw (2) PPS Vhfo Vhso where Vhfo and Vhso are the volumetric flow rate of fine and solid particles at the outlet of the cyclone of water, respectively. The intermediate equations required for (1) for the mill are determined by the equations: 1 H max 0, 1 1 ms s H mw Pmill Pmax 1 P Z x2 2 P P Ps Z x Z r Ps Z r2 ( speed ) P Zx Zr H mw H mf H ms H mb 1 mill Pmax Pmax 1 where is an empirically determined rheological coefficient, Pmill is the power consumption of the mill, Z x is the effect of the charge inside the mill on the power consumption, and Zr is the effect of the rheology of the charge in the mill on the power consumption. The intermediate equations required for (1) and (2) related to the cyclone are determined by the equations С С FCM 3 H sf 4 FCM(Hss - Hsf ) H ss 1 1 Vhfc 1 C1 exp Hsw Hss С ( H H ) H c 2 sw ss ss V H ss exp hfc Fu 0.6 0.6 H sw H ss su c H sw (Vhfc Fu Vhfc ) Vhfw Fu H sw Fu H sf H sf Vhfo H sf (Vhfc Fu Vhfc ) Fu H sw Fu H sf H sf Vhso Vhfc H sf (Vhfc Fu Vhfc ) Fu H sw Fu H sf H sf Vhso Vsfs Vhso Vhfo Vsff Vhfo where the flow rate of water, solid particles, coarse particles and fines in the bottom flow of the cyclone of water have to be determined in sequence by Vhfw , Vhso , Vhfc and Vhfo , the flow indication of solid and fine particles at the outlet from the sump have to be determined by Vsfs and Vsff , in sequence, and Fu is the part of solid particles in the bottom stream cyclone of water. Table 4: Duty point of the grinding circuit Variable unreal Min Max Unit of measurement Input data FCM 300 100 350 м3/h WSM 40 0 60 м3/h SB 5.69 0 10 t/h OSG 65.2 0 100 t/h FWS 140.5 0 400 м3/h 0.25 0.45 particle Output data GCML 0.34 ZVS 5.99 1 8 м3 PPS 0.67 0.5 0.8 Particle Table 5: Initial states of mill and settler Condition value Unit of measurement Mill state H mw 4.85 м3 H ms 4.90 м3 H mf 1.09 м3 H mr 1.82 м3 H mb 8.51 м3 Sump states H sw 4.11 м3 H ss 1.88 м3 H sf 0.42 м3 In summary, it is clear that shifts in the composition of the ore and its hardness are the main sources of uncertainties that have to be faced in modeling, especially when the ore comes from different deposits. A raise in ore hardness is modeled by a growth in the capacity required to produce a ton of product ( f ) by 50% at a time of 10 minutes. The shift in the composition of the ore is modeled by a raise in the share of raw materials ( r ) by 50% in a time of 100 minutes. PSE is controlled by changing the section of the cyclone. The section of the cyclone of water changes through the SFF [Figure. 2 (b)] and the loading density of the cyclone of waters (SFD). SFD [Figure. 2 (b)] can be changed by changing the density of the mill discharge in relation to the MIW to MSF [Figure 2 (b)], etc. To ensure the effective operation of the cyclone, the control system must control the SFD, PSE and the sump level (US) for which it is equipped with three degrees of freedom [Figure. 2 (a)]. The PSE and mill load are maintained at the desired levels of 80% and 45%, respectively, in a robust nonlinear model predictive control (RNMPC) [Figure. 2 (a)] regardless of active disturbances. Figure. 2 (b) shows a slight decrease in the average MFS due to the increased hardness of the ore. Differences in SFW may be due to different hardness of the ore, which affects the residence time of the ore inside the mill. Large variations in the pickup are needed to control the device of sound waves in order to minimize the density of the suspension in the sump. In fig. 2 (a) additionally shows product performance, slurry rheology within the mill, and mill power input. The rheology factor depends on the water and solids inside the mill, as shown in (6). Rice. 2. Controlled variables, control variables and other important variables. Dashed lines indicate constraints on the variable, and vertical dashed lines indicate the onset of disturbing events. To increase the throughput, the RNMPC controls the MIW and MFS by maintaining the optimal conditions for destruction inside the mill, which are achieved at the optimal value of the rheology coefficient equal to 0.51. The control system compensates for the violation of the hardness of the original ore due to an increase in MIW in comparison with MFS. An increase in the MPF of the relative MFS goes with to an raise in the rheology factor and, as a result, leads to a decrease in the power of the mill. RNMPC increases SB [Figure. 2 (b)] to compensate for the higher rheological factor. References 1. I. K. Craig, I. M. MacLeod, Specification framework for robust control of a runof-mine ore milling circuit, Control Eng. Practice 3 (1995) 621 – 630. 2. D. Wei and I. K. Craig, “Grinding mill circuits—A survey of control and economic concerns,” Int. J. Mineral Process., vol. 90, no. 1–4, pp. 56–66, 2009. 3. M. Ramasamy, S. S. Narayanan, and C. D. P. Rao, “Control of ball mill grinding circuit using model predictive control scheme,” J. Process Control, vol. 15, no. 3, pp. 273–283, 2005. 4. R. K. Rajamani and J. A. Herbst, “Optimal control of a ball mill grinding circuit. I. Grinding circuit modeling and dynamic simulation,” Chem. Eng. Sci., vol. 46, no. 3, pp. 861–870, 1991. 5. P. Mhaskar and A. B. Kennedy, “Robust model predictive control of nonlinear process systems: Handling rate constraints,” Chem. Eng. Sci., vol. 63, no. 2, pp. 366–375, 2008. 6. M. Lazar, D. M. de la Pena, W. P. M. H. Heemels, and T. Alamo, “On input-tostate stability of min-max nonlinear model predictive control,” Syst. Control Lett., vol. 57, no. 1, pp. 39–48, 2008. 7. 8. A. Remes, J. Aaltonen, H. Koivo, Grinding circuit modeling and simulation of particle size control at Siilinj¨arvi concentrator, Int. J. Mineral Processing 96 (2010) 70 – 78. 30. J. D. le Roux, I. K. Craig, D. G. Hulbert, A. L. Hinde, Analysis and validation of a run-of-mine ore grinding mill circuit model for process control, Minerals Eng. 43-44 (2013) 121 – 134.