Федеральное агентство по образованию
Уральский государственный технический университет – УПИ
имени первого Президента России Б.Н.Ельцина
О.В. Рябухин
ВЗАИМОДЕЙСВТИЕ ИЗЛУЧЕНИЯ
С ВЕЩЕСТВОМ
Конспект лекций
Печатается по решению редакционно-издательского совета
УГТУ–УПИ от 28.02.2008
Екатеринбург
УГТУ–УПИ
2009
УДК 539.17(075.8)
ББК 22.38 я73
Р15
Рябухин О.В.
Р15 Взаимодействие излучения с веществом: Конспект лекций /
О.В. Рябухин. Екатеринбург : УГТУ – УПИ, 2009. Ч. II. 49 с.
ISBN
Материал предназначен для студентов, специализирующихся в
области экспериментальной физики, в частности для студентов
специальностей 140306 – Электроника и автоматика физических
установок, 140307 – Радиационная безопасность человека и
окружающей среды, 200402 – Инженерное дело в медикобиологической практике и направления подготовки 200400 –
Биомедицинская инженерия. Является продолжением первой и
второй части учебного пособия по ядерной физике и содержит
материал о процессах, протекающих при движении заряженных
частиц и гамма-квантов в средах, исключая ядерные взаимодействия.
Нумерация глав во всех частях сквозная.
Библиогр.: 3 назв. Табл. 1. Рис. 24.
УДК 539.17(075.8)
ББК 22.38 я73
УГТУ – УПИ, 2009
ISBN
2
ОГЛАВЛЕНИЕ
6. ВЗАИМОДЕЙСТВИЕ ИЗЛУЧЕНИЯ С ВЕЩЕСТВОМ…4
6.1. Виды и источники излучений .................................................................. 5
6.2. Взаимодействие заряженных частиц с веществом................................ 6
6.2.1 Формула Бете-Блоха (Бора)............................................................... 6
6.2.2. δ - электроны, первичная и полная ионизация .............................. 10
6.2.3. Зависимость ионизационных потерь от среды............................ 11
6.2.4 Пробег. Связь пробега с энергией частицы.................................... 14
6.2.5. Упругое рассеяние заряженных частиц ........................................ 17
6.2.6. Многократное рассеяние заряженных частиц ............................ 20
6.2.7 Особенности взаимодействия электронов с веществом ............. 22
6.2.8. Радиационное торможение заряженных частиц в среде ........... 26
6.2.9. Излучение Вавилова-Черенкова....................................................... 30
6.2.10. Переходное излучение .................................................................... 34
6.2.11. Синхротронное излучение ............................................................. 37
6.3. Взаимодействие гамма – излучения с веществом ............................... 41
6.3.1. Фотоэффект .................................................................................... 41
6.3.2. Комптоновский эффект ................................................................. 44
6.3.3. Эффект образования пар ................................................................ 48
6.3.4. Ослабление гамма-излучения в веществе ...................................... 50
3
6. ВЗАИМОДЕЙСТВИЕ ИЗЛУЧЕНИЯ С ВЕЩЕСТВОМ
В настоящий момент изучено большое количество эффектов,
протекающих под воздействием излучения в веществе. Они достаточно
разнообразны, но во многом связаны друг с другом. В данной главе будут
рассмотрены основные процессы, протекающие при взаимодействии
излучения с веществом. Наличие данных процессов предоставляет две
основные возможности: 1) зарегистрировать излучение и 2) изменять
различные физические свойства облучаемой среды.
Все
виды
рассматриваемых
фундаментальным
типам
эффектов
взаимодействия.
относятся
Сильное
к
трем
взаимодействие
обуславливает быстрые процессы, протекающие под воздействием
ядерных сил за времена порядка 10-23÷10-22 с и имеющие величину сечения
взаимодействия 10-27÷10-24 см2 (ядерные реакции, резонансное ядерное
рассеяние, распад резонансов).
Электромагнитное
взаимодействие
обуславливает
процессы
взаимодействия заряженных частиц и гамма – излучения с веществом на
расстояниях более, чем 10-12 см. Характерные времена составляют
величину
порядка
10-19 с
(кулоновское
рассеяние,
радиационное
торможение, фотоэффект и др.).
Слабое
взаимодействие
обуславливает
специфический
процесс
взаимодействия нуклонов ядра с окружающим электрон-нейтронным
полем, в результате чего поглощаются, либо возникают электроны,
нейтрино и их античастицы. Характерные времена составляют величину
порядка 10-13 с. Непосредственное взаимодействие излучения с веществом
посредством слабого взаимодействия может происходить при захвате
средой нейтрино и антинейтрино, однако сечения данных процессов
весьма малы (10-43 см2).
4
6.1. Виды и источники излучений
Исходя из материала, представленного в предыдущих главах можно
выделить излучения, содержащие:
• заряженные частицы (β – частицы, р – протоны, α – частицы,
тяжелые ионы, кластеры);
• нейтроны;
• гамма-кванты различного энергетического диапазона.
Основными способами получения излучений являются:
• Процессы
радиоактивного
распада
ядер.
Наиболее
распространенными в этом случае являются β - излучение, ввиду малости
энергии, необходимой для образования данной частицы, и γ - излучение,
являющееся
сопутствующим
для
большинства
распадов
ядер
с
испусканием корпускулярного излучения.
• Ядерные взаимодействия (реакции). Основные виды излучений –
корпускулярное (нейтроны, протоны, альфа – частицы, тяжелые ионы) и
сопутствующее γ - излучение, образующееся при переходе ядер из
возбужденного в более низкоэнергетичное, либо основное состояния. При
прочих равных условиях наиболее вероятно испускание нейтронов ввиду
меньшей энергии связи данного нуклона в ядре и отсутствия кулоновского
барьера.
• Ускорение заряженных частиц. Излучение, полученное данным
способом, отличается от предыдущих, выделенным направлением и
большим варьируемым диапазоном энергий ускоренных частиц.
В качестве источников излучения на основе представленных
процессов используются радиоактивные изотопы различных химических
элементов и физические установки, реализующие ядерные взаимодействия
и ускорение заряженных частиц, используемые в промышленных,
5
научных, медицинских и других целях (например, ядерные реакторы,
нейтронные генераторы, циклотроны, синхротроны и др.).
6.2. Взаимодействие заряженных частиц с веществом
6.2.1. Формула Бете-Блоха (Бора)
Заряженная частица, двигаясь в веществе, испытывает множественные
столкновения, что приводит к уменьшению ее кинетической энергии. С
учетом того, что размеры ядра (10-12 см) существенно меньше размеров
атомов
(10-8 см),
наиболее
вероятно
столкновение
с
атомными
электронами, нежели с ядрами. Поэтому, одним из основных механизмов
потерь энергии заряженной частицы в веществе являются столкновения с
электронной
составляющей
атома,
в
результате
чего
происходит
ионизация и возбуждение атомов среды (т.е. изменение внутреннего
состояния атома).
Пусть частица с зарядом ze , массой m и скоростью v движется мимо
свободного электрона me с параметром удара (прицельным параметром)
ρ (рис. 6.1). В первом приближении электрон за счет кулоновского
взаимодействия получит импульс в направлении, перпендикулярном
направлению движения заряженной частицы:
∆p = ∫ F ⋅ dt.
(6.1)
Если принять, что эффективная
me
длина
z ⋅e
взаимодействия
величину
v
х
2ρ
Рис. 6.1
2ρ ,
то
это
составляет
расстояние
частица проходит за время ∆ t = 2 ρ / v .
На этом участке сила кулоновского
взаимодействия
6
равна
F = z ⋅ e2 / ρ 2 ,
следовательно:
∆p = F ⋅ ∆t =
2 ⋅ z ⋅ e2 ⋅ ρ 2 ⋅ z ⋅ e2
=
,
ρ2 ⋅v
ρ ⋅v
(6.2)
а кинетическая энергия, которую приобретает свободный электрон:
∆p 2
2 ⋅ z 2 ⋅ e4
∆T =
=
.
2 ⋅ me me ⋅ ρ 2 ⋅ v 2
(6.3)
Такую же энергию теряет и заряженная частица.
Пусть частица прошла слой вещества
толщиной
электронов
dx ,
в
равна
котором
ne .
dx
концентрация
Тогда,
ρ
число
электронов, с которыми провзаимодействует
частица ze с параметром удара из интервала
dρ
[ ρ , ρ + dρ ] (рис. 6.2), равно:
Рис. 6.2
dN = ne ⋅ 2 ⋅ π ⋅ ρ ⋅ dρ ⋅ dx.
(6.4)
В результате взаимодействия с атомными электронами частица z ⋅ e
потеряет энергию:
2 ⋅ z 2 ⋅ e 4 ⋅ ne ⋅ 2 ⋅ π ⋅ ρ ⋅ dρ ⋅ dx 4 ⋅ π ⋅ z 2 ⋅ e 4 ⋅ ne dρ
− dT = ∆T ⋅ dN =
=
⋅
⋅ dx.
me ⋅ ρ 2 ⋅ v 2
me ⋅ v 2
ρ
(6.5)
Знак «–» обозначает потерю энергии налетающей частиц. Интегрируя
выражение (6.5) по всем возможным значениям параметра удара ρ и,
принимая во внимание, что концентрация атомов в среде равна n = ne / Z ,
где Z порядковый номер вещества, получим потери энергии заряженной
частицы ze на единицу длины в среде с зарядом Z :
ρ
dT 4 ⋅ π ⋅ z 2 ⋅ Z ⋅ e 4 ⋅ n max dρ 4 ⋅ π ⋅ z 2 ⋅ Z ⋅ e 4 ⋅ n
ρ max
−
=
⋅
=
⋅
ln
∫ ρ
dx
me ⋅ v 2
me ⋅ v 2
ρ min (6.6)
ρ min
7
Известно, что максимальная энергия, которая может быть передана
тяжелой частицей электрону, при v << c равна ∆Tmax = 2 ⋅ me v 2 , приравнивая
это значение к выражению (6.3) найдем
z ⋅ e2
2 ⋅ z 2 ⋅ e4
=
,
me ⋅ v 2 ⋅ 2 ⋅ me ⋅ v 2 me ⋅ v 2
ρ min =
(6.7)
ρ max определяется расстоянием при котором переданная электрону
энергия будет сравнима с потенциалом ионизации I
атома среды.
Приравнивая средний потенциал ионизации к ∆T из (6.3), получим:
ρ max
2 ⋅ z 2 ⋅ e4
2
2
=
=
⋅
z
e
,
me ⋅ v 2 ⋅ I
me ⋅ v 2 ⋅ I
(6.8)
таким образом, найдем отношение
2 ⋅ me ⋅ v 2
ρ max
=
.
ρ min
I
Подставив
(6.9)
в
(6.6)
получим
окончательное
(6.9)
выражение
для
ионизационных потерь в первом приближении:
2 ⋅ me ⋅ v 2
dT 4 ⋅ π ⋅ z 2 ⋅ e 4 ⋅ n
.
−
=
⋅ Z ⋅ ln
I
dx
me ⋅ v 2
(6.10)
Формула (6.10) выведена с помощью классических рассуждений и
достаточно грубо описывает потери энергии налетающей заряженной
частицы в веществе. Более точный расчет с использованием законов
квантовой механики позволяет получить следующее выражение (формула
Бете - Блоха):
2 ⋅ me ⋅ v 2
dT 4 ⋅ π ⋅ z 2 ⋅ e 4 ⋅ n
2
−
=
⋅
Z
⋅
ln
−
β
−
δ
−
U
I (1 − β 2 )
,
dx
me ⋅ v 2
8
(6.11)
где β =
v
- отношение скорости заряженной частицы к скорости света,
c
δ-
поправка на коэффициент плотности среды, U – поправка на энергию связи
электронов на К – и L – оболочках атома среды. Необходимость учета
взаимодействия частицы с электронами внутренних оболочек атома
возникает при относительно низких значениях энергии движущейся в
среде частицы, когда энергией связи нельзя пренебречь. С ростом
порядкового номера Z среды влияние данной поправки на ионизационные
потери энергии заряженных частиц возрастает.
dT
Величину − часто называют тормозной способностью вещества.
dx
Наиболее используемой единицей измерения тормозной способности или
эВ
.
см
потерь энергии заряженной частицы является
Основной физический вывод из формулы (6.10) заключается в том,
что потери энергии заряженной частицы на ионизацию атомов среды
пропорциональны
квадрату
заряда
(z )
2
налетающей
частицы,
концентрации электронов среды ( ne = nZ , n – концентрация атомов или
ядер среды), некоторой функции от скорости ( ϕ (v) ) и не зависят от массы
налетающей частицы.
dT
2
−
∼ z nZϕ (v).
dx
(6.12)
На рис. 6.3 показана типичная экспериментальная зависимость
ионизационных потерь от энергии Т этой частицы. Особенностью
зависимости является то, что при малых энергиях ее значения не
совпадают с экспериментальными в силу того, что формула (6.11) не
учитывает появляющихся процессов перезарядки и взаимодействия ионов
с электронами различных оболочек. В области применимости формулы,
исходя из (6.11) и экспериментальной зависимости следует, что с ростом
9
скорости v налетающей частицы
dE
dx
(при
ионизационные
v << c )
dT
1
потери − падают как
,
затем,
dx
при
T
T = mc 2 достигают
минимума и далее медленно
растут, выходя на плато ( v ≈ c ).
T=mc2
Ограничение логарифмического
T
dT
−
dx
роста
Рис. 6.3
связано
с
поляризацией атомов среды вблизи траектории движения частицы. Данный
эффект
приводит
к
уменьшению
величины
и
радиуса
действия
электромагнитного поля. В выражении (6.11) эффект поляризации
описывается членом δ, пропорциональным концентрации электронов. При
T
=1÷100 МэВ/нуклон величиной δ можно пренебречь.
A
6.2.2. δ - электроны, первичная и полная ионизация
Заряженная частица, при прохождении через вещество, теряет
основную часть энергии на возбуждение и ионизацию атомов среды. В
большинстве
случаев
это
приводит
к
обладающих
кинетической
энергией,
не
образованию
превышающей
электронов,
потенциал
ионизации в данном веществе. В меньшей степени образуются быстрые (δ)
электроны, обладающие энергией, достаточной для ионизации атомов
данной среды. Образование как медленных, так и быстрых электронов
является первичной ионизацией среды заряженной частицей.
В последующем, δ-электроны при взаимодействии со средой, также
возбуждают и ионизуют атомы. Этот процесс называется вторичной
ионизацией.
10
Таким образом, полная ионизация вещества при взаимодействии с
заряженными частицами складывается из процессов первичной и
вторичной ионизации.
Поскольку энергия δ - электронов велика по сравнению с потенциалом
ионизации атомов данного вещества ( Tδ >>I), то процесс их образования
можно рассматривать аналогично процессу рассеяния ионов на свободных
электронах. Диапазон углов вылета δ - электронов будет заключен в
пределах 0 ≤ ψ ≤ 90 , а энергия будет изменяться согласно соотношению:
Tδ =
4me M
T cos 2 ψ ,
2
(me + M )
(6.13)
где Т, М – соответственно кинетическая энергия и масса налетающего
иона. Анализ данной формулы показывает, что наибольшее значение
энергия δ - электронов Tδ будет принимать при угле вылета ψ=0, а
наименьшее – при угле ψ=90°. Максимальной энергией Tδ будут обладать
электроны, образованные при взаимодействии протонов со средой. В
результате чего Tδ max при угле ψ=0 примет значение:
Tδmax =
4me M p
(me + M p )
2
T≈
4me
T.
Mp
(6.14)
Изучение спектров δ - электронов с помощью (6.13) позволяет грубо
оценивать энергию ионизирующей частицы. Например, наличие вдоль
трека протона δ - следов позволяет говорить, что минимальная энергия
протонов в этом случае равняется T p = 460Tδ .
6.2.3. Зависимость ионизационных потерь от среды
Исходя из того, что ионизационные потери заряженной частицы
несложно зависят от параметров движения частиц и характеристик самого
11
вещества, то легко осуществить перерасчет ионизационных потерь частиц
на другие частицы и среды.
Предположим, что в одной и той же среде ( ne - остается неизменной)
движутся две частицы с одинаковым зарядом Z (протон и дейтон). Тогда,
при совпадении скоростей обе частицы в одном и том же веществе будут
иметь одинаковые ионизационные потери (исходя из анализа (6.12)
очевидно, что правые части данного выражения для обеих частиц будут
идентичными):
dT
dTd
= p
.
dx V =V0 dx V =V0
(6.15)
Однако, при одинаковых скоростях, данные частицы будут иметь
различные кинетические энергии, поскольку их массы отличны друг от
друга в два раза и T p / Td = 1 / 2 , следовательно
dT
dTd
.
= p
T
dx
dx
T =T0
T = 0
(6.16)
2
Если взять частицу с большим зарядовым числом, чем z=1, то
необходимо учесть, что такая частица будет иметь ионизационные потери
в z 2 раз большие ионизационные потери по отношению к частице с z=1.
Например, если сравнить ионизационные потери α - частицы и протона
движущихся с одинаковой скоростью в одной и той же среде, то (согласно
6.12):
dTα
dx V =V0 zα2
dT
dT
.
= 2 =4 ⇒ α
= 4 p
=
V
V
=
V
V
(6.17)
0
zp
dx
dx
dTp
0
T = T0
T = T0 / 4
dx V =V0
Перерасчет ионизационных потерь для другой среды тоже не является
сложным, поскольку концентрация атомов остается примерно постоянной
12
для различных сред, и ионизационные потери для одних и тех же частиц в
различных средах (находящихся в одинаковом агрегатном состоянии)
будут зависеть от соотношения порядковых номеров атомов этих сред.
Например, при прочих равных условиях ионизационные потери протонов в
свинце будут примерно в 6 раз больше, чем в алюминии.
dTp
dT
Z dT
= Pb p ≈ 6 p .
dx Pb Z Al dx Al
dx Al
(6.18)
Видно, что при переходе от одной среды к другой происходит сильное
изменение величины ионизационных потерь энергии взаимодействующей
частицы, поэтому, для уменьшения данных различий линейную величину
ионизационных потерь в данной среде нормируют на плотность этой
среды
и
вводят величину удельных
ионизационных
потерь
dT
,
dξ
отнесенную к единице поверхностной плотности ξ = ρ x . Тогда:
dT dT dx dT 1
.
=
=
dξ dx dξ dx ρ
Величину
dT
dξ
(6.19)
также называют массовой тормозной способностью
вещества и измеряют в массовых единицах
эВ ⋅ см 2 кэВ ⋅ мм 2
,
.
г
мг
Поскольку плотность вещества пропорциональна порядковому номеру
вещества
ρ ∼Z
и
ионизационные
потери
заряженной
частицы
dT
пропорциональны порядковому номеру атома вещества ∼Z, то
dx
величина
dT 1
будет не сильно отличаться для всех сред в одинаковом
dx ρ
агрегатном состоянии, и более удобна для проведения теоретических
расчетов.
13
В качестве примера в табл. 6.1. приведены значения массовой
тормозной способности алюминия, свинца и воздуха для протонов
различных энергий.
Таблица 6.1
T p , МэВ
1
10
100
Более 1000
dT
МэВ ⋅ см 2
,
г
dξ Al
dT
dξ
МэВ ⋅ см 2
,
г
Pb
173,0
34,0
5,7
1,7
МэВ ⋅ см 2
dT
,
г
dξ воздух
62,0
18,0
3,6
1,5
300,0
50,0
7,5
2,3
Из таблицы видно, что массовая тормозная способность алюминия и
свинца отличается чуть менее, чем в три раза, тогда как для линейных
потерь это соотношение равно шести (6.18).
Данные для потерь в воздухе приведены для того, чтобы показать
влияние агрегатного состояния среды на различие тормозных способности
, особенно при высоких энергиях заряженных частиц.
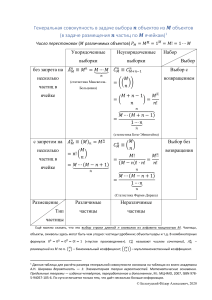
6.2.4 Пробег. Связь пробега с энергией частицы
Как видно из выражения (6.11) величина ионизационных потерь
частицы с зарядом z e для определенной среды является функцией
скорости или кинетической энергии Т:
−
dT
= ϕ (T ).
dx
(6.20)
Выразив данное соотношение в виде:
dx = −
dT
,
ϕ (T )
(6.21)
и проинтегрировав по значениям Т, можно получить уравнение,
определяющее полный пробег частицы в данной среде:
14
X =
T0
dT
∫ ϕ (T ) ,
(6.22)
0
где Т 0 – кинетическая энергия частиц на входе в среду. Соотношение,
аналогичное (6.22) можно получить, выражая ионизационные потери
энергии и через скорость. Согласно (6.12):
dT 2
−
= z nZϕ (v).
dx
(6.23)
С другой стороны, используя соотношения для полной энергии частицы
E=
m0 c 2
1− β
2
и E = m0 c 2 + T , найдем:
dE dE dv
m0
dv
dT d
2
=
=−
.
−
= ( E − m0c ) =
(1 − β 2 )3 / 2 dx
dx dv dx
dx dx
(6.24)
Сравнив (6.24) и (6.23) получим:
z 2 nZϕ (v) = −
m0
(1 − β 2 )3 / 2
dv
,
dx
(6.25)
откуда, интегрируя от v 0 до 0, получим пробег, равный:
v
m0 0
v dv
m0
X= 2
=
Φ (v).
2 3/ 2
2
∫
z Z n 0 ϕ (v)(1 − β )
z Zn
(6.26)
Таким образом, переменные в уравнении (6.26) характеризующие
среду и движение частицы в среде разделились и в первом приближении
можно считать, что функция Φ (v) не зависит от параметров среды. Тогда
для двух различных типов частиц (1 и 2), имеющих равные скорости и
движущихся в различных средах (1 и 2), можно найти приближенное
соотношение пробегов этих частиц в данных средах:
m1 z 22 Z 2 n2
X1 =
X 2.
2
m2 z1 Z1 n1
15
(6.27)
Исходя из (6.27) можно без затруднений вычислить приближенный
пробег для разных частиц в одной и той же среде, либо пробег одной и той
же частицы, но в различных средах. Например, зная пробег протонов в
воздухе X 2 , можно получить пробег этих же частиц в алюминии X 1 ,
используя соотношение:
X1 =
Z 2 n2
X 2.
Z1 n1
(6.30)
С учетом того, что пробег заряженной частицы в среде зависит от
ионизационных потерь энергии, а последние могут измеряться в массовых
единицах, то для пробега также вводят массовую единицу измерения г/см2.
Если уравнение (6.26) преобразовать с учетом М – массы атома среды, то
получим:
X=
m0 M
m0 M
(
)
v
Φ
=
Φ (v),
z 2Z ρ
z 2Z n M
(6.31)
или перенося ρ в левую часть уравнения:
R = Xρ =
m0 M
Φ (v).
z 2Z
[R] = [Xρ ] = см ⋅
г г
. (6.32)
=
см3 см 2
Направление движения тяжелой заряженной частицы в среде (когда
основным механизмом потерь энергии является ионизация и возбуждение)
с
N
течением
времени
меняется
очень слабо, поскольку масса
заряженной
частицы
больше
массы
электронов,
и
в
много
атомных
силу
закона
сохранения импульса изменение
Рис. 6.4
Rэфф x
∆ p для заряженной частицы не
велико. Поэтому практически все
заряженные частицы движутся в среде прямолинейно, и лишь по
16
достижении величины эффективного пробега их число резко уменьшается
(рис. 6.4). В результате этого на глубине равной величине R эфф может
сформироваться слой имплантированных частиц.
Кроме этого, множество экспериментальных исследований показало,
что зависимость ионизационных потерь энергии заряженной частицы от
энергии этой частицы является не сложной. Поэтому, пробег заряженных
частиц в среде можно выразить в виде эмпирических зависимостей,
отражающих характер движения ионов того или иного энергетического
диапазона в данной среде. Так, например, связь между пробегом и
энергией для альфа-частиц в воздухе можно задать соотношением:
Rα = 0,318 Tα3 / 2 см, 4 ≤ Tα ≤ 7 МэВ.
(6.33)
Для частиц с большей энергией (до 200 МэВ) эмпирическое уравнение
примет вид:
Rα = (Tα / 37,2)1,8 м.
(6.34)
Согласно (6.27) можно пересчитать (6.34) для протонов с учетом, того, что
кинетическая энергия протонов T p =
mp
mα
Tα :
R p = (Tp / 9,3)1,8 м.
(6.35)
6.2.5. Упругое рассеяние заряженных частиц
Несмотря на то, что ионизационные потери энергии частицы,
движущейся в веществе, являются основными, немаловажное значение
имеет и взаимодействие с ядрами атомов. В случае, когда энергия
заряженной частицы не превышает энергии кулоновского барьера за счет
электромагнитного
взаимодействия
возможно
упругое
рассеяние
заряженных частиц на ядрах атома. В этом случае внутреннее состояние
взаимодействующих
частиц
не
изменяется,
перераспределение их энергии и импульса.
17
а
происходит
Предположим, что поток заряженных частиц (N) с зарядом z e и
кинетической энергией Т падает на ядро с зарядом Z e , занимающее объем
1 см3, с параметром удара в диапазоне (ρ, ρ +dρ) (рис.6.5). Вероятность
рассеяния
частицы
в
диапазон
углов
дифференциальным сечением рассеяния
(θ,
dσ
,
dΩ
θ +dθ)
где
определяется
d 2 Ω = sin θ dθ dϕ -
телесный угол.
θ
dΩ
dθ
z1e
dϕ
ρ
Ze
ϕ
θ
z1e
Ze
dρ
Рис. 6.5
Число рассеянных частиц на ядре
z 2 e , попавших в телесный угол dΩ
можно определить как:
dN
dσ
= N ⋅ n⋅ x ⋅
,
dΩ
dΩ
(6.36)
где n=1 см-3 – концентрация ядер, х=1 см – толщина мишени. Число
рассеянных
частиц
dN,
выбывших
из
первоначального
потока,
определяется параметром удара:
dN = −2π N ρ dρ .
(6.37)
Таким образом, подставляя (6.37) в (6.36) для дифференциального сечения
рассеяния получаем:
1 N 2π ρ dρ
ρ dρ
dσ
.
=
=−
dΩ
N 2π sin θ dθ sin θ dθ
Для параметра удара известно выражение:
18
(6.38)
ρ=
где rmin
1
rmin
dρ
r
,
⇒
= − min
2 tg (θ /2)
4 sin 2 (θ /2)
dθ
z Z e2
=
T
(6.39)
- минимальное расстояние, на которое налетающая
частица сближается с ядром. Тогда:
2
2
z Z e2
dσ
rmin rmin
rmin
1
1
1
1
=
=
=
.
dΩ 2 tg(θ/2) 4 sin 2 (θ / 2) sin θ 16 sin 4 θ 4T sin 4 θ (6.40)
2
2
Уравнение (6.40) называется формулой Резерфорда (получена в 1911 г.),
которая выведена в предположении о том, что заряженная частица
рассеивается на бесконечно большом по массе ядре. В случае, когда
происходит взаимодействие равных, либо не сильно отличающихся по
массе частиц используют модифицированную формулу (Дарвин, 1914 г.):
2
dσ z1 z2 e 2
4
=
dΩ 4T sin 4 θ
{ [1 − ((M / M ) sin θ ) ]
2 1/ 2
1
[1 − ((M
2
2
1 / M 2 ) sin θ )
+ cos θ
]
1/ 2
}
2
,
(6.41)
получившую название - формула Дарвина.
Анализируя формулы Резерфорда и Дарвина несложно убедиться, что
сечение упругого взаимодействия будет велико при рассеянии на малые
углы и небольших значениях кинетической энергии заряженной частицы.
Для тяжелых заряженных частиц это будет приводить к тому, что упругое
рассеяние появится только в конце пробега частицы в среде, траектория
движения частицы на данном отрезке не претерпит существенных
изменений, а пробег будет соответствовать указанному на рис. 6.4.
На основе упругого рассеяния реализованы методы анализа состава и
структуры твердых тел: резерфордовское обратное рассеяние (РОР), ядра
отдачи
(ЯО).
Энергия
рассеянных
частиц
служит
качественным
показателем состава твердого тела и распределения атомов по глубине, а
19
количество
зарегистрированных
частиц
–
дает
информацию
о
концентрации атомов того или иного сорта.
6.2.6. Многократное рассеяние заряженных частиц
При движении заряженной частицы в среде с толщиной, равной, либо
больше пробега данной частицы в среде может возникать ситуация, когда
последняя испытывает не одно упругое рассеяние, а большое количество
последовательных актов рассеяния на малые углы. Такой процесс
называется многократным рассеянием и вносит вклад в общие потери
энергии заряженной частицы и изменение геометрических факторов пучка
частиц (поперечное сечение, разброс длины пути и др.). Основной
характеристикой, описывающей многократное рассеяние, является угол
многократного рассеяния Θ.
Предположим, что частица с зарядом z и кинетической энергией Т,
пройдя путь х, в результате многократного рассеяния на ядрах Z
отклонится на результирующий угол Θ 1 , проекция которого на плоскость
α1
z
x
Рис. 6.6
чертежа обозначим за α 1 (рис. 6.6).
Для К -ой частицы соответственно Θ К и α К . В силу равновероятного
отклонения частиц во все направления среднее значение проекций углов
отклонения:
αi
= 0.
i =1 K
K
α =∑
20
(6.42)
Поэтому, реальное представление о процессе многократного рассеяния
__
дает среднее значение квадратов проекций углов α 2 :
__
2
K
α i2
i =1
K
α =∑
,
(6.43)
являющейся положительной величиной.
Средний квадрат самих пространственных углов многократного рассеяния
задается как:
__
2
__
2
Θ = 2α .
(6.44)
Тогда средний угол многократного рассеяния равен:
__
2
Θ= Θ .
(6.45)
С другой стороны:
__
2
__
2
N
__
2
i
Θ = 2 α = ∑θ ,
i =1
(6.46)
__
2
где усреднение θ i происходит по К траекториям. Поскольку акты
__
2
i
рассеяния происходят на одинаковых ядрах, то θ одинаково для любого i__
__
2
2
ого ядра ( θ i = θ ) и, исходя из (6.46):
__
2
__
2
Θ = Nθ ,
(6.47)
__
где N – число ядер, встретившихся частице на пути х, а θ 2 получается
усреднением по всем параметрам удара ρ. С учетом, что для малых углов
tg (θ / 2) ≈ θ / 2 , а tg (θ / 2) = rmin / 2 ρ , где rmin = ( z Z e 2 ) / T для θ 2 в зависимости от
параметра удара имеем:
4 z 2 Z 2 e4 1
.
θ (ρ ) =
m 2v 4 ρ 2
2
21
(6.48)
Число столкновений заряженной частицы на пути х, приводящих к
отклонению на угол θ можно выразить аналогично (6.4) и рис. 6.2:
dN ( ρ ) = 2π n x ρ dρ .
(6.49)
__
Тогда усреднение θ 2 сводится к вычислению интеграла вида:
ρmax
__
2
θ =
∫ρ θ
min
2
ρmax
( ρ ) dN ( ρ )
ρmax
∫
=
8π n x z 2 Z 2 e 4 dρ
∫
m 2v 4
ρ
ρmin
N
dN ( ρ )
.
(6.50)
ρmin
Следовательно:
ρ max
8π n x z 2 Z 2 e 4 dρ 8π n x z 2 Z 2 e 4 ρ max
Θ = Nθ = ∫
∝
ln
.
2 4
2 4
m
v
ρ
m
v
ρ
min
ρ min
__
2
__
2
(6.51)
Окончательная оценка ρ min и ρ max дает выражение для среднего значения
квадрата угла многократного рассеяния:
2
Z 4 / 3 zx
Z ( Z + 1) z x
4
,
ln 1,13 ⋅ 10
Θ = 0,157
2
2 4
A
mv
A β
__
2
(6.52)
а для угла многократного рассеяния имеем пропорциональность вида:
__
2
Θ= Θ ∝
z x
.
mv 2
(6.53)
6.2.7. Особенности взаимодействия электронов с веществом
Электроны являются более легкими частицами по массе (в 1836 раз),
чем самые легкие ионы (протоны). Этим определяются некоторые отличия
в ионизационных потерях энергии, упругом многократном рассеянии при
движении электронов и ионов в среде.
Формула для ионизационных потерь электронов имеет несколько
отличный вид от выражения (6.11):
22
−
me v 2Te
dT 2π e 4 nат
1
Z
=
− ln 2 (2 1 − β 2 − 1 + β 2 ) + 1 − β 2 + (1 − 1 − β 2 ) 2 − δ , (6.54)
ln
2
2
2
dx
8
me v
2 I (1 − β )
где
Te -
релятивистская
кинетическая
энергия.
Основное
отличие
ионизационных потерь электронов от ионов связано с тем, что в акте
взаимодействии двух электронов необходимо учитывать отклонение обеих
частиц, а также квантово – механический эффект обмена, обусловленный
тождественностью частиц. Эффект плотности аналогично взаимодействию
тяжелых заряженных частиц возникает при больших энергиях электронов.
При движении электронов в среде, на траекторию частиц существенно
влияет упругое рассеяние. На качественном уровне в этом движении
можно выделить три этапа, которые определяются толщиной среды:
1. Первоначально быстрые электроны проходят некоторый отрезок
пути
прямолинейно,
теряя
энергию
и
испытывая
незначительное
отклонение за счет малого числа актов малоуглового упругого рассеяния.
2. С увеличением толщины среды энергия электронов уменьшается, а
вероятность упругого рассеяния возрастает. На этом этапе реализуется
процесс многократного упругого рассеяния. При этом угол многократного
рассеяния согласно (6.53) Θ ∝ x .
3. С последующим уменьшением
Ne
энергии электронов и приближении
толщины среды к величине пробега
электронов в данной среде, число актов
упругого
настолько
рассеяния
большим,
2
1
становится
что
угловое
распределение движения электронов в
Rэфф
x
Рис. 6.8
среде становится диффузным. То есть в
конце пробега в веществе направление движения электронов никак не
связано с первоначальным направлением влета частиц в вещество.
23
Таким образом, в отличие от ионов,
dN
число электронов, прошедших среду с dT
заданной
толщиной,
является
1
постепенно уменьшающейся функцией
толщины этой среды.
2
Рассмотрим прохождение в среде
электронов
сплошного
Te
спектра
Рис. 6.7
естественного радионуклида и спектра
моноэнергетичных электронов (рис 6.7, 1 – сплошной спектр, 2 – спектр
моноэнергетичных электронов). Зависимость изменения плотности потока
от толщины среды для обоих спектров показана на рис. 6.8 (1 – для
сплошного спектра, 2 – для спектра моноэнергетичных электронов).
Видно, что ход кривых существенно отличается от аналогичной для
тяжелых ионов (рис. 6.4). Только зависимость для моноэнергетичных
электронов лишь отчасти на первоначальном этапе напоминает характер
кривой изменения плотности потока ионов от толщины среды (рис.6.4).
При этом обе зависимости на рис. 6.8. не могут быть полностью описаны
теоретически. Лишь зависимость 1 на некоторых участках может
подчиняться экспоненциальному закону:
N = N 0 ⋅ e −σ ⋅ n ⋅ x ,
(6.55)
где N 0 - начальный поток электронов, σ - сечение взаимодействия
электронов с веществом и x -толщина мишени. Произведение
σ ⋅ n = µ,
(6.56)
называется коэффициентом ослабления и является характеристикой
данного вещества. Единица измерения - [µ ]= см-1. Аналогично массовым
тормозным потерям вводят и массовый коэффициент ослабления
µm =
24
µ
,
ρ
(6.57)
где ρ - плотность данного вещества. Единица измерения - [µ m ] = см 2 / г .
Характерная толщина мишени, в которой будет выполняться
экспоненциальный закон ослабления, рассчитывается с учетом значения
характеристик данного вещества, т.е. величины µ. Взяв обратное значение
1/µ, получим значение толщины мишени, где ослабление пучка электронов
будет идти согласно (6.55). Необходимо отметить, что для большинства
веществ и естественных радионуклидных источников электронов эти
значения малы и не превышают 1-2 мм, тогда как пробеги этих электронов
существенно больше, поэтому кривая ослабления для естественных
радионуклидов не может описываться выражением (6.55) на всех участках.
Зависимость 2 на рис. 6.8 слабо поддается теоретическому описанию,
поэтому
для
изучения
ослабления
таких
электронов
используют
эмпирические методы определения пробегов. Измерение зависимости на
рис. 6.8 методом поглощения дает значение пробега электронов данной
энергии в веществе. Спроецировав прямолинейный участок кривой
ослабления пучка электронов на ось абсцисс (толщины среды), можно
получить эффективный пробег - R эфф . Большинство эффективных пробегов
для электронов различных энергий получено таким эмпирическим путем.
При этом если наблюдается определенная закономерность зависимости
величины пробега электронов от энергии, то для определенных
энергетических
диапазонов
получают
эмпирические
формулы
и
используют их на практике для вычисления пробегов. Например, формулы
R = 0,407 ⋅ Te1,38 г / см 2 ,
R = 0,542 ⋅ Te − 0,133 г / см 2 .
(6.56)
дают возможность получить величину пробега электронов в алюминии для
диапазонов энергий соответственно 0,15 ≤ Te ≤ 0,8 МэВ и Te ≥ 0,8 МэВ.
25
6.2.8. Радиационное торможение заряженных частиц в среде
Следующим эффектом, протекающим под действием заряженных
частиц в веществе является тормозное излучение (ТИ). ТИ – это
электромагнитное излучение, испускаемое заряженной частицей при
торможении в электрическом поле ядра или атомных электронов.
Согласно классической электродинамике, интенсивность тормозного
излучения пропорциональна квадрату ускорения, испытываемого частицей
2
𝑓𝑓
𝐽𝐽~𝑎𝑎2 . Поскольку ускорение 𝑎𝑎 = �𝑚𝑚, то в конечном итоге 𝐽𝐽~ 𝑍𝑍 � 2 , где
𝑚𝑚
Z – порядковый номер ядра, f – сила кулоновского взаимодействия ядра и
заряженной частицы, m – масса заряженной частицы. Таким образом,
тормозное излучение будет наиболее вероятным процессом для легких
частиц – электронов.
Спектр тормозного излучения является непрерывным и обрывается
при энергии квантов, равной начальной энергии заряженной частицы (рис.
6.9). Угловое распределение тормозного
излучения
𝑑𝑑𝑑𝑑
𝑑𝑑𝑑𝑑
существенно
зависит
от
скорости и энергии заряженной частицы:
если кинетическая энергия существенно
меньше
энергии
частицы
𝑇𝑇 ≪ 𝑚𝑚𝑐𝑐 2 ,
покоя
то
заряженной
интенсивность
тормозного излучения максимальна в
Рис. 6.9
𝐸𝐸
направлении
направлению
перпендикулярно
движения
заряженной
частицы (рис. 6.10, а), в противоположном случае, когда энергия 𝑇𝑇 ≫ 𝑚𝑚𝑐𝑐 2
интенсивность ТИ максимальна вдоль направления движения заряженной
частицы (рис. 6.10, б). ТИ испускается в конусе со средним углом
2
𝑚𝑚 𝑐𝑐
𝜃𝜃̅ = 𝑇𝑇 .
26
(6.57)
б)
a)
𝑥𝑥
𝑥𝑥
Рис. 6.10
Теория тормозного излучения была построена в 1934 г. Бете и
Гайтлером, в которой потери энергии заряженной частицы �−
ТИ
описываются
формулой,
учитывающей
торможение
𝑑𝑑𝑑𝑑
�
на
𝑇𝑇+𝑝𝑝𝑝𝑝
− +
𝑑𝑑𝑑𝑑 изл.
только
в
электрическом поле ядра:
�−
𝑑𝑑𝑑𝑑
�
𝑑𝑑𝑑𝑑 изл.
12𝑇𝑇 2 +4𝑚𝑚 2 𝑐𝑐 4
= 𝛼𝛼𝑛𝑛𝑍𝑍 2 𝑟𝑟𝑒𝑒2 𝑇𝑇 �
𝜉𝜉 ln
(1+𝑥𝑥)
где 𝐹𝐹 (𝜉𝜉) = ∫0
𝑥𝑥
3𝐸𝐸𝐸𝐸𝐸𝐸
+
2𝑚𝑚 2 𝑐𝑐 4
𝑇𝑇𝑇𝑇𝑇𝑇
𝑙𝑙𝑙𝑙
𝑇𝑇+𝑝𝑝𝑝𝑝
𝑚𝑚 𝑐𝑐 2
−
(8𝑇𝑇+6𝑝𝑝𝑝𝑝 )𝑚𝑚 2 𝑐𝑐 4
3𝑇𝑇𝑝𝑝 2 𝑐𝑐 2
2𝑝𝑝𝑝𝑝 (𝑇𝑇+𝑝𝑝𝑝𝑝 )
∙ 𝐹𝐹(𝜉𝜉) ∙ �
𝑚𝑚 2 𝑐𝑐 4
��,
𝑙𝑙𝑙𝑙2
𝑚𝑚 𝑐𝑐 2
4
3
(6.58)
𝑑𝑑𝑑𝑑 – трансцендентная функция Спенса, n –
концентрация атомов среды, 𝑟𝑟𝑒𝑒 – классический радиус электрона, 𝛼𝛼 =
𝑒𝑒 2� = 1�
137 − постоянная тонкой структуры.
ℏ𝑐𝑐
В
нерелятивистском
случае,
упрощается т.к. 𝜉𝜉 ≪ 1 и 𝐹𝐹 (𝜉𝜉) ≈ 𝜉𝜉:
𝑑𝑑𝑑𝑑
�− 𝑑𝑑𝑑𝑑 �
В
изл.
ультрарелятивистском
когда
=
16
3
𝛼𝛼𝑛𝑛𝑍𝑍 2 𝑟𝑟𝑒𝑒2 𝑇𝑇.
случае,
1
𝑇𝑇 ≪ 𝑚𝑚𝑐𝑐 2
когда
формула
𝑇𝑇 ≫ 𝑚𝑚𝑐𝑐 2 ,
(6.58)
(6.59)
𝜉𝜉 ≫ 1
и
𝐹𝐹 (𝜉𝜉) ≈ 2 𝑙𝑙𝑙𝑙2 𝜉𝜉, оба члена в (6.17), содержащие 𝑙𝑙𝑙𝑙2 могут быть опущены и
(6.17) приобретает вид:
27
𝑑𝑑𝑑𝑑
�− 𝑑𝑑𝑑𝑑 �
изл.
2𝑇𝑇
1
= 4𝛼𝛼𝑛𝑛𝑍𝑍 2 𝑟𝑟𝑒𝑒2 �𝑙𝑙𝑙𝑙 𝑚𝑚 𝑐𝑐 2 − 3�.
(6.60)
Дальнейшее уточнение теории тормозного излучения достигается
учетом экранирования ядра атомными электронами. Поправки на
экранирование существенны при 𝑇𝑇 ≫ 𝑚𝑚𝑐𝑐 2 и приводят к снижению
интенсивности ТИ:
𝑑𝑑𝑑𝑑
�− 𝑑𝑑𝑑𝑑 �
изл.
= 4𝛼𝛼𝑛𝑛𝑍𝑍 2 𝑟𝑟𝑒𝑒2 𝑇𝑇 �𝑙𝑙𝑙𝑙
1
1 �.
𝛼𝛼𝑍𝑍 �3
(6.61)
При столкновении заряженной частицы с атомом необходимо иметь
ввиду, что тормозное излучение происходит и на атомных электронах.
Наличие атомных электронов в (6.58-6.61) можно приблизительно учесть
заменой 𝑍𝑍 2 на 𝑍𝑍(𝑍𝑍 + 1) = 𝑍𝑍 2 + 𝑍𝑍. Анализ (6.59-6.61) показывает, что в
общем случае потери энергии заряженной частицы пропорциональны 𝑍𝑍 2 и
n – величинам, характеризующим вещество и энергии самой частицы
𝑑𝑑𝑑𝑑
�− 𝑑𝑑𝑑𝑑 �
изл.
~ 𝑛𝑛𝑍𝑍 2 T,
(6.62)
т.е. испускание тормозного излучения наиболее вероятно при движении
заряженной частицы с большой энергией в тяжелой среде.
Если уравнение (6.61) переписать в виде
𝑑𝑑𝑑𝑑
где 𝑥𝑥рад = �4𝛼𝛼𝑛𝑛𝑍𝑍 2 𝑟𝑟𝑒𝑒2 �𝑙𝑙𝑙𝑙
�𝑑𝑑𝑑𝑑 �
1
изл.
−1
1 ��
𝛼𝛼𝑍𝑍 �3
= − 𝑥𝑥
𝑇𝑇
рад
,
(6.63)
есть радиационная длина, то решение
данного дифференциального уравнения даст выражение, связывающее
начальную и конечную энергию заряженной частицы при прохождении
слоя вещества
𝑇𝑇 = 𝑇𝑇0 𝑒𝑒
28
−
𝑥𝑥
𝑥𝑥 рад
.
(6.64)
Таким образом, уравнение (6.64) определяет характерную толщину
вещества, при прохождении которой энергия заряженной частицы убывает
экспоненциально в связи с тормозным излучением.
Сравнение уравнений (6.12) и (6.62) показывает, что и ионизационные
и радиационные потери энергии заряженной частицы зависят от
концентрации ядер и порядкового номера вещества, в котором движется
частица. В то же время ионизационные потери обратно пропорциональны,
а радиационные – прямо пропорциональны энергии заряженной частицы.
Следовательно, при движении быстрой заряженной частицы в веществе
сначала будут преобладать радиационные потери, а с дальнейшим
уменьшением энергии заряженной частицы будут расти ионизационные
потери.
Тогда
при
определенной
энергии
заряженной
частицы
ионизационные и радиационные потери в данном веществе сравняются.
Такая энергия называется критической 𝑇𝑇кр , а ее значение можно получить
исходя из сравнения (6.12) и (6.62):
𝑑𝑑𝑑𝑑
�
𝑑𝑑𝑑𝑑 рад
𝑑𝑑𝑑𝑑
�− �
𝑑𝑑𝑑𝑑 ион
�−
~
𝑛𝑛 𝑍𝑍 2 𝑇𝑇
𝑛𝑛𝑛𝑛
= 𝑍𝑍𝑍𝑍,
(6.65)
или с учетом всех констант можно получить следующее выражение:
𝑑𝑑𝑑𝑑
�
𝑑𝑑𝑑𝑑 рад
𝑑𝑑𝑑𝑑
�− �
𝑑𝑑𝑑𝑑 ион
�−
𝑍𝑍𝑍𝑍 [МэВ]
= 1600∙𝑚𝑚 𝑐𝑐 2 [
МэВ]
,
(6.66)
где 𝑚𝑚𝑐𝑐 2 – энергия покоя налетающей частицы. Таким образом, энергия,
при которой отношение энергетических потерь заряженной частицы
согласно (6.66) будет равно единице, является критической энергией.
Учитывая, что для электронов энергия покоя составляет 0,511 МэВ,
(6.66) трансформируется в
29
𝑑𝑑𝑑𝑑
�
𝑑𝑑𝑑𝑑 рад
𝑑𝑑𝑑𝑑
�− �
𝑑𝑑𝑑𝑑 ион
�−
𝑍𝑍𝑍𝑍
≅ 800 .
(6.67)
Например, в свинце с Z=82 значение критической энергии для электронов
составляет 𝑇𝑇кр ≅ 10 МэВ, для воды 𝑇𝑇кр ≅ 100 МэВ.
6.2.9. Излучение Вавилова-Черенкова
Кроме основных эффектов ионизации, тормозного излучения и
упругого рассеяния на ядрах, протекающих под действием заряженных
частиц, рассмотренных выше, при определенных условиях возможно
протекание ряда дополнительных эффектов. Одним из них является
излучение Вавилова-Черенкова (ИВЧ).
ИВЧ – это электромагнитное излучение, которое возникает при
движении заряженной частицы в среде со скоростью, превышающей
скорость света в данной среде. То есть скорость частицы
𝑐𝑐
𝑣𝑣 ≥ 𝑐𝑐 ′ = 𝑛𝑛 ,
(6.68)
где 𝑐𝑐 ′ - скорость света в среде, 𝑛𝑛 – показатель преломления данной среды.
Одним из основных свойств ИВЧ, установленных экспериментально,
является отсутствие зависимости интенсивности излучения от заряда
атомов среды Z, поэтому излучение Вавилова-Черенкова не может быть
радиационного происхождения.
Излучение Вавилова-Черенкова с фиксированной частотой имеет
строго определенную угловую направленность. Оно испускается под
фиксированным углом 𝜃𝜃 вдоль образующих конуса, ось которого
совпадает с направлением движения частицы, а угол раствора равен 2 𝜃𝜃,
т.е.
симметрично
по
азимутальному
углу
(рис.
6.11).
экспериментально было обнаружено,
что источником ИВЧ является среда, в
30
𝑣𝑣⃗
𝜃𝜃
Рис. 6.11
Также
которой движется заряженная частица, а преобразование энергии частицы
в ИВЧ происходит посредством среды без возбуждения атомов данной
среды. Данный факт означает, что диссипации энергии, теряемой
заряженной частицей в среде не происходит. Таким образом, изменение
энергии и импульса частицы при генерации ИВЧ равно по модулю энергии
и импульсу фотонов излучения Вавилова-Черенкова. Следовательно,
записав законы сохранения и импульса в виде
𝑑𝑑𝐸𝐸част = 𝑑𝑑𝐸𝐸изл ,
(6.69)
1
𝑑𝑑𝑃𝑃част = cos 𝜃𝜃 𝑑𝑑𝑃𝑃изл ,
и поделив уравнения системы друг на друга получим соотношение:
1
Производная
𝑑𝑑𝑑𝑑
𝑑𝑑𝑑𝑑
𝑑𝑑𝐸𝐸изл
cos 𝜃𝜃 𝑑𝑑𝑃𝑃изл
𝑑𝑑𝐸𝐸
= 𝑑𝑑𝑃𝑃част.
част
(6.70)
с учетом, что полная энергия 𝐸𝐸 = �𝑚𝑚2 𝑐𝑐 4 + 𝑝𝑝2 𝑐𝑐 2 , будет
равна скорости частицы:
𝑑𝑑𝑑𝑑
𝑑𝑑𝑑𝑑
=
𝑝𝑝𝑐𝑐 2
𝐸𝐸
= 𝛽𝛽𝛽𝛽 = 𝑣𝑣.
(6.71)
Тогда, исходя из уравнений (6.70) и (6.71) можно заключить, что
излучение со свойствами ИВЧ должно наблюдаться, если проекция
скорости частицы на направление движения фотона равна скорости
фотонов в данной среде:
откуда
𝑣𝑣 cos 𝜃𝜃 = 𝑐𝑐′,
cos 𝜃𝜃 =
𝑐𝑐 ′
𝑣𝑣
𝑐𝑐
(6.72)
1
= 𝑛𝑛𝑛𝑛 = 𝛽𝛽𝛽𝛽 .
(6.73)
Условие (6.73) определяет угол, под которым появляется ИВЧ. Квантовомеханический расчет дает более точное выражение
𝜆𝜆 𝑝𝑝
1
1
cos 𝜃𝜃 = 𝛽𝛽𝛽𝛽 + 2𝜆𝜆 �1 − 𝑛𝑛 2 �,
31
(6.74)
где 𝜆𝜆𝑝𝑝 =
ℎ
𝑝𝑝
де-бройлевская длина волны заряженной частицы с массой m и
скоростью v, 𝜆𝜆 - длина волны ИВЧ. Обычно
𝜆𝜆 𝑝𝑝
𝜆𝜆
≪ 1.
Из уравнения (6.73) следует, что ИВЧ будет наблюдаться при
скорости заряженной частицы, превышающей фазовую скорость света в
данной среде, т.е. в диапазоне
При v =
c
n
𝑐𝑐
𝑛𝑛
≤ 𝑣𝑣 ≤ 𝑐𝑐
1
или
𝑛𝑛
≤ 𝛽𝛽 ≤ 1.
(6.75)
излучение Вавилова-Черенкова наблюдается под углом
(1�n)
θ = 0, а при v = c под максимальным углом θmax = arccos
Физический механизм ИВЧ заключается в том, что при 𝑣𝑣 ≥ 𝑐𝑐 ′ среда
под действием электрического поля частицы поляризуется лишь в
«кильватере» траектории (рис.6.12), т.е.
наблюдается
эффект
поляризации
среды.
запаздывания
В
результате
𝑥𝑥
образовавшиеся диполи будут иметь
преимущественную
ориентацию
в
направлении движения частицы. Такое
состояние
среды
является
возбужденным, а когерентное излучение
такой группы диполей приводит к
Рис. 6.12
возникновению ИВЧ. Подчеркнем, что излучение Вавилова-Черенкова не
имеет ничего общего с фактически всегда имеющим место тормозным
излучением. Последнее испускается самой движущейся частицей при ее
сталкивании с атомами, ИВЧ же обусловлено излучением, испускаемым
средой под влиянием движущейся заряженной частицы. Различие между
этими излучениями проявляется особенно ясно при переходе к пределу
32
сколь угодно большой массе частицы: тормозное излучение при этом
исчезает вовсе, а ИВЧ вообще не изменяется.
Показатель преломления среды есть функция частоты излучения
𝑛𝑛 = 𝑛𝑛(𝜔𝜔 = 2𝜋𝜋𝜋𝜋). Поэтому излучению данной частоты 𝜔𝜔 соответствует
вполне определенное значение угла 𝜃𝜃, определяемое формулой (6.73).
Диапазон частот, в котором происходит ИВЧ, определяется условием
В
частности
при
𝛽𝛽𝛽𝛽(𝜔𝜔) ≥ 1.
𝛽𝛽𝛽𝛽(𝜔𝜔) = 1
(6.76)
определяется
значение
максимально
возможной частоты 𝜔𝜔𝑚𝑚𝑚𝑚𝑚𝑚 ИВЧ. Обычно частота ИВЧ заключена в
пределах 0 ≤ 𝜔𝜔 ≤ 𝜔𝜔𝑚𝑚𝑚𝑚𝑚𝑚 .
Теория ИВЧ построена И.Е.Таммом и И.И.Франком в 1937 году.
Согласно этой теории число фотонов ИВЧ с частотой в интервале [𝜔𝜔, 𝜔𝜔 +
𝑑𝑑𝜔𝜔], появляющихся с участка dx пути заряженной частицы в среде
𝑑𝑑 2 𝑁𝑁
𝑑𝑑𝑑𝑑
=
𝑧𝑧 2 𝑒𝑒 2
ℏ𝑐𝑐 2
�1 −
1
𝑛𝑛 2 𝛽𝛽 2
� ∙ 𝑑𝑑𝑑𝑑.
(6.77)
Из (6.77) можно сделать следующие заключения:
1. Спектр ИВЧ является одинаковым для частиц с 𝑧𝑧 = 𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐, при
увеличении 𝑧𝑧 число фотонов растет пропорционально 𝑧𝑧 2 .
2. Число фотонов растет с увеличением скорости частицы от нуля при
𝛽𝛽 =
1
𝑛𝑛
до
𝑧𝑧 2 𝑒𝑒 2
ℏ𝑐𝑐 2
1
�1 − 𝑛𝑛 2 𝛽𝛽 2 � при 𝛽𝛽 = 1.
3. Число фотонов не зависит от частоты излучения 𝜔𝜔.
4. Интенсивность ИВЧ будет максимальна в той области спектра, в
которой показатель преломления достигает наибольшего значения. Полная
интенсивность фотонов ИВЧ задается интегралом от (6.77) по всем
частотам.
Основное применение ИВЧ – это Черенковские счетчики заряженных
частиц, предназначенные для определения скорости и энергии заряженных
частиц. Пусть заряженная частица движется по направлению вдоль оси
33
𝑂𝑂𝑂𝑂′ (рис. 6.13) и попадает в среду, при движении в которой возникает ИВЧ
𝜃𝜃
𝜑𝜑
ФЭУ
Рис. 6.13
1
𝜋𝜋
под углом 𝜃𝜃 < 𝜃𝜃𝑚𝑚𝑚𝑚𝑚𝑚 = 𝑎𝑎𝑎𝑎𝑎𝑎𝑎𝑎𝑎𝑎𝑎𝑎 . Угол 𝜑𝜑 = − 𝜃𝜃 при этом будет принимать
1
𝑛𝑛
2
значения 𝜑𝜑 > 𝜑𝜑0 = 𝑎𝑎𝑎𝑎𝑎𝑎𝑎𝑎𝑎𝑎𝑎𝑎 , а это есть условие полного отражения
𝑛𝑛
излучения от границы раздела сред счетчика и внешней среды. После
нескольких актов полного отражения ИВЧ попадает на собирающую линзу
и далее в фотоэлектронный умножитель.
Таким образом, возможен счет частиц определенной энергии на
основе черенковского излучения. Основной материал, из которого
изготавливаются черенковские счетчики – прозрачные пластмассы.
6.2.10. Переходное излучение
Еще одним видом взаимодействия заряженных частиц с веществом,
реализующимся в определенных условиях, является переходное излучение
(ПИ). ПИ – это излучение, возникающее при равномерном прямолинейном
движении заряженной частицы (𝑧𝑧𝑒𝑒) в неоднородной или переменной во
времени среде. Данная ситуация может быть реализована при переходе
заряженной частицы из одной среды в другую, либо при резком
изменении, например, давления среды, в которой движется частица.
Переходное излучение может возникать как при
34
𝑣𝑣∙𝑛𝑛
𝑐𝑐
> 1 так и при
𝑣𝑣∙𝑛𝑛
𝑐𝑐
< 1,
где 𝑣𝑣 – скорость движения частицы, 𝑛𝑛 - показатель преломления среды, с -
скорость света, т.е. ПИ излучение может возникать как совместно с ИВЧ,
так и без него.
Переходное
излучение
было
𝑒𝑒 −
предсказано в 1944 г. и качественно
объяснено
на
примере
задачи
о
1
𝛾𝛾
пересечении заряженной частицей границы
двух сред (рис. 6.14) В.Л.Гинзбургом и
И.М.Франком.
Если
рассмотреть
движение, например электрона, к границе
раздела
вакуум
-
идеальное
зеркало
𝑒𝑒 +
3
Рис. 6.14
𝑒𝑒 −
2
(металл), то процесс рождения ПИ, при рассмотрении этого явления из
вакуума, можно представить как аннигиляцию электрона с собственным
изображением (противоположного знака) на границе раздела двух сред. В
этом случае ПИ можно рассматривать как эквивалент ТИ, т.к. обе частицы
формально останавливаются на границе раздела, однако это не означает,
что переходное излучение является частным случаем тормозного
излучения. В реалии же электрон продолжает свое движение в среде с
постоянной скоростью, а на границе раздела сред резко изменяется
фазовая скорость электромагнитной волны, описывающей заряженную
частицу.
В общем случае, при движении заряженной частицы через границу
произвольных сред, механизм определения спектра ПИ учитывает три
составляющих: 1) тормозное излучение частицы 1, движущейся и
формально остановившейся на границе раздела двух сред, 2) тормозное
излучение частицы 2, формально начавшей движение от границы раздела
двух сред вглубь, 3) тормозное излучение частицы 3 (изображения
частицы 1), двигавшейся навстречу первой и формально остановившейся
на границе раздела вместе с частицей 1.
35
Спектральная
плотность
переходного
излучения
электрона,
приходящаяся на телесный угол, при движении из вакуума в идеальный
проводник задается выражением:
𝑑𝑑𝑑𝑑
𝑑𝑑Ω
=
𝑒𝑒 2 ∙𝑣𝑣𝑧𝑧2
𝜋𝜋 2 ∙𝑐𝑐 3
𝑠𝑠𝑠𝑠𝑠𝑠2 𝜑𝜑.
(6.78)
Из (6.78) видно, что максимум плотности излучения приходится на
угол 90°. Однако для реальных металлов и полупроводников угол, под
которым испускается максимум плотности излучения, составляет 𝜑𝜑 =
60 − 70°.
При движении заряженной частицы из вакуума в бесконечную по
толщине среду сопровождается переходным излучением только в
обратном направлении. Угол 𝜑𝜑 берется между нормалью к поверхности
среды и направлением ПИ. В случае движения заряженной частицы из
вакуума в тонкую среду ПИ изучение может наблюдаться как в обратном
направлении при переходе первой границы, так и в направлении вперед
при обратном переходе из среды в вакуум. Спектр ПИ излучения в
обратном направлении содержит свечение с длинами волн видимого
диапазона (характерным примером является свечение анода рентгеновской
трубки). Спектр ПИ вперед содержит более высокие частоты вплоть до
значений 𝜈𝜈𝑚𝑚𝑚𝑚𝑚𝑚 = 9 ∙ 103 √𝑁𝑁
𝐸𝐸
𝑚𝑚 𝑐𝑐 2
, где N – полная концентрация электронов в
среде. Например, для электронов с энергией 500 МэВ при переходе в
стекло (N=1024 см-3) частота излучения 𝜈𝜈 = 1019 Гц, а энергия излучения
𝐸𝐸 = ℎ𝜈𝜈 = 40 кэВ. Основное применение ПИ нашло при регистрации
заряженных частиц с высокими энергиями, когда вероятность данного
типа взаимодействия становится больше, чем других (тормозного
излучения, ионизационного торможения, рассеяния и др.).
36
6.2.11. Синхротронное излучение
Синхротронное излучение (СИ) было открыто в 1947 г. молодым
ученым Ф. Хабером во время наладки ускорителя заряженных частиц –
синхротрона, рассчитанного на энергию электронов в 100 МэВ. Во время
инженерных
работ
было
снято
внешнее
непрозрачное
покрытие
ускорительной камеры и образовавшееся окно дало возможность
«электронному свету» выйти за ее пределы.
Таким образом, СИ возникает при движении заряженной частицы с
постоянной скоростью по криволинейной траектории. Такое движение
является
движением
с
ускорением
и,
следовательно,
должно
сопровождаться излучением заряженной частицы. СИ получают на
ускорителях кольцевого типа – синхротронах (поэтому излучение и носит
название синхротронного), предназначенных для ускорения электронов до
релятивистских энергий.
Свойства СИ существенно зависят от энергии и массы заряженной
частицы. Пространственное распределение мощности синхротронного
излучения нерелятивистского электрона описывается тороидом (рис. 6.15,
(а)),
причем
относительно
максимум
излучения
направления
приходится
движения
частицы.
на
При
угол
𝜓𝜓´= π/2
достижении
электроном релятивистской энергии 𝑇𝑇𝑒𝑒 , когда 𝛽𝛽 → 1 и 𝛾𝛾 =
𝑇𝑇𝑒𝑒
𝑚𝑚 𝑒𝑒 𝑐𝑐 2
≫ 1,
тороид вследствие эффекта Доплера сильно деформируется и вытягивается
в конус вдоль вектора скорости электрона (рис. 6.15, (б)). СИ в этом случае
обладает резко выраженным прожекторным эффектом, испускается по
касательной к траектории движения частицы и имеет пространственное
распределение, описываемое половинным углом раствора:
𝜓𝜓 =
𝑚𝑚 𝑒𝑒 𝑐𝑐 2
𝑇𝑇𝑒𝑒
1
= .
37
𝛾𝛾
(6.79)
Рис. 6.15. Угловое распределение мощности синхротронного излучения:
(а) – нерелятивистская частица, (б) – релятивистская частица
Чем больше энергия заряженной частицы, тем меньше угловая
расходимость излучения, т.е. СИ сильно коллимировано.
Другим свойством СИ, также связанным с эффектом Доплера,
является его спектральное распределение. Для наблюдателя, находящегося
в
лабораторной
системе
координат,
полная
масса
частицы
на
релятивистских и ультрарелятивистских скоростях начинает зависеть от
скорости, как m = m 0 γ. Происходит релятивистское лоренцовское сжатие
длины волны излучения в γ раз и доплеровский сдвиг частоты излучаемых
электромагнитных волн в сторону более высоких частот 𝜔𝜔 >> 𝜔𝜔 c , где 𝜔𝜔 c –
R
R
частота вращения электрона в ускорителе. Таким образом, основная доля
излучаемой энергии оказывается сдвинутой в более высокие частоты, а
максимум СИ приходится на частоту
𝜔𝜔0 = 𝜔𝜔с ∙ 𝛾𝛾 3 .
38
(6.80)
Учитывая, что частота 𝜔𝜔с зависит от параметров ускорения, значение
𝜔𝜔0 можно выразить через напряженность магнитного поля Н (Гс) и
энергию электронов 𝑇𝑇𝑒𝑒 (эВ)
𝜔𝜔0 = 4,6 ∙ 10−6 𝐻𝐻𝑇𝑇𝑒𝑒2 .
(6.81)
Так для напряженности поля Н= 104 Гс и энергии электронов 100 МэВ
спектр СИ испускается в конус с 𝜃𝜃 = 17′ и имеет максимум при
𝜔𝜔0 ≈ 1015 Гц.
Таким образом, спектр СИ включает в себя высшие гармоники
основной
частоты,
𝛾𝛾 3 .
Для
1015-1019
Гц.
пропорциональные
релятивистских
и
ультрарелятивистских электронов (сотни МэВ – десятки ГэВ) диапазон
частот на которые приходится максимум СИ, лежит в области значений
𝑑𝑑𝑑𝑑
𝑑𝑑𝑑𝑑
интервалы
частотами
В
этой
между
области
кратными
(гармониками)
малы
настолько, что их распределение в
спектре практически сливается и
спектр синхротронного излучения
Рис. 6.16
𝜔𝜔0
𝜔𝜔
можно считать непрерывным (рис.
6.16).
Важно отметить, что, если электрон испускает синхротронное
излучение в области рентгеновских частот на высших гармониках, то
одновременно излучаются и более низкие частоты вплоть до частоты
обращения электрона по орбите, которая соответствует диапазону УКВ
или СВЧ волн. Это значит, что спектр синхротронного излучения
простирается от радиоволн до рентгеновских лучей, включая ИК-, УФизлучение и видимый свет, и поэтому синхротронное излучение можно
наблюдать визуально как яркий пучок света, что имеет место на самом
деле, если сделать прозрачное окно в камере синхротрона. Пример
39
спектрального распределения СИ для ряда синхротронов показан на рис.
6.17.
Рис. 6.16. Примеры спектров СИ накопителей с энергиями электронов: ALS
(E=1,9 ГэВ); APS (E = 7 ГэВ); NSLS (E = 2,8 ГэВ); SSRL (SPEAR-2) (E = 3 ГэВ). Для
сравнения показаны значения яркости характеристических линий рентгеновских трубок
и усредненный спектр тормозного излучения рентгеновской трубки
Мощность
излучения
релятивистской
заряженной
частицы,
движущейся по окружности определяются формулой Шотта:
𝑃𝑃 =
2 𝑒𝑒 2 𝑐𝑐𝛽𝛽 4 4
𝛾𝛾 ,
3 𝑅𝑅 2
(6.82)
а потери энергии на СИ за один оборот (с учетом, что один оборот
заряженная частица совершает за период времени 𝑇𝑇 = 2𝜋𝜋𝑅𝑅/𝑐𝑐) составят
4
∆𝑊𝑊 = 𝑃𝑃 ∙ 𝑇𝑇 = 𝜋𝜋
3
𝑒𝑒 2 𝛽𝛽 4 4
𝛾𝛾
𝑅𝑅
(6.83)
Из формулы видно, что потери энергии заряженной частицы на СИ
пропорциональны 𝑇𝑇𝑒𝑒 4 и 1/𝑚𝑚4 . В силу того, что масса электрона на три
порядка меньше, чем масса протона, при прочих равных условиях
мощность СИ для электрона будет больше в 1836 раз.
40
Синхротронное излучение - поляризованное излучение, вектор
напряженности электрического поля 𝐸𝐸�⃗ параллелен плоскости орбиты
вращающихся электронов.
Основное применение СИ нашло в исследованиях физики твердого
тела и используется в качестве источника электронных возбуждений в
широком диапазоне длин волн.
6.3. Взаимодействие гамма – излучения с веществом
Гамма-кванты являются нейтральными частицами, поэтому судить о
том испытал ли гамма-квант взаимодействие проходя через вещество
возможно только по вторичным эффектам. При попадании γ-кванта в
вещество, он также как и заряженные частицы взаимодействует и с
электронной
подсистемой
и
с
ядерной.
Результатом
данного
взаимодействия возможны: полная передача энергии кванта атомному
электрону с последующим возбуждением или ионизацией атома, передача
энергии свободному электрону и рассеяние фотона, либо рождение
электрон-позтронной пары в электромагнитном поле ядра или атомного
электрона. γ-квант также может передать свою энергию и атомному ядру,
что приведет к переходу в возбужденное состояние последнего с
возможностью последующего испускания нуклонов или более тяжелых
частиц (см. главу 5 «Ядерные взаимодействия»). Таким образом, в качестве
вторичных эффектов взаимодействия гамма-квантов с электронной
подсистемой выделяют: фотоэффект, рассеяние фотонов и образование
электрон-позитронной пары.
6.3.1. Фотоэффект
Фотоэффектом называют процесс взаимодействия γ-кванта со
связанным электроном атома, при котором электрону передается вся
энергия фотона. В результате взаимодействия электрон приобретает
энергию равную:
41
𝑇𝑇𝑒𝑒 = ℏ𝜔𝜔 − 𝐼𝐼𝑖𝑖 ,
(6.84)
где ℏ𝜔𝜔 – энергия гамма-кванта, 𝐼𝐼𝑖𝑖 - потенциал ионизации соответствующей
оболочки.
Освободившееся в результате фотоэффекта место на внутренней
оболочке занимает один из электронов с вышележащей оболочки, испуская
при этом квант характеристического рентгеновского излучения (ХРИ).
Таким образом, фотоэффект сопровождается ХРИ, либо конкурирующим с
ХРИ процессом испускания электронов Оже.
В силу выполнения законов сохранения энергии и импульса
фотоэффект может протекать только на связанных электронах атома или
иона. В противном случае, если не учитывать затрат энергии на разрыв
связи электрона с ядром, сохранение полной энергии задавалось бы
выражением
а сохранение импульса
𝐸𝐸𝛾𝛾 = 𝑚𝑚𝑒𝑒 𝑐𝑐 2 �
𝐸𝐸𝛾𝛾
с
=
1
�1−𝛽𝛽 2
𝑚𝑚 𝑒𝑒 𝛽𝛽с
�1−𝛽𝛽 2
− 1�,
.
(6.85)
(6.86)
Сравнивая (6.85) и (6.86) получим соотношение:
𝑚𝑚𝑒𝑒 с �
1
�1−𝛽𝛽 2
− 1� =
𝑚𝑚𝑒𝑒 𝛽𝛽с
�1−𝛽𝛽2
(6.87)
1 − 𝛽𝛽 = �1 − 𝛽𝛽 2
Решению данного уравнения удовлетворяют значения β = 0 и β = 1.
Первое из них соответствует нулевому значению энергии гамма-кванта и
электрона, второе не имеет смысла для частиц с ненулевой массой. Таким
образом, часть энергии фотона всегда передается атомному ядру, за счет
сильной связи между ним и орбитальным электроном.
Методами квантовой электродинамики для релятивистских энергий
было получено выражение для дифференциального сечения фотоэффекта:
42
𝑑𝑑𝜎𝜎
𝑑𝑑Ω
3
𝛽𝛽 3 �1−𝛽𝛽 2 � 𝑆𝑆𝑆𝑆𝑆𝑆 2 𝜃𝜃
= 𝑍𝑍 5 𝛼𝛼 4 𝑟𝑟𝑒𝑒2
2
�1−�1−𝛽𝛽 2 � (1−𝛽𝛽𝛽𝛽𝛽𝛽𝛽𝛽𝛽𝛽 )4
�
2
�1−�1−𝛽𝛽 2 �
3
2(1−𝛽𝛽 2 )2
2−1−1−𝛽𝛽21−𝛽𝛽𝐶𝐶𝑜𝑜𝑠𝑠𝜃𝜃1−𝛽𝛽2с𝑜𝑜𝑠𝑠2𝜑𝜑,
(1 − 𝛽𝛽с𝑜𝑜𝑜𝑜𝑜𝑜) +
(6.88)
где 𝑍𝑍 - порядковый номер атомов среды, α – постоянная тонкой структуры,
𝑟𝑟𝑒𝑒 - классический радиус электрона,
𝜃𝜃 и 𝜑𝜑 - полярный и азимутальный углы
соответственно.
Анализ
𝛽𝛽 → 1
𝛽𝛽 → 0
(6.87)
показывает, что при малых значениях
𝑥𝑥
энергии 𝐸𝐸𝛾𝛾 фотоэлектроны испускаются
(рис. 6.17)
преимущественно
в
направлении электрического вектора 𝐸𝐸�⃗ кванта,
т.е.
Рис. 6.17
перпендикулярно
�⃗ и движения фотона. С ростом энергии
направлениям волнового вектора 𝑘𝑘
𝐸𝐸𝛾𝛾
пространственное
распределение
вытягивается
вперед
ультрарелятивистском
𝜎𝜎
и
в
случае
фотоэлектроны
испускаются
преимущественно в направлении падения
1
7/2
𝐸𝐸𝛾𝛾
𝐼𝐼𝑀𝑀
𝐼𝐼𝐿𝐿
𝐼𝐼𝐾𝐾
Рис. 6.18
фотона.
1
𝐸𝐸𝛾𝛾
𝐸𝐸𝛾𝛾
На
зависимость
(рис.
сечения
6.18)
приведена
фотоэффекта
от
энергии гамма-квантов. Видно, что сечение
резко зависит от энергии фотона, когда
значение 𝐸𝐸𝛾𝛾 сравнимо с величиной одного
из потенциалов ионизации электронных
оболочек атома.
Полное сечение фотоэффекта, полученное интегрированием (6.88), равно
16
5
𝐼𝐼
𝜎𝜎 = 1,09 ∙ 10 𝑍𝑍 � �
𝐸𝐸
43
𝛾𝛾
7/2
,
(6.89)
для случая, когда 𝐼𝐼 ≪ 𝐸𝐸𝛾𝛾 ≪ 𝑚𝑚𝑒𝑒 𝑐𝑐 2 , и
𝜎𝜎 = 1,34 ∙ 10−33
для 𝐸𝐸𝛾𝛾 ≫ 𝑚𝑚𝑒𝑒 𝑐𝑐 2 .
𝑍𝑍 5
𝐸𝐸𝛾𝛾
,
(6.90)
Видно, что для фотоэффекта характерна резкая (~𝑍𝑍 5 ) зависимость от
порядкового номера атомов среды, что существенно увеличивает
вероятность данного эффекта для тяжелых сред, в которых фотоэффект
является основным механизмом поглощения квантов.
Практическое использование фотоэффекта возможно для определения
энергии гамма-излучения. Процедура измерения энергии заключается в
сравнении поглощения фотонов при прохождении поглотителей, имеющих
различные сечения и значения энергетических границ фотопоглощения.
𝜎𝜎
Al
Cu
2,5
10,0
Sn
35,0
Рис. 6.19
Pd
95,0 𝐸𝐸𝛾𝛾 , кэВ
В качестве примера на рис. 6.19 приведены границы наибольшего
фотопоглощения гамма-квантов для некоторых веществ.
6.3.2. Комптоновский эффект
Наряду с фотоэффектом, при котором вся энергия гамма-кванта
передается электрону, взаимодействие γ-излучения с веществом может
приводить к отклонению фотонов от
первоначального направления движения
на некоторый угол θ (рассеянию) и
изменению энергии гамма-кванта (рис.
44
𝑝𝑝ℎ𝜈𝜈
������⃗
Рис. 6.20
𝜃𝜃
𝑝𝑝ℎ𝜈𝜈 ′
��������⃗
𝑝𝑝𝑒𝑒
����⃗
6.20). Данный эффект протекает при энергиях квантов много большей, чем
потенциал ионизации атомных оболочек 𝐸𝐸𝛾𝛾 ≫ 𝐼𝐼𝐾𝐾 , т.е. рассеяние излучения
происходит на свободных заряженных частицах. Детальное изучение
эффекта проведено в 1923 г., в результате которого были обнаружены
следующие эмпирические закономерности комптоновского эффекта:
1. Спектр рассеянного под определенным углом 𝜃𝜃 излучения
содержит кроме излучения с первоначальной длиной волны 𝜆𝜆0 излучение с
длиной волны 𝜆𝜆 > 𝜆𝜆0 .
2. Изменение длины волны ∆𝜆𝜆 = 𝜆𝜆 − 𝜆𝜆0 взаимодействующего гамма-
кванта растет с увеличением угла рассеяния.
3. При фиксированном угле рассеяния, значение ∆𝜆𝜆 не зависит от 𝜆𝜆0 .
4. Величина ∆𝜆𝜆 постоянна для всех рассеивающих веществ, если угол
рассеяния фиксирован.
Значение ∆λ определяется исходя из законов сохранения энергии и
импульса (6.91).
1
ℎ𝜈𝜈 = ℎ𝜈𝜈 ′ + 𝑇𝑇𝑒𝑒 = ℎ𝜈𝜈 ′ + 𝑚𝑚𝑒𝑒 𝑐𝑐 2 �
− 1�
�1−𝛽𝛽 2
�
������⃗
𝑝𝑝ℎ𝜈𝜈 ′ + ����⃗
𝑝𝑝𝑒𝑒
𝑝𝑝ℎ𝜈𝜈 = ��������⃗
(6.91)
Решая систему, можно получить
где 𝛬𝛬 =
ℎ
𝑚𝑚 𝑒𝑒 𝑐𝑐
𝜃𝜃
∆𝜆𝜆 = 𝛬𝛬(1 − cos 𝜃𝜃) = 2𝛬𝛬 sin2 ,
2
(6.92)
= 2,42 ∙ 10−10 см – комптоновская длина волны электрона. Из
анализа (6.92) видно, что значение ∆𝜆𝜆 растет с увеличением угла рассеяния
от 0 при 𝜃𝜃 = 0 до ∆𝜆𝜆 = 2𝛬𝛬 при θ = 𝜋𝜋. При максимальном угле рассеяния
значение ∆λ𝑚𝑚𝑚𝑚𝑚𝑚 = 4,82 ∙ 10−10 см, что сравнимо с длиной волны гаммакванта с энергией 1 МэВ. Для мягкого гамма-излучения длина волны
𝜆𝜆 ≫ ∆λ𝑚𝑚𝑚𝑚𝑚𝑚 и комптоновский эффект в этом случае не существенен.
45
Исходя из решения (6.90) также можно найти значение энергии
рассеянного гамма-кванта ℎ𝜈𝜈 ′ в зависимости от энергии первоначального
гамма-кванта:
Анализ
ℎ𝜈𝜈 ′ =
данного
ℎ𝜈𝜈
ℎ 𝜈𝜈
(1−𝑐𝑐𝑐𝑐𝑐𝑐
1+
𝑚𝑚 𝑒𝑒 𝑐𝑐 2
соотношения
𝜃𝜃 )
позволяет
.
(6.93)
выделить
несколько
граничных случаев:
1. Для значений энергий гамма-кванта ℎ𝜈𝜈 > 𝑚𝑚𝑒𝑒 𝑐𝑐 2 и малых углов 𝜃𝜃, а
также для значений энергий ℎ𝜈𝜈 ≪ 𝑚𝑚𝑒𝑒 𝑐𝑐 2 и любых углов 𝜃𝜃, величина
ℎ𝜈𝜈
𝑚𝑚 𝑒𝑒 𝑐𝑐 2
(1 − 𝑐𝑐𝑐𝑐𝑐𝑐 𝜃𝜃) в (6.93) будет стремиться к нулю и энергия рассеянного
гамма-кванта не будет изменяться ℎ𝜈𝜈 ′ = ℎ𝜈𝜈. Впервые факт отсутствия
изменения длины волны при рассеянии гамма-квантов с ℎ𝜈𝜈 ≪ 𝑚𝑚𝑒𝑒 𝑐𝑐 2 был
обнаружен и исследован Дж.Томпсоном, в честь которого исследованный
эффект получил свое название – эффект Томпсона (Томпсоновское
рассеяние).
2. Для значений энергий гамма-квантов ℎ𝜈𝜈 ≫ 𝑚𝑚𝑒𝑒 𝑐𝑐 2 и больших
углов 𝜃𝜃
ℎ𝜈𝜈
𝑚𝑚 𝑒𝑒 𝑐𝑐 2
𝑚𝑚 𝑐𝑐 2
𝑒𝑒
ℎ𝜈𝜈 ′ = (1−𝑐𝑐𝑐𝑐𝑐𝑐
𝜃𝜃 =
𝜋𝜋
2
𝜃𝜃)
(1 − 𝑐𝑐𝑐𝑐𝑐𝑐 𝜃𝜃) ≫ 1, энергия рассеянного гамма-кванта равна
и не зависит от энергии первоначального гамма-кванта. При
ℎ𝜈𝜈 ′ = 𝑚𝑚𝑒𝑒 𝑐𝑐 2 , а при 𝜃𝜃 = 𝜋𝜋, ℎ𝜈𝜈 ′ =
𝑚𝑚 𝑒𝑒 𝑐𝑐 2
2
.
Энергия рассеянного электрона определяется исходя из разницы
энергий первоначального и рассеянного гамма-квантов и с учетом
подстановки вместо ℎ𝜈𝜈 ′ выражения (6.93) равна:
𝑇𝑇𝑒𝑒 = ℎ𝜈𝜈 − ℎ𝜈𝜈 ′ =
ℎ𝜈𝜈
𝑚𝑚 𝑒𝑒 𝑐𝑐 2
ℎ 𝜈𝜈 (1−𝑐𝑐𝑐𝑐𝑐𝑐 𝜃𝜃 )
1+
.
(6.94)
Дифференциальное сечение комптоновского эффекта описывается
формулой Клейна – Нишины – Тамма:
𝑑𝑑𝜎𝜎
𝑑𝑑Ω
=
1+cos 2 θ
�1
2 [1+ε(1−cos θ)]2
𝑟𝑟e2
46
ε 2 (1−cos θ)2
+ (1+cos 2
θ)[1+ε(1−cos θ)]
�,
(6.95)
ℎ𝜈𝜈
где ε =
𝑚𝑚 𝑒𝑒 𝑐𝑐 2
. При ε → 0 (6.95) сводится к формуле вида
𝑑𝑑𝜎𝜎
=
𝑑𝑑Ω
𝑟𝑟e2
2
(1 + cos 2 θ),
(6.96)
и определяет сечение Томпсоновского рассеяния. Угловое распределение
рассеянных гамма-квантов также зависит от энергии налетающего кванта
(рис. 6.21) и при ε → 0 равновероятно сосредоточено около углов вылета,
равных
0
и
π,
а
при
рассеянные
ε→1
γ-кванты
вылетают
преимущественно под нулевым углом.
Если (6.96) проинтегрировать по 𝑑𝑑Ω, то можно получить формулу для
полного сечения комптоновского эффекта:
𝜎𝜎 = 2π𝑟𝑟e2 �
𝜀𝜀 ≈ 0
180
°
1+ε 2(1+ε)
ε
�
1+2ε
1
− ln(1 + 𝜀𝜀)� +
ε
1
2ε
90°
ln(1 + 2𝜀𝜀) −
0,1
0,4
𝜀𝜀 → ∞
1,0
0°
1+3𝜀𝜀
(1+2ε)2
�. (6.97)
𝑝𝑝ℎ𝜈𝜈
������⃗
270°
Рис. 6.21
При ε → 0 вновь получается формула для полного сечения
Томпсоновского
рассеяния,
константой и равняется 𝜎𝜎 =
где
8πr 2e
3
сечение
взаимодействия
является
. С ростом энергии первоначального γ-
кванта сечение комптоновского рассеяния убывает и при ε ≫ 1 имеет вид
𝜎𝜎 =
π𝑟𝑟e2 1
ε
1
�2 + ln 2𝜀𝜀� ~ 𝐸𝐸 .
𝛾𝛾
47
(6.98)
Если рассматривать рассеяние гамма-излучения не на свободном
электроне, а на атоме, содержащем Z электронов, то для длин волн λ ≪ rk
– радиуса К – оболочки атома и при ε ≫ 1 полное сечение комптоновского
рассеяния на атоме будет зависеть от Z:
Комптоновский
𝜎𝜎 𝑎𝑎 =
π𝑟𝑟e2 1
ε
эффект
𝑍𝑍
�2 + ln 2𝜀𝜀� ~ 𝐸𝐸 .
может
(6.99)
𝛾𝛾
наблюдаться
не
только
на
неподвижном, но и на движущемся электроне. Формулу для энергии
рассеянного гамма-кванта на движущемся электроне можно получить из
(6.100):
𝐸𝐸𝛾𝛾′ =
𝐸𝐸𝛾𝛾 (1−𝛽𝛽 cos 𝜃𝜃1 )
𝐸𝐸 𝛾𝛾
,
(6.100)
1−𝛽𝛽 cos 𝜃𝜃2 + (1−cos 𝜃𝜃 )
𝐸𝐸 𝑒𝑒
где 𝜃𝜃1 - угол между импульсами ����⃗
𝑝𝑝𝛾𝛾 и 𝑝𝑝
����⃗,
�����⃗
𝑒𝑒 𝜃𝜃2 - угол между импульсами 𝑝𝑝
𝛾𝛾 ′ и
����⃗,
𝑝𝑝𝛾𝛾 и 𝑝𝑝
�����⃗
𝑝𝑝𝑒𝑒 𝜃𝜃 - угол между ����⃗
𝛾𝛾 ′ (рис. 6.22). Из
формулы видно, что при рассеянии на
движущемся электроне, энергия фотона
𝑝𝑝ℎ𝜈𝜈 ′
��������⃗
может возрастать, достигая максимального
значения при движении фотона на встречу
электрону (𝜃𝜃1 = π) и рассеянии назад
(𝜃𝜃2 = 0, 𝜃𝜃 = π). Так при рассеянии мягких
фотонов
на
𝜃𝜃2
𝑝𝑝ℎ𝜈𝜈
������⃗
𝜃𝜃
ультрарелятивистских
𝜃𝜃1
Рис. 6.22
𝑝𝑝𝑒𝑒
����⃗
электронах энергия рассеянного гамма-кванта может оказаться сравнимой
с энергией электрона (обратный комптоновский эффект).
6.3.3. Эффект образования пар
Эффект образования пар (ЭОП) заключается в образовании электрон –
позитронной
пары
при
взаимодействии
гамма-кванта
с
энергией
ℎ𝜈𝜈 ≥ 2𝑚𝑚𝑒𝑒 𝑐𝑐 2 с электрическим полем ядра или атомных электронов. Данный
эффект является пороговым и может происходить согласно законам
48
сохранения энергии и импульса только в присутствии третьего тела.
Убедимся в этом. В отсутствии третьего тела законы сохранения энергии и
импульсы выглядели бы следующим образом:
�
𝐸𝐸𝛾𝛾 = 𝐸𝐸𝑒𝑒 + + 𝐸𝐸
=
𝑒𝑒 −
𝑚𝑚 𝑒𝑒 + 𝑐𝑐 2
�1−𝛽𝛽
+
2
pγ = p
����⃗
������⃗
������⃗
𝑒𝑒 + + p
𝑒𝑒 −
𝑚𝑚 𝑒𝑒 − 𝑐𝑐 2
�1−𝛽𝛽 2
(6.101)
Тогда значение импульса с одной стороны
а с другой стороны
����⃗�
�p
γ =
𝐸𝐸𝛾𝛾
с
=
𝑚𝑚 𝑒𝑒 + 𝑐𝑐
�1−𝛽𝛽 2
+
𝑚𝑚 𝑒𝑒 − 𝑐𝑐
�1−𝛽𝛽 2
����⃗�
������⃗|
������⃗|
�p
γ = |p
𝑒𝑒 + + |p
𝑒𝑒 − =
,
(6.102)
𝑚𝑚 𝑒𝑒 + 𝛽𝛽с
�1−𝛽𝛽
+
2
𝑚𝑚 𝑒𝑒 − 𝛽𝛽с
�1−𝛽𝛽 2
.
(6.103)
Сравнивая правые части (6.100) и (6.101) получается неравенство
����⃗�
������⃗|
������⃗|,
�p
γ > |p
e + + |p
e − что является невозможным, поскольку данные вектора
образуют треугольник. Следовательно, в записи законов сохранения
энергии и импульса необходимо учитывать энергию отдачи и импульс
отдачи третьей частицы, в поле которой образуется электрон –
позитронная пара.
Пороговая энергия гамма-кванта может меняться в зависимости от
массы третьей частицы. Так в поле любого ядра образование пары частиц
требует наличия фотона с энергией равной 1,022 МэВ, тогда как в поле
электрона энергия фотона должна быть 2,044 МэВ (4𝑚𝑚𝑒𝑒 𝑐𝑐 2 ), поскольку
энергия отдачи электрона во много раз больше энергии отдачи ядра.
Дифференциальное
сечение
эффекта
образования
пар
имеет
различные зависимости в разных энергетических интервалах гаммаквантов и не может быть однозначно описано теоретически. Поэтому в
данном разделе приведем лишь формулу для полного сечения ЭОП в
случае, когда ℎ𝜈𝜈 ≫ 𝑚𝑚𝑒𝑒 𝑐𝑐 2 :
𝜎𝜎 =
28
9
𝑍𝑍 2 𝛼𝛼𝑟𝑟e2 �ln
2𝐸𝐸𝛾𝛾
𝑚𝑚 𝑒𝑒
49
𝑐𝑐 2
−
109
2𝐸𝐸𝛾𝛾
� ~𝑍𝑍 2 ln 𝑚𝑚
42
𝑒𝑒 𝑐𝑐
2
.
(6.104)
Сечение образования электрон-позитронных пар в поле электрона
примерно в 1000 раз меньше, чем в поле ядра, в особенности, если
сравнение проводится для малых энергий гамм-квантов и больших
значений Z.
Если
обладает
γ-квант
большой
энергией,
то
компоненты
образующейся пары в большинстве случаев испускаются вдоль движения
фотона под углом, равным отношению 𝜃𝜃 =
𝑚𝑚 𝑒𝑒 𝑐𝑐 2
𝐸𝐸𝛾𝛾
.
6.3.4. Ослабление гамма-излучения в веществе
Таким образом, при взаимодействии гамма-излучения с веществом,
без
учета
ядерных
реакций,
протекают
три
основных
эффекта:
фотоэффект, комптоновский эффект и эффект образования пар. В случае
выполнения порогового условия для энергии гамма-кванта в ЭОП все три
эффекта могут происходить одновременно с разной вероятностью.
Вероятность каждого из них определяется сечением, а вероятность
взаимодействия гамма-излучения с веществом определяется суммарным
сечением взаимодействия
где 𝜎𝜎фэ ~
𝑍𝑍 5
7/2
Е𝛾𝛾
, 𝜎𝜎кэ ~
1
Е𝛾𝛾
𝜎𝜎Σ = 𝜎𝜎фэ + 𝜎𝜎кэ + 𝜎𝜎эоп ,.
и 𝜎𝜎эоп ~𝑍𝑍 2 ln
2𝐸𝐸𝛾𝛾
𝑚𝑚 𝑒𝑒 𝑐𝑐 2
(6.105)
. На рис. 6.23 показаны характерные
зависимости сечений трех эффектов и суммарного сечения взаимодействия
гамма-излучения с веществом в зависимости от энергии фотонов в
единицах 𝑚𝑚𝑒𝑒 𝑐𝑐 2 на примере свинца.
50
𝜎𝜎
𝜎𝜎фэ
𝜎𝜎кэ
10-1
𝐸𝐸1
100
𝐸𝐸2
101
𝜎𝜎эоп
𝜎𝜎Σ
102
𝐸𝐸𝛾𝛾
𝑚𝑚𝑒𝑒 𝑐𝑐 2
Рис. 6.23
Зависимость является типичной для всех веществ. В области малых
энергий 𝐸𝐸𝛾𝛾 < 𝐸𝐸1 (𝐸𝐸1 определяется из условий равенства (𝜎𝜎фэ (𝐸𝐸1 ) =
σкэ (𝐸𝐸1 )) преобладает фотоэффект. В области промежуточных значений
энергии E1 < 𝐸𝐸γ < E2 (𝐸𝐸2 определяется из условий равенства (𝜎𝜎кэ (𝐸𝐸2 ) =
𝜎𝜎эоп (𝐸𝐸2 )) - комптоновский эффект. При 𝐸𝐸𝛾𝛾 > 𝐸𝐸2 превалирует эффект
образования пар. Значения энергий 𝐸𝐸1 и 𝐸𝐸2 обычно различны для разных
сред. Например, для алюминия 𝐸𝐸1 =0,05 МэВ, 𝐸𝐸2 =15 МэВ, а для свинца 0,5
и 5 МэВ соответственно.
В результате фотоэффекта, комптоновского эффекта и эффекта
образования пар гамма излучение может поглощаться либо рассеиваться
при прохождении через различные среды, что приводит к ослаблению
пучка гамма-квантов. Если предположить, что на мишень c концентрацией
атомов n падает 𝑁𝑁0 фотонов, а в слой 𝑑𝑑𝑑𝑑 проникает 𝑁𝑁(𝑥𝑥) (рис. 6.24), то
51
число фотонов, испытавших взаимодействие и выбывших из потока, будет
равно
𝑑𝑑𝑑𝑑 = −𝑁𝑁(𝑥𝑥) ∙ 𝑛𝑛 ∙ 𝜎𝜎 ∙ 𝑑𝑑𝑑𝑑.
(6.106)
𝑁𝑁 = 𝑁𝑁0 𝑒𝑒 −𝜎𝜎𝜎𝜎𝜎𝜎 = 𝑁𝑁0 𝑒𝑒 −𝜇𝜇𝜇𝜇 ,
(6.107)
Решение данного уравнения приводит к закону ослабления гаммаизлучения в веществе вида
где 𝑁𝑁 - число гамма-квантов прошедших мишень без взаимодействия,
𝜇𝜇 = 𝜎𝜎𝜎𝜎 – коэффициент ослабления γ-излучения в веществе.
𝑁𝑁0
𝑥𝑥
𝑑𝑑𝑑𝑑
𝑁𝑁
Д
Рис. 6.24
Данный закон определяет число гамма-квантов, прошедших через
мишень толщиной x без взаимодействия. Число провзаимодействовавших
квантов определяется разницей между числом падающих и прошедших
мишень гамма-квантов
𝐹𝐹 = 𝑁𝑁0 − 𝑁𝑁 = 𝑁𝑁0 (1 − 𝑒𝑒 −𝜇𝜇𝜇𝜇 ),
(6.108)
а вероятность взаимодействия определяется как отношение числа
провзаимодействовавших гамма-квантов к числу упавших на мишень и
выражается как
𝑃𝑃 =
𝑁𝑁0 −𝑁𝑁
𝑁𝑁0
= (1 − 𝑒𝑒 −𝜇𝜇𝜇𝜇 ).
52
(6.109)
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Мухин К.Н. Экспериментальная ядерная физика. В 2 кн. Кн. 1 Физика
атомного ядра / К.Н. Мухин. М. : Энергоатомиздат, 1993. 316 с.
2. Широков Ю.М. Ядерная физика / Ю.М. Широков, Н.П. Юдин. М. :
Наука, 1980. 727 с.
3. Голубев Б.П. Дозиметрия и защита от ионизирующих излучений. Изд.
3-е перераб. и доп. Под ред. Е.Л.Столяровой. Учебник для вузов. /
Б.П.Голубев. М. : Атомиздат, 1976. 504 с.
53