Движение заряженных частиц в магнитном поле
реклама
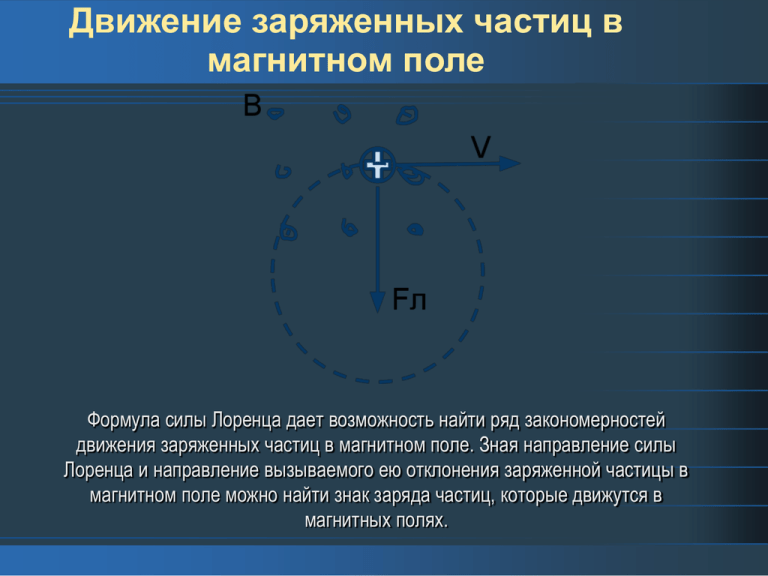
Движение заряженных частиц в магнитном поле Формула силы Лоренца дает возможность найти ряд закономерностей движения заряженных частиц в магнитном поле. Зная направление силы Лоренца и направление вызываемого ею отклонения заряженной частицы в магнитном поле можно найти знак заряда частиц, которые движутся в магнитных полях. Для вывода общих закономерностей будем полагать, что магнитное поле однородно и на частицы не действуют электрические поля. Если заряженная частица в магнитном поле движется со скоростью v вдоль линий магнитной индукции, то угол α между векторами v и В равен 0 или π. Тогда сила Лоренца равна нулю, т. е. магнитное поле на частицу не действует и она движется равномерно и прямолинейно. Направление, в котором закручивается спираль, определяется знаком заряда частицы. Если скорость v заряженной частицы составляет угол α с направлением вектора В неоднородного магнитного поля, у которого индукция возрастает в направлении движения частицы, то r и h уменьшаются с увеличением В. На этом основана фокусировка заряженных частиц в магнитном поле. Движение заряженных частиц в однородном электрическом поле. Если частица, обладающая зарядом е, движется в пространстве, где имеется электрическое поле с напряжённостью E то на неё действует сила eE. Если, кроме электрического, имеется магнитное поле, то на частицу действует ещё сила Лоренца, равная e[uB] , где u - скорость движения частицы относительно поля, B - магнитная индукция. Если зазор между пластинами мал по сравнению с их длиной, то краевыми эффектами можно пренебречь и считать электрическое поле между пластинами однородным. В рассматриваемом случае на заряженные частицы действует только сила со стороны электрического поля, которая при выбранном направлении координатных осей целиком направлена по оси Y. Выводы: Магнитное поле относительно — его индукция зависит от системы отсчета. Отсюда можно сделать вывод, что относительно и электрическое поле. Рекомендации Предложите одну или несколько стратегий Дайте обзор ожидаемых результатов Обозначьте дальнейшие шаги Распределите различные задачи