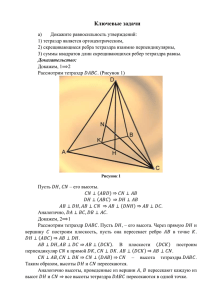
ТЕТРАЭДР Определение Тетраэдр — многогранник с четырьмя треугольными гранями, в каждой из вершин которого сходятся по 3 грани. У тетраэдра 4 грани, 4 вершины и 6 рёбер.Слово «тетраэдр» образовано из двух греческих слов: tetra-«четыре» и hedra«основание»,«грань». Построение тетраэдра Изображают обычно тетраэдр как четырехугольник с диагоналями, одну из которых (соответствующую невидимому ребру) изображают пунктирно. D С А В Тетраэдр Два ребра тетраэдра, которые не имеют общих вершин, называются противоположными. Например, АD и ВС , ВD и АС, АВ и СD. D C A H B DАВС – тетраэдр А, В, С, D – вершины АВС – основание АD, ВD, СD, АС, АВ, ВС– ребра DH – высота тетраэдра Определения медианы, бимедианы(средние линии) и высоты тетраэдра Отрезок, соединяющий вершину тетраэдра с точкой пересечения медиан противоположной грани, называется его медианой, опущенной из данной вершины. Отрезок, соединяющий середины скрещивающихся рёбер тетраэдра, называется его бимедианой, соединяющей данные рёбра. Отрезок, соединяющий вершину с точкой противоположной грани и перпендикулярный этой грани, называется его высотой, опущенной из данной вершины. Объем тетраэдра Объем тетраэдра — равен дроби в числителе которой корень квадратный из двух в знаменателе двенадцать, помноженной на куб длины ребра тетраэдра. h (V - объем тетраэдра, a - ребро тетраэдра) Площадь Площадь тетраэдра — равна сумме площадей его граней и площади основания. Грани тетраэдра – треугольники. Площадь равна: Высота тетраэдра Высота тетраэдра — равна корню квадратному из двух третих, помноженному на длину ребра тетраэдра (h - высота тетраэдра, a - ребро тетраэдра) Типы тетраэдров Равногранный тетраэдр – это тетраэдр, у которого все грани – равные между собой треугольники. Ортоцентрический тетраэдр – это тетраэдр, у которого все высоты, опущенные из вершин на противоположные грани, пересекаются в одной точке. Прямоугольный тетраэдр – это тетраэдр, у которого все ребра, прилежащие к одной из вершин, перпендикулярны между собой. Правильный тетраэдр – это тетраэдр, у которого все грани — равносторонние треугольники. Соразмерный тетраэдр, бивысоты которого равны. Инцентрический тетраэдр –это тетраэдр, у которого отрезки, соединяющие вершины тетраэдра с центрами окружностей, вписанных в противоположные грани, пересекаются в одной точке. Правильный тетраэдр • Тетраэдр, все четыре грани которого — равные правильные треугольники, называется правильным тетраэдром . • Правильный тетраэдр — это частный случай правильной треугольной пирамиды. Правильный тетраэдр Все четыре правильные Если длину обозначить Площадь полной поверхности грани правильного тетраэдра – треугольники. ребра правильного тетраэдра a, то можно вычислить: 3a 2 Радиус описанной сферы 6 a 4 Объем 2 3 a 12 Угол наклона ребра Высоту 6 a 3 Угол наклона грани arctg 2 2 Телесный угол при вершине 23 arccos 27 Радиус вписанной сферы 6 a 12 arctg 2 Прямоугольный тетраэдр Тетраэдр , у которого в одной вершине сходятся три прямых угла называют прямоугольным. Такой тетраэдр можно получить, разрезав куб. Свойство тетраэдра Каждая его вершина является вершиной трех треугольников. А значит, сумма плоских углов при каждой вершине будет равна 180º. В правильный тетраэдр можно вписать октаэдр. Правильный тетраэдр можно вписать в икосаэдр, притом, четыре вершины тетраэдра будут совмещены с четырьмя вершинами икосаэдра. Правильный тетраэдр можно вписать в куб двумя способами, притом четыре вершины тетраэдра будут совмещены с четырьмя вершинами куба. Где используется тетраэдр? Tetra Classic® — картонная упаковка в форме тетраэдра для хранения молока, созданная в 1950 году компанией Tetra Pak. С 1959 года поставлялась и широко использовалась в СССР, где эти упаковки обычно назывались «пирамидками» или «треугольными пакетами». Пирамидки были двух основных размеров: большая (для молока и кефира) и поменьше (для сливок). Они были оформлены по-разному в зависимости от вида продукта. Оказалось, что на конвейере удобно склеивать подобные тетраэдры, отрезая заготовки для них от картонного “шланга”. Тетраэдры в живой природе Некоторые плоды, находясь вчетвером на одной кисти, располагаются в вершинах тетраэдра, близкого к правильному. Такая конструкция обусловлена тем, что центры четырёх одинаковых шаров, касающихся друг друга, находятся в вершинах правильного тетраэдра. Поэтому похожие на шар плоды образуют подобное взаимное расположение. Например, таким образом могут располагаться грецкие орехи. Тетраэдры в строительстве Тетраэдр образует жёсткую, статически определимую конструкцию. Тетраэдр, выполненный из стержней, часто используется в качестве основы для пространственных несущих конструкций пролётов зданий, перекрытий, балок, ферм, мостов и т. д. Стержни испытывают только продольные нагрузки. Уголковый отражатель Уголковый отражатель — устройство в виде прямоугольного тетраэдра со взаимно перпендикулярными отражающими плоскостями. Излучение, попавшее в уголковый отражатель, отражается в строго обратном направлении. Используется:для точного измерения расстояний (для лазерной локации Луны, ИСЗ; топосъемке, строительстве); для возврата излучения точно назад (катафот, радиоэлектронная борьба). Тетраэдры в микромире Молекула метана СН4 Молекула аммиака NH3 Алмаз C — тетраэдр с ребром равным 2,5220 ангстрем Флюорит CaF2, тетраэдр с ребром равным 3, 8626 ангстрем Сфалерит, ZnS, тетраэдр с ребром равным 3,823 ангстрем Комплексные ионы [BF4] -, [ZnCl4]2-, [Hg(CN)4]2-, [Zn(NH3)4]2+ Силикаты, в основе структур которых лежит кремнекислородный тетраэдр [SiO4]4- Lipton tea & тетраэдр Чайная компания Lipton для разнообразия формы пакетиков для чая теперь выпускает их в виде тетраэдра Головоломка Существуют головоломки в виде тетраэдра. Изображение тетраэдра Пусть A0B0C0D0 – произвольный тетраэдр, A, B, C и D – параллельные проекции его вершин на плоскость изображений (π). Отрезки AB, BC, CA, AD, BD, CD служат сторонами и диагоналями четырёхугольника ABCD. Фигура, образованная из этих отрезков (или любая другая фигура, подобная ей), является изображением тетраэдра A0B0C0D0 . Фигура, состоящая из сторон и диагоналей любого (выпуклого или невыпуклого) четырёхугольника, является изображением тетраэдра при соответствующем выборе плоскости изображений и направления проектирования. На этих рисунках невидимые рёбра изображены штриховыми линиями. А М В N D С Точки М и N – середины ребер АВ и АС тетраэдра АВСD. Докажите, что прямая МN параллельна плоскости ВСD. Какие многоугольники могут получиться в сечении ? Тетраэдр имеет 4 грани В сечениях могут получиться: Треугольники Четырехугольники Объясните, как построить сечение тетраэдра DABC плоскостью, проходящей через точки M,N,K D Найдите M А K N B C периметр сечения, если M, N, K – середины ребер и каждое ребро тетраэдра равно а. Объясните, как построить сечение тетраэдра DABC плоскостью, проходящей через точки M,N,K D Найдите периметр сечения, если M, N, K – середины ребер и каждое ребро тетраэдра равно а. K N А M B C Объясните, как построить сечение тетраэдра DABC плоскостью, проходящей через точки M,N,K D Найдите K E А периметр сечения, если M, N, K – середины ребер и каждое ребро тетраэдра равно а. C M B N Объясните, как построить сечение тетраэдра DABC плоскостью, проходящей через точки M,N,K MN ║ AC D K E А C M N B Тетраэдр D Постройте сечение тетраэдра плоскостью, проходящей через точку М параллельно (АВС). М Р К А С В Д Постройте сечение тетраэдра плоскостью, проходящей через точки Т, Р , О Р О Х В А М Т С Через середины ребер АВ и ВС тетраэдра SАВС проведена плоскость параллельно ребру SВ. Докажите, что эта плоскость пересекает грани SАВ и SВС по параллельным прямым. S Е К Дано: SАВС –тетраэдр, МА=МВ, ВN=NC, А С М N В М , N , ВS || , ABS КM , BCS ЕN . Доказать : КM || ЕN . Изобразите тетраэдр DABC и на ребрах DB, DC, и BC отметьте соответственно точки М, N и К. Постройте точку пересечения прямой КN и плоскости ABD. D M • Дано : DABC тетраэдр, М DВ, N • А N DC , K BC . Построить : точку М 1. Условие : М 1 KN АВD . С Решение : 1. NK DBC , DB DBC . В •K • M1 2. Допустим, NK || DB , тогда NK || АВD по признаку , а это противоречит условию. Значит, NK DB. 3. DB АВD , NK DB , тогда NK АВD М 1. • Задача1. На рёбрах AB, BD и CD тетраэдра ABCD отмечены точки M,N и P. Построить сечение тетраэдра плоскостью MNP. Решение. Построим сначала прямую, по которой плоскость MNP пересекается с плоскостью грани ABC. Точка М является общей точкой этих плоскостей. Для построения ещё одной общей точки продолжим отрезки NP и BC до их пересечения в точке Е, которая и будет второй общей точкой плоскостей MNP и ABC. ДОМАШНЕЕ ЗАДАНИЕ D Задача № 1 А Постройте точку пересечения прямой АВ с плоскостью MNK. B M N K D • Задача № 2 • Постройте сечение тетраэдра плоскостью, проходящей через точки А, В и С; С Є MND. С B M А N K D Задача № 3 Постройте точку пересечения прямой АВ с плоскостью MDK. А K M B N D А Задача №4 Постройте сечение тетраэдра плоскостью, проходящей через точки А, В и С; В Є NDK. C B K M N