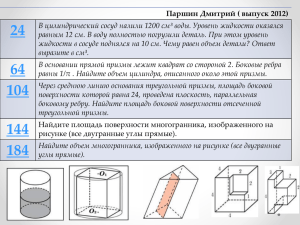
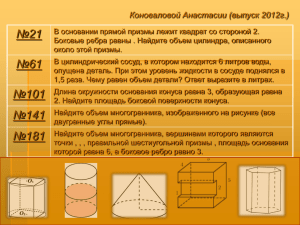
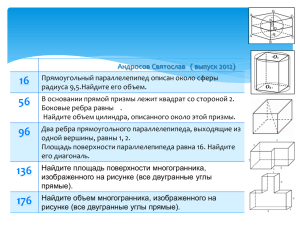
Понятие многогранника. Призма. Урок по геометрии для 10 класса Цели урока: • ввести понятие многогранника, призмы и их элементов; • рассмотреть виды призмы, ввести понятие площади поверхности призмы; • вывести формулу для вычисления площади поверхности прямой призмы Ход урока: • Объяснение нового материала • Многогранник – поверхность, составленная из многоугольников и ограничивающая некоторое геометрическое тело. Тетраэдр Параллелепипед Октаэдр • Многоугольники, из которых составлен многогранник, называются его гранями. • Гранями тетраэдра и октаэдра являются треугольники. А гранями параллелепипедапараллелограммы. • Стороны граней называются ребрами, а концы ребервершинами многогранника. • Отрезок, соединяющий две вершины, не принадлежащие одной грани, называется диагональю многогранника. • Плоскость, по обе стороны от которой имеются точки многогранника, называется секущей плоскостью, а общая часть многогранника и секущей плоскостисечением многогранника. • Многогранники бывают выпуклые и невыпуклые. • Многогранник называется выпуклым, если он расположен по одну сторону от плоскости каждой его грани. • Многогранник , составленный из двух равных многоугольников А1А2…Аn и В1В2…Вn, расположенных в параллельных плоскостях, и n параллелограммов, называется призмой. • Многоугольники А1А2…Аn и В1В2…Вn называются основаниями, а параллелограммы - боковыми гранями призмы. Отрезки А1В1, А2В2, АnВn называются боковыми ребрами. • Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания, называется высотой призмы. • Если боковые ребра призмы перпендикулярны к основаниям, то призма называется прямой, в противном случае – наклонной. • Прямая призма называется правильной, если ее основанияправильные многоугольники. • Площадью полной поверхности призмы называется сумма площадей всех ее граней, а площадью боковой поверхности призмы- сумма площадей ее граней. •S полн =S +S бок осн • Теорема: • Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту • Доказательство: • Боковые грани прямой призмыпрямоугольники, основания которых- стороны основания призмы, а высоты равны высоте h призмы. Площадь боковой поверхности призмы равна сумме площадей указанных прямоугольников, т.е. равна сумме произведений сторон основания на высоту h. Вынося множитель h за скобки, получим в скобках сумму сторон основания призмы, т.е. его периметр Р. Итак, Sбок = Р h. Теорема доказана. • Решение задач (применение знаний в стандартной ситуации) Устно: № 218 В тетради и на доске: №№ 219, 223, 229 (а), 230 • Подведение итогов, домашнее задание П.П. 25-27 учить №№ 220, 229 (б, в), 231