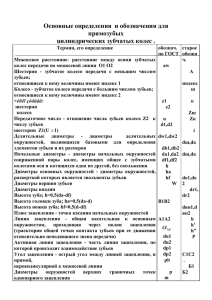
1. Зубчатые механизмы 1.1 Возможности по преобразованию вида движения, скорости, достоинства, недостатки зубчатых механизмов. Механизм - искусственно созданная система тел, предназначенная для преобразования движения одного из них или нескольких в требуемые движения других тел. Зубчатые механизмы – механизмы, в которых движение передается за счет зацепления зубьев. Включают в себя зубчатые колеса различной формы, зубчатые рейки, образующие вращательные или поступательные пары. Зубчатые механизмы – это самый распространенный вид механизмов. На вышеприведенном рисунке изображены два вида передачи, реализованные на зубчатом механизме. Цилиндрическая передача изменяет скорость и направление вращения, сохраняя вид движения (вращение), а реечная передача изменяет вид движения (вращательное и поступательное). Достоинства зубчатых механизмов: - высокая нагрузочная способность; - строго постоянное передаточное отношение; - высокий КПД (до 0,97…0,98 в одной ступени); - большая передаваемая мощность на единицу массы; - небольшие силы давления на валы и опоры; - простота обслуживания; - надежность и долговечность. Недостатки зубчатых механизмов: - сложность и высокая точность изготовления и сборки, отсюда высокая стоимость; -невозможность плавного бесступенчатого регулирования скорости вращения ведомого звена; - высокая жёсткость, не позволяющая компенсировать динамические нагрузки - шум при работе, особенно при работе на больших окружных скоростях. 1.2 Классификация зубчатых передач; возможности, достоинства, недостатки разных видов зубчатых передач. Зубчатыми передачами называются механизмы с высшими кинематическими парами, в состав которых входят зубчатые колеса, рейки или секторы – звенья, снабженные профилироваными выступами или зубьями. Шестерня – меньшее из пары зубчатых колес. Колесо – большее. «Зубчатое колесо» – термин, применяющийся как к большому, так и к малому колесу зубчатой передачи. Индексы «1» и «2» присваивают соответственно параметрам шестерни и колеса. Зацепление зубчатых колес кинематически представляет собой качение без скольжения друг по другу двух поверхностей, называемых начальными (для конических – конусы, для цилиндрических – цилиндры). Точка качения определяется как полюс зацепления. Зубчатые передачи бывают простые и сложные. Простая зубчатая передача – трехзвенные механизм, состоящий из двух зубчатых колес и стойки, в котором зубчатые колеса образуют между собой высшую пару, со стойкой - низшие (поступательные или вращательные). Классификация зубчатых передач: 1) По числу пар зацепляющихся колес: – одно– , двух– , многоступенчатые. Позволяют значительно менять передаточное отношение, а также распределять передачу на разные потребители с одинаковыми или разными требующимися характеристиками ( скорость, момент). 2) По взаимному расположению осей: – цилиндрические с параллельными осями , – конические с пересекающимися осями – могут быть прямозубые, косозубые, с круговым зубом. – червячные и винтовые со скрещивающимися в пространстве осями. Передачи со скрещивающимися или пересекающимися осями позволяют при передаче менять ее направление ( под углом). 3) По расположению зубьев относительно образующих начальной поверхности колеса: – прямозубые – колеса (передачи), направление каждого зуба которых совпадает с образующей начальной поверхности (цилиндра или конуса). Наиболее просты в изготовлении. При использовании непрямозубых колёс повышается плавность и бесшумность работы и увеличивается нагрузочная способность передачи, но одновременно появляется осевая сила (недостаток). – косозубые – зубчатые колеса, направление каждого зуба которых составляет некоторый постоянный угол с образующей начальной поверхности. – шевронные – колеса, зубчатый венец которых образуется из двух рядов косых зубьев противоположного направления (вторым рядом компенсируется недостаток однорядной косозубой шестерни – осевая сила) – с круговым зубом Зацепление может быть внешним и внутренним. Отдельный вид зубчатых передач – реечные, преобразует вращательное движение в поступательное, или наоборот. Червячная передача Реечная передача Передачи с эвольвентным профилем зубьев являются достаточно распространенными, в связи с тем, что оно малочувствительно к отклонениям межосевого расстояния, не нарушается правильность зацепления; а также профиль зубьев инструмента для нарезания эвольвентных зубчатых колес может быть прямолинейным, что делает изготовление и контроль инструмента колес достаточно простым. Одним инструментом можно нарезать колеса с разным числом зубьев. Траектория точки контакта эвольвентных профилей зубьев является прямая линия. 4) По конструктивному выполнению корпуса: – открытые (не имеют защиты от попадания пыли и грязи) – закрытые (имеют жесткий корпус, работают в масляной ванне) 5) По характеру работы: – реверсивные (поочередное изменение направления движения ведущего звена на противоположное) – нереверсивные 6) По величине окружной скорости: – тихоходные (до 3 м/с) – средних скоростей (3—15 м/с) – быстроходные (свыше 15 м/с) 1.3 Геометрические параметры цилиндрических прямозубых колес и передач. Передаточное отношение (число) зубчатых передач. Рисунок 1.3.1 Элементы зубчатых колес На рис.1.3.1 представлены элементы зубчатых колес, находящихся в зацеплении, в плоскости, перпендикулярной к оси вращения. По высоте снаружи зубья ограничены окружностью выступов диаметром dа, изнутри – окружностью впадин диаметром df. Боковые поверхности полного профиля зуба очерчены эвольвентами противоположных ветвей. Эвольвента - траектория произвольной точки прямой, перекатывающейся без скольжения по окружности, называемой основной. Положительная ветвь эвольвенты получается при перекатывании производящей прямой против хода часовой стрелки, отрицательная – по ходу часовой стрелки. С увеличением радиуса основной окружности до бесконечности (зубчатая рейка) эвольвента превратится в прямую. Часть бокового профиля зуба очерчивается по переходной кривой, служащей плавным переходом от эвольвенты к окружности впадин. Наличие переходной кривой делает зуб более прочным у основания. При зацеплении одного колеса с другим появляется начальная окружность радиусом rw. Это окружность одного зубчатого колеса, перекатывающаяся без скольжения по окружности (поверхности) второго из зацепляющихся колес. Расстояние между одноименными профилями соседних зубьев по дуге окружности называется окружным шагом и обозначается pt. Значение этого параметра по начальным окружностям должно быть одинаковым у находящихся в зацеплении колес. Пользуясь шагом зацепления, можно выразить длину любой окружности колеса, умножив шаг на число зубьев z: ptz = πdt, где t – индекс соответствующей окружности, например, pa, da или pf, df. Величина pt - несоизмеримое число, так как в правую часть условия входит число π. Это затрудняет выбор размеров колес при их проектировании и изготовлении. Поэтому основным параметром принят не шаг, а отношение его к числу π. Эта величина называется модулем зацепления mt: mt = pt/π. |мм| Шаг и модуль имеют индекс той окружности, по которой они измерены. Величины модулей для снижения номенклатуры и унификации режущего и контролирующего инструмента стандартизированы. Чаще всего согласно стандартам, ограничиваются следующими значениями модуля (в миллиметрах): 0,05; 0,06; 0,08; 0,1; 0,12; 0,15; 0,20; 0,25; 0,3; 0,5; 0,6; 0,8; 1,0; 1,25; 1,5; 2,0; 2,5; 3,0; 4,0; 5,0. Окружность, по которой модуль имеет расчетное стандартное значение, называется делительной. Диаметр ее обозначается d, она является базовой для определения элементов зубьев и их размеров. Шаг и модуль по делительной окружности обозначают соответственно р и m. Диаметр делительной окружности d = mz. Для наиболее распространенных неисправленных по высоте (нулевых) колес начальная и делительные окружности совпадают и передаточное отношение для пары таких колес будет равно i12 = ω1/ω2 = = d2/d1 = z2/z1 Помимо шага по дуге окружности различают и угловой шаг (центральный угол, соответствующий шагу по дуге). За время контакта одной пары зубьев колесо повернется на угол перекрытия. Для обеспечения непрерывности передачи движения от ведущего к ведомому колесу необходимо, чтобы до выхода из контакта данной пары зубьев в зацепление вступила очередная пара зубьев. Это условие будет соблюдаться, если угловой шаг колеса меньше угла перекрытия. Отношение угла перекрытия к угловому шагу, называют коэффициентом перекрытия зубчатой передачи εγ. Допустимым считается значение εγ ≥ 1,2. Часть зуба высотой ha, заключенную между окружностью выступов и делительной окружностью, называют головкой зуба, а часть зуба высотой hf, заключенную между делительной окружностью и окружностью впадин, – ножкой зуба. Основные геометрические параметры зубчатого колеса: – диаметры выступов da, – диаметр впадин df, – общая высота зуба h, – высота головки ha, – высота ножки hf, – толщина зуба s, – ширина впадин между зубьями е выражаются через основной параметр зубчатой передачи – модуль m, по ГОСТ 9587-68. Высота головки зуба ha = ha∙m, где ha – коэффициент высоты головки, который в соответствии со стандартом равен единице (ha = 1), а высота головки равна модулю (ha = m). Высота ножки зуба hf = (ha + c)m, где с = сm – величина радиального зазора (см. рис. 1.3.1) между зубьями колес, находящихся в зацеплении; с* – коэффициент радиального зазора, который зависит от величины модуля: с* = 0,5 при m ≤ 0,5 мм, с = 0,35 при 0,5 < m < 1 мм и с = 0,25 при m ≥ 1 мм. Высота зуба h = ha + hf = m(2 + c*). Диаметры окружности выступов и впадин равны соответственно da = d + 2ha = m(z + 2) и df = d – 2hf = m(z – 2 – 2c*). Ширину зубчатого венца b принимают равной 2 … 6 модулям. Окружная толщина s зуба по делительной окружности s = p/2 = πm/2. Боковой зазор в зубчатом зацеплении устанавливается в зависимости от принятого вида сопряжения колес. Траектория точек контакта пары зубьев во время зацепления у эвольвентных колес называется линией зацепления. Она является общей нормалью к боковым профилям зубьев. Угол между линией зацепления и перпендикуляром к межосевому расстоянию называют углом зацепления α, обычно α = 20°. При изменении межосевого расстояния линия зацепления изменяет свое положение. Изменяется угол зацепления, но передаточное отношение не нарушается. Рис. 1.3.2 Чем меньше зубьев имеют колеса, тем меньше их габариты при одном и том же модуле. Уменьшение зубьев допустимо лишь до определенного предела. Если число зубьев z будет меньше минимально допустимого zmin, то при изготовлении путем нарезания режущий инструмент срезает часть зуба, возникает подрезание зубьев у ножки (рис.3). Профиль зуба из-за подрезания искажается, нарушается плавность зацепления, уменьшается прочность зуба. Минимально допустимое число zmin зубьев при угле зацепления α = 20° и коэффициенте высоты головки ha* = 1 равно 17 (zmin = 17), а при α = 15° – zmin =30. При изготовлении зубчатых колес иногда применяют зубья укороченной высоты с коэффициентом высоты головки ha* = 0,8. Это позволяет получить без подреза меньшее число зубьев на шестернях. Так при α = 20° и ha* = 0,8 минимально допустимое число зубьев zmin = 14. Отношение угловых скоростей ведущего и ведомого колес называют передаточным отношением i, а отношение числа зубьев колеса к числу зубьев шестерни – передаточным числом u. Для редукторов (замедляющих передач) абсолютные значения i и u совпадают. Передаточное число относится только к паре зубчатых колёс, оно всегда положительное, больше единицы и является частным случаем передаточного отношения. Число зубьев колес обозначают буквой z с индексом, соответствующим индексу колеса. Основной характеристикой размеров зубьев является модуль m – отношение окружного шага к числу π. Модули стандартизированы и имеют размерность в миллиметрах. Зубчатые колеса (передачи) с модулем m < 1 называют мелкомодульными. 1.4 Применение зубчатых передач в приборостроении Зубчатые передачи в приборостроении обычно используют не как силовые для передачи значительных моментов сил, а как кинематические для получения требуемых скоростей вращения. Зубчатую передачу в этом случае не рассчитывают на прочность, модуль выбирают из стандартного ряда по конструктивным соображениям. Применение малых модулей позволяет уменьшить габариты колес и увеличить плавность передачи при сохранении габаритов за счет увеличения числа зубьев. При заданном диаметре стоимость колес с уменьшением модуля возрастает, но повышается точность работы зубчатой пары, КПД таких передач 0,94 ... 0,98. 2. Фрикционные передачи. Назначение. Достоинства, недостатки. Особенности конструкций. Применение в устройствах перемещения носителей информации (бумаги, магнитных лент, карт). Фрикционная передача - механизм, служащий для передачи вращательного движения от одного вала к другому с помощью сил трения, возникающих между насаженными на валы и прижатыми друг к другу дисками, цилиндрами или конусами. Силы прижатия создаются пружинами, поджимными винтами, силами тяжести и т.д. Фрикционная передача (от лат. frictio, родительный падеж frictionis — трение) - механическая передача, в которой движение передаётся или преобразовывается с помощью сил трения между телами качения — цилиндрами, конусами и т.д., прижимаемыми друг к другу. Назначением их является изменение скорости вращательного движения (рис.2.1 а), или преобразование вращательного движения в поступательное (рис.2.1 в). Рис. 2.1 Рассматривают следующие виды фрикционных механизмов в зависимости от расположения осей и валов: – с параллельными (рис.2.1 а,в) – с пересекающимися (рис.2.1 г) осями; – с нерегулируемым, постоянным (рис. 2.1 а, г) – с регулируемым, плавно измеряемым передаточным отношением (i=var) (рис.2.1 б). Применяют фрикционные механизмы в приводах лентопротяжных, бумагопротяжных устройств, прессах, устройствах транспортирования. Достоинства данного вида механизмов это простота конструкции, изготовления, бесшумность в работе, автоматическое предохранение от перегрузок (за счет проскальзывания звеньев), отсутствие мертвого хода, возможность плавного бесступенчатого изменения передаточного отношения. К недостаткам отнесем непостоянство заданного передаточного отношения (за счет отсутствия жесткой кинематической связи между ведущим и ведомым звеньями), необходимость наличия нажимных устройств для прижатия тел качения друг к другу, усиленный износ в местах прикосновения (за счет больших удельных давлений), сравнительно низкий КПД (0,7—0,9), большие нагрузки на валы и опоры (как следствие необходимость увеличения размеров), нагрев при работе. В связи с указанными недостатками фрикционные передачи не получили такого широкого распространения как зубчатые. Эти передачи используют преимущественно в приборах (спидометры, магнитофоны, принтеры, нумераторы и др.) Всякое движение соприкасающихся звеньев (диски, цилиндрические или конические катки, цилиндры, конуса) фрикционных механизмов сопровождается их относительным скольжением. Рассмотрим виды скольжения (упругое и геометрическое), а также буксование. Упругое скольжение представляет собой скольжение, возникающее из-за различной упругой деформации ведущего и ведомого звеньев в зоне контакта. Напряжения в этой зоне различаются по величине и по знаку. Поверхностные слои ведущего катка 1 (рис. 2.1, а), нагруженного движущим (вращающим) моментом Мд по мере приближения к площадке ВА контакта сжимаются, а проходя ее – растягиваются. На ведомое звено действует момент сопротивления М2, направленный в сторону, противоположную направлению момента Мд. В точке А волокна ведущего катка растянуты, а ведомого – сжаты. Под действием сил трения в точке В площадки контакта волокна, ведущего катка сжаты, а ведомого – растянуты. В пределах площадки контакта волокна каждого катка меняют свою деформацию, скользя друг по другу. Скорость упругого скольжения составляет как правило 0,2—0,3% от величины окружной скорости катков, и имеет свойство увеличиваться с увеличением площадки контакта, т.е. с уменьшением модуля упругости материала, следовательно КПД фрикционных передач тем меньше, чем меньше модуль упругости материала катков. Геометрическое скольжение представляет собой скольжение за счет разности величин скорости точек касания звеньев фрикционного механизма вдоль линии контакта. Различают следующие виды скольжения разнотипных передач: – между двумя катками конусной формы (рис. 2.1 г) с несовпадающими вершинами конусов. Чистое качение может быть по линии касания окружностей диаметров d1 и d2. Чистое качение может быть по линии касания окружностей диаметров В остальных точках, лежащих по линии АВ контакта катков, наблюдается проскальзывание. – если катки имеют цилиндрическую форму и вращаются около параллельных осей, а также когда вершины образующих конусов катков совпадают (рис. 2.1 г) геометрическое скольжение отсутствует. Буксование – это проскальзывание, вызванное нагрузкой передачи, возникающее когда движущая сила больше величины силы сцепления между звеньями, и ведущее к местному интенсивному износу поверхности ведомого звена, что нежелательно. Как правило, буксование является одной из причин использовать для ведомых звеньев более износостойкий материал, чем материал ведущих звеньев, т.к. местный износ ведомого звена в этом случае заменит равномерный износ всей поверхности ведущего звена. Материалы катков фрикционных механизмов должны иметь высокую контактную прочность и износостойкость для обеспечения необходимой долговечности, значительный коэффициент трения для уменьшения силы нажатия колес, высокий модуль упругости для обеспечения минимального проскальзывания, высокую коррозионную стойкость и теплопроводность, т.е. это легированные стали ШХ15, 18ХН3А, закаленные до HRCэ 56 … 62. Обычно катки фрикционных передач выполняют из разных материалов, образующих пары с повышенным трением: сталь-сталь, сталь-текстолит, сталь-резина, сталь-асбест и др. Существуют рекомендации по изготовлению ведущего катка из более мягкого материала, что обеспечивает высокий коэффициент трения, меньшую силу прижатия и снижение шума, но при этом получают меньший КПД и большее упругое скольжение. Фрикционные передачи применяются в устройствах перемещения следующих устройств для перемещения носителей информации (бумаги, магнитных лент, карт): Перьевые плоттеры. Существует два типа ПП: планшетные, в которых бумага неподвижна, а перо перемещается по всей плоскости изображения, и барабанные (или рулонные), в которых перо перемещается вдоль одной оси координат, а бумага – вдоль другой, за счет захвата транспортным валом, обычно фрикционным. Перемещения выполняются при помощи шаговых или линейных электродвигателей, создающих довольно большой шум. Нумератор – еще один вид специфического оборудования, предназначенный для нанесения на различные бумаги неповторяющихся чисел и знаков. Область применения нумераторов – нумерация билетов, чеков, счетов, акций и других ценных бумаг или бланков строгой отчетности. Различаются нумераторы по разрядности печатающей головки, способу подачи бумаги и возможности подключения дополнительного оборудования. Настольная нумерационная машина с фрикционной подачей отличается простотой конструкции и высокой надежностью. Две 7-ми разрядные нумерационные головки имеют раздельный электромагнитный привод и раздельное программирование позиций печати. Задача Вариант №36 Для вращения вала перистальтического насоса рассчитать одноступенчатый зубчатый механизм с цилиндрическими зубчатыми колесами. Задано: Твых = 0,6 Н·м; nвых = 335 мин-1; i = 3,82 Определить: d1, da1, df1, h, d2, da2, df2, a, b1, b2, Твд, Pдв, Tдв, Ft, Ƞ Рассчитываемый механизм служит для уменьшения скорости вращения электродвигателя в i число раз и состоит из пары находящихся в зацеплении цилиндрических зубчатых колес (шестерни и колеса). Зубчатые колеса устанавливаются на валах, которые поддерживаются в требуемом положении опорами. Каждый вал имеет две опоры (скольжения или качения), закрепленные в корпусе. Быстроходный вал редуктора соединен с валом электродвигателя муфтой. В качестве опор принимаем подшипники качения. Ориентировочно определяем требуемую мощность Pдв электродвигателя, приняв предварительно значения КПД: - КПД зубчатой передачи Ƞз = 0,9 - КПД подшипника качения Ƞп = 0,99 - КПД муфты Ƞм = 0,97 Тогда Pдв = k·Pвых /Ƞ, Вт (1) Где k – коэффициент запаса, учитывающий необходимость преодоления динамических нагрузок в момент разгона, принимаемый равным 1,05 …1,1.; Pвых = Tвых·ωвых – требуемая мощность на выходном валу; ωвых = 2π· nвых/60 – угловая скорость выходного вала, рад/с; nвых – угловая скорость выходного вала в об/мин; Tвых – момент на выходном валу, Н·м; Ƞ - коэффициент полезного действия электромеханического привода, для выбранной схемы он равен Ƞ = Ƞм· Ƞп4· Ƞз = 0,97·0,994·0,9 = 0,8386 (2) Скорость вращения выходного вала в рад/с равна ωвых = (2·3,14·335)/60 = 35,03 рад/с (3) Подставив значения Ƞ, Tвых, ωвых в выражение (1) и приняв k = 1,1, получим Pдв = (k·Tвых·ωвых)/ Ƞ = (1,1·0,6·35,03)/0,8386 = 27,56 Вт. Частота вращения электродвигателя nдв = nвых·i = 335·3,82 = 1279,7 об/мин (4) Из серии двигателей, имеющих скорости вращения 1250, 1280, 1300 об/мин выбираем электродвигатель с n = 1280 об/мин и мощностью P≥17,3 Вт. Выбираем число зубьев z2 шестерни. Так как zmin = 17, а рекомендуемое значение числа зубьев шестерни 17 – 30, принимаем z1 = 21. Число зубьев зубчатого колеса z2 определяем по формуле z2 = z1·i = 21·3,82= 80,22. (5) Так как колесо должно содержать целое число зубьев, принимаем z2 =80. Тогда фактическое передаточное отношение зубчатой передачи iф = z2/z1 = 82/20 = 3,8 (6) Относительная погрешность зубчатой передачи ∆i % = | i−iф 𝑖 |·100% = | 3,82−3,8 3,82 |·100% = 0,05 (7) Допустимая погрешность ∆i передаточного отношения не должна превышать 3,5%. Диаметр ведущего вала, то есть вала шестерни, принимают близким по размеру диаметру вала двигателя. Считаем, что dв ≥ 3 мм. Выбираем значение модуля m из стандартного ряда модулей (0,15; 0,2; 0,25; 0,3; 0,4; 0,5; 0,6; 0,8; 1; 1,25… мм). Применение малых модулей позволяет уменьшить габариты колес или при сохранении габаритов увеличить плавность передачи за счет увеличения числа зубьев. Принимаем m = 0,5, чтобы выполнялось условие, при котором диаметр окружности впадин зубьев df шестерни был бы больше диаметра ее ступицы, т.е. df1 > 2dв. Предполагая прямозубый тип зубчатых колес, определим диаметр делительной окружности колеса (ведомого вала): d2 = m·z2 = 0,5·82 = 41 мм. (8) Линейная скорость зубчатого колеса в зацеплении v = ωвых· d2/2 = (35,03·41)/ (2·10-3) = 0,71 м/с (9) При линейных скоростях v < 6 м/с принимают тип передачи – прямозубая. У зубчатых колес со стандартной (нормальной) высотой зуба коэффициент высоты головки зуба ha* = 1, ак коэффициент радиального зазора с* зубьев в зацеплении зависит от модуля и равен с* = 0,5 при m ≤ 0,5 мм с* = 0,35 при 0,5 < m < 1 мм с* = 0,25 при m ≥ 1,0 мм Высота головки зубьев колес ha = ha*·m = 1·0,5 = 0,5 мм. (10) Высота ножки зубьев колес hf = m(ha*+ с*) = 0,5 (1+0,5) = 0,75 мм. (11) Диаметры делительных окружностей зубчатых колес шестерни d1 = m·z1 = 05·2 = 10 мм, (12) колеса d2 = m·z2 = 0,5·82 = 41 мм. (13) Диаметры окружностей вершин зубьев колес: шестерни da1 = d1 + 2ha = 100 + 2·0,5 = 11 мм, (14) колеса da2 = d2 + 2ha = 41 + 2·0,5 = 41,15 мм. (15) Диаметры окружностей впадин зубьев колес: шестерни df1 = d1 – 2hf = 10 - 2·0,75 = 8,5 мм, (16) колеса df2 = d2 – 2hf = 41 - 2·0,75 = 39,5 мм. (17) Межосевое расстояние а зубчатой передачи: а = (d1+ d2)/2 = (10 + 41)/2 = 30.5 мм. (18) Длина зуба b определяется по формуле d = ψbd·d, (19) где ψbd – коэффициент ширины b венца колеса по диаметру d делительной окружности, рекомендуется принимать ψbd = 0,005…. 0,3. Длина зуба колеса равна b2 = 0,05·72.5 = 3,625 мм ≈3,63 мм. (20) Принимаем b2 = 3мм. Длина зуба шестерни, как более нагруженного звена, определяется по формуле b1 = b2 + (0,5…1мм) = 3+0,5 = 3,5 мм. (21) Окружное усилие в зацеплении определяется по формуле ft = 2Tвых/d2 = (2·0,6·103)/41 = 29,2 Н. (22) Уточняем значение КПД зубчатой пары 1 1 1 1 1 1 Ƞзз = 1- [𝜋 · с · 𝑓 · Ԑy ( + )] · = 1- [3,14 · 1,09 · 0,1 · 1,5 ( + )] · = 𝑧1 𝑧2 2 20 82 2 = 0,98, (23) где f = 0,1 – коэффициент трения по стали (шестерня и зубчатое колесо стальные); Ԑy = 1,5 – коэффициент перекрытия пары прямозубых колес; с – коэффициент, учитывающий уменьшение КПД зубчатого зацепления при малых нагрузках, Ft с= 𝐹+2,92 𝐹𝑡+0,174 = 29,2+2,92 29,2+0,174 = 21,82 19,074 = 1,09. (24) Вращающий момент на ведущем валу зубчатого механизма: Tвд = Tвых / (iф· Ƞзз · Ƞп4) = 0,6 (3,8· 0,98 · 0,994) = 2,14 Н· м. (25) Вращающий момент на валу электродвигателя Tдв = Твд / Ƞm = 2,14 / 0,97 = 2,2 Н· м. (26) Кинематическая схема механизма приведена на рисунке. 1- Электродвигатель; 2- муфта; 3- опора качения; 4- шестерня (ведущее зубчатое колесо); 5- ведомое зубчатое колесо; 6 – корпус; I- вал электродвигателя; II- ведущий вал; III – выходной вал. Список используемой литературы 1. Сурин В.М. Техническая механика. Учеб.пособие. - Мн.: БГУИР, 2004. – 292с. 2. Красковский Е.Я., Дружинин Ю.В., Филатов Е.М. Расчет и конструирование механизмов приборов и вычислительных систем.- М.: Высш. шк., 1991. – 431с. 3. Ванторин В.Д. Механизмы приборных и вычислительных систем.- М.: Высш. шк., 1985. – 415с. 4. Вопилкин Е.А. Расчет и конструирование механизмов приборов и систем. – М.: Высш. шк., 1980. – 463с. 5. Прикладная механика. / Под общ.ред. А.Т.Скойбеды – Мн.: Выш. шк., 1997 – 522с. 6. Детали машин: курс лекций / И.Е. Говорова. - Волгоград : ГБОУ СПО ВПТКР, 2014. - 147с.