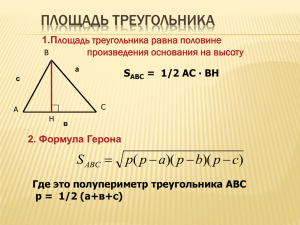
Технологическая карта урока по теме: «Площадь параллелограмма» Предмет - Геометрия. Класс 8 Базовый учебник – Л.С. Атанасян, В.Ф.Бутусов, С.Б. Кадомцев и др. «Геометрия 7-9» Тема урока – Площадь параллелограмма Цель урока – Вывести формулу площади параллелограмма и научить применять её для решения геометрических задач. Задачи урока: обучающие: создать условия учащимся для формирования представлений об измерении площади параллелограмма; для формирования умений выводить формулу для вычисления площади параллелограмма на основе основных свойств площадей многоугольников, применять её при решении задач различного уровня сложности. развивающие: способствовать формированию интеллектуальных умений и владения мыслительными операциями: анализом, синтезом, доказательством, обобщением. воспитательные: развивать познавательный интерес, способствовать пониманию необходимости интеллектуальных усилий для успешного обучения, положительного эффекта настойчивости для достижения цели. Тип урока - Урок усвоения новых знаний Необходимое оборудование: презентация PowerPoint по теме урока, мультимедийная аппаратура, раздаточный материал. Планируемый результат: Предметные умения УДД Уметь выводить формулу для вычисления площади Личностные: осознание математической составляющей параллелограмма. окружающего мира. Уметь устанавливать логические отношения между Регулятивные: осознание возникшей проблемы, данными и искомыми. определение последовательности и составление плана и последовательности действий для решения возникшей Использовать для решения геометрических задач проблемы, внесение необходимых дополнений и графические модели в соответствии с содержанием коррективов в план и способ действия в случае задания. расхождения эталона, реального действия и его результата с учётом оценки этого результата самим обучающимся, учителем, товарищами; Познавательные: постановка и формулирование проблемы, самостоятельное создание алгоритмов деятельности при решении проблем творческого и поискового характера, выбор наиболее эффективных способов решения задач в зависимости от конкретных условий, рефлексия способов и условий действия, контроль и оценка процесса и результатов деятельности. Коммуникативные: умение с достаточной полнотой и точностью выражать свои мысли в соответствии с задачами и условиями коммуникации; владение монологической и диалогической формами речи, умение работать индивидуально и в парах. № Этап урока 1 Организационный момент 2. Проверка домашнего задания СТРУКТУРА И ХОД УРОКА Деятельность учителя Деятельность ученика Приветствует. Проверяет готовность учащихся. Организует внимание. Подготовка класса к работе. Включение в деловой ритм. 1.Отвечают на вопросы учителя к 1.Организует теоретический опрос заданию. учащихся по слайду: Задание: Перед нами две фигуры, составленные из одних и тех же геометрических фигур. Части, на которые разрезана одна фигура, позволили получить другую фигуру. 1. 2. 3. 4. 5. (1) (2) Равны ли площади этих фигур? Почему? Какими основными свойствами площадей можно воспользоваться для объяснения равенства площадей фигур? Можно ли назвать эти фигуры равными? Почему? Площадь, какой из двух фигур вы можете вычислить? Как? Площади, каких многоугольников вы научились вычислять? Какие формулы вы при этом используйте? Формируемые УУД Личностные: самоопределение; Регулятивные: целеполагание; Коммуникативные: планирование сотрудничества с учителем и сверстниками. Регулятивные: контроль, коррекция и оценка процесса и результатов деятельности. Коммуникативные: выражение и аргументация своих мыслей 6. Могли бы вы вычислить площадь первой фигуры, если бы не было второй фигуры? 7. Что нужно знать для вычисления площади первой фигуры в этой ситуации? 2. Устанавливает правильность выполнения домашнего задания, выявляет и способствует устранению возникших проблем. 1) Докажите теорему о площади прямоугольника. (1 учащийся заранее готовит доказательство на доске) 2) Прокомментируйте решение домашней задачи №456: Сколько потребуется кафельных плиток квадратной формы со стороной 15 см, чтобы облицевать ими стену, имеющую форму прямоугольника со сторонами 3м и 2,7м? 2. Осуществляют самопроверку решения №456, объясняют каждый шаг решения. Слушают и оценивают ответы товарищей. 3. Актуализация знаний 1. Предлагает устно выполнить решение задач по готовым чертежам. (Слайд). 2.Обеспечивает актуализацию субъективного опыта в процессе поиска решения. 1.Устанавливают логические Познавательные: анализ задачи отношения между данными и с целью выявления искомыми величинами. существующих связей между данными и искомыми 2.Выбирают способ решения задачи. величинами, выбор эффективного способа решения. Регулятивные: контроль и коррекция процесса и результатов деятельности. 3. Формулирует условие к задаче №3 (создаёт проблемную ситуацию): Площадь прямоугольного участка земли АВСД =20 м2. Требуется сравнить её с площадью участка, имеющего форму параллелограмма МВСК. Что вы можете сказать? Может ли такая ситуация встретиться в жизни? 4. Постановка цели и задач урока. Мотивация учебной деятельности учащихся. Коммуникативные: умение с достаточной полнотой и точностью выражать свои мысли, опираясь на 3.Находят способ решения задачи или определения и теоремы. выдвигают версии при ответе на вопрос, т.к. неизвестно по какой формуле находится площадь. 4. Предлагает сформулировать возникшую проблему. 4.Формулируют проблему: как найти площадь параллелограмма? Предлагает учащимся сформулировать тему и цели урока в связи с возникшими затруднениями в решении задачи №3. Определяют тему и цели урока. Записывают тему урока в тетрадь. Познавательные: самостоятельное выделение и формулирование познавательной цели. Личностные: самоопределение. Регулятивные: целеполагание. Коммуникативные: выражение и аргументация своих мыслей. 5. Первичное усвоение новых знаний 1.Организует учащихся по исследованию проблемной ситуации по предварительно выполненному в тетради и на доске чертежу параллелограмма: делит класс на группы по 2-4 учащихся и даёт задание: 1.Учащиеся обсуждают решение Познавательные: задачи в группах, затем озвучивают моделирование, самостоятельное создание варианты решения. алгоритмов деятельности, анализ, синтез, построение логической цепи рассуждения, доказательство. Дано: АВСД-параллелограмм, АД=а, ВН-высота, ВН=h Найти: SАВСД При формулировке задания вводит понятие основания и высоты параллелограмма. 2. В случае затруднений учащихся направляет их деятельность с помощью наводящих вопросов: - Площадь какой фигуры мы умеем находить? - Можно ли выполнить преобразование параллелограмма (дополнительное построение), чтобы получить фигуры, площади которых мы умеем находить? - Почему площадь параллелограмма равна площади прямоугольника? -Какой можно сделать вывод? -Какие измерения нужно выполнить, чтобы найти площадь параллелограмма? 3.Предлагает решить задачу: Измерьте высоту и основание параллелограмма (на чертеже) и подсчитайте площадь. 4.Предлагает оформить решение задачи в виде теоремы на доске и в тетрадях. 2.В случае затруднения отвечают на вопросы учителя, в процессе рассуждений указывают на дополнительные построения на чертеже параллелограмма. С А В К D М 3.Записывают решение задачи в тетради, один из учащихся производит измерения и вычисления на доске. 4.Формулируют теорему. Записывают формулировку и доказательство теоремы в тетрадь, один учащийся выполняет запись на доске. Коммуникативные: сотрудничество в поиске и выборе способа решения возникшей проблемы. Регулятивные: планирование, прогнозирование. 6 Первичная проверка понимания изученного 1. Устанавливает осознанность восприятия учебного материала. Предлагает решить типовые задачи из учебника. №459: а) Пусть а-основание, h- высота, а Sплощадь параллелограмма. Найдите S, если а=15 см, h=12 см; б) а, если S=34см2, h=8,5 см; г) а, если S=162 см2, h=1/2 а. №468(в): ) Пусть а- основание, h- высота, а Sплощадь параллелограмма. Найдите h, если S=37,8 см2. №464(в) Пусть а и b - смежные стороны параллелограмма, S-площадь, а h1 и h2 – высоты. Найдите h1 и h2. если S=54см2, а=4,5 см, b=6см. 2. По результатам задачи № 464(в) предлагает ответить на вопрос: Что вы можете сказать о длинах высот, проведенных к большей и меньшей стороне параллелограмма? 3. Проводит коррекцию пробелов в осмыслении материала и в записи решения. 1.Выполняют решение задач, самостоятельно оформляют, создают чертёж, комментируя с мест; корректируют ответ товарища. Познавательные: структурирование знаний, выбор способа решения задач. №459(а)-устно, Регулятивные: контроль, оценка, коррекция. №459(б,в), №468(в), №464(в)письменно, комментируя с мест, с пошаговой проверкой записи по эталону. (Слайды). Коммуникативные: выражение и аргументация своих мыслей, согласия или несогласия с мнением отвечающего. При решении задач №459(б,в), №468(в) выводят формулы для вычисления величин а и h. 2.Отвечая на вопрос учителя, делают вывод: К большей стороне параллелограмма проводится меньшая высота и наоборот. 7. Первичное закрепление Обеспечивает повышение уровня осмысления изученного материала, глубины понимания: 1. Предлагает 3 варианта задачсамостоятельную работу обучающего характера с последующей проверкой и коррекцией: 1 вариант: Стороны параллелограмма 10 см и 6 см, а угол между этими сторонами 150°. Найдите площадь параллелограмма. 2 вариант: Острый угол параллелограмма равен 30°, а высоты проведенные из вершины тупого угла, равны 4 см и 3 см. Найдите площадь параллелограмма. 3 вариант: Найдите площадь ромба, диагонали которого равны 8 см и 6 см. 2. Подводит учащихся к выводу, что площадь ромба равна половине произведения его диагоналей. 1.Самостоятельно выполняют решение задачи с выполнением чертежей по вариантам, затем проверяют его. (Слайды). Личностные: самоопределение. Познавательные: анализ объектов с целью составления алгоритма решения задачи. 2.Корректируют свои решения с учётом возникших затруднений или Регулятивные: контроль, ошибок; записывают решение, если коррекция. оно не было найдено. 3.Записывают в тетрадь формулу для вычисления площади ромба. 8. Постановка домашнего задания Даёт комментарий к домашнему заданию: 1 уровень – обязательный; 2-3 уровень - для желающих, на дополнительную оценку. 9. Подведение итогов Рефлексия Даёт качественную оценку работы класса и количественную оценку отдельных учащихся (активность +правильность +умение обосновывать ответ). Организует рефлексию с помощью карточек самооценивания: Оцените: свою работу на уроке с помощью фраз: -Сегодня на уроке я узнал (узнала)… - Сегодня на уроке я научился (научилась) …. - Я пока еще не умею …. - Я стал (стала) лучше…. - Где в жизни я смогу применить полученные знания… Получают и записывают задание: 1 уровень § 2, вопрос 4, с.133; №459(г), №460, №464(б) 2 уровень: Найдите углы параллелограмма. Если его площадь равна 20 см2, а высота, проведенная из вершины тупого угла, делит одну из сторон на отрезки 2 см и 8 см, считая от вершины острого угла. 3 уровень: Сравните площади параллелограмма и прямоугольника, если они имеют одинаковые основания и одинаковые периметры. Осуществляют самооценку собственной учебной деятельности, соотносят цели и результаты, степень их соответствия. Сдают карточки самооценивания. Личностные: смыслообразование. Регулятивные: оценкаосознание уровня и качества усвоения; контроль.