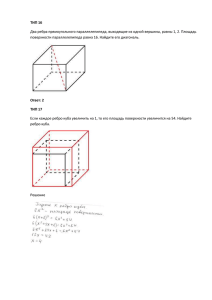
СБОРНИК КОНТРОЛЬНЫХ РАБОР ПО ГЕОМЕТРИИ 11 класс Пояснительная записка Контрольные работы содержат задания на воспроизведение (40%), применение (40%) и интеграцию (20%) предметных знаний. Тематические контрольные работы включают критерии оценивания, позволяющие отследить уровень усвоения учащимися стандартов данной темы. Содержательная матрица дает возможность учителю провести качественный анализ контрольной работы и спланировать коррекционную работу индивидуально для каждого ученика. Предложение содержательной матрицы и критериев оценивания дает возможность учащимся планировать свою учебную деятельность для достижения более качественных результатов и впоследствии ее коррекцию. . Контрольная работа №1 11 класс. Тема: «Призма. Боковая и полная поверхность призмы». Цель: проверить уровень усвоения ГОСО: - знание элементов призмы; - умение находить элементы призмы; - формулы площади боковой и полной поверхностей призмы; - умения решать задачи на применение теоретических знаний по теме. I вариант. 1.Стороны основания прямого параллелепипеда равны 3 см и 5 см, угол между ними равен 600. Большая диагональ параллелепипеда равна 10 см. Найти боковое ребро параллелепипеда. 2.В основании прямой треугольной призмы лежит прямоугольный треугольник с катетами 8 см и 6 см. Определите боковое ребро призмы, если площадь боковой поверхности равна 120 см2. 3. Основание прямой призмы - ромб с острым углом 300. Боковая поверхность призмы равна 96 дм2, а полная – 132 дм2. Найдите высоту призмы. 4.Диагональ боковой грани правильной треугольной призмы наклонена к плоскости основания под углом α, а площадь этой грани равна Q. Найдите площадь полной поверхности призмы. II вариант. 1.В основании прямой призмы лежит равнобедренный треугольник с основанием 5 см. Высота призмы – 3 см. Определите площадь сечения призмы плоскостью, проходящей через основание равнобедренного треугольника и противоположную вершину верхнего основания призмы, если диагонали равных боковых граней равны 6,5 см. 2.Основанием прямого параллелепипеда является ромб с диагоналями 6 см и 8 см. Диагональ боковой грани равна √61 см. Определите боковую поверхность призмы. 3. Основание прямой призмы – ромб с высотой 2 дм. Боковая поверхность призмы равна 96 дм2, а полная - 128 дм2. Найдите высоту призмы. 4.Диагональ боковой грани правильной треугольной призмы наклонена к плоскости основания под углом α, а площадь основания этой призмы S. Найдите площадь полной поверхности призмы. Распределение заданий по содержанию и уровню сложности Содержательная Воспроиз- Примене- Интеграция Процентное линия ведение ние знаний соотношение знаний знаний в тексте Нахождение элементов призмы №1, 25 % Площадь боковой поверхности №2 25% призмы Площадь боковой и полной №3 25% поверхности прямой призмы. Площадь боковой и полной №4 25% поверхности призмы (буквенные значения) Процентное соотношение заданий 25% 50% 25% 100 % Спецификация заданий и критерии оценивания № Характеристика Проверяемые элементы зада задания ния 1 2 Нахождение элементов призмы. Площадь боковой поверхности призмы. Построение чертежа по условию задачи. Знание элементов призмы. Установление связи между данными в задаче. Оформление решения задания. Построение чертежа по условию задачи. Применение теоремы Пифагора. Знание формулы боковой поверхности призмы. Балл за выполнение проверяемого элемента 1 балл Балл за выполнение задания 5 баллов 1 балл 2 балла 1 балл 1 балл 5 баллов 1 балл 1 балл 3 4 Площадь боковой и полной поверхности прямой призмы. Площадь боковой и полной поверхности призмы (буквенные значения). Умение применять формулу при решении задачи. Оформление решения задания. Установление связи между данными в задаче. Формула вычисления площади боковой поверхности. Формула вычисление площади ромба. Формула вычисления полной поверхности призмы. Умение применять формулы при решении задачи. Соотношения в прямоугольном треугольнике. Формула вычисления площади полной поверхности призмы. Умения работать с буквенными выражениями. 1 балл 1 балл 1 балл 1 балл 5 баллов 1 балл 1 балл 1 балл 2 балла 1 балл 5 баллов 2 балла Критерии оценивания: 1-9 баллов – «2» 10-13 баллов – «3» 14-18 баллов – «4» 19-20 баллов – «5» Контрольная работа №2 11 класс. Тема: «Пирамида. Боковая и полная поверхность пирамиды». Цель: проверить уровень усвоения ГОСО: - знание элементов пирамиды, усеченной пирамиды; - умение находить элементы пирамиды; - знание формул площади боковой и полной поверхностей пирамиды, усеченной пирамиды; - умения решать задачи на применение теоретических знаний по теме. I вариант. 1.Высота правильной четырёхугольной пирамиды равна 7 см, а сторона основания равна 8 см. Определите боковое ребро и апофему пирамиды. 2. Сторона основания правильной четырёхугольной пирамиды равна а. Двугранные углы при основании равны α. Определите площадь полной поверхности пирамиды. 3. В правильной четырёхугольной усечённой пирамиде высота равна 2 см, а стороны оснований 3 и 5 см. Найдите полную поверхность пирамиды. 4. В правильной треугольной пирамиде боковая поверхность равна 27 см2, а периметр основания – 18 см. Найдите апофему и плоский угол при вершине пирамиды. II вариант. 1.Основание пирамиды – прямоугольник со сторонами 6 см и 8 см. Каждое боковое ребро пирамиды равно 13 см. Вычислите высоту пирамиды. 2. Сторона основания правильной четырёхугольной пирамиды равна а, высота – b. Определите площадь полной поверхности пирамиды. 3. В правильной усечённой четырёхугольной пирамиде стороны оснований 8 и 2 м. Высота равна 4 м. Найдите полную поверхность пирамиды. 4. В правильной треугольной пирамиде полная поверхность равна 16√3 см2, а площадь основания - 4√3 см2. Найдите апофему и плоский угол при вершине пирамиды. Распределение заданий по содержанию и уровню сложности Содержательная Воспроиз- Примене- Интеграция Процентное линия ведение ние знаний соотношение знаний знаний в тексте Нахождение элементов пирамиды №1, 25 % Площадь полной поверхности №2 25% пирамиды Площадь полной поверхности №3 25% усечённой пирамиды Площадь боковой и полной поверхности пирамиды Процентное соотношение заданий 25% 50% Спецификация заданий и критерии оценивания № Характеристика Проверяемые элементы зада задания ния 1 2 3 4 Нахождение элементов пирамиды. Площадь полной поверхности пирамиды. Площадь полной поверхности усечённой пирамиды. Площадь боковой и полной поверхности пирамиды. Критерии оценивания: 1-9 баллов – «2» 10-13 баллов – «3» 14-18 баллов – «4» 19-20 баллов – «5» Построение чертежа по условию задачи. Знание элементов пирамиды. Установление связи между данными в задаче. Оформление решения задания. Построение чертежа по условию задачи. Соотношения в прямоугольном треугольнике. Знание формулы полной поверхности пирамиды. Умение применять формулу при решении задачи. Умение решать задачи в буквенном виде. Умение строить усечённую пирамиду. Знание формулы площади боковой поверхности усеченной пирамиды Знание формулы площади полной поверхности усеченной пирамиды Умение применять формулы при решении задачи. Установление связи между данными в задаче. Знание формулы площади боковой поверхности пирамиды. Знание формулы площади полной поверхности пирамиды. Умение применять формулы при решении задачи. №4 25 % 25% 100 % Балл за выполнение проверяемого элемента 1 балл Балл за выполнение задания 5 баллов 1 балл 2 балла 1 балл 1 балл 5 баллов 1 балл 1 балл 1 балл 1 балл 1 балл 1 балл 5 баллов 1 балл 2 балла 1 балл 1 балл 1 балл 2 балла 5 баллов Контрольная работа №3 Тема: «Объёмы многогранников». 11 класс. Цель: проверить уровень усвоения ГОСО по теме - знание формул для вычисления объёмов призмы, пирамиды, усечённой пирамиды; - умение находить объёмы многогранников; - умение установить связь между данными в задаче - умения выполнять чертежи по условию задачи; I вариант. 1.Основание прямой призмы - прямоугольный треугольник с катетами 3см и 4 см. Диагональ боковой грани, содержащей гипотенузу треугольника, равна 13 см. Найдите объём призмы. 2.Найдите объём пирамиды, в основании которой лежит параллелограмм со сторонами 2см и √3 см и углом между ними 300, если высота пирамиды равна меньшей диагонали основания. 3.Вычислите объём правильной четырёхугольной усеченной пирамиды со сторонами оснований а>b, боковое ребро которой наклонено к плоскости большего основания под углом α. 4. Основание пирамиды – равнобедренный треугольник с боковой стороной b и углом при основании β. Все двугранные углы при основании равны α. Найдите объём пирамиды. II вариант. 1.Основание прямой призмы – равнобедренный треугольник, в котором боковая сторона равна 5 см, а высота, проведённая к основанию, - 4 см. Диагональ боковой грани, содержащей основание треугольника, равна 10 см. Найдите объём призмы. 2.Найдите объём пирамиды, в основании которой лежит параллелограмм с диагоналями 4 см и 2√3 см, если угол между ними равен 300, а высота пирамиды равна меньшей стороне основания. 3.Вычислите объём правильной треугольной усечённой пирамиды со сторонами оснований а>b, боковое ребро которой наклонено к плоскости большего основания под углом α. 4.Основание пирамиды – равнобедренный треугольник с боковой стороной b и углом при вершине β. Все боковые ребра пирамиды наклонены к плоскости основания под углом α. Найдите объём пирамиды. Распределение заданий по содержанию и уровню сложности Содержательная Воспроиз- Примене- Интеграция Процентное линия ведение ние знаний соотношение знаний знаний в тексте Вычисление объёма призмы №1, 25 % Нахождение объёма пирамиды №2 25% Нахождение объёма усечённой №3 25% пирамиды. Нахождение объёма пирамиды №4 25% (условие в буквенном виде). Процентное соотношение заданий 25 % 50 % 25 % 100 % Спецификация заданий и критерии оценивания № Характеристика Проверяемые элементы зада задания ния 1 2 3 Вычисление объёма призмы. Нахождение объёма пирамиды. Нахождение объёма усечённой пирамиды. Построение чертежа по условию задачи. Знание формулы вычисления объёма призмы. Установление связи между данными в задаче. Оформление решения задания. Построение чертежа по условию задачи. Знание формулы вычисления объёма пирамиды. Умение находить площадь параллелограмма. Знание формулы теоремы косинусов. Умение применять формулы при решении задачи. Умение строить усечённую пирамиду. Знание формулы вычисления объёма усечённой пирамиды. Установление связи между данными в задаче. Умение применять формулы при решении задачи. Балл за выполнение проверяемого элемента 1 балл Балл за выполнение задания 5 баллов 1 балл 2 балла 1 балл 1 балл 5 баллов 1 балл 1 балл 1 балл 1 балл 1 балл 1 балл 2 балла 1 балл 5 баллов 4 Нахождение объёма пирамиды (условие в буквенном виде). Установление связи между данными в задаче. Знание формулы вычисления объёма пирамиды. Соотношения в прямоугольном треугольнике. Умение работать с буквенными выражениями. 2 балла 1 балл 5 баллов 1 балл 1 балл Критерии оценивания: 1-9 баллов – «2» 10-13 баллов – «3» 14-18 баллов – «4» 19-20 баллов – «5» Контрольная работа №4 Тема: «Цилиндр. Конус». 11 класс. Цель: проверить уровень усвоения ГОСО по темам «Цилиндр. Боковая и полная поверхность цилиндра», «Конус. Боковая и полная поверхность конуса». - элементы конуса и цилиндра; - сечения цилиндра и конуса: - формулы площади боковой и полной поверхностей цилиндра и конуса; - умения решать задачи на применение теоретических знаний по теме. I вариант. 1.В цилиндре радиуса 5 см проведено параллельное оси сечение, отстоящее от неё на расстоянии 3 см. Найдите высоту цилиндра, если площадь указанного сечения равна 64 см2. 2.Угол при вершине осевого сечения конуса с высотой 1 м равен 600. Чему равна площадь сечения конуса, проведенного через две образующие, угол между которыми равен 450 ? 3.Площадь основания конуса S, а образующие наклонены к плоскости основания под углом α. Найдите боковую и полную поверхность конуса. 4.Площадь осевого сечения цилиндра равна 40 см2. Длина окружности его основания 8π см. Найдите площадь полной поверхности цилиндра. II вариант. 1.В цилиндре с высотой 6 см проведено параллельное оси сечение, отстоящее от неё на расстояние 4 см. Найдите радиус цилиндра, если площадь указанного сечения равна 36 см2. 2.Угол при вершине осевого сечения конуса, с радиусом основания 1 м, равен 1200. Чему равна площадь сечения конуса, проведенного через две образующие, угол между которыми равен 600? 3.Радиус кругового сектора равен 3 м, а его угол 1200. Сектор свёрнут в коническую поверхность. Найдите радиус основания конуса и полную поверхность конуса. 4.В цилиндре площадь основания равна Q, а площадь осевого сечения М. Найдите площадь боковой поверхности цилиндра. Распределение заданий по содержанию и уровню сложности Содержательная Воспроиз- Примене- Интеграция Процентное линия ведение ние знаний соотношение знаний знаний в тексте Сечения в цилиндре №1, 25 % Сечения в конусе. №2 25% Площадь боковой поверхности №3 25% конуса. Площадь боковой и полной №4 25 % поверхности цилиндра. Процентное соотношение заданий 50 % 25 % 25 % 100 % Спецификация заданий и критерии оценивания № Характеристика Проверяемые элементы зада задания ния 1 Сечения в цилиндре. Построение чертежа по условию задачи. Знание элементов цилиндра. Балл за выполнение проверяемого элемента 2 балла Балл за выполнение задания 5 баллов 1 балл 2 3 4 Сечения в конусе. Площадь основания, боковой и полной поверхности конуса. Площадь боковой и полной поверхности цилиндра. Установление связи между данными в задаче. Оформление решения задания. Построение чертежа по условию задачи. Знание элементов конуса. 1 балл Соотношения в между сторонами у углами в треугольнике. Знание синуса, косинуса, тангенса табличных углов. Оформление решения задания. Формула вычисления площади основания конуса. Формула вычисление боковой поверхности конуса. Формула вычисления полной поверхности конуса. Умение применять формулы при решении задачи. Формула вычисления площади основания цилиндра. Формула вычисление боковой поверхности цилиндра. Формула вычисления полной поверхности цилиндра. Умение применять формулы при решении задач. 1 балл 1 балл 1 балл 5 баллов 1 балл 1 балл 1 балл 1 балл 1 балл 5 баллов 1 балл 2 балла 1 балл 1 балл 5 баллов 1 балл 2 балла Критерии оценивания: 1-9 баллов – «2» 10-13 баллов – «3» 14-18 баллов – «4» 19-20 баллов – «5» Контрольная работа №5 Тема: «Шар. Сфера». 11 класс. Цель: проверить уровень усвоения ГОСО: - знание элементов шара, сферы; - сечение шара (сферы), свойства сечения; - касательная плоскость к шару (сфере), свойство касательной плоскости; - вписанные в шар (сферу) и описанные около шара (сферы) многогранники; -площадь поверхности шара (сферы); - умение применять теоретические знания при решении задач. I вариант. 1.Сфера с центром в точке О касается плоскости. Точка А лежит в этой плоскости. Найти расстояние от точки А до точки касания, если расстояние от неё до центра сферы равно 25 см, а радиус сферы равен 15 см. 2.Сечение шара плоскостью имеет площадь 36π см2. Чему равен радиус шара и площадь поверхности шара, если сечение удалено от его центра на расстояние 8см ? 3.Все стороны равностороннего треугольника касаются шара, радиус шара равен 5 см, а сторона треугольника 6√3 см. Найдите расстояние от центра шара до плоскости треугольника. 4.В правильной четырёхугольной призме сторона основания равна 4 дм, высота 2 дм. Найдите радиус описанной около призмы сферы. II вариант. 1.Шар с центром в точке О касается плоскости. Точка В лежит в этой плоскости и удалена от точки касания на 20 см. Найдите радиус шара, если расстояние от точки В до центра шара равно 25 см. 2.Линия пересечения сферы с плоскостью имеет длину 18π см. Чему равно расстояние от центра сферы до этой плоскости и площадь поверхности сферы, если радиус сферы равен 15см? 3.Вершины равностороннего треугольника лежат на поверхности шара, радиусом 5 см. Найти расстояние от центра шара до плоскости треугольника, если стороны треугольника равны 6 см. 4.У правильной треугольной призмы высота равна 2 дм, радиус описанной около неё сферы тоже равен 2 дм. Найдите сторону основания призмы. Распределение заданий по содержанию и уровню сложности Содержательная Воспроиз- Примене- Интеграция Процентное линия ведение ние знаний соотношение знаний знаний в тексте Касательная плоскость к шару №1, 25 % (сфере) и её свойства. Секущая плоскость шара (сферы) и её свойства. Площадь поверхности шара (сферы) Вписанные в шар(сферу) многогранники. Процентное соотношение заданий №2, №3 25% 50% Спецификация заданий и критерии оценивания № Характеристика Проверяемые элементы зада задания ния 1 2 3 4 Касательная плоскость к шару (сфере) е её свойство. Секущая плоскость шара (сферы) и её свойства. Вписанный в шар и описанный около шара треугольник. Вписанные в сферу многогранники. Критерии оценивания: 1-9 баллов – «2» 10-13 баллов – «3» 14-18 баллов – «4» 19-20 баллов – «5» Понятие – касательная плоскость 50% №4 25% 25% 100 % Балл за выполнение проверяемого элемента 1 балл Балл за выполнение задания 5 баллов Свойство касательной плоскости. 2 балла Применение теоремы Пифагора. Оформление решения задания. Построение чертежа по условию задачи. Свойство секущей плоскости шара (сферы). Применение формул длины окружности и площади круга. Применение теоремы Пифагора Вычисление площади поверхности шара (сферы) Установление связи между данными в задаче. Радиус окружности, вписанной в равносторонний треугольник и описанной около равностороннего треугольника. Применение теоремы Пифагора. Свойство секущей плоскости. Построение чертежа по условию задачи. Понятие - правильная призма и её элементы. Установление связи между данными в задаче. Применение теоремы Пифагора. 1 балл 1 балл 1 балл 1 балл 5 баллов 1 балл 1 балл 1 балл 1 балл 2 балла 5 баллов 1 балл 1 балл 1 балл 2 балла 1 балл 1 балл 5 баллов Контрольная работа №6 Тема: «Объём тел вращения». 11 класс. Цель: проверить уровень усвоения ГОСО: - знание формул для вычисления объёма конуса, цилиндра, шара и его частей; - знание элементов тел вращения; - умение применять формулы для вычисления объёмов; - умение применять теоретические знания при решении задач. I вариант. 1. Высота цилиндра равна 5 см, а диагональ осевого сечения – 13 см. Найти объём цилиндра. 2. Прямоугольный треугольник с катетом 2√3 см и принадлежащим к нему углом 600 вращается вокруг второго катета. Найдите объём тела вращения. 3. На расстоянии 12 см от центра шара проведено сечение, радиус которого равен 9 см. Найти объём шара и площадь его поверхности. 4. Образующая конуса равна 10 см, а площадь его боковой поверхности равна - 60π. Найти объём вписанного в конус шара. II вариант. 1.Радиус цилиндра равен 4 см, а диагональ осевого сечения равна 10 см. Найти объём цилиндра. 2. Прямоугольный треугольник АВС с гипотенузой АВ, равной 6 см и углом А равным 300, вращается вокруг катета АС. Найдите объём тела вращения. 3. Через точку, лежащую на сфере, проведено сечение радиусом 3 см под углом 60 0 к радиусу сферы, проведённому в данную точку. Найдите площадь сферы и объём шара. 4. Объём конуса равен 128π, а его высота – 6. Найдите объём описанного около конуса шара. Распределение заданий по содержанию и уровню сложности Содержательная Воспроиз- Примене- Интеграция Процентное линия ведение ние знаний соотношение знаний знаний в тексте Объём цилиндра №1, 25 % Объём конуса №2 25% Объём шара, площадь сферы №3 25% Вписанные и описанные тела и их №4 25% объёмы Процентное соотношение заданий 25% 50% Спецификация заданий и критерии оценивания № Характеристика Проверяемые элементы зада задания ния 1 2 3 Объём цилиндра. Объём конуса. Объём шара, площадь поверхности шара. Элементы цилиндра. Теорема Пифагора. Формула объёма цилиндра. Оформление решения задания. Построение чертежа по условию задачи. Формула вычисления объёма конуса. Соотношения в прямоугольном треугольнике. Оформление решения задачи. Установление связи между данными в задаче. Свойство секущей плоскости. Формула вычисления объёма шара. Теорема Пифагора. Формула вычисления площади поверхности шара (сферы). 25% Балл за выполнение проверяемого элемента 1 балл 1 балл 1 балл 2 балла 1 балл 100 % Балл за выполнение задания 5 баллов 5 баллов 1 балл 1 балл 2 балла 1 балл 1 балл 1 балл 1 балл 1 балл 5 баллов 4 Вписанный (описанный) в шар конус. Критерии оценивания: 1-9 баллов – «2» 10-13 баллов – «3» 14-18 баллов – «4» 19-20 баллов – «5» Построение чертежа по условию задачи. Формула объёма конуса. Формула объёма шара. Установление связи между данными задачи. 1 балл 1 балл 1 балл 2 балла 5 баллов