Волновой алгоритм для поиска пути между двумя
ячейками – источником и приемником
дискретного рабочего поля (ДРП).
•
ДРП – это прямоугольник, разбитый на квадратные ячейки одинакового
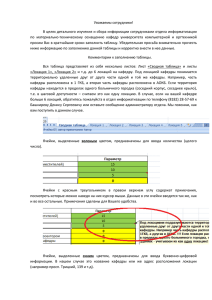
размера. Ячейки ДРП подразделяются на свободные, препятствия,
источники и приемники. На рисунке свободные ячейки имеют светлозеленый цвет, а препятствия – светло-коричневый. Источник залит синим
цветом, а приемник – черным.
Путь может быть проложен только по свободным ячейкам
.
Описание волнового алгоритма
• Рассматривается алгоритм построения ортогонального пути.
Алгоритм состоит из двух частей.
• В первой от источника к приемнику распространяется волна.
Волна, идущая от источника к приемнику, на каждом шаге
первой части алгоритма пополняется свободными ячейками,
которые, во-первых, еще не принадлежат волне, и, во-вторых,
являются 4-соседями ячеек, попавших в волну на предыдущем
шаге.
• Во второй выполняется обратный ход, в
процессе которого из ячеек волны
формируется путь.
Волновой алгоритм либо находит
кратчайший путь от источника к приемнику,
либо информирует о неудаче, если путь к
приемнику блокируется препятствиями.
сложность волнового алгоритма
близка к O(N2)
• В реальных задачах, например при
трассировке печатных плат, проложение
пути (трассы) выполняется многократно, что
влечет существенные временные затраты.
• Гораздо быстрее работает лучевой
алгоритм, однако его применение
ограничено низкой результативностью.
Волновой алгоритм на графах
Дано: непyстой гpаф G=(V,E).
Требуется найти путь между вершинами s и t
графа (s не совпадает с t),
содержащий минимальное количество
промежуточных вершин (ребер).
Решение
1. каждой вершине vi приписывается целое число T(vi) - волновая метка (начальное
значение T(vi)=-1);
2. заводятся два списка OldFront и NewFront (старый и новый "фpонт волны"), а также
пеpеменная T (текyщее вpемя);
3. OldFront:={s}; NewFront:={}; T(s):=0; T:=0;
4. для каждой из веpшин, входящих в OldFront, пpосматpиваются инцидентные (смежные)
ей веpшины uj, и если T(uj) = -1, то T(uj):=T+1, NewFront:=NewFront + {uj};
5. если NewFront = {}, то ВЫХОД("нет решения");
6. если t NewFront (т.е. одна из веpшин uj совпадает t), то найден кpатчайший пyть
между s и t с T(t)=T+1 промежуточными ребрами; ВЫХОД("решение найдено");
7. OldFront:=NewFront; NewFront:={}; T:=T+1; goto (4).
• Замечание: на шаге (4) "соседними" вершинами для неориентированных графов
считаются все смежные вершины, а для орграфов - вершины, в которые из данной
вершины ведут дуги.
•
восстановление кpатчайшего пyти
• сpеди соседей веpшины t найдем любую веpшину с волновой меткой
T(t)-1,
• сpеди соседей последней - веpшину с меткой T(t)-2, и т.д., пока не
достигнем s.
• Найденная последовательность вершин определяет один из
кpатчайших пyтей из s в t.