Содержание тем учебного курса № Кол-
реклама
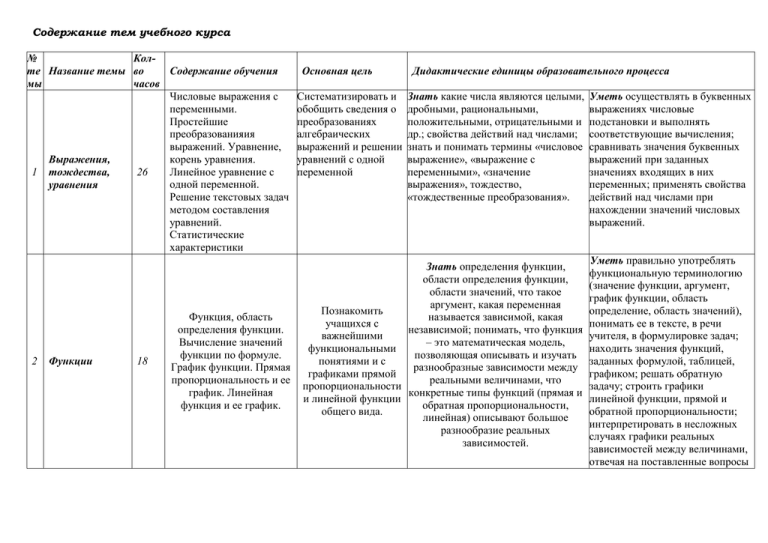
Содержание тем учебного курса № Колте Название темы во Содержание обучения мы часов Числовые выражения с переменными. Простейшие преобразованияия выражений. Уравнение, корень уравнения. Выражения, 1 тождества, 26 Линейное уравнение с одной переменной. уравнения Решение текстовых задач методом составления уравнений. Статистические характеристики 2 Функции 18 Функция, область определения функции. Вычисление значений функции по формуле. График функции. Прямая пропорциональность и ее график. Линейная функция и ее график. Основная цель Систематизировать и обобщить сведения о преобразованиях алгебраических выражений и решении уравнений с одной переменной Дидактические единицы образовательного процесса Знать какие числа являются целыми, дробными, рациональными, положительными, отрицательными и др.; свойства действий над числами; знать и понимать термины «числовое выражение», «выражение с переменными», «значение выражения», тождество, «тождественные преобразования». Знать определения функции, области определения функции, области значений, что такое аргумент, какая переменная Познакомить называется зависимой, какая учащихся с независимой; понимать, что функция важнейшими – это математическая модель, функциональными позволяющая описывать и изучать понятиями и с разнообразные зависимости между графиками прямой реальными величинами, что пропорциональности конкретные типы функций (прямая и и линейной функции обратная пропорциональности, общего вида. линейная) описывают большое разнообразие реальных зависимостей. Уметь осуществлять в буквенных выражениях числовые подстановки и выполнять соответствующие вычисления; сравнивать значения буквенных выражений при заданных значениях входящих в них переменных; применять свойства действий над числами при нахождении значений числовых выражений. Уметь правильно употреблять функциональную терминологию (значение функции, аргумент, график функции, область определение, область значений), понимать ее в тексте, в речи учителя, в формулировке задач; находить значения функций, заданных формулой, таблицей, графиком; решать обратную задачу; строить графики линейной функции, прямой и обратной пропорциональности; интерпретировать в несложных случаях графики реальных зависимостей между величинами, отвечая на поставленные вопросы 3 Степень с натуральным показателем 18 4 Многочлены 23 Уметь находить значения функций, заданных формулой, таблицей, графиком; решать обратную задачу; строить графики Степень с натуральным Выработать умение Знать определение степени, функций у=х2, у=х3; выполнять показателем и ее выполнять действия одночлена, многочлена; свойства действия со степенями с свойства. Одночлен. над степенями с степени с натуральным показателем, натуральным показателем; Функции у=х2 и у=х3 и их натуральными свойства функций у=х2, у=х3. преобразовывать выражения, графики. показателями содержащие степени с натуральным показателем; приводить одночлен к стандартному виду. Многочлен. Сложение, Выработать умение Знать определение многочлена, Уметь приводить многочлен к вычитание и умножение выполнять сложение, понимать формулировку заданий: стандартному виду, выполнять многочленов. Разложение вычитание, «упростить выражение», «разложить действия с одночленом и многочленов на умножение на множители». многочленом; выполнять множители. многочленов и разложение многочлена разложение вынесением общего множителя за многочленов на скобки; умножать многочлен на множители. многочлен, раскладывать многочлен на множители способом группировки, доказывать тождества. Формулы 5 6 7 Формулы сокращенного умножения Системы линейных уравнений Итоговое повторение a b 2 23 17 15 a 2 2ab b 2 , a b 3 a 3 3a 2 b 3ab 2 b 3 , a 2 b2 a ba b , 3 a b3 a ba 2 ab b2 Система уравнений. Решение системы двух линейных уравнений с двумя переменными и его геометрическая интерпритация. Решение текстовых задач методом составления систем уравнений. Актуализация опорных знаний учащихся учебного материала по алгебре 7 класса Выработать умение применять формулы сокращенного умножения в преобразованиях целых выражений в многочлены и в разложении многочленов на множители Ознакомить учащихся со способом решения систем линейных уравнений с двумя переменными, выработать умение решать системы уравнений и применять их при решении текстовых задач. Повторить, систематизировать и обобщить знания по курсу алгебры 7 класса. Знать формулы сокращенного умножения: квадратов суммы и разности двух выражений; различные способы разложения многочленов на множители. Знать, что такое линейное уравнение с двумя переменными, система уравнений, знать различные способы решения систем уравнений с двумя переменными: способ подстановки, способ сложения; понимать, что уравнение – это математический аппарат решения разнообразных задач из математики, смежных областей знаний, практики. Уметь читать формулы сокращенного умножения, выполнять преобразование выражений применением формул сокращенного умножения: квадрата суммы и разности двух выражение, умножения разности двух выражений на их сумму; выполнять разложение разности квадратов двух выражений на множители; применять различные способы разложения многочленов на множители; преобразовывать целые выражения; применять преобразование целых выражений при решении задач. Уметь правильно употреблять термины: «уравнение с двумя переменными», «система»; понимать их в тексте, в речи учителя, понимать формулировку задачи «решить систему уравнений с двумя переменными»; строить некоторые графики уравнения с двумя переменными; решать системы уравнений с двумя переменными различными способами. Закрепление знаний, умений и навыков, полученных на уроках алгебры за курс 7 класса по данным темам.