Алексеев-В.В.-Индивидуальное-задание-для-группы-ПМ
реклама
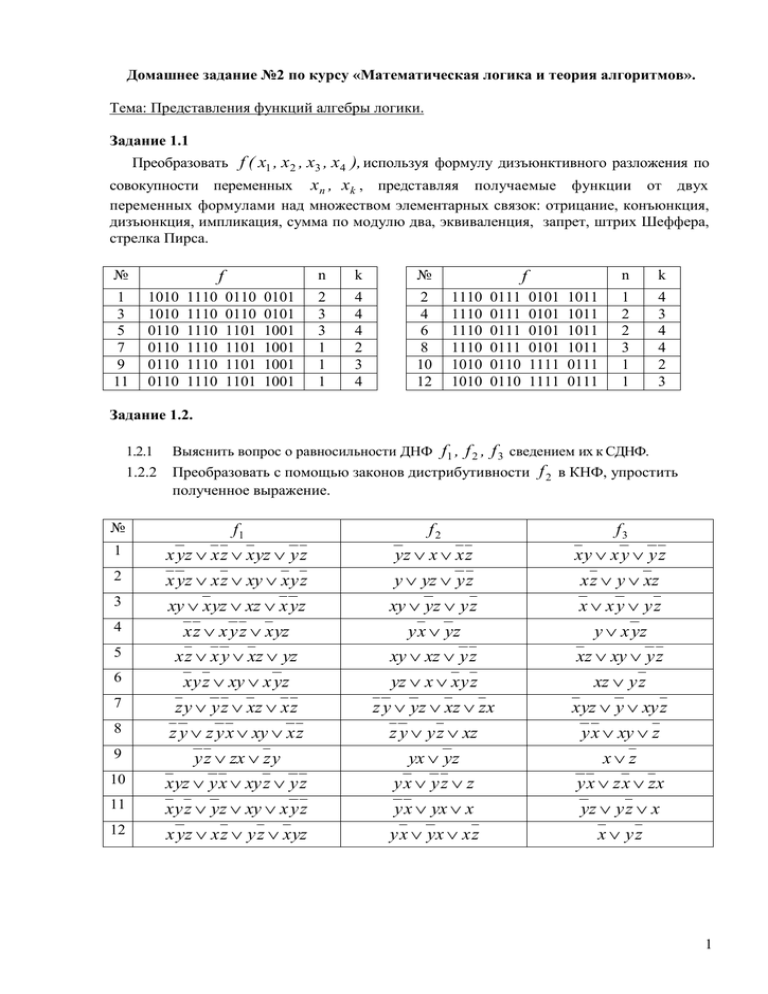
Домашнее задание №2 по курсу «Математическая логика и теория алгоритмов». Тема: Представления функций алгебры логики. Задание 1.1 Преобразовать f ( x1 , x2 , x3 , x4 ), используя формулу дизъюнктивного разложения по совокупности переменных xn , xk , представляя получаемые функции от двух переменных формулами над множеством элементарных связок: отрицание, конъюнкция, дизъюнкция, импликация, сумма по модулю два, эквиваленция, запрет, штрих Шеффера, стрелка Пирса. № 1 3 5 7 9 11 f 1010 1010 0110 0110 0110 0110 1110 1110 1110 1110 1110 1110 0110 0110 1101 1101 1101 1101 0101 0101 1001 1001 1001 1001 n k № 2 3 3 1 1 1 4 4 4 2 3 4 2 4 6 8 10 12 f 1110 1110 1110 1110 1010 1010 0111 0111 0111 0111 0110 0110 0101 0101 0101 0101 1111 1111 1011 1011 1011 1011 0111 0111 n k 1 2 2 3 1 1 4 3 4 4 2 3 Задание 1.2. 1.2.1 Выяснить вопрос о равносильности ДНФ f1 , f 2 , f 3 сведением их к СДНФ. 1.2.2 Преобразовать с помощью законов дистрибутивности f 2 в КНФ, упростить полученное выражение. № f1 f2 f3 1 x yz x z x yz y z yz x x z xy x y y z 2 x yz x z xy x y z y yz y z x z y xz 3 xy x yz xz x yz xy yz y z x xy yz 4 x z x y z x yz y x yz y x yz 5 x z x y xz yz xy xz y z xz xy y z 6 x y z xy x yz yz x x y z xz y z 7 z y y z xz x z z y yz xz zx x yz y xy z 8 z y z y x xy x z z y y z xz y x xy z 9 y z zx z y yx yz x z 10 x yz y x xy z y z yx yz z y x z x zx 11 x y z yz xy x y z y x yx x yz y z x 12 x yz x z y z x yz y x yx x z x yz 1 Задание 1.3 1.3.1. Для заданной функции найти полином Жегалкина. Решение представить двумя способами. 1.3.2. Найти СНДФ. 1.3.3. Найти СНКФ. № f № f № f 1 0111 1001 2 0101 1100 3 1000 0111 4 1100 0111 5 1110 1101 6 0110 0011 7 1001 0100 8 0010 1000 9 0111 1010 10 1011 0101 11 1010 1101 12 1101 0111 Тема: Замкнутые классы ФАЛ. (Классы Поста). Задание 2.1 2.1.1. Доопределить функции f(x,y,z), g(x,y,z), h(x,y,z) так, чтобы f M , g L , h S . Если построение какой-либо функции невозможно, докажите это. Выясните вопрос о принадлежности построенных функций к классам Т 0 и T1 . № 1 2 3 4 5 6 7 8 9 10 11 12 f (-1--011-) (-1--011-) (--11-0--) (-0-01---) (-1-1--0-) (-0-01---) (-01--0--) (-10---0-) (--11-0--) (---01-1-) (-1--0-0-) (-01--0--) g (01--1-0-) ( 0 1 - - 1 - 0 -) (-10-1-0-) ( 0 1- 1 - 0 - - ) (1--0-01-) (-1-01-01) (-01-1--0) (1---110-) (---110-1) (--0-00-1) ( 1 - - 0 -1 - 1 ) (---001-0) h (-101---0) (-101---0) (0--1-01-) (0-00--0-) (--01--11) (1 - - 0 - 1 0 - ) ( - 1 - 0- 0 - 1 ) (0--1-10-) (-1--10-0) (---1-010) (0-10--0-) (01--01--) Задание 2.2. 2.3.1. Для функций f(x,y,z) и g(x,y,z) выяснить вопрос об их принадлежности к классам T0, T1, L, S, M. 2.3.2. В случае, если некоторая функция представляет из себя функционально полный класс, выразить из неё с помощью суперпозиций константы 0,1, отрицание, дизъюнкцию x y и конъюнкцию xy. 2.3.3. Полученные результаты проверить с помощью построения таблиц. № 1 3 5 7 9 11 f 1111 0110 1000 1011 1111 1000 g 0100 1001 0010 1101 1010 0001 1001 1101 0000 1100 0101 1110 0110 0100 1101 0100 1111 1010 № 2 4 6 8 10 12 f 1100 0001 1001 1000 1011 0011 1000 1100 0001 0110 1100 1110 g 1101 1110 1100 0011 1111 1000 1110 1000 0110 1010 0010 0001 2