Задание на дом по теме: «Аксиомы стереометрии»
реклама

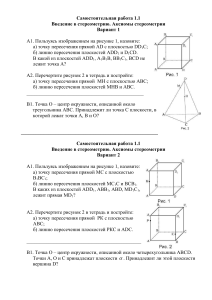
Задание на дом по теме: «Аксиомы стереометрии» Повторить аксиомы планиметрии, сделать эскиз плаката «Аксиомы планиметрии», подобный плакату «Аксиомы стереометрии», разобранному на уроке. Ответить на вопрос. Сколько положений в пространстве может занять дверь, побвешанная на одну петлю ,( на две петли), ( на две петли, и закрытая на замок ) ? Задача Дан куб ABCDAiBiCiDi Точка M лежит на ребре BBi, точка N лежит на ребре CCi и точка K лежит на ребре DDi а) Назовите плоскости, в которых лежат точки М; точка N. б) Найдите точку F – точку пересечения прямых MN и BC.Каким свойством обладает точкаF? в) Найдите точку пересечения прямой KN и плоскости ABC. г) Найдите линию пересечения плоскостей MNK и ABC. Творческое домашнее задание: Многолетний опыт работы со старшеклассниками показал, что многие не могут решить задачу по той причине, что им трудно представить то, о чем говорится в условии, построить чертеж объемной фигуры. Так родилась идея творческого домашнего задания по созданию конструктора. Для конструктора понадобятся: плитка потолочная пенопластовая, цветной картон, трубочки коктельные, гвоздики цветные, пыжи картонные, клей «Момент», папка целофановая с кнопкой, фломастеры, конверт большой почтовый. Плитку пенопластовую разрезаем на 4 части – это будут модели плоскостей. Цветные гвоздики вводим в коктельную трубочку с одной стороны и закрепляем с помощью клея «момент». На картонных кружках – пыжах с обеих сторон ярко пишем большие буквы латинского алфавита наиболее часто встречающиеся при решении задач. Из цветного картона вырезаем геометрические фигуры: круг, 2 прямоугольника, 4 треугольника разных видов, квадрат, параллелограмм, ромб, правильный шестиугольник. Каждый набор – конструктор содержит одну модель пенопластовой плоскости, 7 трубочек – отрезков с гвоздиком на одном конце. В почтовый конверт складываем 11 различных фигур и буквы. Конверты лучше пронумеровать. Теперь все складываем в папку и конструктор готов. Решая задачу ученик прежде строит объемную модель. Трубочки с гвоздиками хорошо держатся в пенопласте под любым наклоном. Заготовленные плоские фигуры – основания многогранников..