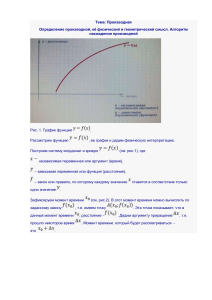
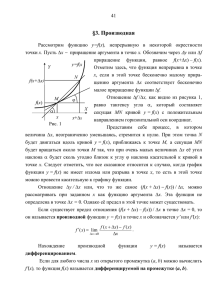
Решение. Δу = f(x 0 +Δx) – f(x 0 )
реклама

Производная функции Промежутки вида (а; b), ( - ∞; а), (а; +∞) называются интервалами. Окрестностью точки х0 называется любой интервал, содержащий эту точку. Например, окрестностью точки – 1 является интервал ( - 2; 0). Рассмотрим функцию у=f(x). Пусть х0 – фиксированная точка из области определения этой функции, х – произвольная точка из некоторой окрестности точки х0, причем х≠х0. Разность х – х0 называется приращением аргумента в точке х0. Приращение аргумента в точке х0 обозначается Δх. Δх=х – х0, откуда х=х0+Δх. Разность f(x) – f(x0) называется приращением функции в точке х0: Δу=f(x) – f(x0)=f(x0+Δх) – f(x0). Производной функции y=f(x) в точке х0 называется число, к которому ∆𝑦 стремится отношение при Δх, стремящемся к нулю. ∆𝑥 Производная функции y=f(x) обозначается f ‘ (x), у', 𝑓 ′ (𝑥0 ) = ∆𝑓 ∆𝑥 = 𝑑𝑦 𝑑𝑓(𝑥0 ) , . 𝑑𝑥 𝑑𝑥 𝑓(𝑥0 +∆𝑥)−𝑓(𝑥0 ) ∆𝑥 , при Δх0. ∆𝑓(𝑥0 ) ∆𝑥→0 ∆𝑥 Если этот предел конечный, то функция f(x) называется дифференцируемой (от латинского differentia – разность) в точке x0; при этом она оказывается обязательно и непрерывной в этой точке. 𝑓 ′ (𝑥0 ) = lim Если же рассматриваемый предел равен ∞ (или - ∞ ), то при условии, что функция в точке х0 непрерывна, будем говорить, что функция f(x) имеет в точке х0 бесконечную производную. Нахождение производной называется дифференцированием функции. Примеры решения задач Пример 1. Найти приращение функции f(x)=3x - 1 в точке х0, соответствующей приращению аргумента Δх. Решение. Δу= f(x0+Δх) – f(x0)=3(x0+Δх) -1-(3x0 – 1)=3Δх. Ответ: 3Δх Пример 2. Найти приращение функции f(x)=x2 и приращение аргумента Δх в точке х0=2, если х=1,9. Решение. Δх=х – х0=1,9 – 2= - 0,1. Δf= f(x0) – f(x)=f(1,9) – f(2)= =1,92 – 22= - 0,39. Ответ: Δх= - 0,1. Δf= - 0,39. Пример 3. Найти производную линейной функции y=kx+b. Решение. Δу = f(x0+Δx) – f(x0) = k(x0+Δx)+b - kx0- b = kΔx. ∆𝑦 𝑘∆𝑥 ∆𝑦 Найдем отношение = = 𝑘. Отношение не зависит от Δx, при ∆𝑥 ∆𝑥 ∆𝑥 любом значении Δx оно равно k. Следовательно, (𝑘𝑥 + 𝑏)′ = 𝑘. Ответ: (𝑘𝑥 + 𝑏)′ = 𝑘 Пример 4. Найти производную функции 𝑓(𝑥) = 𝑎𝑥 2 + 𝑏𝑥 + 𝑐. Решение. Δу = f(x0+Δx) – f(x0) = a(x0+Δx)2+b(x0+Δx)+c – (ax02+bx0+c) = = 2ax0Δx+a(Δx)2+bΔx. Найдем отношение Если Δх0, то ∆𝑦 ∆𝑥 ∆𝑦 ∆𝑥 = 2𝑎𝑥0 Δ𝑥+𝑎(Δ𝑥)2+𝑏Δ𝑥 ∆𝑥 = 2ax0+aΔx+b. 2ax0+b, т.е. f ‘(x0)=2ax0+b. Ответ: (𝑎𝑥 2 + 𝑏𝑥 + 𝑐)′ = 2𝑎𝑥 + 𝑏 4 Пример 5. Найти производную функции 𝑓(𝑥) = . Решение. Δу = f(x0+Δx) – f(x0) = Найдем отношение 4 ′ 𝑓 ′(𝑥) = ( ) = 𝑥 ∆𝑦 ∆𝑥 4 𝑥0 +∆𝑥 −4 = (𝑥0 +∆𝑥)𝑥0 − 4 𝑥0 = 𝑥 −4∆𝑥 (𝑥0 +∆𝑥)𝑥0 ∆𝑦 . При Δх0 ∆𝑥 . −4 𝑥0 2 . Следовательно, −4 𝑥2 4 ′ Ответ: ( ) = 𝑥 −4 𝑥2 Пример 6. Найти производную функции 𝑓(𝑥) = √𝑥. Решение. 𝑓 ′(𝑥) = ∆𝑦 ∆𝑥 1 2√𝑥0 ∆𝑓 ∆𝑥 = 𝑓(𝑥0 +∆𝑥)−𝑓(𝑥0 ) ∆𝑥 1 ′ . Следовательно, (√𝑥) = = √𝑥0 +∆𝑥−√𝑥0 ∆𝑥 = 1 √𝑥0 +∆𝑥+√𝑥0 . При Δх0 2√𝑥 ′ Ответ: (√𝑥) = 1 2√𝑥 Упражнения 1. Найдите приращение Δу функции f(x) в точке х0, если: 2 6 1) 𝑓(𝑥) = − , 𝑥0 = −2, ∆𝑥 = 0,1 2) 𝑓(𝑥) = − , 𝑥0 = 1, ∆𝑥 = 0,6 3) 𝑓(𝑥) = 4 − 3𝑥 2 , 𝑥0 = 5, ∆𝑥 = −0,6 4) 𝑓(𝑥) = 2𝑥 2 − 3, 𝑥0 = 3, ∆𝑥 = −0,2 𝑥 𝑥 1 5) 𝑓(𝑥) = 3𝑥 + 1, 𝑥0 = 5, ∆𝑥 = 0,01 6) 𝑓(𝑥) = 2𝑥 2 + 1, 𝑥0 = , ∆𝑥 = −0,8 7) 𝑓(𝑥) = 5𝑥 + 2, 𝑥0 = 0,2, ∆𝑥 = 0,5 8) 𝑓(𝑥) = 4 2 𝑥2 2 , 𝑥0 = 2, ∆𝑥 = 0,1 10) 𝑓(𝑥) = 4 − 3𝑥, 𝑥0 = −1, ∆𝑥 = 0,4 9) 𝑓(𝑥) = − 1, 𝑥0 = −2, ∆𝑥 = −0,9 𝑥 2. Найдите приращение Δx аргумента и приращение функции Δу в точке х0, если: 1) 𝑓(𝑥) = cos 2 𝑥, 𝑥0 = 2𝜋 3 ; 𝑥= 3𝜋 4 𝑥 2 𝜋 𝜋 4 3 6) 𝑓(𝑥) = 𝑥 + 𝑥 2 , 𝑥0 = 2,1; 𝑥 = −1,3 7) 𝑓(𝑥) = √2𝑥 − 1, 𝑥0 = 1,22; 𝑥 = 1,345 9) 𝑓(𝑥) = 𝑥2 6 4 4) 𝑓(𝑥) = 4𝑥 − 𝑥 2 , 𝑥0 = 2,5; 𝑥 = 2,6 3) 𝑓(𝑥) = 5 − , 𝑥0 = −2,4; 𝑥 = 1,2 5) 𝑓(𝑥) = 𝑡𝑔 𝑥, 𝑥0 = ; 𝑥 = 𝑥 𝑓(𝑥) = + 8, 𝑥0 = −4,9; 𝑥 = 2) −3,4 − 𝑥, 𝑥0 = −1,8; 𝑥 = 0,4 𝜋 2𝜋 3 3 8) 𝑓(𝑥) = sin2 𝑥, 𝑥0 = ; 𝑥 = 10) 𝑓(𝑥) = 𝑥2 3 − 𝑥, 𝑥0 = 1,5; 𝑥 = 0,5 3. Пользуясь определением производной, найдите значение производной функции в точке a: 1) 𝑓(𝑥) = 3, 𝑎 = 10 𝑥 2) 𝑓(𝑥) = 4𝑥, 𝑎 = 1 3) 𝑓(𝑥) = 1 − , 𝑎 = 0 4) 𝑓(𝑥) = −2,5𝑥 − 2, 𝑎 = −2 5) 𝑓(𝑥) = −6, 𝑎 = 1 6) 𝑓(𝑥) = −5𝑥, 𝑎 = 7 7) 𝑓(𝑥) = 𝜋, 𝑎 = −4 8) 𝑓(𝑥) = 2 + 9) 𝑓(𝑥) = √8, 𝑎 = −5 10) 𝑓(𝑥) = −4,2𝑥 + 3, 𝑎 = −6 2 3𝑥 4 , 𝑎=1 4. Пользуясь определением производной, найдите значение производной функции в точке a: 1) 𝑓(𝑥) = (3 + 𝑥)2 , 𝑎 = −2 3) 𝑓(𝑥) = 𝑥2 6 − 0,2𝑥 + 8, 𝑎 = 3 2) 𝑓(𝑥) = 4) 𝑓(𝑥) = 6−6𝑥−12𝑥 2 6 4𝑥 2 5 − 𝑥 10 , 𝑎 = −3 + 1, 𝑎 = −1 5) 𝑓(𝑥) = 𝑥 2 − 𝑥 = 2, 𝑎 = 0 6) 𝑓(𝑥) = (3 − 𝑥)2 , 𝑎 = −1,5 7) 𝑓(𝑥) = 𝑥 2 − (𝑥 + 2)2 , 𝑎 = −0,5 8) 𝑓(𝑥) = 𝑥(𝑥 − 4), 𝑎 = 1 9) 𝑓(𝑥) = 6𝑥 2 −3𝑥+9 3 10) 𝑓(𝑥) = 𝑥 2 + 3𝑥 − 1, 𝑎 = 0,25 , 𝑎 = −2 5. Пользуясь определением производной, найдите значение производной функции в точке a: 5 2) 𝑓(𝑥) = √𝑥, 𝑎 = 0,01 1) 𝑓(𝑥) = , 𝑎 = 0,1 𝑥 1 4) 𝑓(𝑥) = √4𝑥, 𝑎 = 0,04 3) 𝑓(𝑥) = 𝑥 + , 𝑎 = 0,2 𝑥 1 6) 𝑓(𝑥) = √9𝑥 + 1, 𝑎 = 1 5) 𝑓(𝑥) = − + 1, 𝑎 = −1 𝑥 3 8) 𝑓(𝑥) = −√0,01𝑥, 𝑎 = 100 7) 𝑓(𝑥) = + 𝑥 2 , 𝑎 = 52 𝑥 2 6 9) 𝑓(𝑥) = 3 − , 𝑎 = −0,5 10) 𝑓(𝑥) = − , 𝑎 = −0,1 𝑥 𝑥 6. Решите уравнение f ‘(x)=0: 1) 𝑓(𝑥) = 𝑥 2 − 4𝑥 2) 𝑓(𝑥) = (𝑥 − 4)2 3) 𝑓(𝑥) = 𝑥 4 + 4𝑥 4) 𝑓(𝑥) = 𝑥 4 − 12𝑥 2 5) 𝑓(𝑥) = 2𝑥 4 − 𝑥 8 6) 𝑓(𝑥) = 𝑥 2 + 2𝑥 7) 𝑓(𝑥) = (2 − 𝑥)2 − 4 8) 𝑓(𝑥) = 𝑥 4 − 2𝑥 2 + 1 9) 𝑓(𝑥) = − 3 2 3 2 𝑥2 5 + 10𝑥 3 3 1 10) 𝑓(𝑥) = 𝑥 5 − 3 𝑥 3 + 5𝑥 3 7. Решите неравенство f ‘(x)≤0, если: 1) 𝑓(𝑥) = 5𝑥 2 + 𝑥 + 2 4) 𝑓(𝑥) = 7) 𝑓(𝑥) = √𝑥 4 5) 𝑓(𝑥) = 1+𝑥 √𝑥−3 4 √𝑥 2 5 𝑥−2 8) 𝑓(𝑥) = 2𝑥 3 − 3𝑥 2 10) 𝑓(𝑥) = 2) 𝑓(𝑥) = 3) 𝑓(𝑥) = 3𝑥 2 + 2𝑥 6) 𝑓(𝑥) = −𝑥 2 + 4𝑥 − 1 2 9) 𝑓(𝑥) = − 𝑥 𝑥 +1 8. Задайте функцию формулой, если производная этой функции равна: 1 1) 2 2) - 6 3) x+1 4) 6) 2x 7) - x 8) x - 1 9) 4 − 2 √𝑥 +2 1 √𝑥 5) 2х+2 10) 1 √𝑥 +3 − 9𝑥