Математика» для студентов 1 курса всех специальностей
реклама
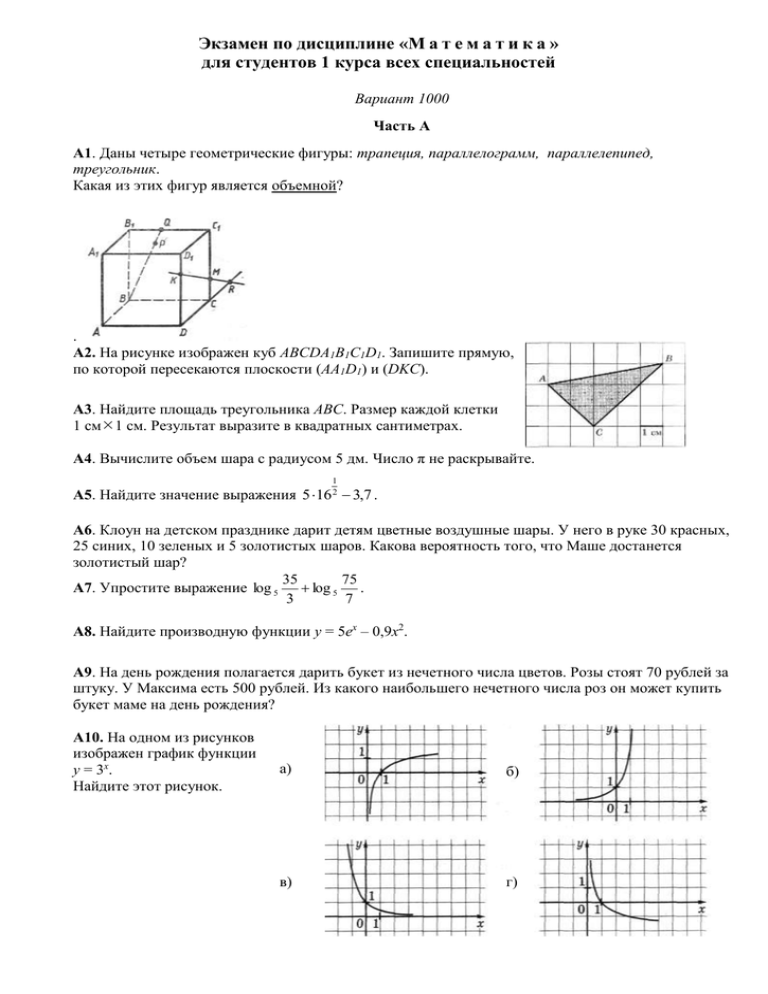
Экзамен по дисциплине «М а т е м а т и к а » для студентов 1 курса всех специальностей Вариант 1000 Часть А А1. Даны четыре геометрические фигуры: трапеция, параллелограмм, параллелепипед, треугольник. Какая из этих фигур является объемной? . А2. На рисунке изображен куб ABCDA1B1C1D1. Запишите прямую, по которой пересекаются плоскости (AА1D1) и (DKC). А3. Найдите площадь треугольника АВС. Размер каждой клетки 1 см1 см. Результат выразите в квадратных сантиметрах. А4. Вычислите объем шара с радиусом 5 дм. Число π не раскрывайте. 1 А5. Найдите значение выражения 5 16 2 3,7 . А6. Клоун на детском празднике дарит детям цветные воздушные шары. У него в руке 30 красных, 25 синих, 10 зеленых и 5 золотистых шаров. Какова вероятность того, что Маше достанется золотистый шар? 35 75 А7. Упростите выражение log 5 log 5 . 3 7 А8. Найдите производную функции у = 5ех – 0,9х2. А9. На день рождения полагается дарить букет из нечетного числа цветов. Розы стоят 70 рублей за штуку. У Максима есть 500 рублей. Из какого наибольшего нечетного числа роз он может купить букет маме на день рождения? A10. На одном из рисунков изображен график функции у = 3х. Найдите этот рисунок. а) б) в) г) А11. Упростите выражение: tgx ctgx 10 . А12. На диаграмме показана среднемесячная Температура воздуха в Санкт-Петербурге за каждый месяц 2011 года. По горизонтали указаны месяцы, а по вертикали – температура в градусах Цельсия. Определите по диаграмме, сколько месяцев второго полугодия 2011 года средняя температура была ниже 14 градусов Цельсия. А13. Трое друзей решают, как дешевле доехать из Москвы в Санкт-Петербург – на поезде или в автомобиле. Билет на поезд стоит 600 рублей на одного человека. Автомобиль расходует 10 литров бензина на 100 км пути. Расстояние по шоссе равно 750 км, а цена бензина равна 21 руб. за литр. Сколько рублей придется заплатить за наиболее выгодную поездку втроем? Часть В В1. На рисунке изображен график производной некоторой функции y = f(x), заданной на отрезке [-6;5]. Определите по графику количество промежутков убывания. В2. Решите показательное уравнение7х+2 − 14.7х =5. В3. Решите логарифмическое неравенство log 1 2 x 3 > −2. 5 у 3 9 х 2 6 х 1, В4. Пусть (х0; у0) – решение системы Найдите значение выражения х0 − 5у0. у 3х 10. В5. Найдите значение выражения 169 sin 2 x, если sin x 12 3 , x 2 . 13 2 Часть С С1. Проведите полное исследование и постройте график функции f x x 4 4x 2 . С2. Четная функция y = f(x) определена на всей числовой прямой. Для функции f x 9,5 g x 3,1 вычислите сумму g(9) + g(10). x 9,5 С3. Решите уравнение 29 х 9 37 х 3 56 х 720 х 3 .