Описание задания для «Компьютерной страны»

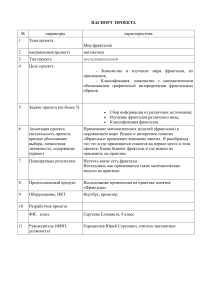
Клуб программистов
Задание для дистанционного тура
За отведенное время с 15.00. 7.04.2003 по 17.00. 8.04.2003. (время московское)
предлагается построить фрактал по описанию, «цветной» вариант с обоснованием способа
раскраски – дополнительные баллы. Принимаются также программы для построения
любых фракталов со ссылкой на литературу, в которой приведены их (фракталов)
описания.
По окончании работ не позднее 17.00. (время московское) 8.04.2003. в оргкомитет
фестиваля festival@samlit.samara.ru необходимо выслать письмо, содержащее:
 Тема письма - Клуб программистов,
 Тело письма: задание дистанционного тура члена клуба программистов
фамилия, имя, учебное заведение,
 Вложение: zip-архив, назван файл этого zip-архива по фамилии
программиста.
В zip-архиве необходимо представить:
1. Исходный код программы с комментариями. Основные фрагменты алгоритмов
должны быть прокомментированы подробно.
2. Исполняемый файл (программа).
3. Описание установки программы.
4. Авторский комментарий на тему «Как использовать программу».
5. Программа должна быть работоспособной.
6. Пользователь должен иметь возможность изменять входные данные (задавать
начальные точки, число итераций, менять другие параметры.)
Примечание.
Программа не должна требовать установки в строго определенный каталог и / или
наличия дополнительного программного или аппаратного обеспечения.
Уровень А.
Построить фрактал, последовательно заменяя фигуру из 4 отрезков, которая
изображена слева на рисунке, фигурой из 8 отрезков, изображенных справа (пунктиром
показана прежняя фигура).
Уровень В.
Пусть преобразования координат заданы так:
X  A(i)*X + B(i) * Y + E(i);
Y  C(i)*X + D(i)* Y + F(i);
где i меняется от 1 до n (заранее заданного числа). Если, к примеру, i=3, то для
преобразования x и y существует три правила, которые применяются по очереди. Сначала
получают и строят новые точки по первому правилу, потом – по второму и, наконец, по
третьему.
Разумеется, для получения «красивых» рисунков придется подбирать параметры.
Приветствуется возможность задавать параметры и начальные точки изображения
во внешних файлах.
Критерии оценки созданной программы:
Базовая шкала: 0, 1, 2, 3 балла.
1. Оригинальность алгоритма.
2. Скорость работы.
3. Оформление кода (комментарии и т.п.).
4. Документация (ссылки на литературу и пр.).
5. Обработка ошибок, интерфейс.
Дополнительные баллы могут быть начислены
 за раскраску фрактала (+1 балл),
 за обоснование алгоритма раскраски (+2 балла),
 программам генерирующим построение других фракталов (д.б.
представлены как исходные коды, так и исполняемые файлы) (до 2
баллов)
P-S. Как известно, математика – это тот универсальный язык, на котором «говорят»
практически все науки. И потому даже очень далекие друг от друга области научного
знания оказываются похожими в идейном плане. Более того, границы между
традиционными дисциплинами становятся менее отчетливыми, возникает понятие
«динамики сложных систем». Ученые, занимающиеся этими вопросами, находят материал
для исследований при изучении физических, химических, биологических явлений, при
анализе закономерностей социального поведения или психологии восприятия. Например,
немецкий ученый Г. Хакен, один из основателей теории лазеров, обнаружил, что
образование внутренних структур в лазерах и конкуренция молекулярных видов
подчиняются очень схожим законам.
Изменилось восприятие такого понятия как «хаос». Когда говорят о «хаотической
динамике», имеют в виду, что невозможно предсказать поведение системы (хотя сама
система при этом описывается вполне определенными законами). Выяснилось, что
существуют сценарии превращения порядка в хаос, которые действуют всегда. Вообще
задачи, о которых мы ведем речь, могут быть описаны как конкуренция нескольких
центров за доминирование на плоскости. В результате этой борьбы за территорию
возникают границы самой причудливой формы. И именно в этих пограничных областях
происходит переход от порядка к беспорядку. При моделировании плоскость обычно
считают бесконечной, что является идеализацией. В реальности, конечно же, не
существует структур, способных бесконечно увеличиваться.
Вместе с тем, в природе мы можем наблюдать повторения одного и того же узора,
увеличенного или уменьшенного во много раз. Одним из примеров может послужить
дерево. У дерева есть ветви, от этих ветвей отходят ветви поменьше и т.д. Леонардо да
Винчи даже высказывал предположение, что все ветки дерева на данной высоте,
сложенные вместе, равны по толщине стволу. Получается, что элемент «разветвление»
повторяется много раз, становясь меньше и меньше. Такое свойство называют
самоподобием. Увидеть самоподобие можно в береговых линиях водоемов (вспомните о
фьордах), в очертаниях облаков или гор, в живых системах.
Процессы, которые приводят к образованию самоподобных структур, – это так
называемые процессы с обратной связью. В таких процессах одна и та же операция
повторяется снова и снова, и результат одной итерации служит начальными данными для
следующей. Единственное, что требуется для возникновения таких структур, – закон,
описывающий переход от одной итерации к другой xn+1 = f(xn) должен быть более
сложным, чем простая пропорциональность вида xn+1 = k*xn.
Множества, части которых являются повторением самих множеств, называются
фракталами (этот термин ввел Б. Мандельброт). Построение таких множеств является
само по себе нетривиальной задачей. И чрезвычайно красивые картины можно получить,
тщательно продумав раскраску.
Литература.
1. Есипов А.С., Паньгина Н.Н., Громада М.И. Информатика. Сборник задач и
решений для общеобразовательных заведений. – СПб.: Наука и Техника, 2001.
2. Вирт Н. Алгоритмы и структуры данных. – СПб.: Невский диалект, 2001.
3. Пайтген Х.–О., Рихтер П.Х. Красота фракталов. Образы комплексных
динамических систем. – М.: Мир, 1993.