Использование симметрии аналитических выражений
реклама

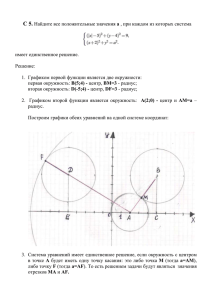
Задание 1. Найти все значения параметра a , при каждом из которых система 3 2 x 5 x 4 3 y 5 x 2 3a, имеет единственное решение. 2 2 x y 1. Решение Прежде, чем начать решать систему, что можно заметить: 1. x 1 , y 1 ; 2. Система симметрична относительно переменной x, а это значит, если пара x0 ; y 0 является решением системы, то x0 ; y 0 тоже её решение; 3. Для единственности необходимо выполнение условия x0 x0 , x0 0 . Подставим и найдем значения параметра 3 2 0 5 0 4 3 y 0 3a, 3 y 7 3a 0, 2 2 y 1. y 1. 3 y 7 3a 0, 3 y 7 3a 0, или y 1. y 1. Решая эти две системы найдём а. a 4 10 или a 3 3 Можно ли записать ответ? Нет. 1. Учитель добивается от учащихся, что бы они пришли к выводу; что это необходимые значения параметра, а их достаточность нужно проверить 4 При a , система имеет вид 3 x 3 2 5 x 3 y 5 x 2 , 2 2 x y 1. Вспомним, что в начале решения мы уже отметили, что 1 x 1, 1 y 1 , учитывая это, попробуем сравнить правую и левую части первого уравнения системы. x x 2 1, т. е. 2 y x x 2 , значит и 3 2 x 5 x 3 y 5 x 2 , причем равенство наступает при условии x 0 , y 1 . Поэтому a При a 4 следует записать в ответ. 3 10 , исходная система имеет вид 3 3 2 x 5 x 3 y 5 x 2 6, 2 2 x y 1. Доказать единственность тем же путем невозможно. Но есть и другие пути. Какие? Можно найти более чем одно решение. x 0 , y 1 видим что это решение, но и x 1, y 0 тоже решение последней 10 системы. Значит, a не удовлетворяет требованиям исходной системы. 3 Ответ: a 4 . 3 Задание 2. Найти все значения параметра a , при которых система y y 3 2 2 3 2 2 3a x 2 6 x 5, имеет единственное решение. y 2 a 2 5a 6 x 2 0, 6 x 0. Решение Заметим, что 3 2 2 y 1 3 2 2 y y 3 2 2 . Отсюда можно сделать вывод. 1. Данная система симметрична относительно переменной y . Поэтому, если x0 ; y 0 решение исходной системы, то и пара x0 ; y 0 – также решение этой системы. 2. Для единственности решения необходимо выполнение условия y0 y0 , y0 0 2 3a x 2 6 x 5, При y 0 , получим x 2 a 2 5a 6 0, 6 x 0. Если x 2 0 , x 0 , то подставим это значение в первое уравнение последней системы, получим 2 3a 5 , a 1 . Если a 2 5 6 0, a1 2 , a 2 3 . 3. Получим список “кандидатов” в ответ: a 1 , a 2 , a 3 , который нужно проверить. При a 1 получаем систему 3 2 2 y 3 2 2 y 3 x 2 6 x 5, y 2 12 x 2 0, 6 x 0. Если x 6;0 , то x 2 6 x 5 5 . y y 1 1 t 2 , при t 0 , тогда В то же время 3 2 2 t , 3 2 2 , t t 3 2 2 3 2 2 y y 3 5. Тогда, если полученная система имеет решение, то им может быть только пара 0;0 . Действительно 0;0 подходит. При a 2 получаем систему: 3 2 2 y 3 2 2 y 6 x 2 6 x 5, y 2 0, 6 x 0. имеющую единственное решение 3;0 . 32 2 При a 3 возникает система: y 0, 2 x 6 x 9 0, 6 x 0. 3 2 2 y y y 0, x 3, 6 x 0. 9 x 2 6 x 5, y 2 0, 6 x 0. x 2 6 x 12 0, y 0, 6 x 0. Уравнение x 2 6 x 12 0 не имеет решений, значит и система не имеет решение. Ответ: a 1 , a 2 . Самостоятельная работа Задание 1. Найти все значения параметра a , при каждом из которых система 5 2 x 3 x 2 5 y 3 x 2 5a, имеет единственное решение. x 2 y 2 1. Задание 2. Найти все значения параметра a , при которых система 2 3 x 2 3 x 5 a 2y y2 , имеет единственное решение. x 2 2 a a 2 y 2 0, 0 y 2. Домашнее задание 2 x x y x 2 a , Задание 1. При каких a система 2 имеет единственное 2 x y 1. решение? Решение самостоятельной работы. 5 2 x 3 x 2 5 y 3 x 2 5a, x 2 y 2 1. Система симметрична относительно переменной x . 5 2 5 y 5a, 3 5 y 5a, x 0 2 y 2 1. y 1. 5a 5 y 3, 5a 5 y 3, или y 1. y 1. 2 8 или a . 5 5 Проверим достаточность найденных значений. 5 2 x 3 x 2 5 y 3 x 2 2, 2 При a получаем систему 5 x 2 y 2 1. Решая эти системы получим a 2 x 1, y 1 , x x x 2 , т.к. x 1 , тогда 5 2 3 x 5 y 3x 2 , причем достигается при значит 2 x y , условии x 0 , y 1 . Значит пара 0;1 решение системы. 5 2 x 3 x 2 5 y 3x 2 8, x 2 y 2 1. Доказать единственность этой системы трудно, но можно найти более, чем одно решение. 0;1 решение системы, но и 1;0 тоже решение этой системы. Значит 8 a не удовлетворяет требованиям исходной задачи. 5 2 Ответ: a . 5 При a 8 получаем систему 5 Задание 2. Найти все значения параметра a , при каждом из которых 2 3 x 2 3 x 5 a 2y y2 , система имеет единственное решение. x 2 2 a a 2 y 2 0, 0 y 2. Решение 2 3 1 2 3 3 2 3 1 , значит данную систему можно записать так : x 2 3 x 2 5 a 2y y2 , x 2 2 a a 2 y 2 0, 0 y 2. Система симметрична относительно переменной x . Чтобы исходная система имела единственное решение, необходимо x 0 , тогда исходная система принимает вид: 1 1 5 a 2 y y 2 , 2 2 2 a a y 0, 0 y 2. Если y 0 , то из первого уравнения системы a 3 . Если 2 a a 2 0 , то a1 1 , a2 2 Достаточность проверим, подставив найденные значения в исходную систему. Ответ: a 3 , a 2 .