Быстрый счёт без калькулятора. Правда или миф

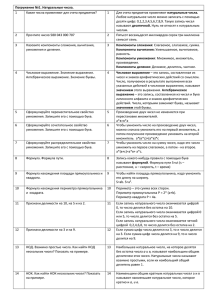
Фамилия, имя автора статьи: Никифорова Анастасия
Класс: 6
Название ОУ:
Муниципальное бюджетное общеобразовательное учреждение
«Средняя общеобразовательная школа» г. Югорска, ХМАО-Югра
Фамилия, имя, отчество руководителя: Никифорова Марина Владимировна
Тема работы: «Быстрый счёт без калькулятора: правда или миф…»
e-mail: mvnikif@yandex.ru
Как правило, чтобы быстро что-то сосчитать – мы используем калькулятор и
уже практически отвыкли от мысли о том, что способны это делать самостоятельно.
Зачем ломать голову, когда лучше нажать пару кнопок и результат будет гораздо
быстрее и точнее? Безусловно – так проще, однако это нас никоим образом не
развивает, а скорее даже наоборот. Впервые с приёмом быстрого счёта нас
познакомили на уроках математики в 5 классе – это приём умножения чисел на 11.
Мне стало интересно, какие приемы быстрого счёта ещё существуют?
В истории математики известно около 30 общих способов умножения,
отличающихся либо схемой записи, либо самим ходом вычисления. Принятый у нас
обычный способ умножения является наиболее удобным для преподавания, но
совсем не лучшим в применении. Также существуют и признаки делимости чисел, и
правила сложения и вычитания, которые ускоряют выполнение этих
арифметических действий.
Цель работы: изучение и исследование методов и приемов быстрого счета и
создание книжки-памятки для школьника, содержащую эти приёмы.
Для достижения цели работы необходимо решить следующие задачи:
воспользовавшись различными источниками информации собрать, изучить и
систематизировать материал о приемах устного счета, рассмотреть некоторые
приемы устного счета и на конкретных примерах, показать преимущества их
использования, создать книжку-памятку для школьника, содержащую приёмы
быстрого устного счёта.
Продукт проекта: сборник приёмов и методов быстрого устного счёта.
Используемые методы: обзор литературы, аналитический метод,
социологический опрос, статистическая обработка данных опроса, графический
метод.
Практическая значимость исследования заключается в формировании
умений и навыков быстрого устного счёта у учащихся. Собранные материалы
(сборник приёмов быстрого счёта, презентация проекта) может быть использованы
учителями математики, физики и учащимися на уроках.
Приёмы быстрого устного счёта
1. Умножение двузначных чисел, близких к 100.
Всякое двузначное число можно представить в виде 100—а. Будем называть а
недостатком данного числа до 100. Если данные числа близки к 100, то недостатки
их — сравнительно небольшие числа, удобные для устных вычислений. Рассмотрим
такое умножение в общем виде: (100 – а) (100 – b) = 100×100 – 100а – 100b +аb =
(100 –а – b)100+аb. Это выражение показывает: чтобы получить число сотен
искомого произведения, достаточно из одного сомножителя (например, 100—а)
вычесть недостаток другого сомножителя (т. е. b) и к полученной разности
приписать произведение недостатков аb, если аb — число двузначное. Если аb —
однозначное число, например 8, то приписывается 08. Умножить 87 на 94. Первый
недостаток 13, второй 6. Из 87 вычитаем 6 (или из 94 вычитаем 13), получаем 81. К
81 приписываем 13-6 = 78. Произведение 8178. Идею этого интересного способа
легко распространить и на умножение двух трехзначных чисел, близких к 1000.
Умножим, например, 985 на 992. Первый недостаток 15, второй 8. Вычитая 8 из 985
(или 15 из 992), получим 977 — число тысяч искомого произведения. Приписав к
977 произведение недостатков 15-8 = 120, получим произведение 977 120.
2. Умножение и деление на 4.
Чтобы число умножить на 4, его дважды удваивают. Например: 213*4 = 213*2*2 =
426*2 = 852. Чтобы число разделить на 4, его дважды делят на 2.
Например:124:4 = (124:2):2 = 62:2 = 31.
Признаки делимости на 4:- число делится на 4, если на 4 делится число,
состоящее из последних двух цифр числа.
Например: 1836, число 36:4 = 4, значит 1836 делится на 4.
Число 17833 на 4 не делится, так как на 4 не делится число 33.
4. Умножение и деление на 5.
Чтобы число умножить на 5, его надо сперва умножить на 10, а потом разделить на
5.
138*5 = (138*10):2 = 1380:2 = 690
Чтобы разделить число на 5, нужно его разделить на 10 и умножить на 2, или
умножить на 0,2, т.е. в удвоенном исходном числе отделить запятой последнюю
цифру.
345:5 = 345:10*2 = 34,5*2 = 69, 71:5 = 71*0,2 = 71*2:10 = 14,2
5. Умножение и деление на 6.
Чтобы умножить число на 6, надо: 1-ый способ: последовательное умножение –
сперва умножить на 3, затем умножить на 2
48*6 = 48*3*2 = 144*2 = 288
2-ой способ – представление числа 6 в виде суммы 5+1 и использование
распределительного закона умножения:
48*6 = 48*(5+1) = 48*5 + 48*1 = (48*10:2) + 48 = 240 + 48 = 288
Признак делимости на 6: Число делится на 6, если сумма цифр числа делится на 6.
327 делится на 6, так как 3 + 2 + 7 = 12 делится на 6,
341 не делится на 6, так как 3 + 4 + 1 = 8 не делится на 6.
6. Умножение на 7.
При умножении числа на семь, 7 представляется в виде суммы 5+2.
97*7 = 97* (5 + 2) = 97*5 + 97*2 = 97*10:2 + 97*2 = 485 + 194 = 679
7. Умножение на 8.
При умножении на 8 можно пользоваться двумя приёмами:
1. Последовательное умножение: 48 * 8 = 48 * 2* 2* 2
2. 8 представляется в виде разности (10 – 2): 127 * 8 = 127 * (10 – 2) = 127*10 –
127*2 = 1270 – 254 = 1016
8. Умножение на 9.
Чтобы умножить число на 9, к нему приписывают 0 и отнимают исходное число.
241*9 = 2410 – 241 = 2169
Признак делимости на 9: Число делится на 9, если сумма цифр числа делится на 9.
928 делится на 9, так как 9 + 2 + 8 = 18 делится на 9,
323 не делится на 9, так как 3 + 2 + 3 = 8 не делится на 9.
9. Умножение на 11.
1. Чтобы умножить число на 11, к нему приписывают 0 и прибавляют исходное
число.
47 * 11 = 47 * 10 + 47 = 470 + 47 = 517
2. Мысленно цифры этого числа раздвинуть. Сложить цифры, записать полученную
сумму между раздвинутыми цифрами.
35 * 11 = 3(3+ 5)5 = 385
47 * 11 = 4(4+7)7 = 4(11)7 = 517
10. Умножение и деление на 25.
Чтобы число умножить на 25, нужно умножить его на 100 и разделить на 4.
348 * 25 = 348 * 100 : 4 = 34800 : 2 : 2 = 8700
Чтобы число разделить на 25, его надо умножить на 4 и разделить на 100.
8700 : 25 = 8700 * 4 : 100 = 34800 : 100 = 348
11. Умножение на 1,5.
Чтобы умножить число на 1,5, нужно к исходному числу прибавить его половину.
129 * 1,5 = 129 + 129 : 2 = 129 + 64,5 = 193,5
12. Возведение в квадрат числа, оканчивающегося цифрой 5.
Есть
замечательный способ возведения в квадрат двузначных чисел,
оканчивающихся цифрой 5. Для возведения такого числа в квадрат надо умножить
цифру десятков на следующую за ней цифру, а 5 возвести в квадрат и приписать
результат – 25 после полученного произведения.
Например, 35²=1225 (так как 3∙4=12); 85²=7225 (так как 8∙9=72).
Возведение в квадрат двухзначных и трёхзначных чисел: умножают число
десятков на число, на единицу больше, и к произведению приписывают 25.
752=(7∙8) в конец произведения подписываем 25 =5625
13. Умножение чисел от 10 до 20.
К одному из чисел надо прибавить количество единиц другого, умножить на 10 и
прибавить произведение единиц чисел.
16 * 18 = (16 + 8) *10 + 6*8 = 288
14. Умножение чисел на 22, 33, 44, ….99.
Чтобы двузначное число умножить на 22, 33, …, 99, надо этот множитель
представить в виде произведения однозначного числа (от 2 до 9) на 11, то есть 44 =
4*11; 55 = 5*11 и т.д. Затем произведение первых чисел умножить на 11.
18 * 44 = 18 * 4 * 11 = 72 * 11 = 7(7+2)2 = 792
15. Способы быстрого сложения и вычитания.
Если одно из слагаемых увеличить на несколько единиц, а второе уменьшить на
столько же единиц, то сумма не изменится. 762 + 639 = (762 + 8) + (639 – 8) = 770 +
631 = 1401
Если одно из слагаемых увеличить на несколько единиц, то из полученной суммы
надо вычесть столько же единиц. 785 + 963 = 785 + (963 + 7) – 7 = 785 + 970 – 7 =
1748
Если вычитаемое уменьшить на несколько единиц и уменьшаемое увеличить на
столько же единиц, то разность не изменится. 529 – 435 = (529 – 5) – (435 + 5) =
524 – 440 = 84
16. Способ быстрого умножения.
Для получения единиц произведения перемножают единицы множителей, для
получения десятков умножают десятки одного на единицы другого множителя и
наоборот и результаты складывают, для получения сотен перемножают десятки.
62 * 58 = 3596
1) 8 * 2 = 16 (пишем 6, запоминаем 1)
2) 8 * 6 + 5 * 2 = 59 (пишем 9, помним 5)
3) 5 * 6 + 5 = 35
Изучив приёмы быстрого устного счёта, нам стало интересно, а известны ли
они школьникам. Учащимся пятого и десятого класса было предложено решить
устно четыре примера (умножение на 11, умножение двух двузначных чисел
близких к 100, умножение двух двузначных чисел близких к 10, возведение в
квадрат чисел оканчивающихся на 5) и ответить на ряд вопросов. Результаты опроса
представлены на диаграмме:
Результаты исследования
20
20
18
16
14
12
10
8
6
4
2
0
17
16
11
11
5 кл
3
2
всего
любят
устный счёт
думают, что
считают
быстро
3
приёмы
быстрого
счёта
известны
2
3
10 кл
справились
за 1 минуту
Чтобы доказать эффективность применения устного счёта, мы провели
эксперимент. Провели мастер-класс по приемам быстрого счёта и предложили
учащимся решить те же самые четыре примера. На диаграмме видно, что
применение приемов быстрого счёта эффективны, так как сокращают время,
затраченное на вычисления.
В наш век высоких технологий и повсеместного использования компьютера
умение быстро и правильно производить в уме достаточно сложные вычисления ни
в коем случае не утратило своей актуальности. Результаты опроса показали, что
большинство школьников не знакомы с приёмами быстрого устного счёта.
Старшеклассники для проведения расчётов предпочитают использовать
калькуляторы, хотя на ОГЭ и ЕГЭ они запрещены. Скорость устного счёта низкая,
поэтому практическая значимость данной работы велика. Помимо того, что
созданный сборник приёмов быстрого устного счёта могут использовать учителя на
уроках математики, физики учащиеся смогут и самостоятельного им
воспользоваться для тренировок на скорость устного счёта.
Для популяризации приёмов быстрого устного счёта планируется размножить
созданный сборник и распространить среди учащихся, а также проведение мастерклассов по теме «Быстрый счёт без калькулятора: правда или миф…»
1.
2.
3.
4.
5.
6.
7.
8.
Библиографический список
Бантова М. А. Система формирования вычислительных навыков. //Нач. шк —
1993.-№ 11.-с. 38-43.
Белошистая А. В. Приём формирования устных вычислительных умений в
пределах 100 // Начальная школа. — 2001.- № 7
Волкова СИ., Моро М. И. Сложение и вычитание многозначных чисел. //Нач.
шк.- 1998.-№ 8.-с.46-50
Демидова Т. Е., Тонких А. П. Приёмы рациональных вычислений в начальном
курсе математики // Начальная школа. — 2002. — № 2. — С. 94-103.
Мартынов И. И. Устный счёт для школьника, что гаммы для музыканта. //
Начальная школа. — 2003. — № 10. — С. 59-61.
Творогов В. Б. Наглядная арифметика и технология быстрого счёта. М.: Кн.1:
Основы. «Либроком», 2011. — 208 с. ISBN 978-5-397-01928-6.
Фаддейчева Т. И. Обучение устным вычислениям // Начальная школа. —
2003. — № 10.
Устный счёт. Режим доступа: https://ru.wikipedia.org/wiki/Устный_счёт.