Задачи: и отрезки касательных из точки к окружности с центром
реклама

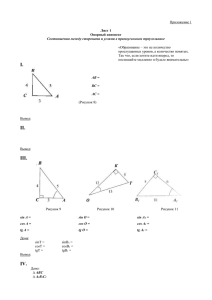
Задачи: а) 𝑆𝐴 и 𝑆𝐵 отрезки касательных из точки 𝑆 к окружности с центром 𝑂. Докажите равенство треугольников 𝐴𝑆𝑂 и 𝐵𝑆𝑂. б) Треугольники 𝐴𝐵𝐶 и 𝐾𝐿𝑀 вписаны в окружность. 𝐴𝐶 = 𝐾𝑀. Докажите равенство углов 𝐴𝐵𝐶 и 𝐾𝐿𝑀. в) Доказать, что прямые 𝑎 и 𝑏 параллельны. (Рисунок 2.7) a 120° b 60° Рисунок 1 г) 𝐴𝐻 – высота в равнобедренной трапеции 𝐴𝐵𝐶𝐷 (𝐴𝐷 = 𝐵𝐶). Найдите длину отрезка 𝐵𝐻, если 𝐴𝐷 = 2, 𝐵𝐶 = 6. д) В прямоугольном треугольнике длины гипотенузы и катета соответственно равны 5 и 2. Найдите длину другого катета. е) В прямоугольном треугольнике длины катетов равны 3 и 2. Найдите длину гипотенузы. ж) Найдите радиус описанной окружности около ∆𝐴𝐵𝐶, если 𝐴𝐵 = 6, ∠𝐶 = 30°. з) 𝐴𝑀 и 𝐵𝐾 – высоты треугольника 𝐴𝐵𝐶. 𝐴𝐶 = 6, 𝐵𝐶 = 7, 𝐴𝑀 = 5. Найдите длину 𝐵𝐾. и) На сторонах 𝐵𝐶 и 𝐴𝐶 треугольника 𝐴𝐵𝐶 лежат точки 𝐾 и 𝐿 соответственно. 𝐾𝐿 ∥ 𝐴𝐶, 𝐴𝐶 = 5, 𝐾𝐿 = 2, 𝐵𝐾 = 3, найдите длину 𝐵𝐶. Проверка: а) 𝑆𝐴 и 𝑆𝐵 отрезки касательных из точки 𝑆 к окружности с центром 𝑂. Докажите равенство треугольников 𝐴𝑆𝑂 и 𝐵𝑆𝑂. (Рисунок 2.8) Доказательство: 𝑆 𝐴 𝐵 𝑂 Рисунок 2 𝑆𝐴 = 𝑆𝐵 (как отрезки касательных), 𝐴𝑂 = 𝐵𝑂 (как радиусы), 𝑆𝑂 – общая сторона. Следовательно, треугольники 𝐴𝑆𝑂 и 𝐵𝑆𝑂 равны по трем сторонам. б) Треугольники 𝐴𝐵𝐶 и 𝐾𝐿𝑀 вписаны в окружность. 𝐴𝐶 = 𝐾𝑀. Докажите равенство углов 𝐴𝐵𝐶 и 𝐾𝐿𝑀. (Рисунок 2.9) Доказательство: 𝐿 𝐵 𝐾 𝐶 𝑀 𝐴 Рисунок 3 По условию хорды 𝐴𝐶 = 𝐾𝑀, а значит равны и дуги 𝐴𝐶 и 𝐾𝑀. Следовательно, углы 𝐴𝐵𝐶 и 𝐾𝐿𝑀 равны как вписанные, опирающиеся на равные дуги. в) Доказать, что прямые 𝑎 и 𝑏 параллельны. (Рисунок 2.10) a 120° b 60° Рисунок 4 Доказательство: Угол смежный с углом, равным 60°, равен 180°-60°=120°. Прямые 𝑎 и 𝑏 параллельны, так как при пересечении их секущей соответственные углы равны. г) 𝐴𝐻 – высота в равнобедренной трапеции 𝐴𝐵𝐶𝐷 (𝐴𝐷 = 𝐵𝐶). Найдите длину отрезка 𝐵𝐻, если 𝐴𝐷 = 2, 𝐵𝐶 = 6. (Рисунок 2.11) Решение: 𝐴 𝐵 𝐷 𝐻 𝐶 Рисунок 5 𝐵𝐶 − 𝐴𝐷 6 − 2 = = 2. 2 2 д) В прямоугольном треугольнике длины гипотенузы и катета соответственно 𝐵𝐻 = равны 5 и 2. Найдите длину другого катета. Решение: Обозначим длину искомого катета 𝑎. По теореме Пифагора 𝑎2 + 22 = 52 . Откуда 𝑎 = √21. а) В прямоугольном треугольнике длины катетов равны 3 и 2. Найдите длину гипотенузы. Решение: Обозначим длину гипотенузы 𝑐. По теореме Пифагора 𝑐 2 = 22 + 32 . Откуда 𝑐 = √13. ж) Найдите радиус описанной окружности около ∆𝐴𝐵𝐶, если 𝐴𝐵 = 6, ∠𝐶 = 30°. Решение: 𝑎 𝑏 𝑐 𝐴𝐵 По теореме синусов sin 𝛼 = sin 𝛽 = sin 𝛾 = 2 ∙ 𝑅. Следовательно, 𝑅 = 2∙sin ∠𝐶 = з) 6 2∙ 1 2 = 6. 𝐴𝑀 и 𝐵𝐾 – высоты треугольника 𝐴𝐵𝐶. 𝐴𝐶 = 6, 𝐵𝐶 = 7, 𝐴𝑀 = 5. Найдите длину 𝐵𝐾. Решение: 1 1 Воспользуемся методом площадей. 2 ∙ 𝐴𝑀 ∙ 𝐵𝐶 = 2 ∙ 𝐴𝐶 ∙ 𝐵𝐾. 𝐵𝐾 = 𝐴𝑀∙𝐵𝐶 𝐴𝐶 = 5∙7 6 = 35 6 . и) На сторонах 𝐵𝐶 и 𝐴𝐶 треугольника 𝐴𝐵𝐶 лежат точки 𝐾 и 𝐿 соответственно. 𝐾𝐿 ∥ 𝐴𝐶, 𝐴𝐶 = 5, 𝐾𝐿 = 2, 𝐵𝐾 = 3, найдите длину 𝐵𝐶. (Рисунок 2.12) Решение: 𝐵 𝐾 𝐿 𝐴 𝐶 Рисунок 6 ∆𝐴𝐵𝐶 ∾ ∆𝐿𝐵𝐾 с коэффициентом подобия равным отсюда 𝐵𝐶 3 5 = 2, 𝐵𝐶 = 15 2 . 𝐴𝐶 𝐾𝐿 5 𝐵𝐶 2 𝐵𝐾 = . Следовательно, 5 = , 2